一种基于均匀稀疏采样的Lamb波场重构方法
2019-09-24
(江苏大学 国家级高端装备关键结构健康管理国际联合研究中心,镇江 212013)
Lamb波传播距离远,能量衰减小,检测范围大,且对结构内部缺陷敏感,在板状结构的无损检测与评估中有着广泛应用[1-2]。传统的Lamb波检测方法常利用分布式传感器阵列拾取波场信号以定位损伤,但此类方法具有以下缺点:① 传感器需通过耦合剂与试件黏接,采样信号易受耦合剂影响;② 阵列排布形式固定,操作不灵活;③ 空间分辨率受限,难以针对损伤的尺度、形状等特征作精确评估[3]。使用非接触式扫描激光多普勒测振仪(Scanning Laser Doppler Vibrometer,SLDV)能够获得板状结构被测区域内高空间分辨率Lamb波场数据,并利用波场分析技术对损伤进行精确评估[4-6]。“波场”主要指行波在被测结构的研究区域中传播,与结构特征相互作用产生的一系列随时间演化的图像。在采集波场数据的过程中,受限于Nyquist采样定律,空间采样间隔必须小于最小半波长,因此测点数量庞大;且对单个测点需多次测量取均值以提高信噪比。密集扫描形成海量数据不仅耗时,且给数据的存储、传输及分析带来巨大挑战。
近年来有学者利用压缩感知(Compressive Sensing,CS)技术框架,通过随机采样策略在采样率远低于Nyquist采样率的条件下采集波场的空间离散样本点信号,然后采用非线性重建算法恢复波场[7-8]。如:LEVINE等采用稀疏分布式传感器阵列拾取波场信号,通过压缩感知方法实现了金属板中多个缺陷的定位,然而该方法需在试件表面布置大量压电传感器,且无法获得高分辨率波场,从而难以提取更多关于损伤的量化信息;ESFANDABADI等[8]在IANNI等[9]的研究基础上利用不同稀疏基精确重构波场,并根据其差异实现了对缺陷的检测;基于稀疏重构算法和SLDV采样,MESNIL等[10]对含损铝板和复合材料板进行损伤成像和波场重构,并与试验测量所得的高空间分辨率波场进行了对比。ESFANDABADI与MESNIL提出的损伤检测方法均可通过少量空间测点信号精准重构出波场,并能实现损伤的高精度定位和成像,但两者均依赖随机采样策略,需在现有的商用SLDV系统上增加额外的控制组件,进而增加了系统的复杂度和成本。
笔者使用一种新的采样策略,用等间距的均匀稀疏采样网格替代随机的空间测点坐标,同时随机选定假定源的位置,重新构建波场稀疏重构框架,利用SLDV测得的含损铝板试验数据对提出的方法进行了验证。构建的基于SLDV均匀稀疏采样的波场重构方案可高效获取研究区域内的Lamb波场数据,对于提高基于波场分析的损伤检测技术的效率具有重要意义。
1 Lamb波场稀疏重构框架
1.1 压缩感知理论简介
经典的Nyquist-Shanon采样定理认为,为了不失真地恢复模拟信号,采样频率要高于模拟信号频谱的最高频率的两倍,但该定理仅利用了信号带宽有限的假设,并未利用到其他关于信号的先验知识。DONOHO[11]等提出了一种全新的信号欠采样和恢复理论,即压缩感知理论。该理论充分利用了原始信号在某组预先设定的基础上可以稀疏表达的先验信息,通过随机投影在远低于Nyquist频率的采样频率下对信号进行压缩采集,然后将得到的少量测量值输入到一个优化求解器中恢复出原始信号。
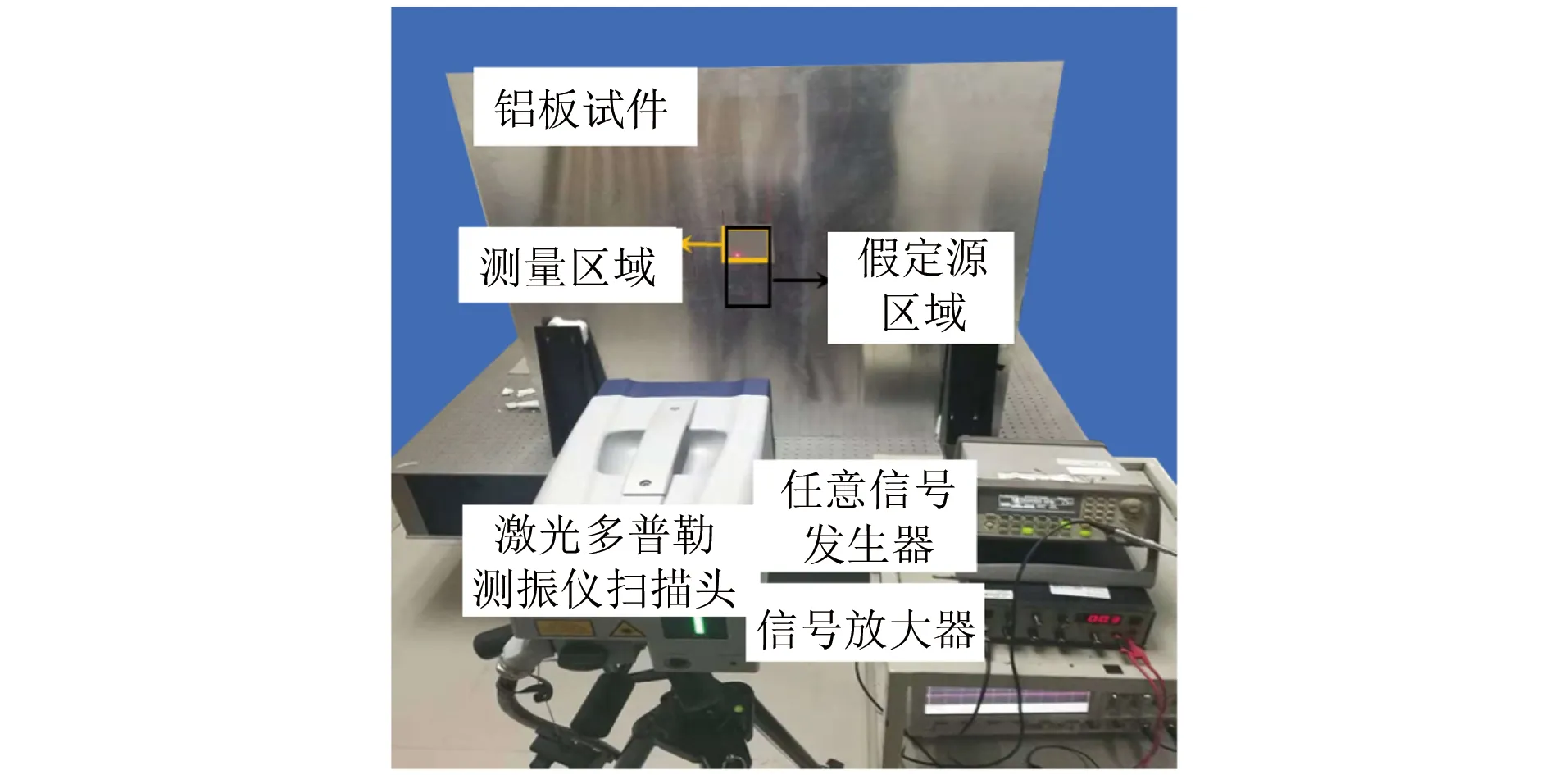
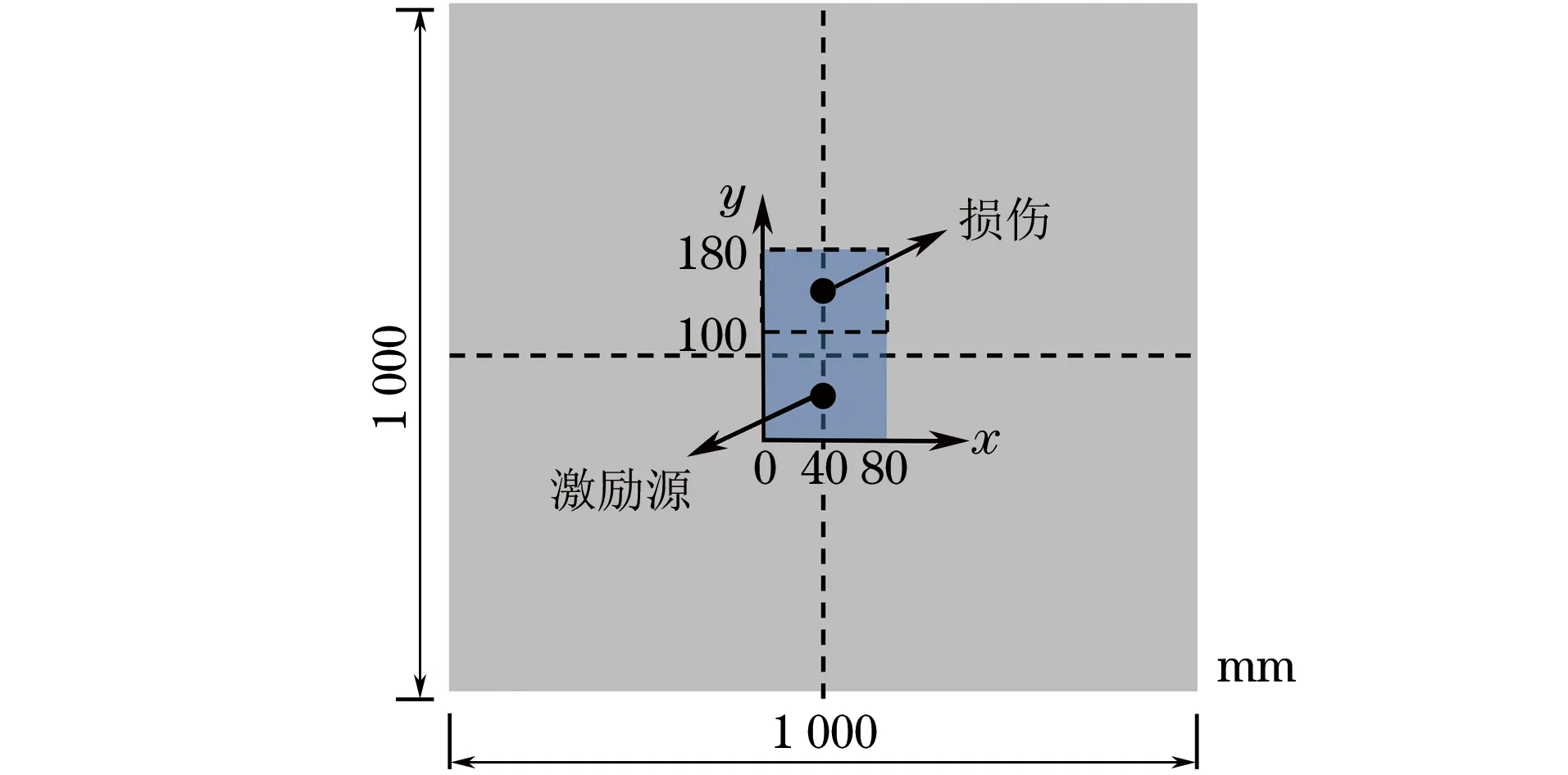
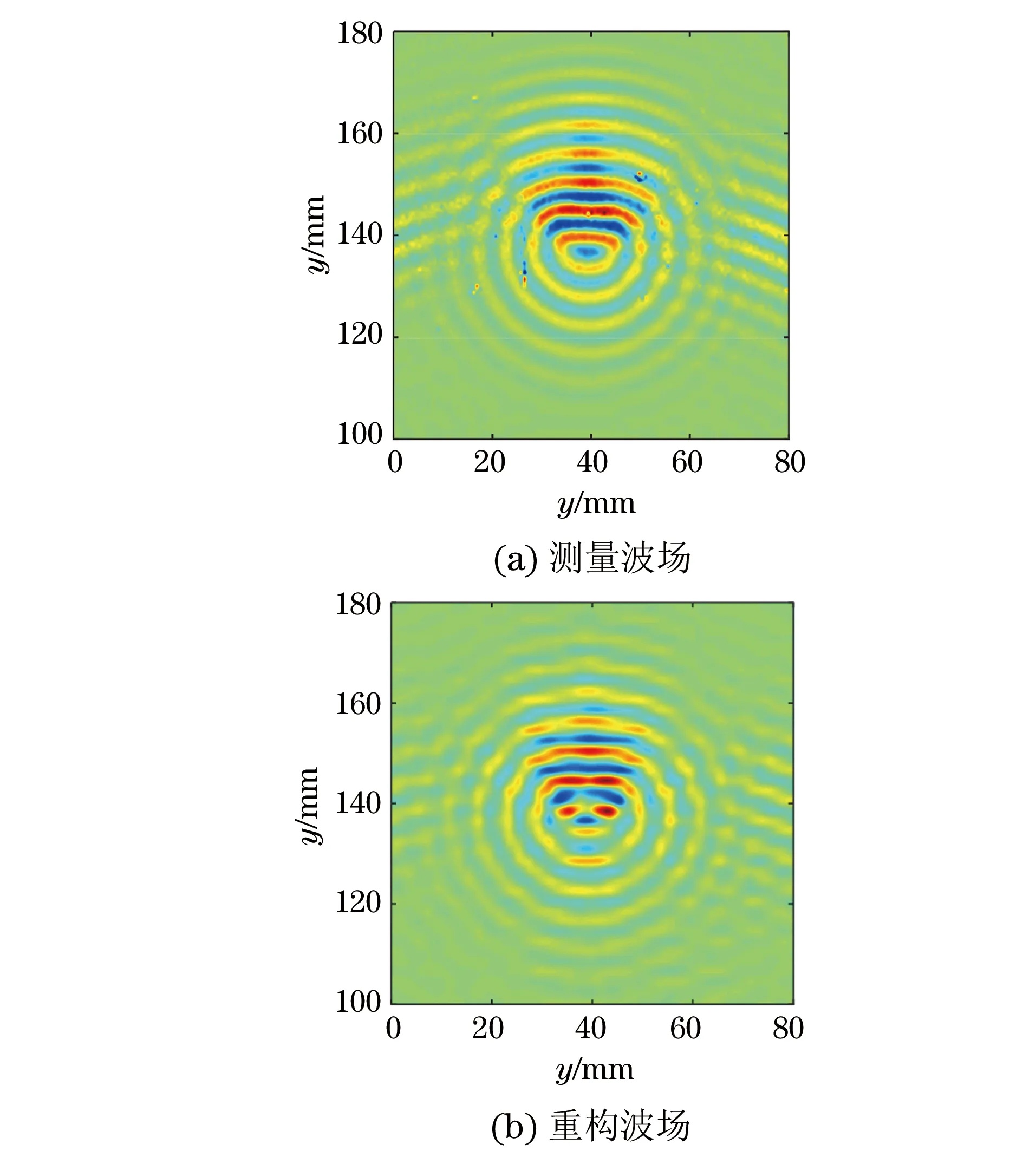
压缩感知问题在数学上可描述如下:设一维信号x∈RN×1的稀疏度为K,即x中仅含K个非零值;观测矩阵Φ∈CM×N,且M 使用SLDV在试件表面拾取Lamb波场时,通常需要设置大量的采样点,其中属于结构特征(如激励源、损伤、预留孔洞和边界等)的点非常有限,因此可结合导波的传播机理与结构特征的稀疏性构建波场压缩感知方程,通过求解方程来估计结构特征的位置,并重构出完整Lamb波场。 将待测结构表面检测区域等间距地划分为N个像素点,则在这些像素点中,位于结构特征附近的像素点个数通常是有限的。将这N个像素点视作“假定源”,而将位于结构特征附近的像素点视作真实的“源”,即能够主动激励或散射导波的结构特征所覆盖的点,显然真实源的存在具有相当高的稀疏性,因此可依据源的稀疏性构造压缩感知方程,并通过求解方程找到真实源的位置。 设假定源编号为s(s=1,2,…,N),测量点编号为m(m=1,2,…,M),且M (1) 通过理论计算进行估计,由于在各向同性板中,能量主要以几何形式扩散,所以仅考虑几何衰减,忽略材料耗散等因素。当考虑所有测点信号时,式(1)可改写为 y(μ)(f)=Α(μ)(f)v(μ)(f) (2) (3) (4) (5) 理论上,在多模态情况下仍可用相同的方式构造压缩感知方程,但为了计算方便,采用较低的激励频率,使得激励源仅产生A0与S0模态,此时式(2)扩展为 y(f)=Α(A0)(f)v(A0)(f)+Α(S0)(f)v(S0)(f)= Α(f)v(f) (6) 即得到最终的压缩感知方程(以下简称“CS方程”),其中Α(f)为传感矩阵。 为使传递矩阵满足约束等距性质(RIP),在采样过程中必须兼顾均匀性和随机性。有文献通过抖动采样[13]生成稀疏采样点,并将假定源坐标设为等间距网格点,网格间距取最小波长的一半,如图1(a)所示。商用SLDV测量系统内置的测量网格为均匀网格,为使SLDV稀疏采样更易实现,笔者将随机的测点坐标替换为等间隔均匀采样网格坐标,同时用抖动采样方法生成假定源坐标,如图1(b)所示,这样既便于使用SLDV系统对测点坐标进行设置,又可保证压缩感知对传递矩阵的随机性要求。 图1 两种采样点与假定源点坐标设置示意 确定采样点坐标后,利用SLDV采集信号,将测量信号的频谱代入压缩感知框架,通过基追踪降噪算法求解下述问题 (7) 式中:ε(f)为与信号噪声水平相关的常量。 求得假定源激励函数后,选定波场重构区域,构造假定源到该区域Nyquist采样点之间的传递矩阵Α′,可得该区域Nyquist采样点频谱W(f) W(f)=Α′(f)v(f) (8) 然后对W(f)作逆傅里叶变换,得到任意时刻全波场数据W(t)。设定的波场重构区域与测量区域重合,此处需注意的是,波场的重构区域理论上可任意选择,但在远离检测区域的位置处的信号的重构精度将有所降低。为了评估波场重构效果,采用重构波场与原始波场的相干系数来衡量波场的重构精度。 通过假定源激励函数的幅值信息可直接进行损伤定位和成像。由于在激励频率与SLDV测量环境下,A0模态导波成分在测量信号中占主导地位,所以利用v(f)中A0模态部分的幅值信息进行损伤成像,成像指标index(x,y)的计算方法为 (9) 式中:index(x,y)为点(x,y)处的假定源成像指标;f1,f2分别为计算频段的起止频率。 图2 PZT激励/SLDV传感平台外观 构建如图2所示的PZT激励/SLDV传感试验平台。待测试件为6061型号铝板,尺寸(长×宽×高)为1 000 mm×1 000 mm×1 mm。在铝板表面建立二维笛卡尔坐标系(见图3),激励源为直径为7 mm的压电片,其坐标为(40,40),在(40,145)处黏贴另一直径为7 mm的压电片以模拟损伤。图3中的蓝色区域为假定源区域,宽80 mm,高180 mm;虚线框为稀疏测量区域,宽高均为80 mm,在测量区域内每个采样点上采集10次数据取平均值,以提高信噪比。激励信号选择中心频率为250 kHz的五峰波,图4为激励信号的时域、频谱图。从图4(b)可看出,激励信号的能量主要集中在100 kHz400 kHz内,因此选择该区间作为计算频带。通过试件的频散曲线数据,可推算得到计算频段内波场最小波长约为4.68 mm,因此假定源区域的Nyquist采样点数为2 695。在假定源区域选取N个点作为假定源,并在测量区域均匀稀疏采样M个点的信号值,定义采样压缩率SC=(1-M/N)×100%,在实际测量中,取N=2 695,M=221,采样压缩率SC=91.8%。在试验中稀疏测量时间为63 s,比在假定源区域全测量减少768 s。 图3 待测铝板坐标系示意 图4 激励信号的时域图与频谱图 所使用的原始试验信号为减去无损参考信号后的残余信号,图5(a)为利用SLDV密集采样得到的残余波场在62.3 μs时刻的截图,从该图可观察到,激励源产生的波场仍有残余部分,在损伤后方残余激励源波场强度非常高。理论上可通过假定源的激励函数重构出任意区域的波场,将波场重构区域与假定源区域一致。图5(b)为从重构波场中截取得到的损伤周围区域波场(即重构出的波场在62.3 μs时刻的截图)。从波场重构的直观结果可以看出,重构波场与测量波场具有较高的一致性。图6为在点(20,140)处的测量信号与重构信号对比图,可见重构信号与测量信号相位匹配较好。 图5 62.3 μs时刻的测量波场与重构波场 图6 点(20,140)处的重构信号与测量信号 计算得到的损伤成像结果如图7(a)所示,其中图7(a)为归一化成像指标的二维平面分布,图7(b)为其三维分布。由图7(b)得到的损伤中心位置为(38.8,146.7),与损伤中心真实位置相差2.1 mm,在误差波场最小半波长的一半以内,说明该方法定位较为准确。图8为重构波场与测量波场在各频率段的相干系数曲线,从图中可以看出,在计算频段内大部分频率对应的重构系数在0.95以上,重构系数最高值可达0.99,说明所提出的方法可较为精确地重构出原始波场。 图7 损伤成像结果 图8 重构波场与测量波场在各频率段的相干系数曲线 通过稀疏重构的方法获取波场可显著减少测量时间,但重构计算量较大,其耗时也是影响检测效率的重要因素之一。求解CS方程在总体计算过程中占主导地位,其求解时间与方程规模相关。CS方程的规模主要与测点数量M、假定源数量N及常数ε(f)等有关,通过研究不难发现,CS方程计算耗时与以上3个因素均为线性关系。在研究区域确定后,依据Nyquist定律即可确定假定源数量N的最小值;根据试验研究可知,在M达到测量区域内Nyquist采样点数的90%左右时,即可获取高精度的重构波场;而常数ε(f)可根据试验结果进行选取。虽然重构过程增加了后续的计算量,但计算过程一般在数秒内即可完成,而测量完整波场信号比稀疏采样需多消耗数十分钟到几个小时的时间,因此通过稀疏采样无疑可以极大地提高检测效率。 通过试验数据验证了利用均匀稀疏采样方案重构Lamb波场的可行性和重构效果,并利用假定源激励函数的幅值信息对损伤进行定位和成像。结果表明,所提出的方法可极大地提高研究区域Lamb波场的获取效率,同时重构出的波场在计算频段内与原波场具有较高的一致性,损伤定位的误差可控制在波场最小波长的一半以内。1.2 Lamb波场压缩感知方程的构建
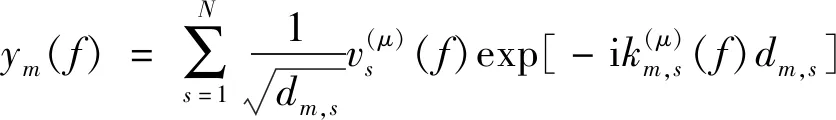


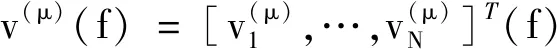





1.3 波场重构与损伤成像

2 试验验证
2.1 试验设置

2.2 波场重构结果

2.3 损伤成像与重构效果评价


3 结语
