黏接结构弱黏接缺陷的非线性超声评价

陈 军，乔 丹，崔 哲2，马海涛

(1.大连理工大学 材料科学与工程学院，大连 116024;2.大连理工大学 鞍山研究院，鞍山 114051)

黏接结构是一种利用黏接剂将金属与金属、金属与非金属或非金属与非金属黏接起来的结构，具有比模量高、结构质量小和连接应力分散等特点，广泛应用于航空航天、车辆制造、建筑等领域[1]。黏接过程中工艺变量的微小差异会使黏接结构产生缺陷，如胶接剂在使用过程中分布不均匀，会在黏接界面上形成弱黏接、空隙和脱粘等缺陷，这些缺陷的存在会破坏黏接结构的完整性，对其使役性能造成重大影响[2]，因此需要采用有效的无损检测手段来评价黏接界面品质，以保证黏接结构的安全服役。

目前，对于黏接结构的无损检测有很多种方法，如超声、射线、红外和微波等。其中射线检测的周期长、费用高，不适合大面积检测；红外检测技术对温度的要求比较高，缺陷定性困难、缺陷尺寸定量精度不高[3]；微波不能检测以金属或碳纤维等导电材料为外层的复合结构的内部缺陷；而超声检测由于穿透能力强、灵敏度高、检测速度快，且适用范围广而被广泛使用[4]。常规的超声检测使用反射或透射超声波的幅值变化或相位变化来表征材料损伤，对材料或结构内部存在的分层、裂纹或孔洞等宏观缺陷比较敏感，而对于微小缺陷的检测具有一定的局限性[5]。与其相比，非线性超声检测则是利用在材料内部传播的超声波与介质或微小缺陷相互作用产生的非线性响应信号来评估结构性能和检测微小缺陷的，对黏接结构的黏接强度退化、弱黏接、微裂纹等特性的变化更为敏感[6]。

AZ31镁铝合金因强度高、塑性好、质量小、耐磨性好、衰减性能好等良好的综合性能被广泛应用于汽车、航空和航天等行业[7]，笔者选择AZ31镁铝合金为待黏接试件、环氧树脂E-44为胶黏剂、聚乙烯薄片为缺陷来制作黏接结构试样，采用模拟和试验的方法对含有不同弱黏接面积的AZ31黏接试样进行非线性表征。

1 非线性超声理论基础

由于黏接结构界面的性能变化与非线性效应密切相关，所以可利用脉冲超声波在黏接结构材料中传播时产生的非线性特征来评价黏接结构的黏接质量[8]。该方法将超声波与接触界面相互作用的宏观特性与接触表面的微观特性联系起来，可以用来检测材料内部，如弱黏接等缺陷[9]。黏接结构中的弱黏接和黏接界面都可能导致单频或窄带入射波的畸变，从而导致谐波的产生，这些非线性效应导致应力σ和应变ε之间的关系不再满足胡克定律，需引入高阶弹性项[10]

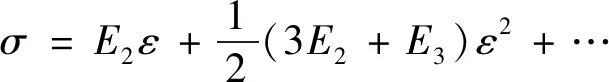
(1)

式中：E2和E3分别是二阶和三阶弹性系数。

固体介质内一维非线性波动方程[11]为

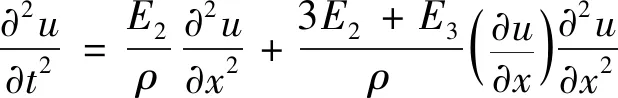
(2)

式中：ρ为介质密度；t为传播时间；x为传播距离。

在黏接结构中，由部分接触的黏接界面而导致的应力-应变行为中的非线性同样会引起单一频率的超声波或者窄带入射超声波发生畸变，这被称为接触声学非线性机制[12]。假设入射初始声波方程为

u(0,t)=A1sinωt

(3)

式中：A1为基波幅值;w为角频率。

使用逐级近似微扰法，可得非线性波动方程的近似解为

u(x,t)=A1sin(ωt-kx)+

(4)

式中：k为波数;β为二阶非线性系数。

由式(4)可知，二次谐波幅值为

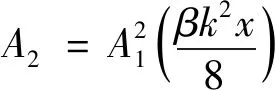
(5)

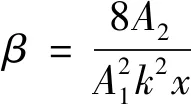
(6)

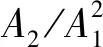
(7)

因此可以通过测量基波幅值A1和二次谐波幅值A2来确定材料的相对非线性系数β′。

2 模拟方法和结果

2.1 建模及参数选择

根据非线性超声理论，利用ABAQUS有限元软件建立黏接结构的非线性超声检测有限元模型。AZ31镁铝合金试样的黏接长度为50 mm，宽为20 mm，厚度为8 mm，超声波沿试件厚度方向激励和接收。建立50 mm×8 mm的二维平面单元，黏接结构的有限元模型如图1所示。边界条件设置为自由边界，材料参数如表1所示。

图1 黏接结构有限元模型

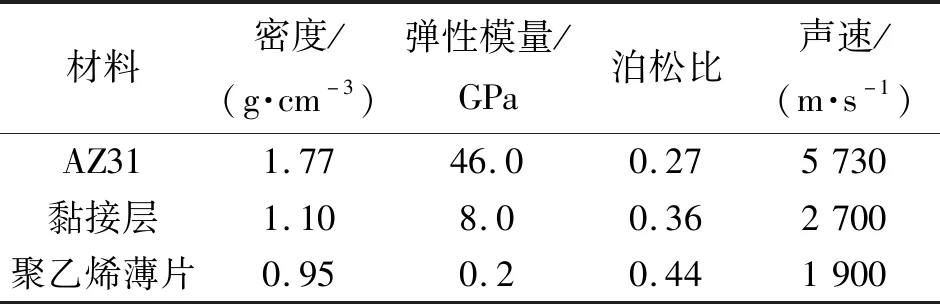
表1 模型中的各材料参数

选择经Hanning窗调制的单频正弦脉冲串作为激励信号，调制后信号的瞬时位移载荷为

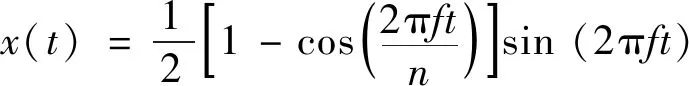
(8)

式中：f为激励信号的频率，选择f=5 MHz；n为脉冲串个数，超声波传播过程中，脉冲串的个数越多，非线性效应累积越明显。

为了确保发射脉冲串与回波不发生重叠，脉冲宽度不能超过接收到回波的时间为

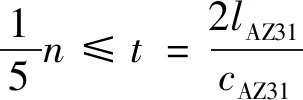
(9)

式中：cAZ31为超声波在AZ31镁铝合金中传播时的纵波声速；lAZ31为被黏接试件的厚度。

经计算n≤6.98，因此选择n=6。将f和n代入式(8)中，得到激励信号的时域波形如图2所示。

通常有限元模型中的网格单元尺寸小于波长的十分之一，模型中λAZ31=1.146 mm，λ黏接层=0.54 mm。因此，为了减少计算量，选择AZ31镁铝合金层的网格尺寸为0.1 mm，黏接层的网格尺寸为0.05 mm。划分网格的有限元模型如图3所示。

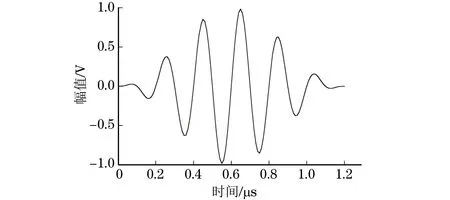
图2 激励信号时域波形

图3 划分网格的有限元模型

2.2 模拟结果

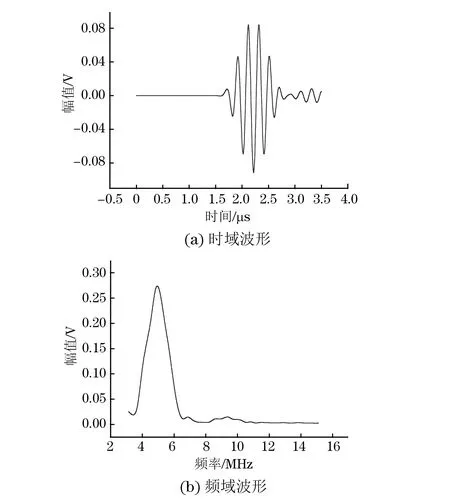
图4 无缺陷时接收信号的时域波形和频域波形

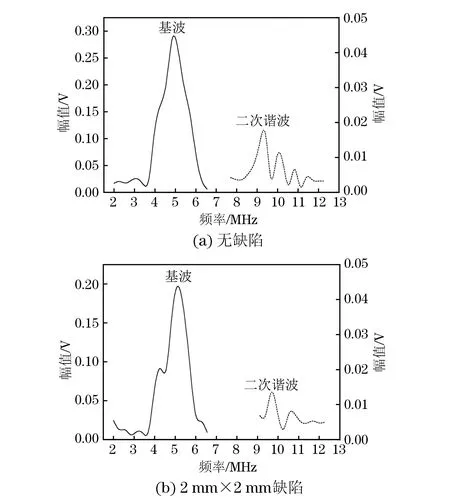
图5 无缺陷和缺陷尺寸为2 mm×2 mm时接收信号的频域波形

依次对含有尺寸(长×宽)为2 mm×2 mm，4 mm×4 mm，6 mm×6 mm，8 mm×8 mm的弱黏接缺陷模型进行模拟计算，无缺陷时接收信号的时域波形和频域波形如图4所示。有缺陷时接收信号波形发生变化，图5(a)和5(b)分别是无缺陷和缺陷尺寸为2 mm×2 mm时接收信号的频域波形，可以发现基波幅值和二次谐波幅值都发生了明显变化，根据式(7)计算不同尺寸缺陷的相对非线性系数β′，计算结果见表2，相对非线性系数随缺陷尺寸的变化曲线如图6所示。从图6和表2可以看出，随着缺陷尺寸的增大，基波和二次谐波的幅值逐渐减小，而非线性系数却逐渐增大。由于缺陷尺寸的增大，透射声波的能量越来越小，故基波和二次谐波幅值呈逐渐减小的趋势；但由于非线性效应的增加，二次谐波幅值的下降比基波幅值下降得慢，导致非线性系数随着缺陷尺寸的增大呈现逐渐增大的趋势。表明超声非线性系数对黏接结构试样中弱黏接缺陷尺寸的变化非常敏感。

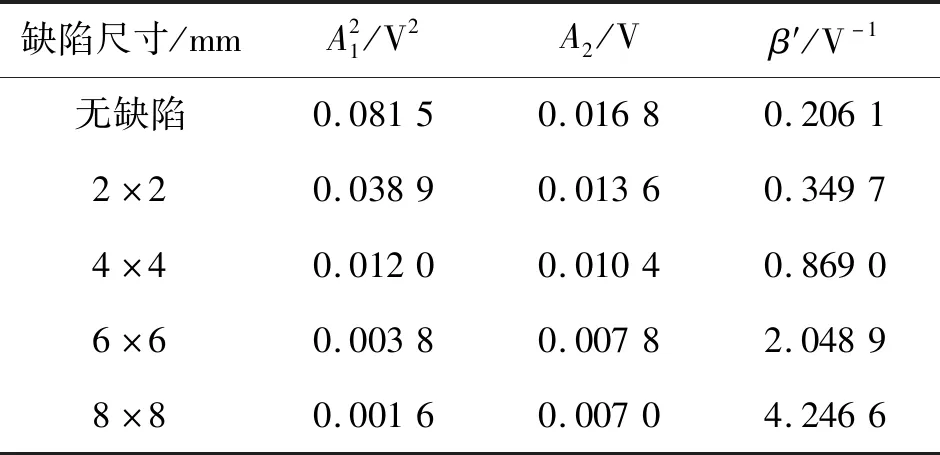
表2 接收信号幅值和相对非线性系数计算结果

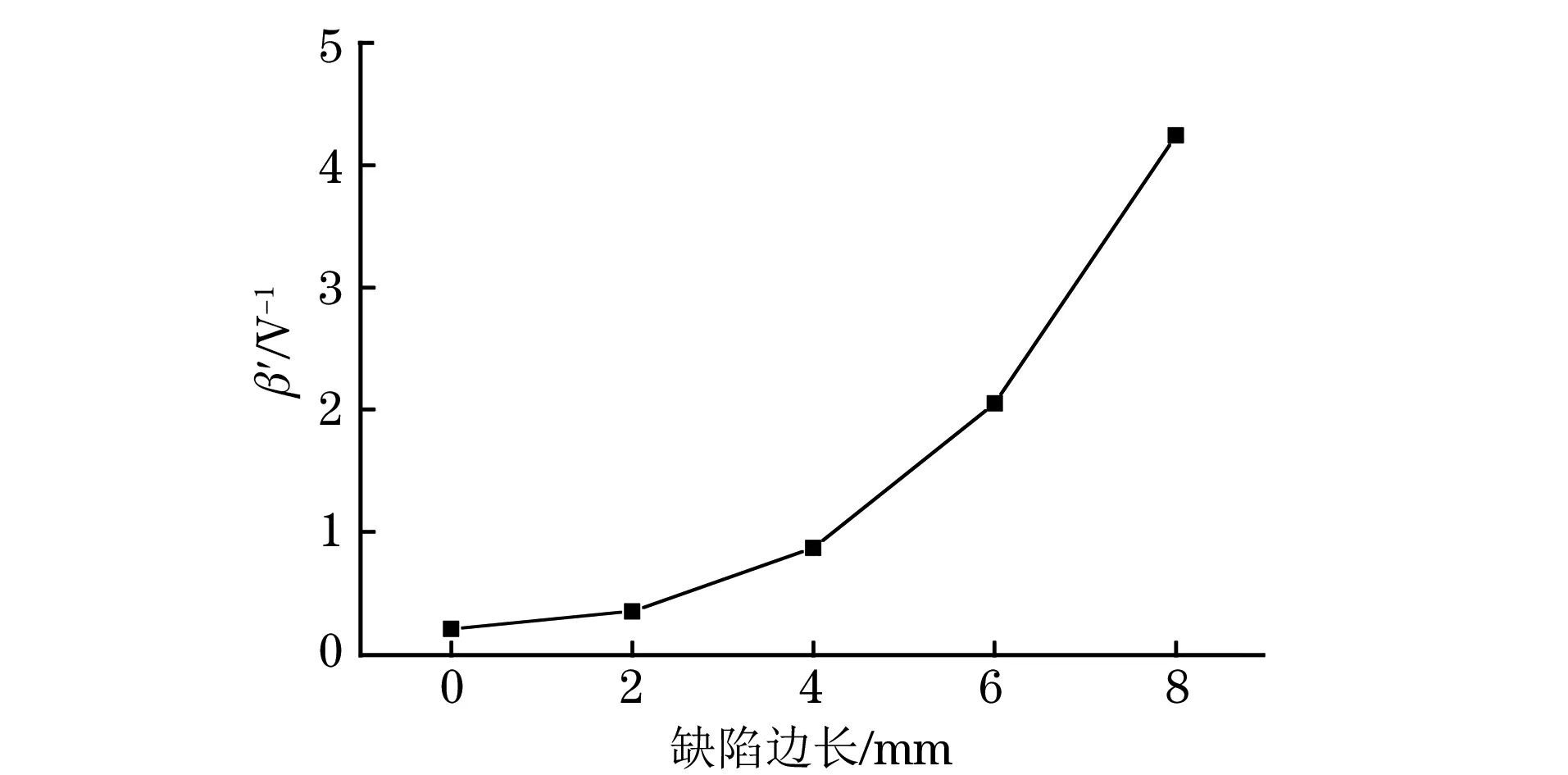
图6 相对非线性系数随缺陷尺寸的变化曲线

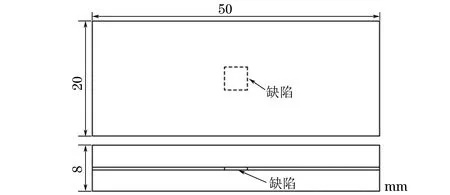
图7 试样尺寸示意

3 试验过程

3.1 试样制备

试样尺寸示意如图7所示。在试样切割完成后，使用粒度为400的砂纸轻微打磨试样表面，然后用无水乙醇擦拭待黏接试样的连接部分，清洁试样黏接面的杂质。在制作黏接结构试样时，预先埋入尺寸分别为2 mm×2 mm，4 mm×4 mm，6 mm×6 mm，8 mm×8 mm的聚乙烯薄片作为弱黏接缺陷，将配置好的胶黏剂放置在40℃左右的温水上，不断搅拌至没有气泡后均匀涂抹于试样连接处，然后按压试样黏接处使其平面保持平整，保证几个试样的厚度基本一致，最后将黏接试样放置24 h后，即可作为检测试样使用。

3.2 非线性系数的测量

采用脉冲透射法来测量非线性系数，测试系统为美国Ritec公司生产的RAM-5000-SNAP非线性超声测试系统(见图8)。RAM系统能够通过门式放大器来增强入射波的振幅，发射单一频率的正弦脉冲串。试验中的激励信号所用的频率和脉冲串个数与模拟中的一样，分别是5 MHz和6。为了保证发射信号的波形不发生畸变，选择衰减为13 dB，输出电压为30 V。示波器的采样频率为1 GHz·s-1，接收探头的中心频率为10 MHz。无缺陷时接收信号的时域波形和频域波形如图9所示。有缺陷时接收信号的波形发生了变化，图10分别是无缺陷和缺陷尺寸为2 mm×2 mm时基波与二次谐波信号的幅频特性曲线。根据式(7)来计算不同弱黏接面积的黏接结构试样的相对非线性系数。

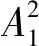
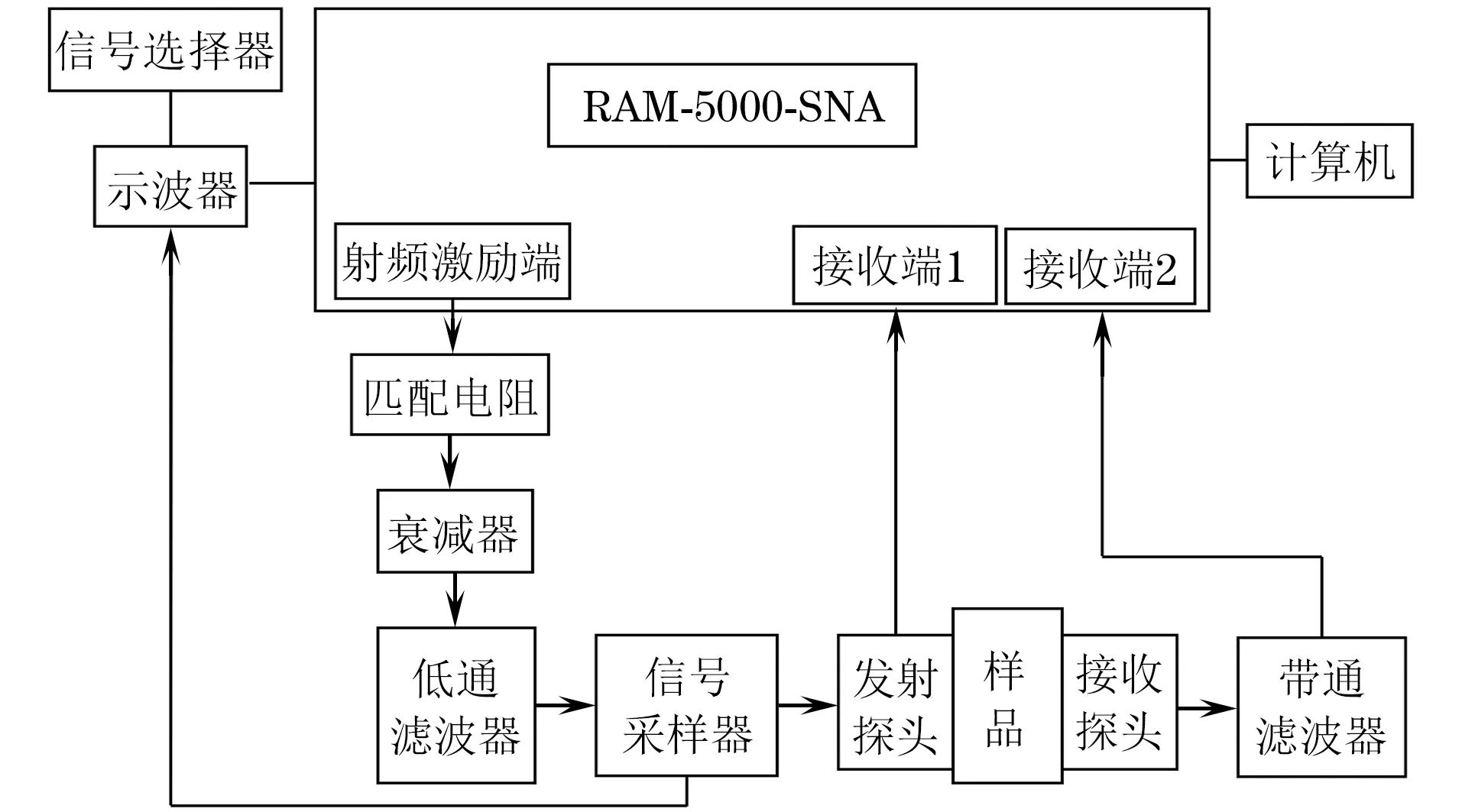
图8 非线性超声测试系统框图

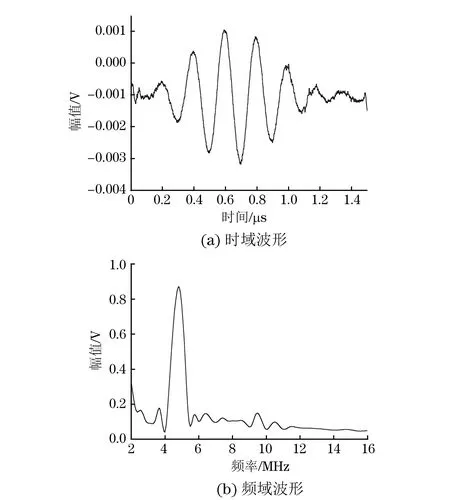
图9 无缺陷时接收信号的时域波形和频域波形

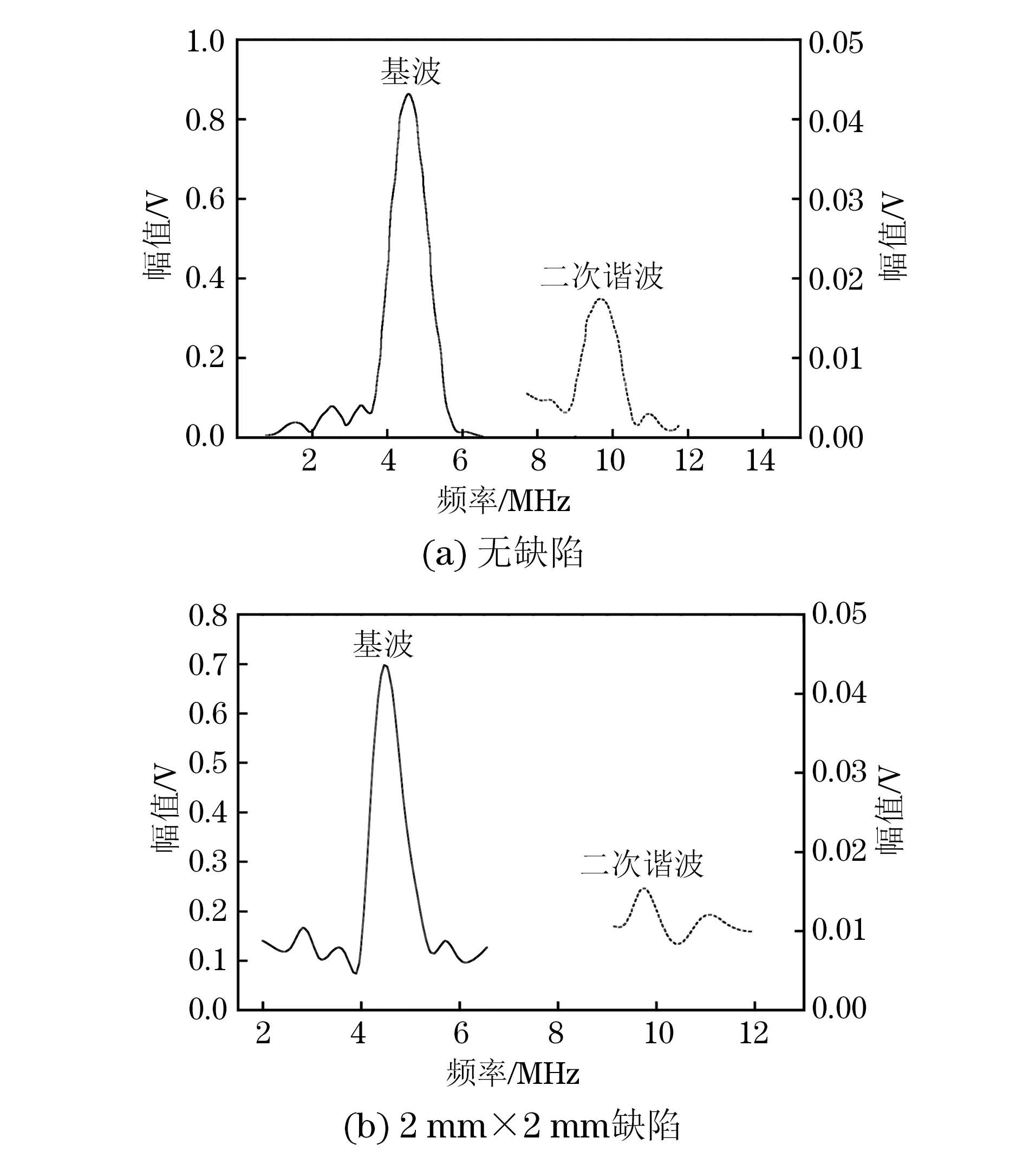
图10 无缺陷和缺陷尺寸为2 mm×2 mm时接收信号的幅频特性曲线

图与A2的关系曲线

3.3 试验结果

接收信号幅值及相对非线性系数测量结果如表3所示，表3中数据是经过10次测量得到的平均值，相对非线性系数与弱黏接面积的关系曲线如图12所示。

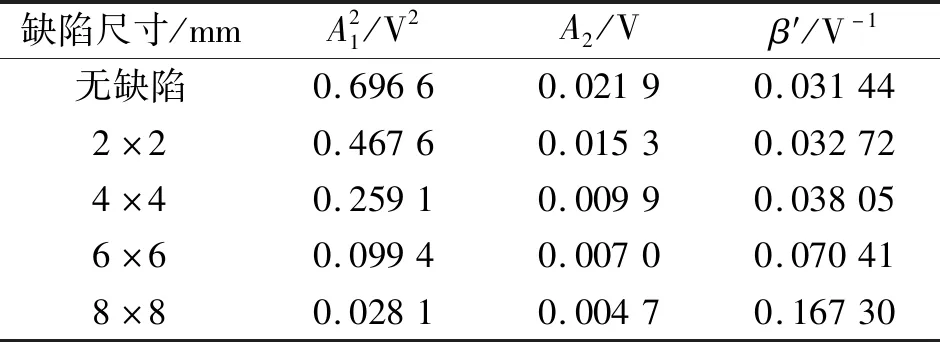
表3 接收信号幅值及相对非线性系数测量结果

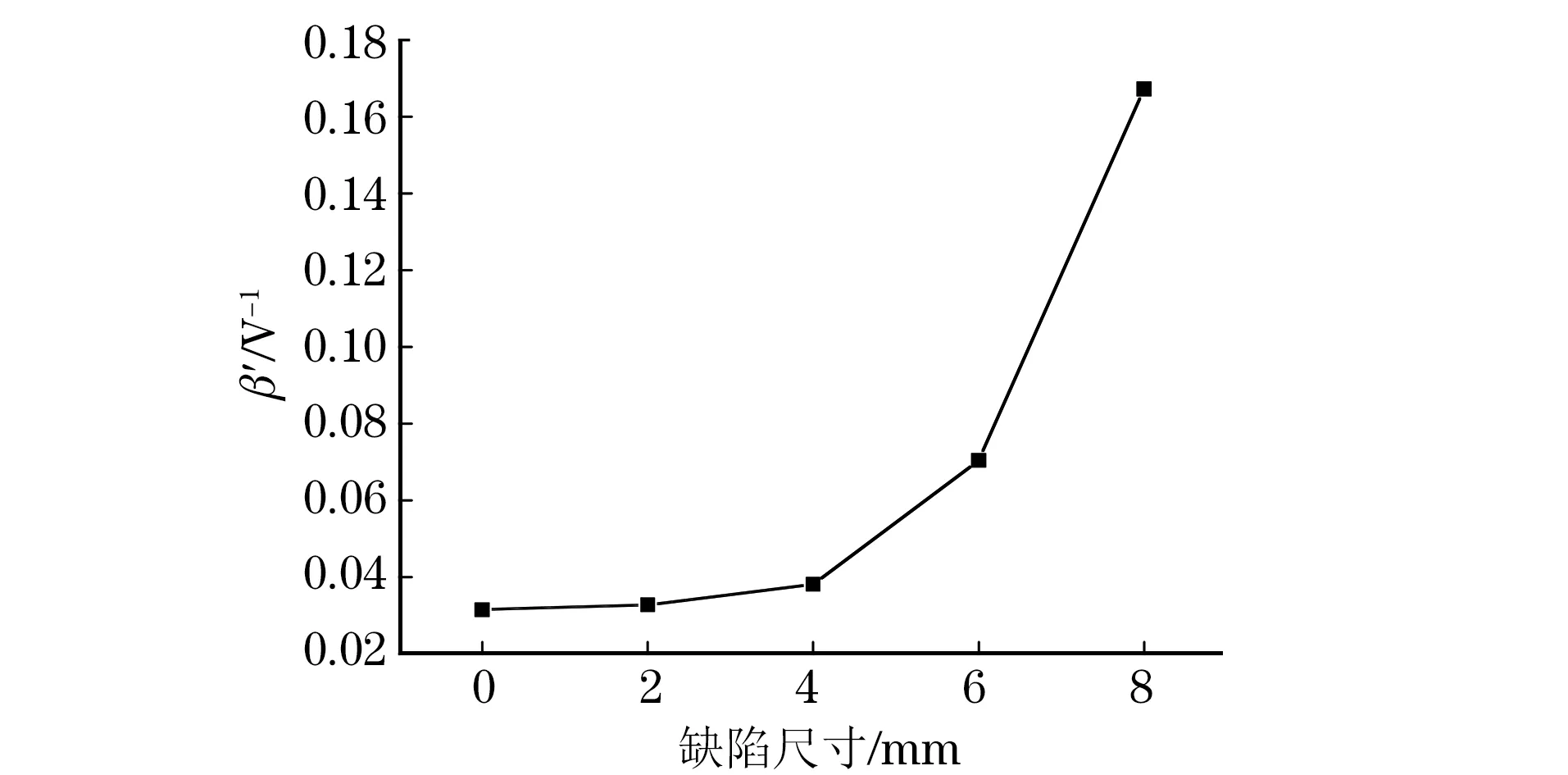
图12 相对非线性系数与弱黏接面积的关系曲线

从表3中的数据变化可以看出，随着弱黏接面积的增加，基波和二次谐波幅值都不断减小。这是因为当入射超声波遇到脱黏界面时，界面两侧材料的声阻抗差异较大，接收到超声波信号的能量减少，随着弱黏接面积的增大，接收到信号的能量变弱，接收信号基波和二次谐波的幅值越来越小。

从图12可以看出,随着弱黏接面积的增大，相对非线性系数逐渐增大。超声波传播过程中的非线性来源主要分为经典非线性和接触非线性:前者主要与材料晶格的非简谐性有关，是材料的固有属性；后者主要与材料内部裂纹、接触面或者界面的应力-应变非线性有关。通过对响应信号频谱分析可知，完好黏接部位信号频谱中的非线性系数较小，这部分的非线性与材料经典非线性有关，是材料晶格非简谐性所致。当黏接界面含有缺陷时，超声回波信号的非线性系数变大，而且随着脱黏面积的增大非线性效应增加得更快。

4 结语

通过对黏接结构试样中的弱黏接缺陷进行非线性超声检测和ABAQUS有限元模拟，发现随着弱黏接缺陷尺寸的增大，基波和二次谐波幅值呈现逐渐减小的趋势，而相对非线性系数则逐渐增大，而且非线性系数的相对变化量约是基波幅值相对变化量的5.4倍，表明了非线性超声检测在黏接结构质量检测方面的有效性。利用非线性超声检测可以检测出黏接结构中的弱黏接缺陷，为黏接结构黏接界面缺陷的定性、定量检测奠定了基础，也为多层黏接结构界面黏接质量评价提供了指导意义。