带涂层圆柱形零件表面缺陷的激光超声特性

(大连理工大学 机械工程学院，大连 116024)

圆柱形零件是工业中常用的承力部件，其表面通常有涂层加以保护。在进行表面缺陷的超声检测时，往往需要去除表面涂层,去除涂层将增加检测的工作量，显著降低检测效率，甚至会对零件表面造成损伤[1-3]。激光超声技术是近年来兴起的一项无损检测技术，其具有非接触、无损伤、时间和空间分辨率高等优点。利用激光激发出超声表面波信号对金属表面缺陷进行快速有效检测，在圆柱形零件的无损检测中逐渐受到关注。

目前，激光超声在无涂层圆柱形零件表面的传播规律已有较多的研究，并取得了一系列的研究成果[4-6]。ZHAO等[7]研究了在金属铝圆柱表面裂纹宽度和深度与激光超声表面波反射信号之间的关系；许伯强[8]通过有限元法模拟了层状材料中传播的时域信号，并且利用神经网络对层状材料参数进行了反演；曹建树，CAVUTO[9-10]等基于工程实际试验研究了激光超声表面波在石油管道、列车车轴等圆柱形金属零件表面裂纹的检测。但是，对于带涂层圆柱形零件表面缺陷检测的研究还少有报道。显然，为了提高带涂层圆柱形零件表面缺陷的检测效率，研究激光超声沿零件表面的传播特性是一个非常重要的课题。

笔者利用有限元方法建立了线状脉冲激光作用在带涂层金属圆柱形零件表面时表面超声波的数值模型，分析了涂层对声表面波时频域信号的影响，研究了在铝基底镍涂层下金属圆柱形零件表面时频域信号与涂层厚度、裂纹深度之间的关系，为激光超声用于带涂层圆柱形零件表面缺陷的检测提供参考。

1 带涂层圆柱形零件表面缺陷检测模型

1.1 数值模型的建立

脉冲线源激光经透镜聚焦后沿圆柱母线方向垂直辐照在带涂层圆柱形金属零件外表面上，所研究的为沿圆周方向传播的超声表面波，简化的二维物理模型如图1所示。图1中,d为圆柱的直径，h为圆柱外表面涂层的厚度，hw与hc分别为人工矩形缺陷的宽度与深度，φ为缺陷与激光激发点之间的角度，θ为观测角。

数值计算中采用空间上均匀分布，时间上呈高斯分布的线状激光光源，将其转换为热流密度加载在圆柱表面。在激光辐照区域[-α，α]内等效的热流密度Q为

Q(r,φ,t)|-α≤φ≤α=I0Af(r)g(t)

(1)

式中：A为介质对激光的吸收率；I0为激光峰值功率密度；f(r)和g(t)分别为脉冲激光的空间和时间分布。

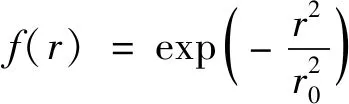
(2)

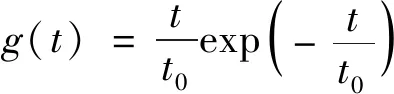
(3)

式中：r0为激光光斑半径；t0为激光脉冲宽度。

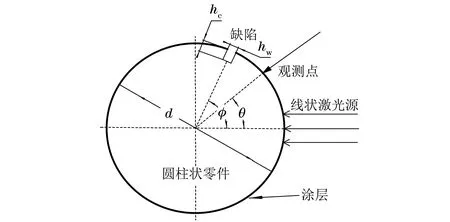
图1 线状激光源作用模型

1.2 激光和材料有关参数

基于上述物理模型，采用有限元软件ANSYS Mechanical APDL建立了激光线源热-结构耦合模型。仿真过程考虑材料内部的热传导，忽略材料与外界的热对流、热辐射。激光超声的产生过程包括瞬态温度场和位移场两个过程，因为结构场求解结果对温度场的影响很小，因此采用顺序耦合方式，即先求解出温度场分布，然后将温度场作为载荷再进行位移场求解。

利用有限元数值模拟了直径d为12 mm的带镍涂层金属铝圆柱形零件表面激发的超声表面波，取单脉冲激光能量为13.5 mJ，脉冲上升时间为10 ns，激光光斑半径为300 mm，介质表面吸收率为0.07。圆柱形零件基底和涂层金属材料的主要热物理参数如表1所示。

表1 基底与涂层材料的主要热物理参数(温度为300 K时)

2 涂层对圆柱形零件中声表面波的影响

2.1 涂层对声表面波时频域信号的影响

为了研究涂层对声表面波信号的影响，分别建立了不同涂层厚度的有限元模型，当涂层厚度h为0，200，400，600 mm，观测角θ为60°时，所得到的时域波形如图2所示。从图2可以看出，在不带涂层时所得到的为典型的表面波，由掠面纵波sP，表面横波sS和双极性表面波R组成，如图2(a)所示。当存在不同厚度的涂层时，瑞利波的到达时间相比无涂层的滞后，即当涂层存在时，其中产生了色散，如图2(b)和图2(c)所示。

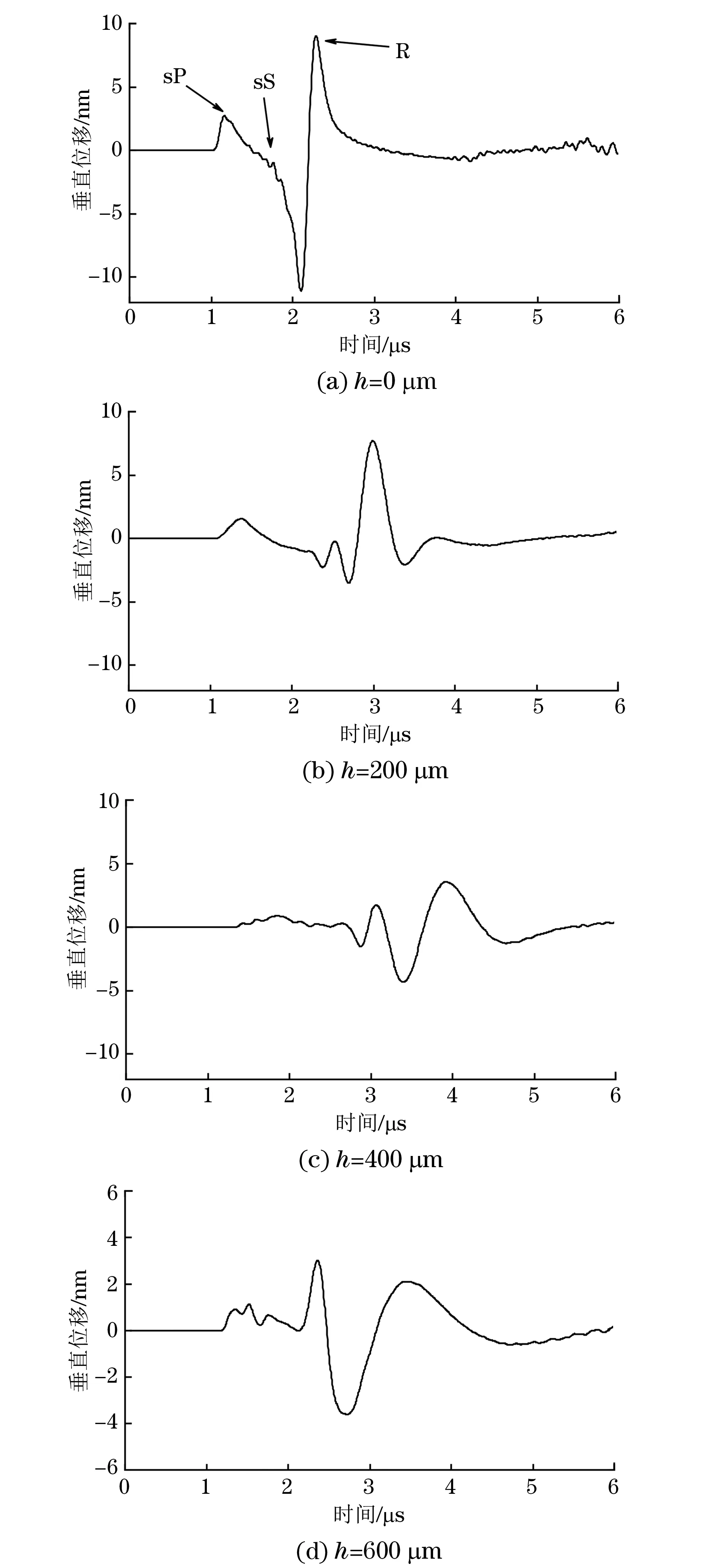
图2 不同涂层厚度零件的声表面波时域波形

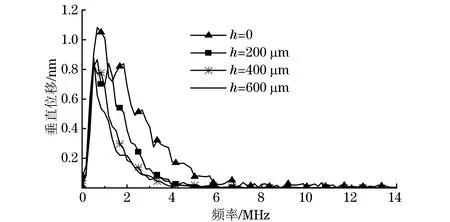
图3 不同涂层厚度零件的声表面波频域波形

这是因为表面瑞利波中的低频成分波长较长，会穿透涂层进入铝基底中传播；高频成分的波长较短，因此集中在表面涂层中传播。由图3频域波形可以看出，与无涂层时域信号相比，有涂层时信号高频成分减少，说明有涂层时部分低频成分的表面瑞利波穿透涂层进入铝基底中传播，另一部分在镍涂层中传播，而低频成分比高频成分传播得快，所以高低频成分发生了分离，产生了色散。当涂层厚度增加到一定程度时，色散现象又开始减弱，形成类似单一介质中的典型表面波波形，如图2(d)所示。

2.2 涂层对表面瑞利波波速的影响

涂层的存在，会使声表面波产生色散，对表面瑞利波波速也存在影响。涂层厚度h为0～500 mm时，根据瑞利波R的到达时间计算出表面瑞利波的波速，并对曲线进行拟合，结果如图4所示。由图4可以看出，表面瑞利波波速随着涂层厚度的增加，先从基底中的速度开始逐渐减小至最小，然后增大至涂层材料中的传播速度。这是因为在一定的涂层厚度下，表面瑞利波会在涂层与基底的界面传播，此时由于两种不同介质之间的反射而表面瑞利波会产生较大的衰减，速度逐渐降为最小，而随着涂层厚度的增加，表面瑞利波将集中在涂层中，以涂层中的速度传播。

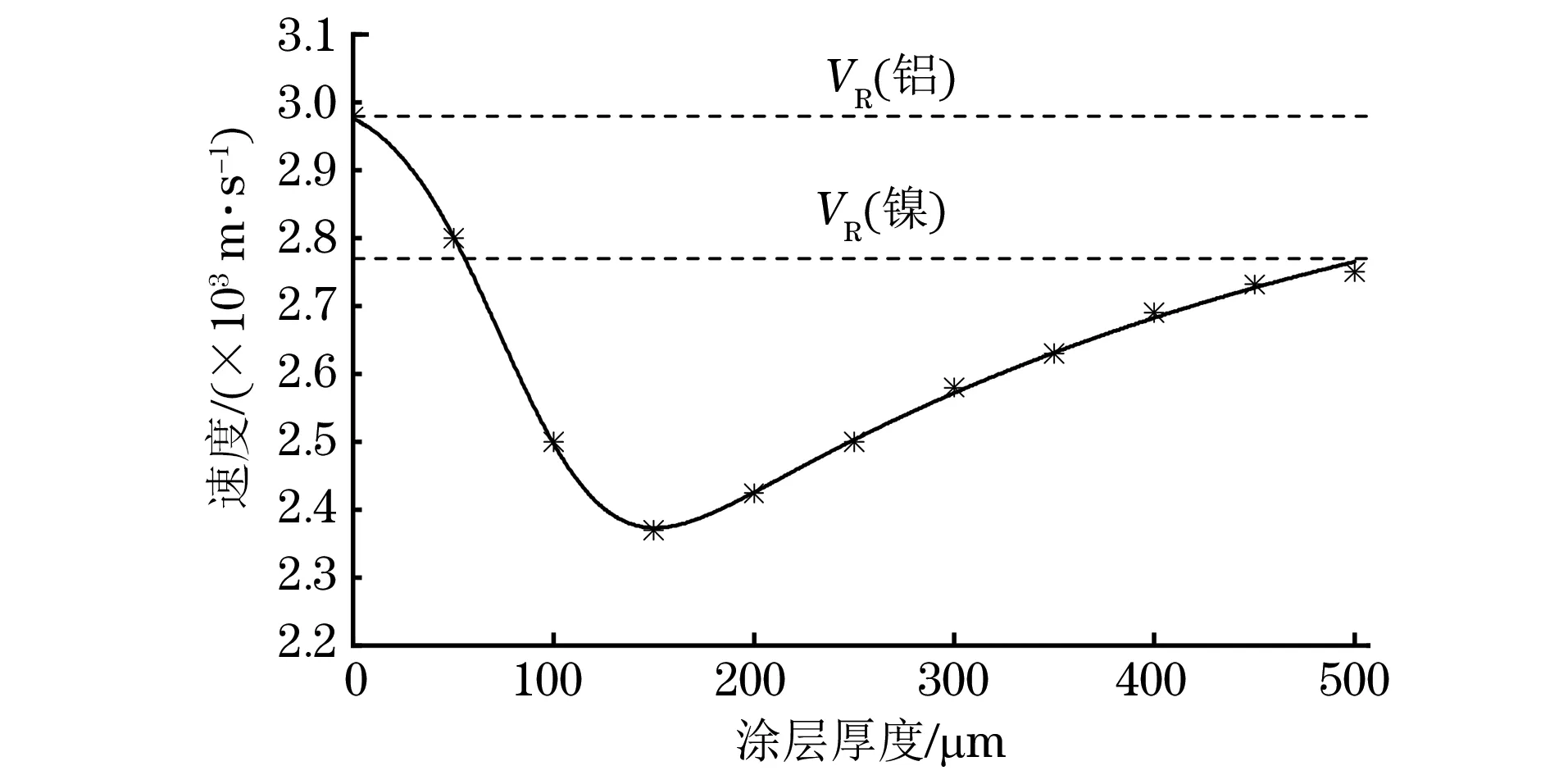
图4 不同涂层厚度下的瑞利波波速曲线

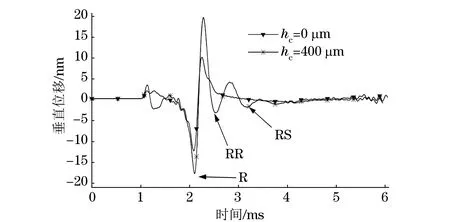
图5 缺陷深度为0.3 mm、观测角为30°时的声表面波时域波形

3 激光超声与缺陷相互作用分析

3.1 反射信号与缺陷深度之间的关系

图5为缺陷位置φ为90°，缺陷深度hc分别为0 mm(无缺陷)与400 mm时得到的声表面波信号时域波形。从图5可以看出，当有缺陷存在时，反射信号中出现了明显的特征波峰RR与RS。这与刘辉等[11]在半无限大平面结构中的研究规律相似，RR与RS是由于缺陷的存在引起的，RR是缺陷左边界形成的反射，RS是缺陷的底端形成的反射。RR与RS波峰的存在为柱状材料中表面裂纹的检测提供了依据。

计算RR与RS波的到达时间差，可以发现RR波与RS波的到达时间差t与缺陷的深度之间存在着关系。计算不同涂层厚度下RR波与RS波的时间差t与缺陷深度的关系，结果如图6所示。从图6可以看出，在不带涂层时，RR与RS时间差t与缺陷深度之间近似成线性关系；涂层厚度为200 mm和400 mm时，t与缺陷深度之间近似成分段线性关系，分界点大致在缺陷深度与涂层厚度相等处。

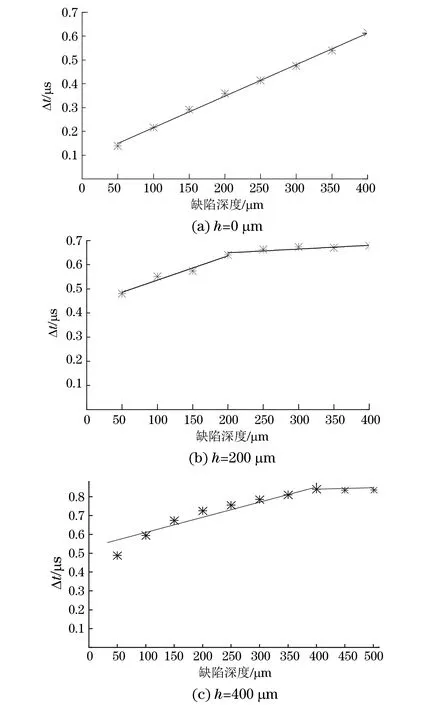
图6 不同涂层厚度下，RR波与RS波的时间差与缺陷深度之间的关系

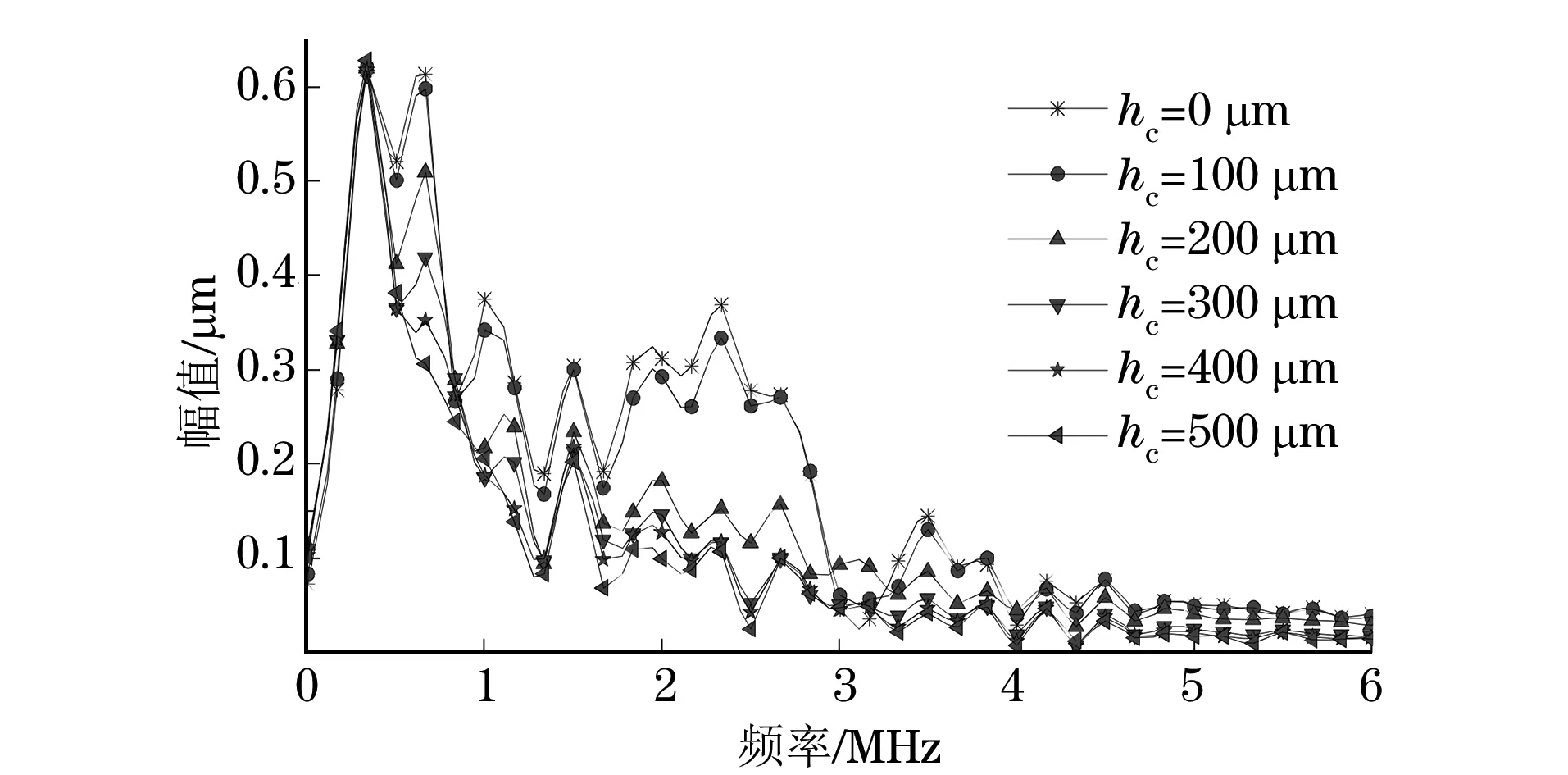
图7 涂层厚度为200 mm时，透射波信号的FFT变换结果

3.2 透射信号与缺陷深度之间的关系

图7为涂层厚度为200 mm时，透射波信号的快速傅里叶变换(FFT)结果，从图7可以看出，随着缺陷深度的增加，表面波频域信号低频成分和高频成分的幅值均不断减小，如0.8 MHz和2.4 MHz频率成分，并且在缺陷深度小于涂层厚度时的幅值明显大于较大涂层厚度下的。这表明，在带涂层时缺陷仍然对表面波信号存在着选频作用，通过透射信号波中心频率的幅值大小也能够对表面缺陷的大小提供参考。

4 结论

基于有限元法对带涂层圆柱形零件表面的激光超声特性进行了研究，分析了带涂层表面缺陷深度与反射和透射信号之间的关系。研究发现：涂层厚度在200，400 mm时，在金属铝基底镍涂层材料中产生了明显色散现象。涂层厚度进一步增加到600 mm时，色散现象减弱，形成了类似单一介质中的表面波信号；涂层厚度分别为0,200,400 mm时，圆柱表面瑞利波反射信号中产生特征波峰RR与RS，并且时间差Δt与缺陷深度之间存在着分阶段线性关系，分界点大致为缺陷深度与涂层厚度相等处；透射波频域信号的幅值随着缺陷深度的增加而减小，对缺陷深度存在着选频作用。数值研究的结果为带涂层圆柱形金属零件和其他弯曲表面裂纹的激光超声检测提供了依据。