基于宕渣路基的沥青路面结构力学性能研究

(1.沈阳建筑大学交通工程学院， 辽宁沈阳110168；2.大连海事大学交通运输工程学院, 辽宁大连116000;3.浙江大学交通工程研究所， 浙江杭州3100580)

0 引言

我国道路建设行业在经济快速发展的大环境下已经取得长足发展，但是传统的路基填筑施工方式已经严重威胁了生态平衡，且现有的土类填筑材料难以满足道路建设行业长远发展的需求。将宕渣材料应用到路基填筑施工当中，不仅可以有效地避免大量农地被占用，也可以很好地解决施工过程中渣土对环境严重污染的问题，故越来越多的道路工程选择宕渣作为施工材料[1-3]。

宕渣作为一种建筑废料，力学性能良好，且便于取材[4-6]。研究表明，将宕渣材料用于路基填筑施工，可以减小路面设计厚度与路表弯沉Ls、明显增大路基的E0、缩减道路造价[7-9]。宕渣路基受到面层传递荷载与结构层自重的作用[10-11]。宕渣填筑路基可以直接影响到路面结构设计，但有关其对路面结构影响的研究较少，故借助有限元软件研究宕渣路基对沥青路面结构层的影响具有重要意义[12-13]。

为研究宕渣路基对沥青路面结构层力学性能的影响，通过ABAQUS软件分析了路面结构参数在宕渣填筑路基作用下的变化规律。结果表明，宕渣填筑路基，可以明显改善路面结构的力学性能，且具有较好的经济效益。

1 循环压缩试验

为获得宕渣路基回弹模量的取值范围，给ABAQUS平台的材料参数取值提供理论依据，本文以宕渣土石混合料为研究对象，开展了不同试验条件下的循环压缩试验。

1.1 试验用料与仪器

试验材料为宕渣土石混合料和水。选用仪器为JZ-ZD型电动重型击实仪和WDW-100型加载机，如图1和图2所示。

图1 击实仪
Fig.1 Compaction apparatus

图2 WDW-100型加载机
Fig.2 WDW-100 loading equipment

1.2 试验级配与含水率

试验采用文献[14-15]等量代换法求得的三种级配，如表1所示。三种级配分别选用如表2所示的五组含水率w开展试验[1]。

表1 试验级配Tab.1 Test gradation

图3 应力σ—应变ε曲线Fig.3 Stress-strain curves

1.3 试验过程

①选用尺寸为210 mm×125 mm×62 mm的大试盒,将重型击实后的试件取样放入大试盒中,并且保证每次取样的质量控制在1 000 g左右,计重后放入烘箱,按土工试验规程步骤操作最终测定级配1、2和3的最佳含水率分别为13.2 %、14 %、14.5 %。

②在级配1最佳含水率附近分别取5个预加含水率进行拌料和闷料,制备重型击实循环压缩试件。

③将循环压缩试件分别放在电子万能试验机上,使压头以速度v=1 mm/min竖直向下,控制试件受竖直方向的最大应力为1 MPa时卸载，待试件恢复形变,测其回弹变形量。

④以此将试件循环压缩20次,在电脑上采集试验数据,得到应力—应变曲线图,如图3所示。求得回弹模量后,分别测试5个试件的实际含水率。

⑤根据上文所述分别制备级配2和级配3的5个循环压缩试件,依次重复②～④的步骤。

1.4 回弹模量的确定

第n次压缩加载的回弹模量En的求解公式如式(6)所示，回弹模量E0的求解公式如式(7)所示，因为试件在第一次加载期间不稳定，故不考虑E1。求得的回弹模量如表2所示，由表2知，测得的宕渣土石混合料回弹模量为157.3～254.8 MPa。根据表2绘制回弹模量E0-含水率w曲线，如图4所示，由图4可知，含水率w对三种级配的回弹模量E0影响规律基本相同，且对级配2的回弹模量E0的影响最小。考虑到级配2对应的回弹模量E0受含水率w影响最小，故建议采用级配2的宕渣土石混合料作为路基填筑材料，取试验结果的平均值244 MPa作为工程建议值。使用式(8)对回弹模量E0—含水率w曲线进行拟合回归，拟合结果如表3所示，由表3可知，二次函数能较好地刻画w与宕渣土石混合料回弹模量E0之间的关系[1,9-10]。

(6)

(7)

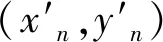
E0=-aw2-bw+c，

(8)

式中：w为含水率；a，b，c为拟合参数。

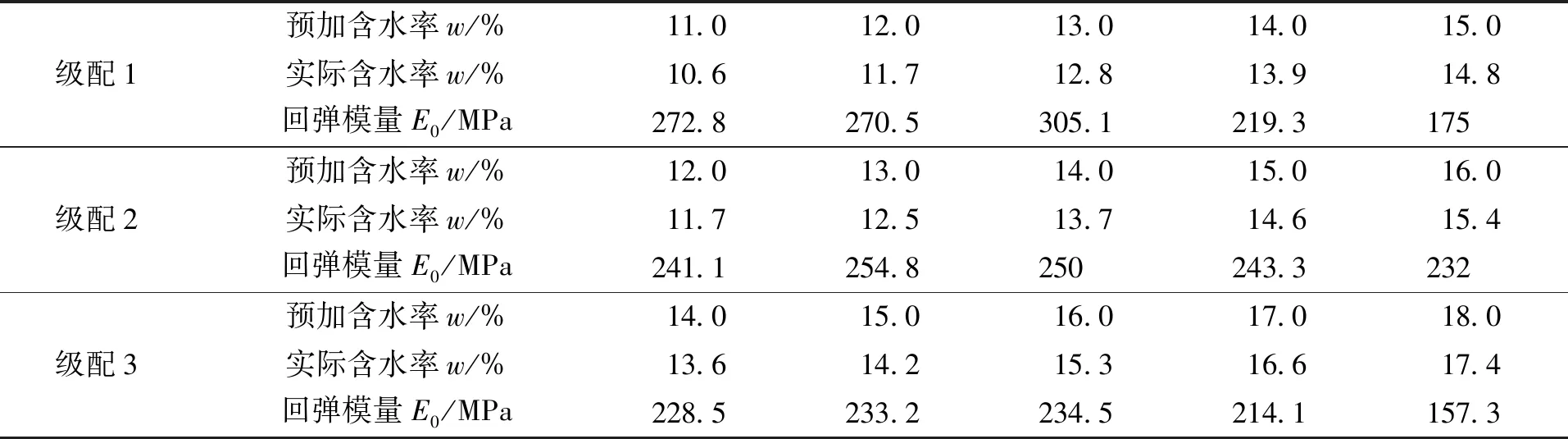
表2 回弹模量E0结果Tab.2 Results of resilient modulus

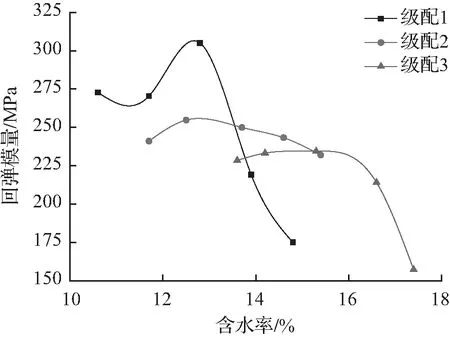
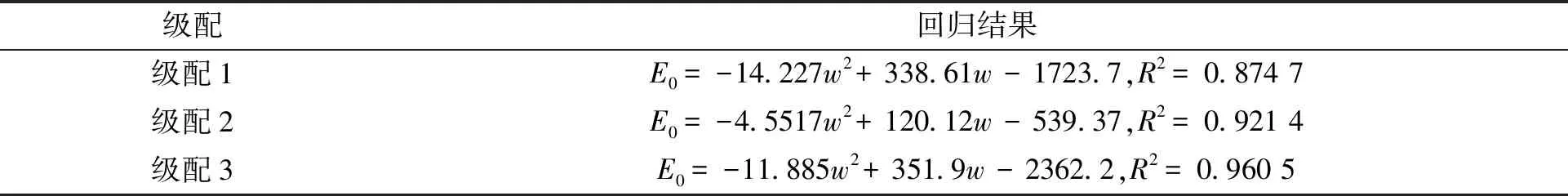
图4 回弹模量E0—含水率w曲线Fig.4 Resilient modulus-water content curves

2 宕渣路基对路面结构层的影响

2.1 建立路面结构三维模型

2.1.1 模型的建立

图5 网格划分图Fig.5 Mesh generation

通过ABAQUS软件分析不同宕渣路基E0对路面结构参数的影响。作用在路面的交通荷载一般为瞬时荷载且瞬时应力数量级较低，故将路面结构层视为线弹性体，路面各结构层材料假设为均匀弹性。路面荷载选择双圆均布荷载BZZ-100。将模型的空间尺寸为宽度4.375 m，深度2.74 m，长度5 m[16]。底部x、y、z三个方向的位移约束和转动约束均为0，左右两侧x方向位移约束、y和z方向转动约束为0。单元类型如图5所示。

2.1.2 选取路面结构和确定参数

根据循环压缩试验结果选取三组宕渣的回弹模量E0，分别：150 MPa、200 MPa、250 MPa。两种水泥质量分数分别为5 %和3 %的水稳碎石参数根据文献[17]进行取值，其余各个结构层参数按规范中值来赋值。路面结构参数如表4所示[18]。

表4 路面结构参数Tab.4 Parameters of pavement structure

2.2 模拟计算结果分析

路面结构参数结果如表5所示，根据表5绘制路基回弹模量E0与结构参数的关系图，如图6～图10所示，由图6～图10可知，E0取试验值150～250 MPa时，E0与上述参数关系曲线走势为平缓。在宕渣材料处在最不利饱水状态时，其路面结构参数结果优于土基路面结构参数结果。计算结果具体分析如下。

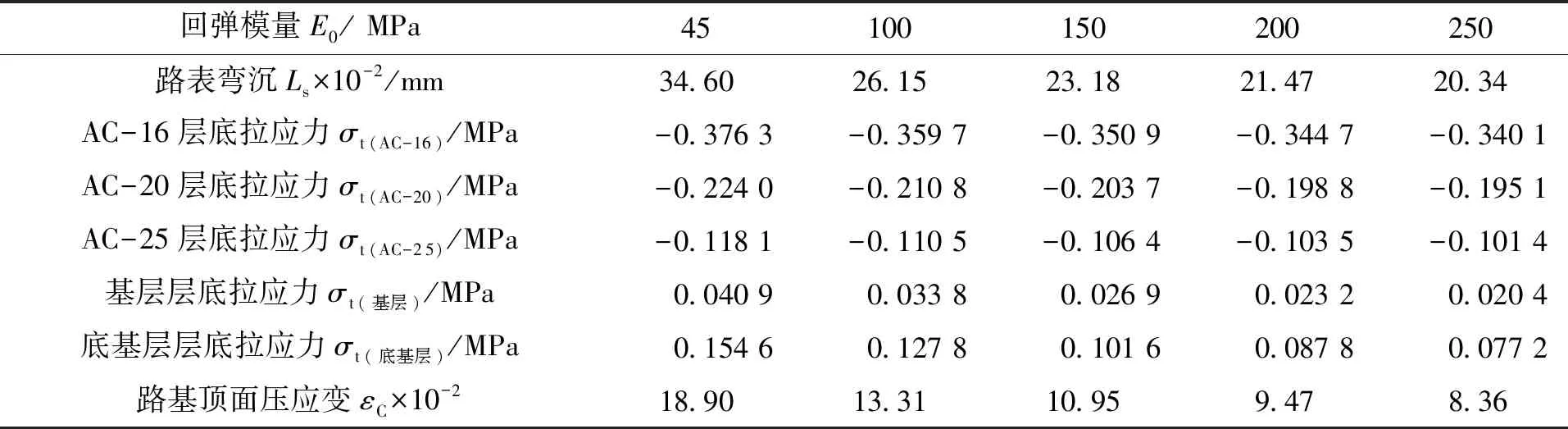
表5 路面结构计算结果Tab.5 Calculation results of pavement structure

2.2.1 宕渣路基对路表弯沉的影响

回弹模量E0—路表弯沉Ls曲线如图6所示，由图6的数据可知，选取路面结构的回弹模量E0从45 MPa升高至250 MPa，Ls减幅为24.4 %～41.2 %，由图6的整体趋势可知，随E0的增加Ls降低，当使用宕渣填筑路基时，Ls减幅趋于平缓，且相比土基所对应的Ls减少地更加明显。

2.2.2 宕渣路基对路面内部应力的影响

回弹模量E0—下面层层底拉应力σt(下面层)曲线如图7所示，回弹模量E0—基层层底拉应力σt(基层)曲线如图8所示，回弹模量E0—底基层层底拉应力σt(底基层)曲线，如图9所示。由图7～图9可知，σt(下面层)为负，即下面层层底承受压应力(σC(下面层))，E0增大时，路面结构的层底应力随之减小，且减幅逐渐减小。E0从45 MPa增加至250 MPa时：σC(下面层)减幅为6.4 %～14.1 %，σt(基层)减幅为17.3 %～50.1 %，σt(底基层)减幅为17.3 %～50.0 %。

图6 回弹模量E0—路表弯沉Ls曲线
Fig.6E0-Lscurves

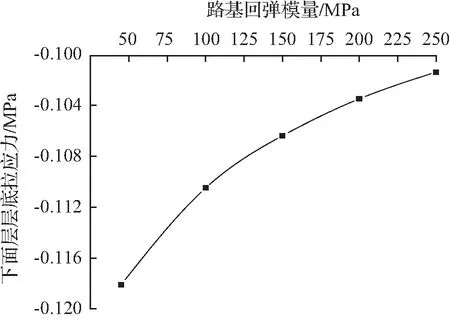
图7 回弹模量E0—下面层层底压应力σC(下面层)曲线
Fig.7E0-σC(binder course)curves

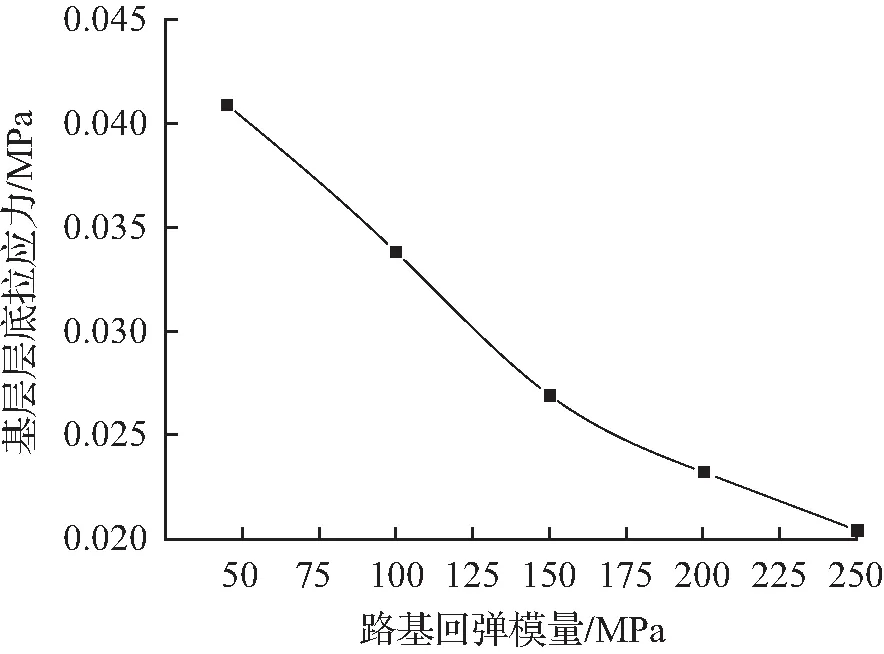
图8 回弹模量E0—基层层底拉应力σt(基层)曲线
Fig.8E0-σt(base)curves

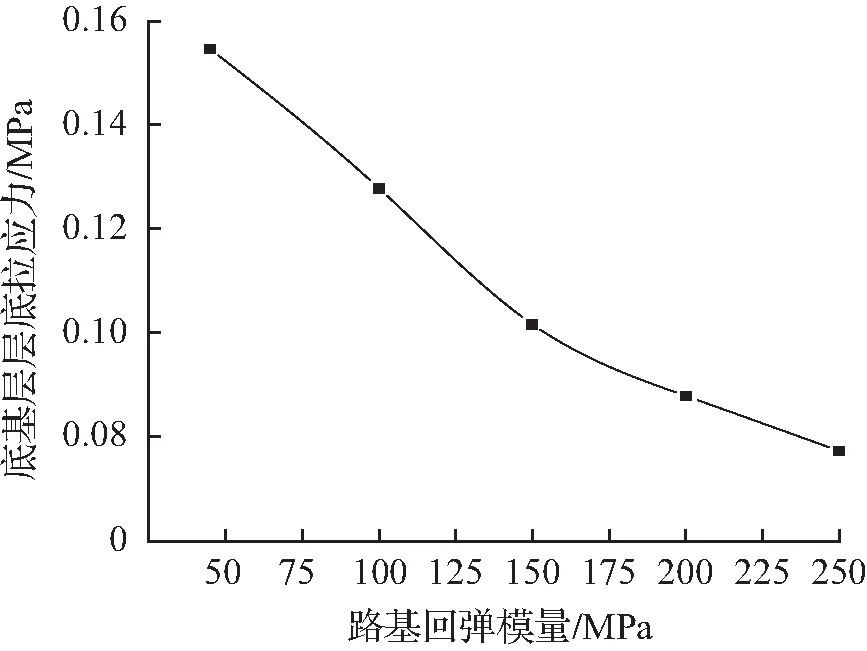
图9 回弹模量E0—底基层层底拉应力σt(底基层)曲线
Fig.9E0-σt(subbase)curves

2.2.3 宕渣路基对路基顶面压应变的影响

回弹模量E0—路基顶面压应变εC曲线如图10所示，从图10可知，选取路面结构的E0从45 MPa增加至250 MPa时，εC随之减小，且减幅逐渐减小，选取路面结构的εC减幅为29.6 %～55.8 %。由上述结果来看，E0在45～100 MPa变化时，所对应的εC改变较为敏感。

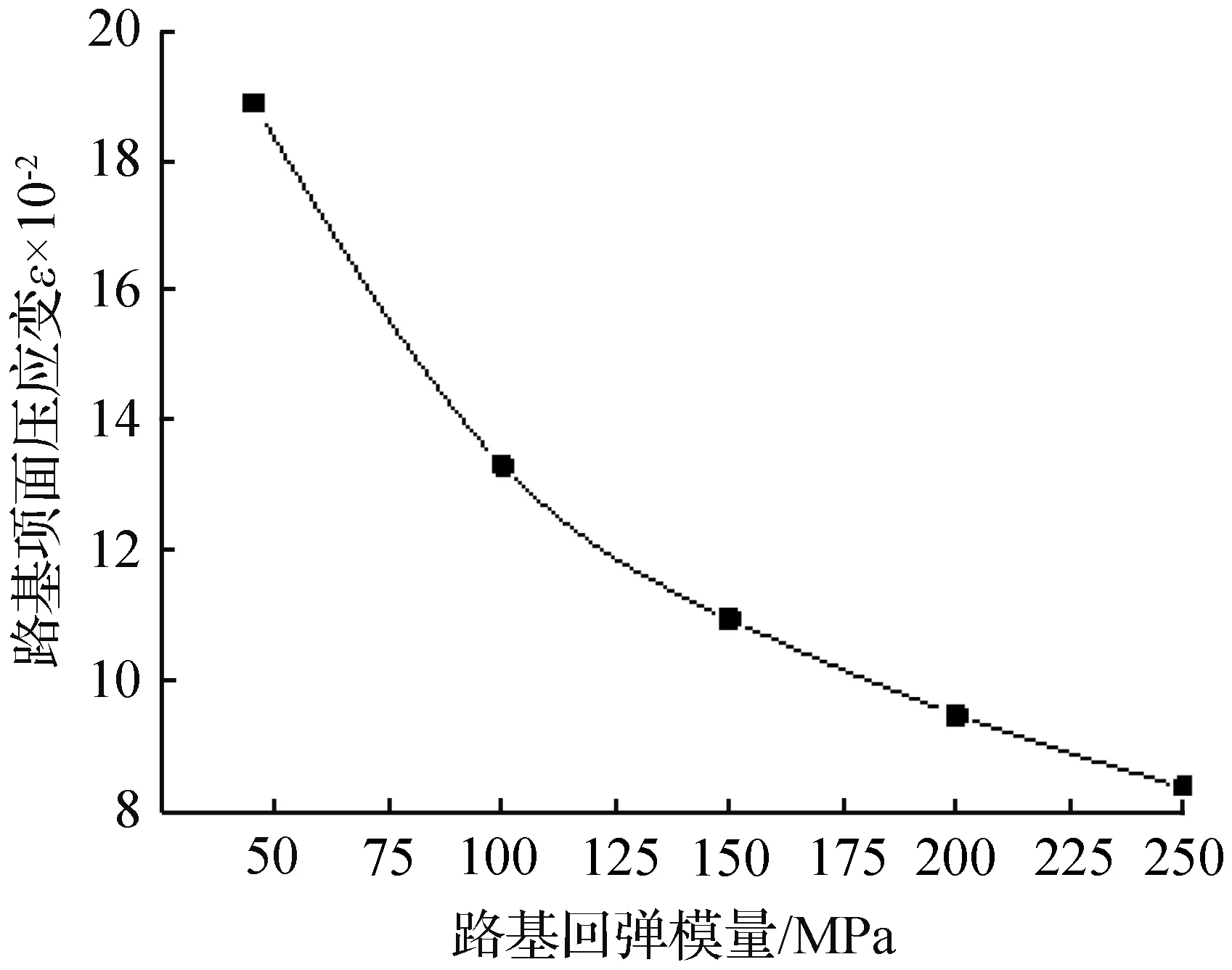
图10 回弹模量E0—路基顶面压应变εC曲线Fig.10 E0-εC curves

3 宕渣路基对水稳碎石基层厚度的影响

参考黄祁公路的材料设计参数，如表6所示[19]。将用宕渣填换土基(E0由45 MPa换为150 MPa)。设定6种不同的工况，将水泥剂量5 %的水稳碎石基层分别设定34 cm、24 cm、14 cm。层底拉应力σt和路表弯沉Ls两大指标的ABAQUS模拟结果如表7所示。

表6 路面结构材料设计参数Tab.6 Design parameters of pavement structure materials

表7 不同工况模拟计算结果Tab.7 Simulation results of different working conditions

根据上述表7中模拟的结果，将各工况的基层厚度(t)与层底拉应力σt进行数学线性回归，层底拉应力与基层厚度之间均呈对数关系，回归结果如表8所示。为了能更直观的探讨用宕渣填筑路基的效果，以及对水稳基层沥青路面结构整体的影响。将上述表7做处理，以工况1为基准。其他工况与工况1相除，两者的比值结果如表9所示。

表8 基层厚度t与层底拉应力σt的回归结果Tab.8 Regression results between the base thickness and σt

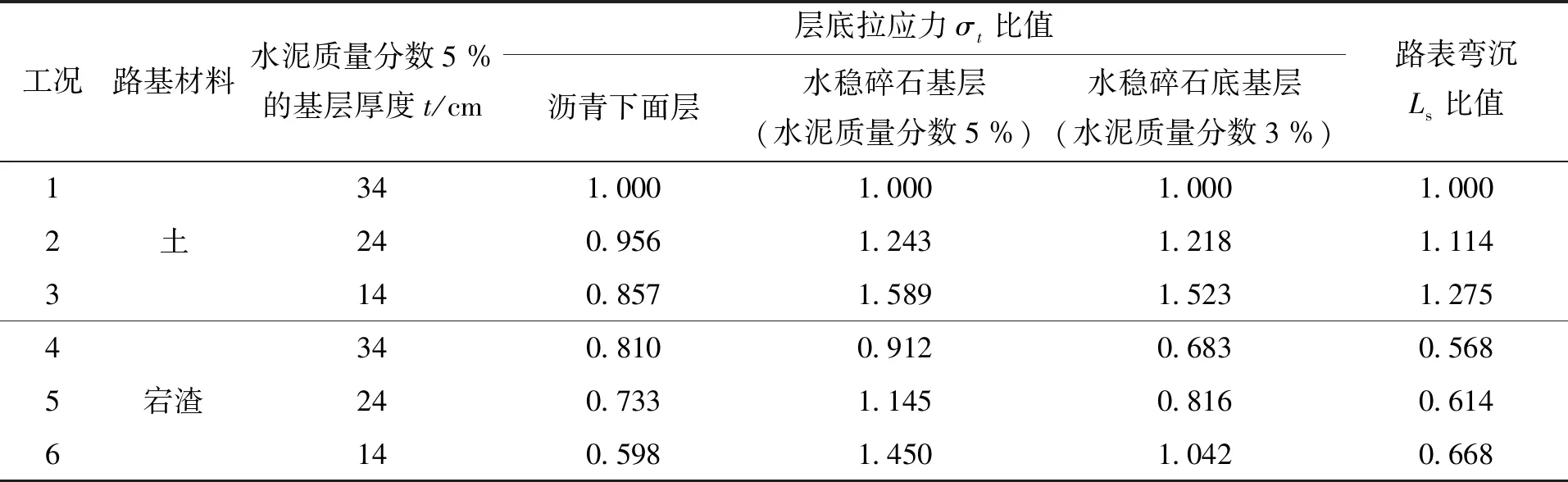
表9 不同工况模拟计算结果比较Tab.9 Comparison results of different working conditions

如表9所示，从工况4至6可以得出，路基的填筑材料为宕渣时，与传统路基材料相比较，各工况其对应的路表弯沉Ls减幅大于31 %，层底拉应力σt均有所下降。当路基的填筑材料为宕渣时，原始路面结构34 cm厚的基层减薄10 cm为24 cm时，下面层层底拉应力σt(下面层)、底基层层底拉应力σt(底基层)、路表弯沉Ls减幅分别为12.6 %、33.0 %、31.0 %。从路面结构的整体指标来看，减薄厚度的宕渣路基路面结构力学性能仍然优于普通路基沥青路面结构。通过增加路基回弹模量可以使路面结构的基层厚度适当缩减，可以减少工程投资的费用。

4 宕渣路基对超载作用下路面结构的影响

以如表6所示的路面结构为研究对象，进行宕渣路基对超载作用下路面结构的影响。超载轴换算表如表10所示[18]。ABAQUS的路面结构参数计算结果如表11所示，根据表11绘制超载对路面结构重要参数的影响曲线，如图11～图13所示，由表11和图11～图13可知，超载对于路面结构有严重危害，超载作用下路表弯沉Ls、层底拉应力σt、路基顶面压应变εC明显增加，行车荷载分别超出标准轴载60 %和120 %时，三个指标的增幅分别为35 %和67 %左右。路表弯沉Ls、面层层底拉应力σt(面层)、底基层层底拉应力σt(底基层)、路基顶面压应变εC随着回弹模量E0的增大而逐渐减小，且减幅随着E0的增加而增大。宕渣填筑路基后Ls、σt(面层)、σt(底基层)、εC减小，减幅范围分别为23.31 %～38.80 %、4.99 %～11.14 %、20.70 %～47.69 %、32.40 %～59.16 %。故通过增加路基回弹模量可以改善路面结构力学性能。

表10 超载轴换算表Tab.10 Overloadaxle load conversion

表11 超载作用下的路面结构参数结果Tab.11 Results of pavement structure parameters under overloading

图11 路表弯沉Ls—轴重曲线
Fig.11Ls-axle load curves

图12 下面层层底拉应力σt(下面层)—轴重曲线
Fig.12σt(binder course)-axle load curves

图13 路基顶面压应变εC—轴重曲线Fig.13 εC-axle load curves

5 结论

①含水率w对级配2的回弹模量E0影响最小，故建议采用级配2的宕渣土石混合料作为路基填筑材料，工程建议值为试验结果平均值244 MPa，二次函数能较好地刻画w与E0之间的关系。

②宕渣填筑路基可以显著提高回弹模量E0，改善路面结构的力学性能，路表弯沉Ls、层底拉应力σt、路基顶面压应变εC随着E0的上升而逐渐下降。

③对数函数可以很好地刻画层底拉应力σt与基层厚度之间的关系。通过增加路基回弹模量可以适当缩减水稳基层厚度，减薄厚度的宕渣路基路面结构力学性能仍然优于普通路基沥青路面结构，具有较好的经济效益。

④超载幅度分别为60 %和120 %时，路表弯沉Ls、路基顶面压应变εC、底基层层底拉应力σt(底基层)、面层层底拉应力σt(面层)的增幅分别为35 %和67 %左右，通过增加路基回弹模量可以改善超载作用下路面结构的力学性能，宕渣填筑路基后Ls、σt(上面层)、εC的减幅范围分别为23.31 %～38.80 %、4.99 %～11.14 %、32.40 %～59.16 %。