力—化耦合作用下泥页岩井眼动态破坏分析
2019-09-23朱宽亮吴晓红1贾善坡吕方3肖志强
朱宽亮*1,吴晓红1,贾善坡,吕方3,肖志强
(1.中国石油天然气股份有限公司冀东油田公司, 河北唐山063004;2.长江大学岩土力学与工程研究中心, 湖北荆州434023;3. 湖北省油田化学产业技术研究院, 湖北荆州434000)
0 引言
泥页岩井壁失稳问题是一个长期困扰石油工程界的重大技术难题,由于井眼的钻开打破了原有的各种平衡状态,受到应力卸载、液压梯度和化学梯度的共同作用,再加上泥页岩本身自有的硬脆性和水敏性,给钻井工程带来诸多意想不到的复杂问题[1-2]。硬脆性泥页岩粘土矿物含量高、微裂缝发育,在实钻过程中,泥页岩裂缝自吸水及长时间浸泡引发的掉块经常造成钻具阻卡、电测遇阻等井下复杂情况,严重影响钻井效率。因此,研究中深层泥页岩水化特性和坍塌机理,对于提高钻速、减少井下复杂情况发生具有重要意义。
国内外的学者已经对有关泥页岩井壁稳定问题进行了大量的研究工作,其研究成果根据问题的不同以及复杂性表现出不一致性,并且每一种理论都有一定的局限性,使得问题的讨论不够完善。崔莹等[3]依据井壁力学模型和双剪统一强度理论推导了垂直井井壁坍塌压力统一解表达式,但对于钻井液渗透、地层开挖及浸泡作用考虑的不够全面;YEW 等[4]提出了热弹性比拟法,即将自由水扩散比拟成热扩散,水化膨胀应力比拟为变温膨胀应力,建立了坍塌分析模型,但是该模型未考虑钻井液与泥页岩之间的相互作用;MODY等[5]利用半透膜渗透压思想,分析了化学势差作用下的等效孔隙压力,建立泥岩井壁坍塌模型,但是该方法否定了离子运移对泥岩水化的影响,忽略了因浸泡造成的地层强度弱化;LOMBAR等[6-7]考虑泥页岩—钻井液电化势和离子运移、泥页岩—钻井液体系中流体流动和溶质扩散过程的非线性、流体流动和离子运移对固体变形的影响,建立泥页岩井壁稳定流—固—化耦合模型,但是模型中存在过多难以确定的参数,不便实际应用,且未考虑地层开挖卸载和塑性变形。泥页岩地层一旦被钻开,平衡状态遭到了破坏,井壁围岩强度、井壁应力和孔隙压力均随钻井液的接触时间而变化[8]。因此,一个有效的井眼预测模型应能够体现出发生在泥页岩地层中的力学和物理化学动态过程。
中深层岩性圈闭是东部油田近年勘探开发的重点,埋藏深度超过4000m,发育大段硬脆性泥页岩,因其水化效应显著、裸眼浸泡时间长,同时存在裂缝,井眼失稳问题突出[9]。笔者在前人研究的基础上,通过对硬脆性泥页岩理化性能、微观结构和岩石力学特性分析,考虑钻井时岩石的实际卸载过程、强度弱化和塑性变形特性,建立了泥页岩井眼动态破坏耦合模型,探讨井眼动态失稳机理。
1 硬脆性泥页岩井眼坍塌机制
1.1 地层矿物组成
利用X-射线衍射仪,对研究工区内3口井沙河街组泥页岩段岩芯进行全岩矿物和粘土矿物测试。泥页岩矿物以粘土、石英为主,此外不同程度发育有长石、方解石、白云石等,脆性矿物(石英、长石、方解石)较为发育,其中石英含量为6.71 %~39.94 %,粘土含量整体较高,含量为19.09 %~43.06 %,粘土矿物均以伊利石、伊/蒙混层为主,在沙河街组均未见蒙脱石发育,其中伊利石相对含量为34.47 %~56.64 %,伊/蒙混层含量6.72 %~39.74 %。采用岩石矿物组成方法评价研究工区沙河街组泥页岩脆性[10],三口井对应泥页岩脆性分别为0.664、0.809和0.569,平均值为0.681,高于北美泥页岩脆性指标下限值0.4,该工区泥页岩属于脆性岩石。
1.2 泥页岩细观构造
利用扫描电镜分析泥页岩微观构造形态,扫描结果如图1所示。沙河街组泥页岩虽然压实程度较高、结构紧密、胶结程度好,但是其存在较为发育的微裂隙以及较为发育的微孔洞等,为钻井液在钻井过程中进入地层提供了通道。由于受到压差和毛细管力的作用,钻井液沿着微裂隙或微孔洞侵入地层,提高了钻井液和地层中的粘土矿物、有机质的作用几率以及作用程度,致使地层岩石力学强度降低,加剧井眼破坏。

(a) 微裂缝

(b) 微孔洞
图1 泥页岩扫描电镜图像
Fig.1 SEM images of mudstone core
图2为水化作用下泥页岩微裂缝形态变化特征,水化作用导致泥页岩内部微裂纹的萌生、扩展或分叉,且流体沿微裂纹渗入岩石内部,加剧泥页岩破坏。

(a) 侵入前

(b) 侵入后48 h
图2 水化作用下泥页岩裂隙变化特征
Fig.2 Change of micro-crack in mudstone due to hydration effect
1.3 钻井液体作用对泥页岩力学性质的影响
由于泥页岩钻井岩芯获取困难,且用于开展三轴试验的有效岩样非常有限,而压入硬度试验对岩样形状要求较低,可进行大量的测试分析。采用史氏压入硬度法测试钻井液对泥页岩压入硬度的影响规律,用以描述泥页岩强度的变化特征。
选取同一位置泥页岩分别开展原岩、浸泡钻井液6 h、12 h的压入硬度试验,共开展3组,试验结果如图3所示。可以看出,泥页岩岩样的压入硬度随着浸泡时间的增加而逐渐下降,浸泡时间越长,压入硬度的下降幅度越大,泥页岩在钻井液浸泡下的压入硬度减小的特征表明了地层强度随钻井液浸泡时间的增加而降低[11]。

图3 压入硬度随着钻井液浸泡时间的变化Fig.3 Change of indentation hardness with the drilling fluid soaking time
2 泥页岩井眼动态破坏耦合模型
2.1 吸水扩散模型
从钻开井眼开始,泥页岩便与钻井液接触,由于受到水力梯度和化学势梯度的驱动,致使水和离子发生传递。泥页岩的吸水过程十分复杂,令w表示随空间和时间变化的吸附水量的质量分数,根据质量守恒方程可建立水分的扩散方程[12]:
(1)
式中:Cf为泥页岩的吸水扩散系数,cm2/h。吸水扩散系数是一个表征地层水变化传递速度的参数,可以通过泥页岩吸水扩散试验测得。相应的边界及初始条件按远场和井壁的含水量来确定。
2.2 压力传递模型
认为泥页岩具有半透膜特性,钻井液进入地层后,在化学势差作用下流体中的部分离子发生运移,使地层水活度发生了改变。活度是指盐溶液和纯水的逸度比,是表征溶液中化学势强弱的一个参数。钻井时地层流体的活度计算模型为:
(2)
式中:D为活度扩散系数,m2/h。活度扩散系数是表征地层水活度传递快慢的一个参数,可根据页岩压力传递试验数据拟合得到。
钻井液进入地层后,地层的孔隙压力将会由于地层流体与钻井液之间的化学势差和水力压差而导致重新分布。综合考虑化学势差和流体孔隙压力,建立孔隙压力计算模型[13-14]:
(3)
式中:p为地层流体压力,MPa;k为地层渗透率,达西;υ为流体黏度,MPa·s;C为流体压缩系数,Pa-1;φ为孔隙度,无因次;Im为膜效率,无因次;R为气体常量,8.314 m3·Pa/(K·mol);T为绝对温度,K;V为水的偏摩尔体积,1.80×10-5m3/mol;θ为钻井时地层流体活度,无因次;θshale为泥页岩中地层水活度,无量纲。
2.3 井眼破坏模型
根据Biot有效应力原理,有效应力可表示为:
(4)
式中:σij为总应力张量;p为孔隙流体压力,规定以压力为正;α为Biot系数;δij为Kronecker符号。
基于压力传递模型、有效应力原理和弹塑性力学理论,得到综合考虑化学势变化和流体流动与骨架变形耦合的本构方程,即:
(5)

井眼破坏准则采用修正的Drucker-Prager准则,屈服函数定义为:
(6)

泥页岩强度参数随地层含水量变化,结合相关试验成果[14],强度参数近似随着含水量动态线性衰减,将式(1)和式(6)进行耦合,即可建立水化泥页岩强度弱化动态模型,即:
(7)
式中:c0为初始含水量为w0时的粘聚力;φ0为初始含水量时的内摩擦角;Ks为粘聚力系数;Ls为内摩擦角系数。
2.4 模型的数值实现
基于以上分析,笔者采用解耦的数值处理方法,水分扩散方程是相对独立的,可首先进行求解,然后将压力传递模型和固体变形进行间接协同耦合求解,共涉及到ABAQUS软件内嵌的2个计算模块,即岩土固结模块和质量扩散模块。
尽管岩石流—固耦合场和质量扩散场存在较大的差别,但本质上包含了两个基本的内容即线性化和时步离散(或载荷增量),可将流—固体场和扩散场的计算按两个独立的系统分别进行设计,通过数据通讯方式,使每一时步上的参数耦合得以实现,在每一时步上不断地修正相关的系数,而这种相互修正又是在一系列时步上交叉进行的。笔者在前期THM耦合方法研究的基础上[15],以MATLAB为平台、ABAQUS为求解器,开发泥页岩井眼动态破坏计算软件,通过编制ABQMAIN子程序实现各计算模块之间数据的存储和通讯,强度参数弱化通过USDFLD子程序来实现。
3工程实例分析
3.1 计算模型及参数
以研究工区内的W井为研究对象,井深4 700 m,钻遇地层主要为明化镇组、馆陶组、东营组和沙河街组地层。图4为几何模型示意图,用于模拟4 200~4 300 m井段沙河街组硬脆性泥页岩井眼稳定性。模型的长度为15 m,长宽比为1∶1,井眼半径为0.11 m。根据井眼的对称性,有限元模型考虑井眼的四分之一,采用平面应变四边形单元对模型进行离散,网格划分如图5所示。
模型边界条件定义如下:BC和CD分别施加最大和最小水平地应力,AB边为水平滑移边界,DE边为垂向滑移边界,模型内部分布有初始孔隙压力、初始应力、初始地层含水量、初始地层水活度,开挖之后,AE边施加井眼液柱压力、含水量条件、钻井液活度。
用于模拟井眼渐进破坏过程的计算步骤为:第一阶段为地应力平衡计算;第二阶段是开挖阶段,通过单元生死模拟钻进开挖过程[16],然后施加液柱压力;第三阶段是水化扩散阶段,井孔内、外发生渗流扩散效应,井眼围岩强度因水化减弱,本阶段模拟开挖完成后25 d内井壁的破坏过程。

图4 物理模型示意图Fig.4 Schematic diagram of physical model

图5 网格划分
Fig.5 Meshes of analysis model
取自W井沙河街组泥页岩进行原岩三轴压缩力学特性测试,测试结果如表1所示。采用Mohr-Coulomb强度准则进行拟合,可得原岩粘聚力值为24.14 MPa,内摩擦角为21.7°。另外,对5个泥页岩岩样进行了巴西劈裂试验,泥页岩的抗张强度为1.13~6.09 MPa,平均值为4.41 MPa。
根据室内试验、现场资料、测井资料以及邻井地质资料获得计算所需基本参数:上覆岩层压力91.63 MPa,水平最大地应力81.22 MPa,水平最小地应力68.72 MPa,地层压力51.45 MPa,地层渗透率1.01×10-4mD,孔隙度9 %,钻井液活度0.85,地层水活度0.80,活度扩散系数5×10-9m2/s,膜效率0.2,吸水扩散系数量级为9.5×10-9m2/s,地层初始含水量2 %,饱和含水量10 %,粘聚力系数Ks为2.71MPa,内摩擦角系数Ls为2.50°。

表1 原岩三轴压缩试验结果Tab.1 Results of triaxial compression test
3.2 计算结果
由于地层钻开致使岩石应力卸载对应的时间相对较短,开挖阶段钻井液对地层强度的影响可以忽略,开挖后井眼破坏区分布如图6所示。井眼在平行最小地应力方向发生剪切破坏,在这一方向尺寸变大,破坏区为近似的椭圆形状,与井下成像观测和室内试验结果一致。钻井液当量密度为1.05、1.1、1.2和1.3时对应的最大塑性应变值分别为0.55 %、0.46 %、0.29 %和0.16 %。钻井液密度越大,塑性区越小,适当提高钻井液密度,有利于井壁保持稳定。
图7为地层钻开后井眼围岩含水量分布图。含水量随着距井壁距离的增大而逐渐减小并趋于最小值2 %,地层钻开后早期,含水量变化较为剧烈,存在一定的波动,此后含水量变化速率随浸泡时间的增大而减小。
图8为地层岩石粘聚力分布图。地层强度分布规律与含水量分布相似,这是因为地层岩石的粘聚力和内摩擦角均受含水量控制,随着含水量的变化而变化。

(a) 钻井液密度1.05

(b) 钻井液密度1.3
图6 开挖后井眼塑性区分布
Fig.6 Plastic strain distribution of wellbore after excavation

图7 地层钻开后井眼含水量分布
Fig.7 Water content distribution ofwellbore after drilling

图8 地层钻开后粘聚力分布
Fig.8 Cohesion distribution ofwellbore after drilling
钻井液密度为1.05和1.3时井眼渐进破坏过程如图9和10所示。垂向(y方向)的破坏程度和范围明显大于水平向(x方向),破坏区呈椭圆形状,当钻井液密度为1.05时,浸泡1 d、5 d、10 d和15 d后的最大塑性应变值分别为1.37 %、2.13 %、2.73 %和3.18 %,而当钻井液密度为1.3,浸泡1 d、5 d、10 d和15 d后的最大塑性应变值分别为0.79 %、1.09 %、1.31 %和1.46 %,较小的钻井液密度加剧了井眼渐进破坏。就井眼破坏深度而言,在井眼浸泡早期,井眼破坏区域增加较为迅速,此后趋于稳定并逐渐呈线性增加趋势。
3.3 与现场结果对比
W井采用密度为1.2 g/cm3的抗高温防塌钻井液体系(聚硅氟)钻进沙河街组地层,钻进过程中井壁基本稳定,仅有几次轻微井塌,平均机械钻速1.78 m/h。将钻井液当量密度为1.2时的数值模拟结果与现场实测资料进行对比分析,通过获取不同时刻下测线AB和ED对应的塑性区范围,并取其平均值作为井径扩大值,将井径扩大值与钻头外径的比值定义为井眼扩大率,井眼扩大率预测结果如图11所示。井眼扩大率随钻井液浸泡时间的增大而增大,在早期阶段井眼扩大速率较快,随着时间的增长,井眼扩大速率减缓并趋于稳定。

(a) 1 d

(b) 5 d
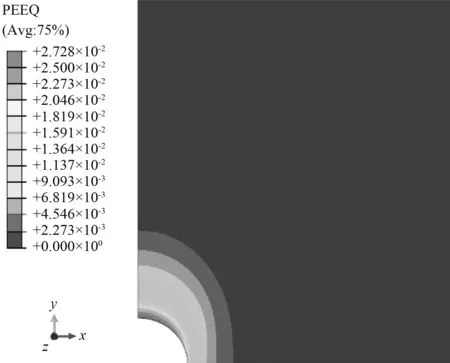
(c) 10 d

(d)15 d
图9 钻井液密度为1.05时井眼动态破坏过程
Fig.9 Progressive failure process of wellbore with a drilling fluid density of 1.05

(a) 1 d

(b) 5 d

(c) 10 d

(d) 15 d
图10 钻井液密度为1.30时井眼动态破坏过程
Fig.10 Progressive failure process of wellbore with a drilling fluid density of 1.30
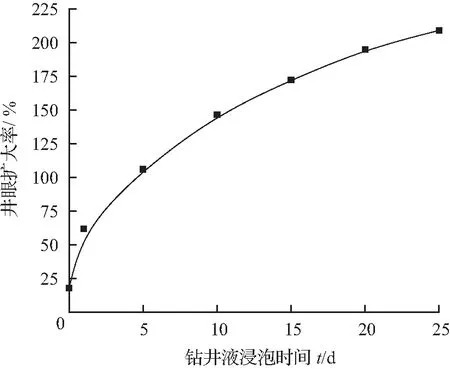
图11 井眼扩大率随时间变化曲线Fig.11 Curve of wellbore enlargement with time
根据图11所示的计算结果,当井眼钻开后,井眼扩大率计算值为18.1 %,与现场出现的轻微井塌现象一致。中途起钻和测井工程中曾返出大量掉块,接立柱困难,短起下钻必须使用倒划眼才能进行,裸眼段存在多处大井眼井段,其中4 200~4 280 m段井眼扩大率在74 %~112 %之间(见表2),井眼扩大率计算结果为106 %。随后进行中途测试,至中途测试下钻通井泥浆浸泡地层长达19 d,掉块多,造成地层失稳,井壁大段坍塌,而本文预测的井眼扩大率已超过170 %,垮塌严重,与实际钻井基本吻合,说明本文预测模型可以有效反映泥页岩井眼动态破坏过程。

表2 井径扩大率实测记录Tab.2 Measurement of diameter expansion
4 结论
①综合有效应力原理、吸水扩散和压力传递模型,建立可考虑化学势变化和流体流动与骨架变形耦合的泥页岩井眼渐进破坏分析模型,以ABAQUS软件为求解器,编制了计算程序,利用该模型可有效模拟硬脆性泥页岩井眼动态破坏过程,计算结果与实际钻井基本吻合,验证了提出模型的有效性。
②井眼扩大率随钻井液浸泡时间的增大而增大,在同一浸泡时间下井眼扩大率随着钻井液密度的增大而减小,水化效应对井眼渐进破坏的影响要远大于渗流场的影响,水化对井眼的渐进破坏起着非常重要的作用。
③沙河街组硬脆性泥页岩中,伊/蒙混层矿物和伊利石含量较高、微裂隙发育,水化致使岩石强度降低、微裂隙逐渐变大、掉块,这是硬脆性泥页岩地层钻井井壁失稳的根本原因,有效的解决方法是减少裸眼井眼浸泡时间,强化封堵和提高钻井液的抑制能力。
