弹性基底非加载边弹性转动约束矩形板线性受压屈曲分析
2019-09-23向勇斌1莫时旭1郑艳2
向勇斌1,莫时旭1,郑艳2
(1.桂林理工大学土木与建筑工程学院, 广西桂林541004;2.广西建筑新能源与节能重点实验室, 广西桂林541004)
0 引言
我国钢材的产量历年攀升,国家出台相关支持政策推动钢结构在建筑行业中的应用,而钢—混凝土组合结构作为一种新型的结构,得到了快速的发展,同时钢结构的稳定性问题在结构设计中越来越受到重视,国内外学者近年来对矩形薄壁钢板屈曲问题的理论分析主要分为两类。
一类是双向屈曲问题,国外学者TIMOSHENKO等[1]利用能量法提出了在不同边界条件下、不同面内作用力下矩形薄板自由屈曲的理论计算模型;国内学者童根树等[2]采用有限单元法研究了四边简支矩形板在局部承压、弯曲与剪切联合作用下的弹性屈曲行为;刘沐宇等[3-5]采用Rayleigh-Ritz法研究了弹性转动边界约束钢—混组合梁腹板的剪切屈曲。
另一类是单边屈曲问题,国外学WRIGHT等[6-8]研究了混凝土填充钢管的局部屈曲问题;UY等[9]研究了组合截面墙的局部屈曲问题;OEHLERS等[10-11]研究了组合截面梁在压力和弯曲作用下的屈曲问题;WRIGHT等[12]使用Timoshenko能量法研究了长薄板的单边屈曲问题;SMITH等[13]采用Rayleigh-Ritz法研究了弹性支承薄板的屈曲行为;国内学者何保康等[14]研究了矩形钢管混凝土柱管壁局部屈曲性能;莫时旭等[15-19]采用Rayleigh-Ritz法研究了薄板基于刚性基底的非加载边弹性转动约束面内均匀受压和线性压力作用下的局部屈曲问题;毛佳等[20]采用Rayleigh-Ritz法研究了基于弹性基底的非加载边弹性转动约束面内均匀受压作用下薄板的局部屈曲问题。
目前国内关于弹性基底的非加载边转动约束面内非均匀受压下的薄板单向屈曲问题的研究尚不充分,文章采用Rayleigh-Ritz法推导了上述边界条件下矩形薄板的单向屈曲计算公式,进一步分析了弹性基底刚度K、边界转动约束刚度ξ、长宽比γ、压力梯度λ、厚度t对临界屈曲系数κ的影响,理论计算公式所得κ值与文献[1,15-20]中的κ值一致,且各参数影响曲线相似。
1 理论计算
Rayleigh-Ritz法,是应用势能驻值原理求解稳定问题题的一种近似方法。使用静力平衡的方法求解稳定问题,需要用微分方程来求解,然而有许多微分方程的通解较难求得,这就需寻找一些近似的容易求解的方法。Rayleigh-Ritz法的特点,是采用具有几个广义坐标的位移函数近似地代替真实的位移曲线,也就是将原来为无限个变量的泛函变分问题转化为有限个变量的函数极值问题来处理。这样,根据势能驻值原理的极值条件,用导数求极值问题的方法,将求解微分方程的转化为求解代数方程。
计算模型见图1,其相关参数如下:
a为矩形薄板长度;
b为矩形薄板宽度;
E为钢材弹性模量;
t为薄板厚度;
ν为钢材泊松比;
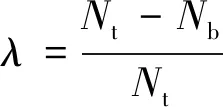
ξ为边界弹性转动约束刚度;

K为弹性支承刚度;
Nt为端部压力;
Nb为端部拉力;


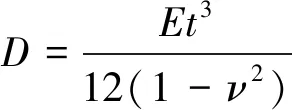

根据已有文献研究结论,矩形薄板屈曲后的模态为横向一个半波、纵向连续多个半波,本文考虑纵向屈曲成m个半波,故选择位移函数为:
(1)
式中:φ0~φ4由边界条件确定。
W(x,0)=W(x,b)=W(0,y)=W(a,y)=0,
(2)
(3)
(4)
将式(1)代入式(2)、(3)、(4)得:
φ0=0;φ1=φ1;φ2=Xφ1;φ3=-2(1+X)φ1;φ4=(1+X)φ1,
β=φ1α。
将结果代入式(1)得:
(5)
弹性支承势能Uk、板弯曲应变能Ue、边界转动约束势能Uξ和轴向载荷Nx所作功V分别为:
(6)
(7)
(8)
(9)
根据最小势能原理得:
δΠ=δUe+δUξ+δUk-δV=0,
(10)
(11)
将求解泛函变分问题转化为求解关于β线性方程组非零解的问题,由其系数行列式为零,得临界荷载为:
(12)
(13)
其中:η1=31+11X+X2η2=3024+3528X+504X2η3=612+216X+24X2。
2 参数分析
2.1 长宽比分析
当X=0,λ=0,Y=0,工况为四边简支不同长宽比矩形板均匀受压双向屈曲,根据方程(13)可得
(14)
方程式(14)与文献[1]中方程一致,根据方程(14)取不同的长宽比,计算得出一阶(m=1)、二阶(m=2)屈曲模态相关数据,见表1、如图2所示。

表1 不同长宽比下屈曲系数Tab.1 Relation between γ and κ

图2 γ-κ关系Fig.2 Relation between γ and κ
从表1、图2中可以得出结论:
一阶(m=1)屈曲模态长宽比γ小于1时,屈曲系数κ随着长宽比γ的增大而降低,长宽比为γ=1时,κ为最低值,此κ后随着长宽比γ的增大而增加;二阶(m=2)屈曲模态长宽比γ小于2时,屈曲系数κ随着长宽比γ的增大而降低,长宽比为γ=2时,κ为最低值,此κ后随着长宽比γ的增大而增加,与文献[1]得出的结论一致。
根据方程(14),可求得一阶曲线与二阶曲线在点γ=1.414处相交。对于长宽比小于1.414的薄板,屈曲模态为一阶;长宽比大于1.414的薄板,屈曲模态为二阶。即临界屈曲曲线为一阶曲线左半部分和二阶屈曲曲线右半部分组合而成,对于m≥3的高阶模态,可采用类似方法推导。
2.2 压力梯度分析
当m=1,X=0,γ=1,Y=0,工况为四边简支正方形板双向屈曲(一阶)时,根据方程(13)计算得出相关数据,见表2、如图3所示。

表2 不同压力梯度下屈曲系数Tab.2 Relation between λ and κ
从表2、图3中可以得出结论:λ为0时即均匀压力,κ=4.002;λ为1时即三角形压力,κ=8.102 8,随着λ的增加,κ值的增加,即临界屈曲系数随着压力梯度的增大而增大。
2.3 弹性转动约束系数分析
当m=1,λ=0,γ=1,Y=0,工况为加载边简支非加载边弹性约束正方形板均匀受压双向屈曲(一阶)时,根据方程(13)计算得出相关数据,见表3、如图4所示。

表3 不同转动约束系数下的屈曲系数Tab.3 Relation between X and κ

图3λ-κ关系
Fig.3 Relation betweenλandκ

图4X-κ关系
Fig.4 Relation betweenXandκ
从表3、图4中可以得出结论:X=0时即非加载边简支,0 当m=1,X=0,λ=0,γ=1,工况为四边简支不同支承刚度正方形板均匀受压双向屈曲(一阶)时,根据方程(13)得: (15) 假设E=2.1×1011Pa,K=1×105Pa,b=1 m,a=1 m,由方程(15)得到相关数据,见表4、如图5所示。 表4 不同厚度下屈曲系数Tab.4 Relation between κ and t 从表4、图5中可以得出结论: κ是t的单调递减函数,即钢板厚度t的增加,屈曲系数κ减少,出现单调递减趋势。这是因为钢板厚度较薄,钢板本身抗弯刚度较小,基底的刚度对钢板提供的约束相对较大,故表征不同边界条件的临界屈曲系数较大,当钢板厚度较厚时,钢板本身抗弯刚度较大,基底的刚度对钢板提供的约束相对较小,故临界屈曲系数较小。 从表5、图6中可以得出结论:κ是K的单调递增函数,则支撑刚度K的增加,屈曲系数κ增加,与文献[20]所得结论一致。 当m=1,X=0,λ=0,γ=1,工况为四边简支不同支承刚度正方形板均匀受压双向屈曲(一阶)时,根据方程(15),假设E=2.1×1011Pa,t=0.01 m,b=1 m,a=1 m,由方程(15)得到相关数据,见表5、如图6所示。 表5 不同支承刚度下屈曲系数Tab.5 Relation between K and κ 图5κ-t关系 图6K-κ关系 ①采用Rayleigh-Ritz法得到了弹性基底上非加载边弹性转动约束矩形板面内非均匀受压条件下弹性屈曲计算公式,方法中假设的位移函数符合位移和力学边界条件,形式简单、计算方便,该方法计算结果与文献[1,15-20]中的计算值相比很吻合,该计算理论有广泛的适用性。 ②矩形薄板临界屈曲系数随着压力梯度的增大而增大;矩形薄板非加载边弹性转动约束系数X=0时即可视为非加载边简支,0 ③在实际工程应用中,转动约束系数X、基底刚度K、压力梯度λ、长宽比γ等参数可以计算得出,在X、K、λ、γ确定的前提下,为了避免矩形薄板发生局部屈曲,致使构件承载力降低,可通过限制矩形薄板的宽厚比,确保矩形薄板不出现屈曲现象。 ④文章考虑基于弹性基底的面内非均匀受压下矩形薄板的屈曲行为,实际工程中的薄板受力较为复杂,面内存在剪切力和非均匀压力的同时作用,这种复杂受力条件下的理论屈曲公式较难推导。2.4 厚度分析

2.5 基底刚度分析

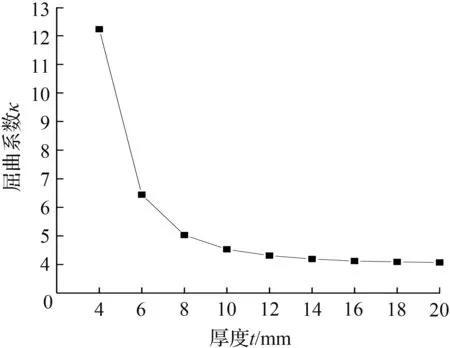
Fig.5 Relation betweenκandt
Fig.6 Relation betweenKandκ3 结语
