Rossler混沌系统单一状态变量耦合同步研究

蒋 楠

(山西广播电视大学 公共基础学院,山西 太原 030027)

0 引言

由于混沌系统具有对初始条件敏感性、长期不可预测性和伪随机性等特点,被广泛应用于保密通信、扩频通信[1-2]、信息图像加密[3-4]等研究领域。其中混沌原理在保密通信的应用中,需要发射终端的混沌系统与接收终端的混沌系统达到同步,因此混沌系统同步控制方法是保密通信的核心内容,近几年受到了广泛关注,并成为研究的热点。混沌同步是指驱动系统的轨道收敛于响应系统轨道的同一个值,学者们提出了许多混沌系统同步控制的方法,比如投影控制同步法[5-6]、自适应控制同步法[7]、主动控制同步法[8]、耦合同步控制法[9]和非线性控制同步法等。

Rossler系统仅含有一个非线性项且存在复杂混沌行为,许多学者对该系统进行了深入的研究,得到了大量的研究结果。文献[10]研究了Rossler系统在参数不确定的情况下实现了自适应同步;文献[11]利用参数识别方法,实现了超混沌Rossler 系统的自适应同步;文献[12]设计了主动控制器,实现了Rossler系统与统一混沌系统的渐近同步。在实际工程中,耦合同步[13]的收敛速度较快、应用较为广泛,主要适用于子系统不能分解的混沌系统,其关键在于耦合强度的确定。耦合同步主要包括单向同步和双向同步。由于双向同步的驱动响应系统互相影响,驱动系统受到干扰,此方法较为少用。单向耦合同步中驱动系统不受干扰,仅对响应系统中的系统状态变量进行耦合,是一种有效且易于实现的方法。文献[14]通过函数耦合实现了Duffing系统的混沌同步。文献[15]通过单向耦合,利用Lyapunov稳定性定理,采用全局同步法分别证明了Lorenz系统与Chen系统实现自同步的可靠性。文献[16]基于Lyapunov稳定性理论,构造了Lyapunov函数,实现了Chen超混沌系统的线性耦合同步。文献[17]针对非线性Chua电路,实现了系统的线性耦合同步。

上述文献所研究的混沌同步问题中,驱动系统都需要设计若干个状态变量来控制响应系统,但在通信工程的实际操作中仅发射单个状态变量。基于此，本文减少系统状态变量的耦合数目,仅对单个系统状态变量进行耦合,从实际需要出发改进了单向耦合同步法,利用Routh-Hurwitz稳定性准则,判定误差系统系数矩阵的特征值符号,通过推导同步误差渐近稳定耦合系数所需要满足的充分条件,使Rossler混沌系统达到同步,更具有现实研究价值意义。

1 Rossler系统单一状态变量耦合同步

1.1 系统模型

Rossler系统自1976年被发现以来,已经得到深入的研究。其主要优点在于结构简单,却具有非常复杂的混沌特性,它的方程组为:

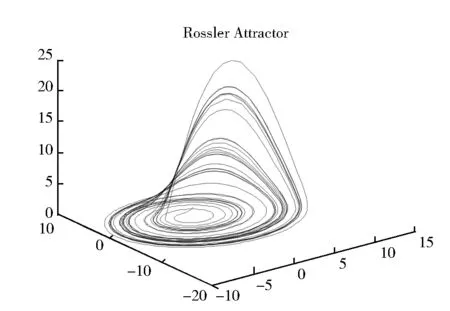
图1 Rossler吸引子Fig.1 Rossler attractor

式中:a,b,c为参数；x1,y1,z1为控制变量。当a=0.2,b=0.2,c=5.7时,系统呈混沌状态,此时Rossler系统的吸引子相空间图如图1所示。本文以Rossler系统为例提出混沌系统的单一状态变量耦合同步方法。

为了实现Rossler 系统的单一状态变量耦合同步,选取Rossler 系统分别作为驱动系统(1)和响应系统(2):

(1)

(2)

式中:k1,k2,k3为耦合系数。在混沌系统耦合同步问题中,只有适当的耦合强度才能实现同步,其中Lyapunov指数法和Lyapunov函数法是确定耦合强度的主要方法。由于线性系统理论不适用于非线性系统,Lyapunov函数的选择没有普遍适用法,仅凭经验确定,不具有科学性和准确性;误差系统的Lyapunov指数的计算量较大,甚至无法计算,因此耦合强度的确定较为困难。由于在实际应用中,通常只发射单一变量,因此改进单向耦合同步法,选取响应系统(3),对一个系统状态变量耦合,从而实现混沌系统同步。

(3)

式中:k为耦合系数。定义同步误差为:

(4)

则为了实现系统(1)与系统(3)的同步,由(3)减(1)得到误差系统:

(5)

误差系统的系数矩阵为:

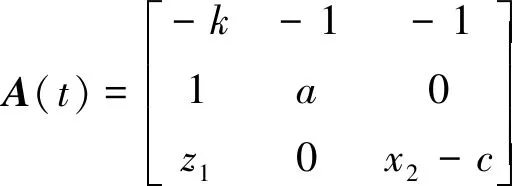
(6)

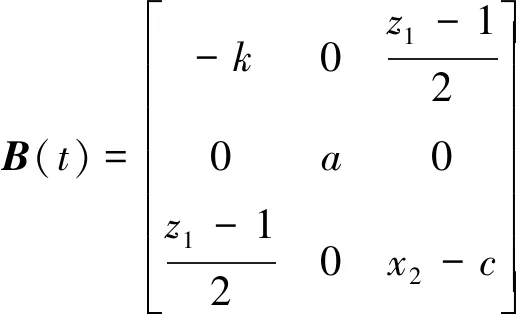
(7)

根据对称矩阵B(t)的特征值等于系数矩阵A(t)的特征值实部,设λa为B(t)的最小特征值、λb为B(t)的最大特征值。由文献[18]得到如下引理。

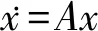
(8)

若∀ε>0,∃λb<-ε,则对于任意给定的初值x(0),x(t)收敛为零。

如果式(7)解满足式(8),则误差系统e(t)收敛为零,即Rossler混沌系统达到渐近同步。

1.2 Rossler系统单向耦合同步及稳定性分析

定理如果耦合系数k满足如下条件:

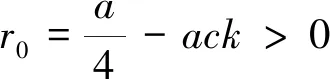
(9)

s0=ak+ac(a-c)+ck(c+k)+(a-k)(k-a+2c+ak)-3ack>0

(10)

p=c+k-a>0

(11)

则对于任意初始值,当t→∞,单一耦合的Rossler系统达到渐近同步。

证明对称矩阵B(t)的特征多项式为:

λ3+pλ2+qλ+r=0

(12)

式中:p=c+k-a-x2,

令s=pq-r,则:

ck(c+k)+(a-k)(k-a+2c+ak-3ack)=s0

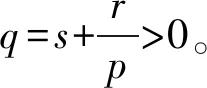
根据Routh-Hurwiz稳定性准则,若满足p>0,q>0,r>0,s>0,则特征多项式(12)的所有特征值均小于零。此时,误差系统(5)的解满足引理,误差系统e(t)收敛为零,即Rossler混沌系统实现单一状态变量耦合同步。证毕。

2 数值仿真

运用Matlab进行数值仿真,取时间步长τ=0.001 s,采用四阶龙格库塔法求解方程(1)和(3)。误差初始值为[e1,e2,e3]=[-5,4,-7],k=720,满足上述定理。图2 为同步误差曲线。当时间t接近4 s时,系统同步误差e1稳定并趋于原点;当时间t接近5 s时,系统同步误差e2稳定并趋于原点;当时间t接近3 s时,系统同步误差e3稳定并趋于原点。实验结果表明,3个系统同步误差可以随时间的变化稳定并趋于原点,Rossler系统实现单一状态变量耦合同步,证明了上述结论的有效性。

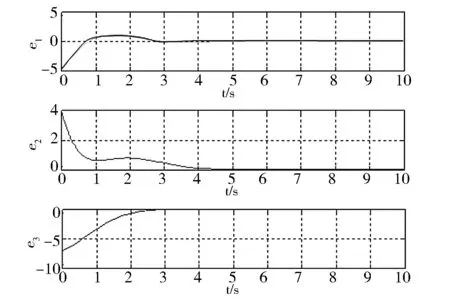
图2 采用耦合方法的同步误差图Fig.2 The synchronization errors with coupling method

3 结语

在混沌同步的控制方法中,耦合同步收敛的速度较快,但未知的耦合强度却难以确定。本文选取Rossler混沌系统为研究对象,从工程实际需要出发改进了单向耦合同步法,提出了单一状态变量耦合同步法,即对一个系统状态变量进行耦合;利用Routh-Hurwiz稳定性准则,经过数学理论推导得到了系统渐近稳定时耦合系数需要满足的充分条件,最终实现了Rossler混沌系统单一状态变量的耦合同步。最后数值仿真的结果证明了此方法的正确性和可行性。后续工作将以超混沌系统和分数阶混沌系统为研究对象,有效实现同步控制,以期提高鲁棒性和抗干扰能力,在实际工程中得到广泛的应用。