数值波浪水池中两栖武器摇荡运动研究

郝一凝，马新谋，苏红星，王常龙，段婉君

(1.中北大学 机电工程学院，山西 太原 030051；2.中国第一重型机械股份公司专项装备研究所，辽宁 大连 116113；3.重庆铁马工业集团有限公司，重庆 400030)

两栖武器在水上浮渡的过程中，由于受到波浪扰动，产生六自由度摇荡。两栖武器的摇荡运动会严重影响武器的水上性能、作战性能及舒适性能。因此，研究波浪载荷下两栖武器的摇荡运动对两栖武器的发展具有重要的意义[1]。

针对两栖武器摇荡运动的研究方法主要为理论计算法、拖模试验法、数值波浪水池法(Numerical Wave Tank，NWT).马新谋等[2-4]针对两栖战车横摇运动进行了深入研究，建立了两栖战车线性与非线性横摇动力学方程，并开发了两栖战车的水上性能分析软件，计算得到了两栖战车的GZ曲线，进而计算出两栖战车的横摇运动方程回复项系数。徐国英等[5-6]选择5种两栖战车进行研究，分析在3种风级下两栖战车的摇荡运动情况，通过试验得到两栖战车共振频率及无因次系数；并得到了增大阻尼系数来减小摇荡运动。目前，对两栖武器摇荡运动研究主要集中在理论计算与拖模试验，应用数值波浪水池方法对两栖武器摇摆运动进行数值仿真的研究尚未发现公开报导。

笔者基于Fluent软件，对两栖武器自由横摇运动进行数值仿真，并与拖模试验结果对比，验证数值仿真的准确性。采用明渠流造波技术及动网格技术，对波浪与两栖武器相互作用进行仿真计算，得到两栖武器的横摇、横荡、垂荡等水上运动响应，并研究不同波浪要素下对两栖武器摇荡运动的影响。仿真研究结果可以为两栖武器的设计优化提供一定的参考依据。

1 两栖武器自由横摇运动

1.1 自由横摇运动方程

两栖武器自由横摇运动过程是两栖武器由于偏离平衡点产生初始倾角，此时两栖武器存在初始的横倾力矩，在回复力矩和惯性力矩影响下，两栖武器绕平衡点往复运动。由于水的粘性特性产生阻尼作用，两栖武器的横摇运动幅度逐渐减小，直到其静止不动。

静水中两栖武器非线性自由横摇衰减运动可以用二阶常微分方程表示，即[7]：

(1)

1.2 拖模试验

拖模试验是研究两栖武器摇荡运动的重要手段。本拖模试验是根据两栖武器的实际尺寸按比例缩小制成，并在静水水池中进行横摇试验。该试验可得到两栖武器的固有周期以及作用于两栖武器上的水动力系数等。拖模试验的两栖武器模型根据某8×8轮式122 mm两栖武器外形尺寸建立，按照1∶4的比例设计试验模型。拖模模型实物如图1所示。

试验模型与两栖武器的主要参数如表1所示。

表1 试验模型与两栖武器主要参数

静水横摇试验是在长160 m、宽7 m、深3.7 m的水池中进行。试验前对模型经过加装拖点、配重、防水保护等必要的处理。对拖模进行静水自由横摇衰减试验，静水自由横摇衰减试验方法是将两栖武器倾斜一定角度后释放，监测两栖武器的运动响应，进而得到两栖武器的横摇周期与横摇角变化曲线，即自由横摇衰减曲线。

1.3 自由横摇运动仿真

数值水池长L=60 m，工作水深H=5 m.其边界条件上下面设为墙壁，左面设为速度入口，右面设为自由流动。两栖武器仿真计算模型简化为两栖武器二维最大横剖面。考虑软件的仿真计算效率，将两栖武器的轮胎及上装部分进行了简化处理，并忽略了空气阻力和两栖武器配件产生的其他影响。两栖武器吃水深为d=1.2 m，质心位置坐标为x1=31.063 m，y1=4.627 m.两栖武器在静水中的初始横摇角10°，之后在水池中做自由横摇运动。

进行自由横摇运动仿真的数值水池的网格划分采用静止区域结构网格与运动区域非结构网格混合形式。求解器设置为控制方程采用中心差分格式离散，采用SIMPLEC压力速度耦合算法，动量方程使用一阶迎风格式求解、采用PRESTO!格式离散Green-Gauss Node Based压力方程。将两栖武器设置为刚体，并设置动网格区域。两栖武器的自身质量、转动惯量通过二次开发的程序赋予到仿真软件中。通过在数值水池中的仿真计算得到两栖武器自由横摇衰减运动过程。

拖模试验结果与数值仿真结果对比图如图2所示。

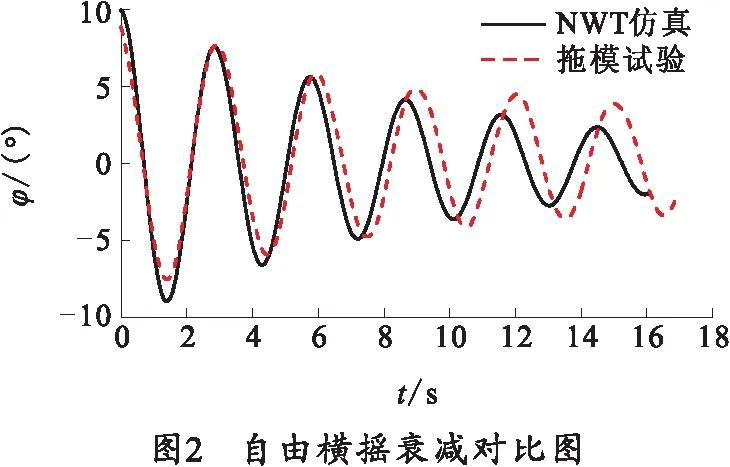
由图2可以看出两栖武器由初始状态释放后，在水的粘性作用下，横摇角度逐渐变小，并逐渐放缓运动，在数值水池中呈现了自由横摇衰减现象。通过软件仿真计算得到的两栖武器横摇周期为Ts=2.896 s，通过静水拖模试验得到的两栖武器横期为Te=2.998 s，两者的相对误差为3.52%.

从试验值与数值仿真的对比结果可以看出，数值仿真方法满足计算要求，适用于下文对于两栖武器的摇荡运动数值计算。

2 两栖武器摇荡运动

2.1 波浪理论

两栖武器在水上浮渡过程中，受到各类波浪作用。波浪分为线性波和非线性波。其中，在浮体计算领域最常用的是非线性的二阶Stokes波，其波面方程η和势函数φ[8]为：

(2)

(3)

取波长为λ=8 m，波高H=0.4 m，进行二阶Stokes波波面方程的理论计算。

2.2 数值波浪水池建立

采用明渠流造波技术对数值水池进行边界造波，在左端边界设置波浪模型Open Channel Wave BC，输入波长为λ=8 m，波高H=0.4 m.流体的湍流设置为SST模型。

为了进一步研究造波效果，对水池x=3 m处使用波高监测仪，并将监测波高数据与求解方程得到的理论数据进行比对。波形数据结果如图3所示。

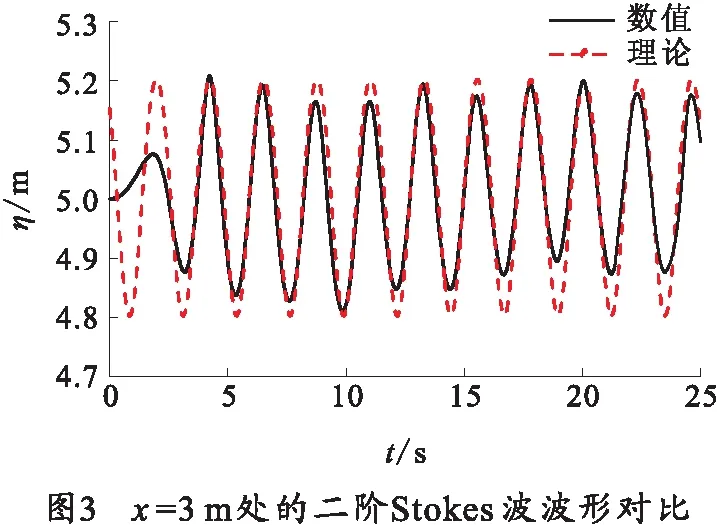
图3为水池3 m处的二阶Stokes波波形图,可以看出二阶Stokes波具有波峰尖锐波谷平缓的特点。数值波浪水池中二阶Stokes波计算结果如表2所示。

表2 二阶Stokes波计算结果

利用明渠流造波得到的波浪形态较为理想，与理论波形一致性较好。由于水存在粘性，波浪在传播过程会产生衰减效应。因此选取数值波浪水池的3～16 m为工作段，保证两栖火炮与波浪相互作用计算区域为最佳区域。

2.3 摇荡运动仿真

通过建立数值波浪水池及对二阶Stokes波自由液面的监测，得到波浪与两栖武器的最佳耦合区域。将两栖武器的计算模型放入该耦合区域，两栖武器的质心位置坐标为x2=11.063 m，y2=4.627 m,吃水深为d=1.2 m,取二阶Stokes波波长为λ=8 m，波高H=0.4 m，对两栖武器横摇、横荡、垂荡三自由度复合运动进行仿真。仿真计算得到t=15 s时刻两栖武器在自由液面中的状态,如图4所示。

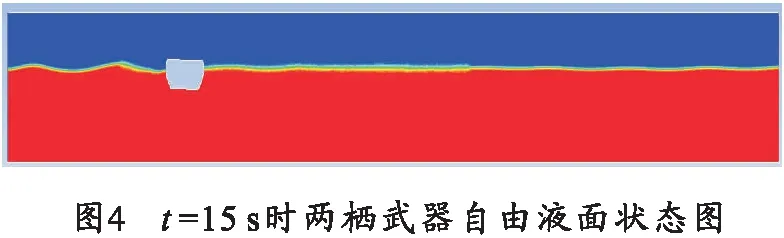
图4表示t=15 s时，两栖武器随波浪运动，两栖武器已从10 s的向左倾斜转向右倾斜，两栖武器继续被波浪向水池中间推。

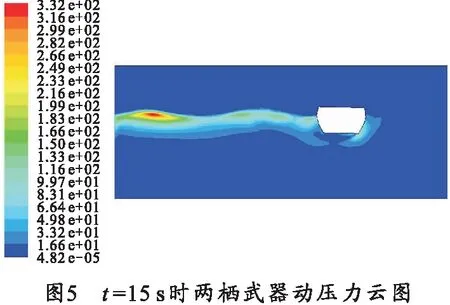
不同时刻两栖武器的动压力云图如图5所示。图5中两栖武器在自由液面上向右浮动倾斜，此时两栖武器的右端压力大于左端压力，右端平均压力主要集中于两栖武器的中部下部。产生的动压力差集中在液面与两栖武器附近。其中，自由液面的动压力差产生于数值波浪水池在造波过程中，波浪从水池左端向右端传播。因此可分析出，两栖武器在自由液面随波往复摇荡运动是由底部的压力变化导致的。

通过数值仿真计算得到波长为λ=8 m，波高H=0.4 m的二阶Stokes波作用下，两栖武器质心横摇、横荡、垂荡变化曲线。

图6为在0～20 s的时间段内，二阶Stokes波的扰动下，两栖武器的横摇变化曲线,即其沿纵轴转动的角度变化。横摇运动是由横向的惯性力矩、恢复力矩相互作用所产生的周期性往复运动。由于两栖武器位于的工作区距造波的左边界距有一定距离，波浪从左端面传到两栖武器附近,在t=5 s之后受到波浪的扰动，两栖武器开始大幅度的横摇运动。在波高为0.4 m，波长为8 m的二阶Stokes波扰动下，两栖武器的横摇角在-7.5°～7.5°之间成周期性变化，周期为2.5 s.

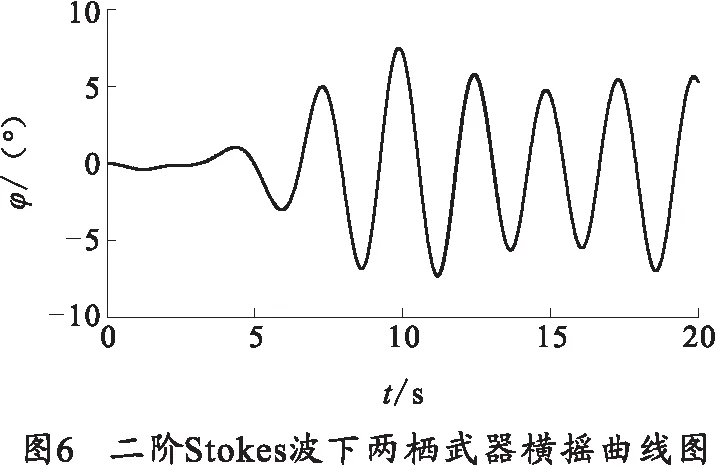
图7为在0～20 s的时间段内，二阶Stokes波的扰动下，两栖武器的横荡变化曲线。两栖武器的横荡运动表示其在水平方向的位移变化情况。两栖武器在波浪力的推动下，逐渐向水池右端面移动。在仿真计算的20 s内，两栖武器从左至右移动了4.3 m.

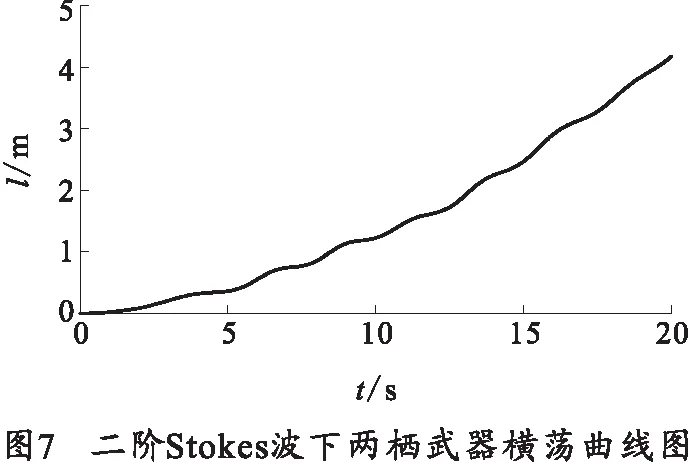
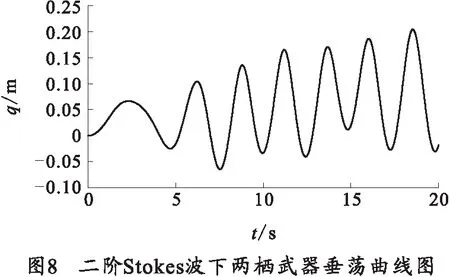
图8为在0～20 s的时间段内，二阶Stokes波的扰动下，两栖武器的垂荡变化曲线。两栖武器的垂荡运动表示其在竖直方向的位移变化情况。在浮力与竖直方向的运动惯性相互作用产生上下位移变化即垂荡运动。两栖武器垂荡呈往复性周期变化，其垂荡位移在-0.1～0.2 m之间。

3 影响因素分析

3.1 不同波高下的摇荡运动

具有波高、波长等不同要素的波浪对两栖武器的作用力也不同，因此两栖武器在水中会产生不同的运动响应。针对二维问题，分析不同波浪因素对两栖武器的横摇、横荡、垂荡三自由度复合运动响应。

取二阶Stokes波波长λ=8 m一定的情况下，不同波高H=0.2，0.4 m时作用下，对两栖武器的横摇、横荡、垂荡运动进行仿真计算。

不同波高的波浪作用下，两栖武器的横摇仿真结果如表3所示。

表3 不同波高作用下的两栖武器横摇结果

不同波高的作用下，两栖武器的横摇运动响应曲线如图9所示。从仿真结果可以看出，两种波高作用下，两栖武器的横摇运动都成往复运动。由表3可以得出，波高减小，横摇周期随之减少了7.1%，其中两栖武器最大横摇角减少了52.8%.因此，可得出较小的波高会降低两栖武器的横摇运动响应。

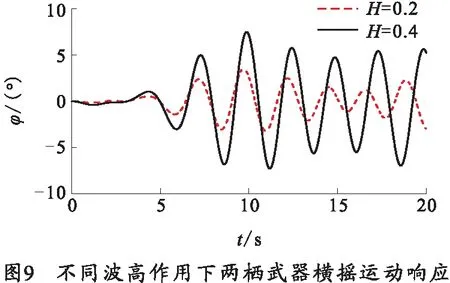
不同波高的作用下，两栖武器的横荡运动响应曲线如图10所示。

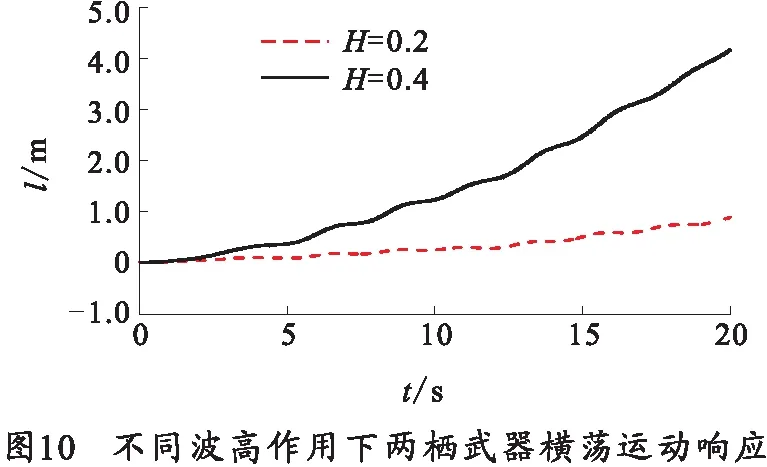
从图10可以看出，两栖武器的横荡位移都不同程度的增加。在波高0.4 m的波浪作用下两栖武器横荡位移为4.158 m；在波高0.2 m下两栖武器横荡位移为0.829 m.可得到结论，波高对两栖武器的横荡运动影响较大，波高越大横荡幅度越大。

不同波高的作用下，两栖武器的垂荡运动响应曲线如图11所示。不同波高的波浪作用下，两栖武器的垂荡仿真结果如表4所示。

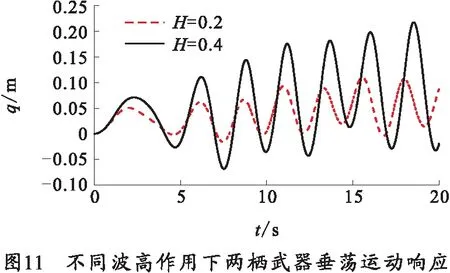
表4 不同波高作用下的两栖武器垂荡结果

波高H/m垂荡周期/s最大上升位移/m最大下沉位移/m0.22.4220.1100.0150.42.5170.2170.068

从图11可以看出，两种波高作用下，两栖武器的垂荡运动都呈现不同程度地往复升沉。波高减少，垂荡周期减少了3.8%，两栖武器的最大上升位移减少了49.31%，两栖武器的最大下沉位移减少了77.94%.因此，可得出较小的波高会降低两栖武器的垂荡运动响应。

上述计算分析可得，两栖武器的横摇、横荡、垂荡运动响应受到不同波高的影响，随波高的减小而减小。

3.2 不同波长下的摇荡运动

取二阶Stokes波波高H=0.4 m一定的情况下，波长λ=6，8 m的二阶Stokes波作用下，对两栖武器的横摇、横荡、垂荡运动进行仿真计算。

不同波长的波浪作用下，两栖武器的横摇仿真结果如表5所示。

表5 不同波长作用下两栖武器横摇结果

图12为不同波长作用下两栖武器横摇运动响应对比，从仿真结果可以看出，两种波长作用下，两栖武器的横摇运动同样做往复运动。根据表5的对比可以得出，波长的减小，会导致两栖武器横摇周期随之减小，其中两栖武器的最大横摇角减小了40.6%.因此可得，波长减小会降低两栖武器横摇运动响应。

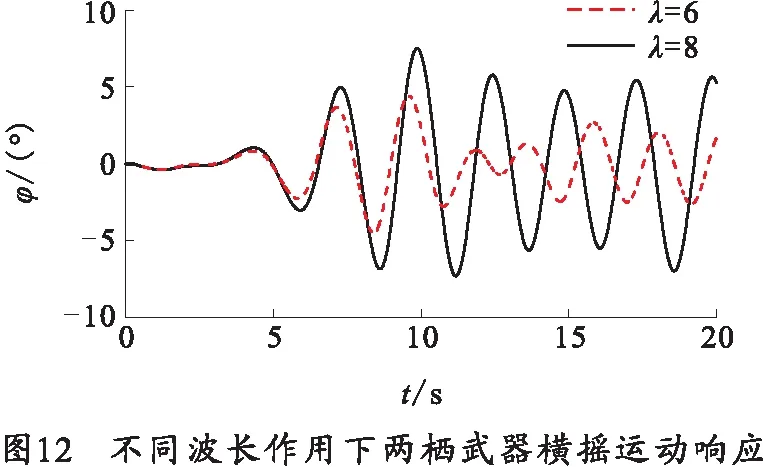
图13为不同波长作用下两栖武器横荡运动响应对比，从仿真结果可以看出，在0～20 s内，两栖武器不断向水池右端移动。但根据仿真结果可知，两栖武器在波长6 m下的横荡位移为4.158 m，在波长8 m下的横荡距位移为4.322 m，表明波长的减小对两栖武器横荡运动影响不大。

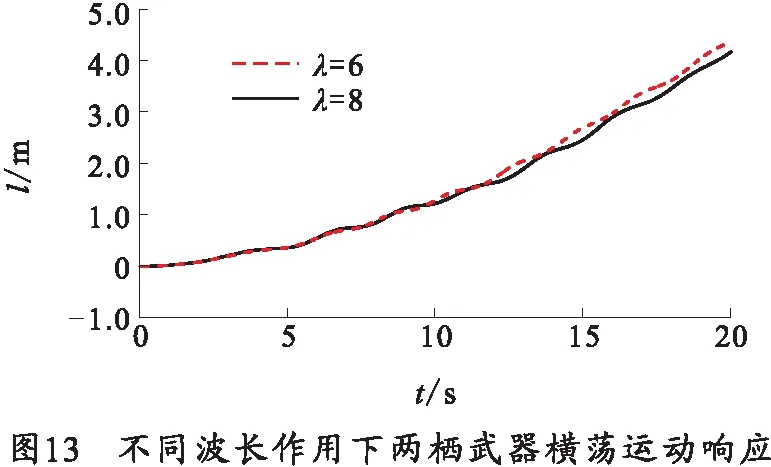
不同波长的波浪作用下，两栖武器的垂荡仿真结果如表6、图14所示。

表6 两种波长的波浪作用下垂荡结果

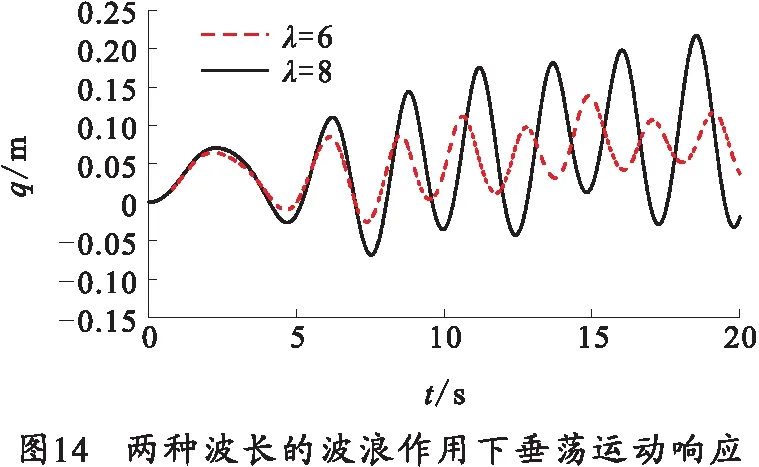
从表6、图14可以看出在不同波长条件下，两栖武器的垂荡运动往复升沉。波长减小，垂荡周期随之减小，两栖武器的最大上升位移减小了36.41%，两栖武器的最大下沉位移减小了63.24%.波长的减小有效降低了两栖武器的升沉。

通过对不同波长的波浪作用下两栖武器横摇、横荡、垂荡运动仿真计算，随着波长的减小，两栖武器的横摇、垂荡运动响应减小，波长对两栖武器的横荡运动影响较小。

4 结束语

通过对两栖武器的静水横摇拖模试验、自由横摇运动数值仿真及在数值波浪水池的两栖武器摇荡运动仿真计算，可以得到以下结论：两栖武器的自由横摇运动呈规律衰减，数值仿真结果与拖模试验吻合较好。通过数值波浪水池法计算了两栖武器在波长为λ=8 m，波高H=0.4 m的二阶Stokes波作用下的摇荡运动响应；并分析了在不同波长、波高作用下两栖武器的摇荡运动。在波长不变的情况下，两栖武器摇荡运动随波高的增加而增加；在波高不变的情况下，两栖武器横摇与垂荡，随波长增加而增加，但波长对横荡运动影响不大。综上所述，数值波浪水池法可以作为一种研究两栖武器水上性能的方法，具有一定的参考价值。