初始孔隙率对高放射性废物处置库缓冲材料性状的影响
2019-09-20秦爱芳
秦爱芳, 贾 旭
(上海大学土木工程系, 上海200444)
近年来, 核能作为世界公认的清洁能源得到了充分的开发和使用. 与此同时, 安全、有效地处置高放射性核废料也是世界各国面临的一项重大课题. 目前, 在众多方案中, 地质处置[1]是一项被普遍接受的方案.
高放射性核废料处置库(high-level radioactive nuclear waste repsitory, HLWR)通常由废物罐、玻璃固化体、缓冲材料、回填材料和围岩组成. HLWR 关闭运行后, 通常需要长达千年甚至万年以上处置期限. HLWR 封闭运行后高放射性废料产生的热量以及地下水压产生的高静水压力, 会使废物罐和围岩之间的缓冲材料(主要为膨润土)产生很复杂的热-水-力(thermohydro-mechanical, THM)耦合作用. HLWR 中缓冲材料的选择对整个处置库是否能够安全、可靠地运行至关重要.
目前, 许多欧美国家使用膨润土作为HLWR 的缓冲材料, 利用膨润土的低渗透性、膨胀性、充足的导热性和高交换性[2]来防止核泄漏. 中国拟采用GMZ 膨润土作为缓冲材料, 同时选择北山花岗岩作为围岩. GMZ 膨润土除了具有高膨胀性和导热性以外, 其高阳离子交换能力和高蒙脱石含量会进一步阻止核泄漏的发生[3].
Villar[4]和Komine[5]预测了不同孔隙率下饱和膨润土的渗透系数变化曲线. Olivella等[6]和Gens 等[7]将高放射性处置库周围的FEBEX 膨润土孔隙率分为两部分: 宏观孔隙部分和微观孔隙部分, 并利用数值模拟分析了处置库在侧限条件下的饱和度、应力、温度变化情况.叶为民等[8]、刘月妙等[9]、张玉军等[10]、孙德安等[11]也对GMZ 膨润土的导热性、力学特性、水力学特性、微观孔隙特性等进行了研究. 宋杰等[12]探究了压实度对非饱和土电阻率的影响.Ye 等[13-14]和Tang 等[15]研究了GMZ 膨润土中, 温度对吸力和液体渗透系数的影响.
膨润土压实度的不同, 会造成不同的初始孔隙率, 进而影响HLWR 关闭运行后吸力、饱和度、渗透系数、应力、温度等的变化. 若初始孔隙率太小, 可能会造成HLWR 关闭运行后内部压力过大, 侧限条件下可能会对围岩或开挖扰动区产生较大应力和应变, 致使围岩开裂, 核素随着地下水外泄等情况. 若初始孔隙率过大, 膨润土无法起到缓冲和回填材料的作用, 可能会造成HLWR 关闭运行后膨润土很难膨胀密实, 膨润土和围岩之间产生缝隙[16].
HLWR 作为各个国家的重大安全工程, 对人民生活和国家安全有着重要影响. 我国核废料处置库研究正处于初步阶段, 大多针对缓冲材料GMZ 膨润土的水-土特性和围岩的水、力学特性展开, 处置库现场试验也在准备阶段. 因此, 考虑我国高庙子膨润土特性, 建立一套合理可行的数值模拟, 用来预测或反映处置库不同条件下的运行情况至关重要.
1 THM 三相耦合机理
当HLWR 封闭之后, 膨润土将接收由废物罐不断散发出的热量, 使其温度升高. 同时, 地下水在水压的驱动下不断向膨润土内渗透, 使膨润土内的水压和饱和度产生变化. 膨润土内的温度和饱和度发生改变后, 自身应力也会产生复杂的变化. 在热、水、力三相相互作用下, 膨润土内部就产生了一个非常复杂的THM 耦合现象. 例如, 距离废物罐较近的膨润土内的水分受热后将蒸发成水蒸气, 该处的膨润土由于失去水分使得土内孔隙变小, 远处的水分更难以渗透, 其饱和度及水压力减小. 同时, 该处的膨润土温度较高, 又会产生较高的温度应力.
HLWR 中除了THM 耦合机理复杂外, THM 耦合作用的时间也较长. HLWR 内部储存的高放射性核废料含有众多放射性元素, 如铯、铀、钋等都拥有数以万年计的半衰期, 故HLWR中的THM 耦合会持续几千年甚至几万年.
2 本构方程
本工作中的热、水本构方程均引自文献[7].
2.1 热本构方程
热传导假定服从Fourier 定律:

式中, ic为介质传导热通量, ▽T 为介质温度的微分, λ 为介质综合热传导系数(与土热传导系数λs、水热传导系数λl、孔隙率以及饱和度有关), 其关系式为

其中sl为膨润土的饱和度, λsat为膨润土完全饱和时的热传导系数, λdry为膨润土干燥情况下的热传导系数.
2.2 流体本构方程
孔隙中液相遵循Darcy 流动定律, 即

式中: ql为液相的流量; Kl为液相渗透系数张量, 且Kl= KrlK/µl, 其中Krl为液相相对渗透系数, µl为液相的动力黏滞系数; g 为重力向量; K 为介质固有渗透系数; ▽pl为水压力的微分; rl为液相的密度.
以上计算采用的几个关系式如下.
(1) 固有渗透系数K 和孔隙率相关, 采用Kozeny 模型, 即
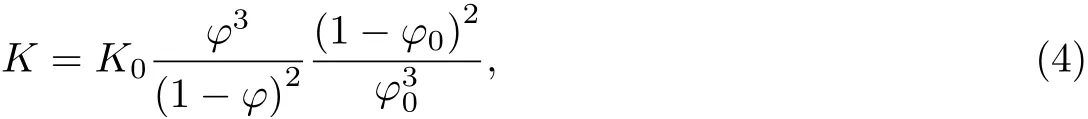
式中, φ0为初始孔隙率, K0为φ0时的固有渗透系数.
(2) 非饱和土的液相相对渗透系数Krl与其饱和度密切相关, 即

式中: A 通常为1; n 为指数, 通常取2~4; Se为有效饱和度. Se与实际饱和度Sl之间的关系如下:

式中, Slr为液体剩余饱和度, Sls为液相最大饱和度.
(3) 为了反映饱和度与基质吸力之间的关系, 采用比较常用的Van Genuchten 模型, 即

式中, p=P0σ/σ0, 其中P0为参照温度下的进气值, σ0为参照温度下的表面张力, σ 和p 为计算温度下的表面张力和进气值, m 为形状参数.
2.3 力学本构方程
非饱和土的应力应变本构模型非常复杂. 本工作采用巴塞罗那基本模型(Barcelona basic model, BBM). BBM 模型是在修正的剑桥模型基础上, 由Alonso 等[17]进一步修改完成的非饱和土弹塑性本构模型. BBM 模型中选用两个屈服面, 考虑了吸力的影响, 并假定吸力增加会提高非饱和土的黏聚力但仍保持内摩擦角为常数. BBM 模型体积应变的计算关系式为
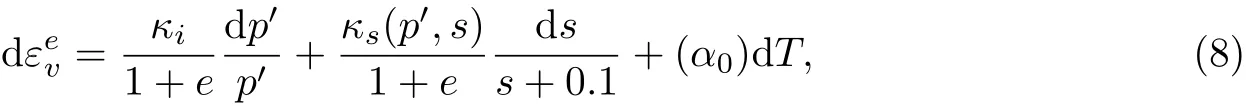
式中,

其中κi0是初始零吸力时的平均应力, κs0为初始吸力值, αi和αsp为试验参数, α0为弹性热应变的试验参数, Tref为初始温度, dT 为温度的变化量.
BBM 模型采用双屈服面模型. 屈服面1 为
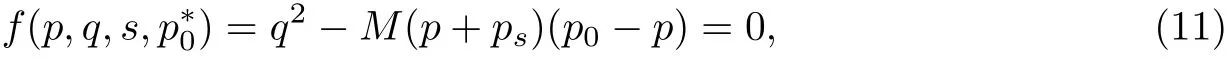
式中, p=(σ1+2σ3)/3-pa, q =σ1-σ3, M 为饱和土临界状态线的切线值,
式中:CM为测量成本;CZ为测量误差成本;CMF为测量仪器成本;CMM为测量策略成本;CEA为弃真误差成本;CEB为纳伪误差成本;CEA为单个弃真事件成本;cEB为单个纳伪事件成本;N为待测区域关键部位的个数;P(∪TfA)为公差T时弃真事件发生的概率;P(∪TfB)为公差T时纳伪事件发生的概率。

pc为一参照应力, p*0为土饱和状态下的前期固结压力, p0为对应于吸力s 情况下的前期固结压力, λ(0)为饱和状态下土ν-ln p 坐标体系中的原始压缩曲线斜率, λ(s)为吸力为s 情况下土在ν-ln p 坐标体系中的原始压缩曲线斜率, β 为控制λ(s)随吸力增长速率的参数, k 为因吸力导致张力变化的参数.
屈服面2 为

式中, s0是土体受到的前期最大吸力. 当吸力从s0过渡到0 时, 土体也将从弹性状态转变到弹塑性状态.
2.4 平衡方程

(1) 水的质量平衡方程为式中, θwl和θwg分别为单位体积中液相中和气相中水的质量, φ 为孔隙率, Sl和Sg分别代表液相和气相的饱和度, Jwl和Jwg分别代表水在液相和气相中的总质量通量, fw为外部水源供应量.
(2) 空气的质量守恒方程为
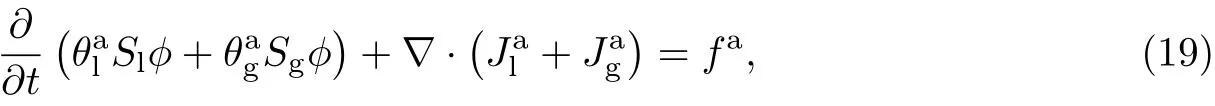
式中, θal和θag分别表示单位体积液相和气相中空气的质量, fa为单位体积介质中外界提供空气的质量, Jal和Jag分别表示液相和气相中空气流动的质量(相对于固定参照系).
(3) 在多项耦合条件下有多种物质存在, 考虑到在非饱和土中有多种物质转移, 故采用如下能量平衡方程:

(4) 忽略惯性力的静力平衡方程为

式中, σ 为应力状态向量, B 为体力向量.
对于饱和多孔介质, 力学本构方程引入有效应力概念, 即

式中, MT= (1,1,1,0,0,0). 但对于非饱和多孔介质的本构方程, 通常引入两个独立的应力状态量, 即净法向应力σ-pgM 以及基质吸力s=pg-pl, 其中pg为气压力, pl为水压力.
3 数值分析算例
本算例采用西班牙ENRESA 在瑞士核废料地下试验室进行的核废料处置库模型, 如图1所示. 本试验在地下约500 m 的岩层中开挖一个水平的直径为2.4 m、长为18.8 m 的坑道作为处置库; 沿水平轴向放置两个半径为0.45 m、长为4.54 m 的废物罐; 废物罐周围用缓冲材料GMZ01 膨润土填充. 轴对称计算模型如图1(c) 所示, 其中CL 表示中心线, CL 右侧分别为热源、GMZ01 膨润土、花岗岩, 在GMZ01 膨润土的左侧为铜罐, 即热源、边界条件和初始条件如下: GMZ01 膨润土的初始温度为20◦C, 初始各向应力为0.5 MPa, 初始吸力为90 MPa,初始饱和度为0.46, 初始孔隙率分别取0.3, 0.4, 0.5, 大气压恒为0.1 MPa; 花岗岩的初始温度为20◦C, 初始各向应力为28 MPa, 地下埋深为500 m, 初始水压为0.5 MPa, 初始孔隙率为0.01, 边界始终保持0.5 MPa 的水压, 用来模拟地下水不断向围岩GMZ01 和膨润土补充水分.GMZ01 膨润土的基本参数如表1[18]所示. 本工作采用的基本控制方程为式(18) ~(21).
模型的热、力学边界条件如下: 左边界在水平方向加约束, 上、下边界在垂直方向加约束,右边界在水平方向施加横向水平压力; 热源从第一天开始, 不断加热, 第21 天时温度达到100◦C, 保持100◦C 至第1 095 天.
为了监测模型中温度、饱和度、孔隙率、应力、吸力等变化情况, 在径向设定了2 个监测点(见图2) , 其中a 点距离热源中心0.57 m, b 点距离热源中心1.02 m(靠近花岗岩处). 该计算模型有180 个单元, 273 个节点. 图2 显示了计算结果输出点和单元的位置.

表1 主要计算参数Table 1 Main computation parameters

图1 HLWR 原位试验模型Fig.1 In situ test model of HLWR
4 计算结果与分析
4.1 温度的变化
本工作研究了不同孔隙率(φ = 0.3, 0.4, 0.5)情况下温度、饱和度、应力等的变化. 根据表1 的参数, φ=0.3 的GMZ01 膨润土干密度为1.995 g/cm3, φ=0.4 的GMZ01 膨润土干密度为1.710 g/cm3, φ=0.5 的GMZ01 膨润土干密度为1.425 g/cm3.

图2 计算结果输出点和单元的位置(m)Fig.2 Position of point and unit of calculating output
图3(a)和(b)为图2 中a, b 两点第21 天到第1 095 天的温度变化曲线. 可以看出, 靠近花岗岩处的GMZ01 膨润土初始孔隙率越小, 温度就越高, 这是因为干密度越大导热系数越大,接收的热量就越快. 当干密度大于1.4 g/cm3时, 比热容随干密度的增加略有减小[8]. 这意味着初始孔隙率越小, 接收的热量越多; 比热容越小, 温度越高. 靠近花岗岩处, 温度变化相差虽然不大, 但是干密度越大, 热扩散系数越大[8], 所以在靠近花岗岩处的GMZ01 膨润土初始孔隙率越小, 温度也略高.

图3 a, b 两点GMZ01 膨润土温度随时间变化曲线Fig.3 Variation curves of GMZ01 bentonite temperature with time at a and b points
4.2 饱和度和吸力的变化
图4(a)为不同初始孔隙率膨润土在a 点的饱和度随时间变化曲线. 可以看出, a 点处GMZ01 膨润土的饱和度先减小, 随着时间的增长略有升高. 因为在靠近热源处温度较高,GMZ01 膨润土在热源加热下, 水分蒸发, 饱和度随之降低. 之后由于岩石水分的不断补充, 再次使饱和度上升. 孔隙率较低的GMZ01 膨润土, 渗透系数较小, 水分更难渗透进来, 使得a 点处的饱和度出现了孔隙率越小饱和度越小的现象.
图4(b)为不同初始孔隙率GMZ01 膨润土在b 点的饱和度随时间变化曲线. 可以看出, b点处GMZ01 膨润土的饱和度总体随时间呈上升趋势. GMZ01 膨润土中靠近花岗岩处的水分主要来自于两个部分: 一部分来自于靠近热源处的水分蒸发形成的水蒸气的迁移; 另一部分来自于围岩水分的渗透. 这两个来源使得靠近花岗岩处的GMZ01 膨润土的饱和度不断上升. 由图4(a)和(b)可以看出来, 不同的初始孔隙率在a, b 两点表现出的规律是相反的. 在靠近热源处, 初始孔隙率越大饱和度越大; 在靠近花岗岩处, 初始孔隙率越大饱和度越小. 由于热源相同, 不同孔隙率的GMZ01 膨润土的初始饱和度相同, 蒸发的水分是等量的. 在a 点, 孔隙率越小的GMZ01 膨润土则饱和度降低得越多; 当迁移至b 点, 孔隙率较小的GMZ01 膨润土更加容易饱和.
图4(c)和(d)为不同初始孔隙率GMZ01 膨润土在a, b 两点的吸力随时间变化曲线. 可见:a 点GMZ01 膨润土的吸力随时间先增加后减小, 而b 点GMZ01 膨润土的吸力是不断减小的;靠近热源处的吸力随初始孔隙率的增大而减小, 而靠近花岗岩处的吸力随初始孔隙率的增大而增大. 吸力和饱和度的关系是紧密相连的, 饱和度越大则吸力越小, 反之, 饱和度越小则吸力越大. 这也和饱和度的变化规律相互印证.
根据已有的对GMZ01 膨润土吸力和渗透系数的研究可知: 当吸力大于65 MPa 时, 水的渗透系数随吸力的增大而增大; 当吸力小于60 MPa 时, 渗透系数随吸力的增大而减小; 当吸力小于20 MPa 时, 渗透系数随吸力的增大而减小的幅度会更大[12]. 由图4(c)和(d)可以看出:靠近热源的GMZ01 膨润土处于高吸力状态下, 该点附近GMZ01 膨润土的渗透系数随吸力的增大而增大, 所以该点GMZ01 膨润土的渗透系数随着初始孔隙率的增大而减小; 靠近花岗岩处GMZ01 膨润土的吸力大部分小于60 MPa, 所以该处的渗透系数随着吸力的增加而减小,即渗透系数随着初始孔隙率的增大而减小. 这也是造成图4(a)和(b)饱和度情况的原因之一.
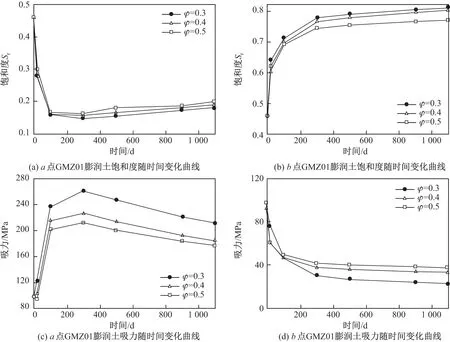
图4 a, b 两点GMZ01 膨润土饱和度和吸力随时间变化曲线Fig.4 Variation curves of GMZ01 bentonite saturation and suction with time at a and b points
4.3 应力的变化
图5(a)和(b)为不同初始孔隙率的GMZ01 膨润土在第21 天和第1 095 天的径向应力随距离的变化关系. 可以看出: 第21 天时不同初始孔隙率的GMZ01 膨润土的应力变化不大; 靠近废物罐和靠近花岗岩处的GMZ01 膨润土应力较大, 中间部分的应力较小. GMZ01 膨润土应力的增加, 主要与两个因素有关: 一是由于饱和度的增加会导致GMZ01 膨润土内蒙脱石吸水,发生水化作用并迅速产生膨胀; 二是来自于热源产生的热应力, 在靠近废物罐处的GMZ01 膨润土除了因水膨胀以外, 还受到来自于废物罐的热应力. 在靠近花岗岩处的GMZ01 膨润土受到的热应力虽然较小, 但由于饱和度较高会产生较大的膨胀应力. 靠近废物罐处的GMZ01 膨润土初始孔隙率越大, 温度越低, 热应力越小; 靠近花岗岩处的GMZ01 膨润土初始孔隙率越大, 饱和度越低, 膨胀应力越低, 所以GMZ01 膨润土的应力随着初始孔隙率的增加而减小.

图5 第21 天和第1 095 天时径向应力随距离的变化关系Fig.5 Variation curves of stress with distance in the 21st and 1 095th days
4.4 数据验证
图6 为THM 耦合, 初始孔隙率为0.4 时, 距离热源0.465, 0.8, 1.135 m 的c, d, e 处的饱和度计算结果以及与Gens 等[7]的结果对比. 可以看出, 二者的饱和度变化规律相同, 结果相似,从而验证了本方法的合理性.
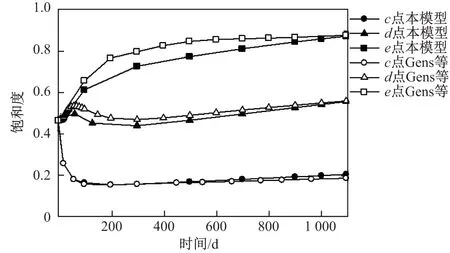
图6 饱和度曲线对比结果Fig.6 Comparisions of the saturation curves
5 结 论
本工作通过有限元软件Code-Bright 进行数值模拟, 研究了不同初始孔隙率下的温度、饱和度、吸力、应力的变化规律, 并得到以下结论.
(1) 就HLWR 内GMZ01 膨润土温度场而言, 初始孔隙率或压实度的不同会对靠近热源处GMZ01 膨润土的温度产生明显变化. 在靠近热源处, GMZ01 膨润土内温度随初始孔隙率的减小而增大; 在靠近花岗岩处, 温度随初始孔隙率的变化不大.
(2) 就HLWR 内GMZ01 膨润土渗流场而言, 初始孔隙率的不同会导致明显的渗流场变化. 在靠近热源处, 初始孔隙率越大的GMZ01 膨润土其饱和度越大, 吸力越小; 在靠近花岗岩处, 初始孔隙率越大的GMZ01 膨润土其饱和度越小, 吸力越大.
(3) 就HLWR 内GMZ01 膨润土应力而言, 初始孔隙率不同会造成应力有较大不同. 第21天, 不同的初始孔隙率, 应力变化较小; 第1 095 天, 初始孔隙率越大, 应力越小.
