面板有序响应模型多种参数估计方法的仿真比较

陈永伟，庄佳强

(1.浙江工商大学 经济学院，浙江 杭州 310018；2.中南财经政法大学 财政税务学院，湖北 武汉 430073)

一、引言及文献综述

在应用研究中，我们经常会涉及到需要去分析一些个体的主观评价及其影响因素的作用机制问题。典型的例子包括居民对自身幸福感(生活满意度)的主观评价、对宏观经济稳定性程度的判断、对企业债券的信用评级以及金融分析师对备选股票的推荐顺序等[1-4]。但是，在这些问题的主观评价中，个体异质性常常会发挥重要的作用。两个外在条件基本相似的个体会因为对生活采取积极或消极偏好的不同，而对自身的生活满意度评价出现较明显的差异。因此，为了获得研究结果的可靠结论，在计量方法上能够包含个体异质性的面板有序响应模型在这类问题的研究中就呈现出优势，也得到了广泛使用。同时，应用研究的需求本身也引起计量经济学家对面板有序响应模型参数估计方法的深入讨论。到目前为止，现存文献有关该模型的参数估计至少存在DvS、BUC、OMD和CML等多种方法[5-7]。那么，对于应用研究者而言，这些可供选择的估计方法有无差异？研究者应该使用哪种方法来获得所关心问题的稳健估计结果？本文希望通过蒙特卡罗仿真实验技术，通过比较各种主要方法在有限样本以及大样本条件下参数估计以及基于参数估计过程在后续假设检验阶段的表现结果，从而为实际应用研究者在方法论的选择上提供建议。

从计量方法来看，当我们感兴趣的结果变量具有排序结构时，如在满意度评价中，我们常用序数1、2、3、4、5来表示评价结果非常不满意、不太满意、一般、比较满意和非常满意的等级差异，这时的模型参数估计会存在特殊困难。这种困难主要表现在两个方面：一是极大似然方法会成为估计有序变量模型的主要方法，但是由于似然函数通常是待估计参数的非线性形式，因此很难直接给出待估参数的具体解析表达式，这也意味着在计算上，需要使用重复迭代直至收敛的算法(如牛顿方法)来获得模型参数的最终估计结果。现存文献中也有部分研究为了避免这种参数估计的复杂性，同时也为了获得参数估计结果在均值意义上的直观经济含义，采用传统的回归方法，将有序结果变量看成是普通的连续型随机变量，使用普通最小二乘法来估计模型参数[8-9]。这种处理方法的缺点是忽视了有序响应变量模型所能特定揭示出的事件发生概率的经济含义。二是在影响评价结果的机制分析中，为了包容个体异质性对评价结果产生的差异化影响，同时考虑到这种异质性也有可能与模型中的其他解释变量存在相关性，构建固定效应面板有序响应模型是现阶段研究所采用的主要方法，但同时这也给模型参数估计带来较大困难，主要原因是在固定效应中，反映个体异质性的参数会随着个体数量而增加，由此导致使用极大似然方法并不能获得模型参数的一致估计结果，这即是面板模型中的冗余参数问题[10]。Greene指出，在时间较短的面板中，因冗余参数导致的估计偏误会非常明显[11]。现有文献也有部分研究假定个体异质性与模型中的解释变量服从已知的特定相关关系，在这一约束下可以将固定效应面板有序响应模型转化为相对容易估计的随机效应结构形式[12]。Jansen提出了随机效应面板有序响应模型的极大似然参数估计理论[13]。

对于个体异质性与模型中的解释变量服从未知的相关性结构时，Das和van Soest提出，可以首先将有序结果变量的多种类别划分成两种类别[5]。例如，将满意度评价中的非常不满意、不太满意、一般、比较满意、非常满意五种类别合并成不太满意及以下、一般及以上两种类别，这样可以将面板有序响应模型转换为面板二元选择模型，进而通过构造面板二元选择模型的充分统计量，使用条件极大似然方法估计模型参数。由于充分统计量不依赖于反映个体异质性的参数，因此这种方法可以获得模型参数的一致估计结果。并且，由于对有序结果变量的类型划分存在多种不同的方式(如也可以将满意度评价划分为一般及以下、比较满意及以上两种类型)，相应地，每一种划分都对应于一套不同的参数估计结果，Das和van Soest建议使用最小距离方法将所有不同结果合并成最终的参数估计结果(本文简记这种方法为DvS估计)[5]。与DvS方法不同，Baetschmann等认为，既然每一种划分都是对真实参数的估计，那么在每一种划分下估计的参数结果就应该相等，因此他们建议使用受约束的条件极大似然方法来获得模型参数的一致估计结果(本文简记这种方法为BUC估计)[6]。Muris指出，在将有序结果变量转化为二元选择变量的过程中，除了可以按照上述方法进行划分之外，也可以补充使用其他方法进行划分，例如，对于样本第一期的观测值，按照评价等级是否高于“不太满意”而划分为二元选择变量，对于第二期观测值则按照评价等级是否高于“比较满意”而划分为二元选择变量，这样可以更多地利用有序结果变量的信息，从而在理论上也可以获得更有效的参数估计结果(本文简记这种方法为OMD估计)[7]。但是，当样本较小时，Muris也提出，我们并不需要使用最小距离法将针对每种划分下所获得的参数估计合成最终的一致估计结果，而是只需要将各种划分下的似然函数进行简单相加，然后使用一次条件极大似然的方法来获得参数的最终估计，这样可以避免在使用最小距离法过程中因计算维度过高的海塞矩阵而产生估计偏误(本文简记这种方法为CML估计)[7]。

那么，以上这些在理论上均能获得一致估计的方法在实际应用中有无差异？特别地，那些在渐近理论上更加有效的估计方法在后续的假设检验阶段是否也具有更明显的优势？鉴于个体异质性与模型解释变量存在未知的相关性结构这种设定形式在实际应用中更具有普遍性及广泛的使用价值，因此本文旨在使用蒙特卡罗仿真实验技术，通过比较DvS、BUC、OMD和CML四种方法在有限样本及大样本条件下参数估计与假设检验的表现，从而为实证研究的方法论选择提供建议。本文研究具有较明显的理论及实践指导意义，特别是，在面板有序响应模型的研究中，Ferrer-i-Carbonell和Frijters被发现提出了一种错误的条件极大似然估计方法[14]，在后续研究中却被广泛使用[15-16]，由此就更加突出了本文研究工作具有必要性及其重要意义，因此也体现了研究的贡献性。

二、面板有序响应模型设定及其四种主要估计方法

(一)模型设定

对于具有一般形式的面板有序响应模型，可以将其设定为：

(1)

(2)

(3)

其中，(τ0，τ1，…，τJ)被称为切点参数，并且τ0和τJ通常被标准化为-和+。模型(1)、(2)及(3)因此构成了固定效应面板有序响应模型。在有关主观评价的应用研究中，潜在变量经常被解释为个体i在时期t所获得的经济效用，yit是依据所获得的效用水平给出的评价等级[17]。因此，对于给定的个体异质性αi及解释变量xit，观察到评价结果yit=j的概率可以表示为：

P(yit=j|xit，αi)

(4)

相应地，模型的整体似然函数可以表示为：

(5)

其中，I(yit=j)是示性函数：若yit=j，则I(yit=j)=1；否则，I(yit=j)=0。根据式(5)给出的似然函数可以看出，当样本内T相对较小而N趋向无穷时，模型待估参数αi的数量会随着样本而增加，这即是面板模型中的冗余参数问题，由此也意味着即使从渐近理论上看，使用极大似然方法也不能获得模型参数的一致估计量。

(二)DvS估计方法

(6)

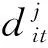
(7)

因此，基于式(6)给出的充分统计量，我们可以构造模型的条件对数似然函数形式：

(8)

(9)

(三)BUC估计方法

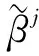
(10)

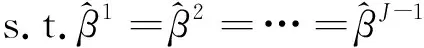
(四)OMD估计方法

di，π={di，t，π=I(yit≤π(t))，t=1，2，…，T}

(11)

(12)

(13)

需要注意的是，在将有序响应变量转换为二元选择变量时，针对我们给出的第一种方法(按照时不变的规则)转换有序变量，例如对于任意时间t，均令π(t)=π(1)，那么此时有∑t(ht-dt)τπ(1)=0。基于这一特征，上述充分统计量式(12)可以进一步表示为：

pi，π(d|β，τ)=

(14)

(15)

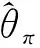
(16)

(17)

(五)CML估计方法

(18)

这种简洁的估计方法被称为是CML估计。

三、四种估计方法的仿真结果比较

为了比较DvS、BUC、OMD及CML四种估计方法在小样本以及大样本条件下的真实表现，本文设定统一的面板有序响应模型及其数据生成过程，并在这一相同的数据生成过程下综合比较以上四种方法在模型参数估计和假设检验两个阶段的表现结果。

(一)数据生成过程

假设面板有序响应模型的样本数据按照如下方式生成：

(19)

(20)

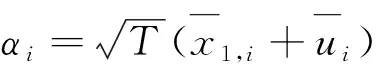
本文设定的面板有序响应模型具有一般的结构形式，与普通的有序响应模型或logit模型相比，若本文设定的模型没有包含面板数据结构，那么模型(19)、(20)首先会退化成有序响应模型形式。但是，由于有序响应模型通常被应用于主观评价问题的分析，而在这些问题中，个体异质性会对评价结果产生重要影响，因此从这个意义上看，面板有序响应模型具有更好的应用针对性。进一步，若本文设定的模型没有包含面板数据结构并且可观察变量yit的结果只有两种类型，那么此时面板有序响应模型可退化为logit模型的形式。

针对面板有序响应模型，现有参数估计方法及其渐近理论的推导都是基于T固定而N趋向无穷的条件，因此在数据生成中，我们设定N=100，200，500来模拟小样本的条件，设定N=1 000，2 000，5 000来模拟大样本的条件。在样本不断增大的条件下，T的取值都相对固定。我们将重点分析在每一种样本条件下，以上四种参数估计方法对系数β1和β2的估计，以及基于估计结果在假设检验阶段的不同表现。考虑到每次仿真生成样本数据并使用上述四种方法估计模型都需要耗费大量时间，因此在重复生成数据并估计模型时，我们将重复实验的次数设定为100次。

(二)参数估计的仿真结果比较

表1报告了当样本较小时，基于100次重复实验估计的系数β1和β2的均值，同时也报告了参数估计值对真实值的标准偏差，列于表中括号内。从整体上来看，即使在样本较小的条件下，使用BUC、CML和DvS方法获得的参数估计值与真实值都表现出较好的接近程度，估计结果具有准确性。相对而言，由OMD方法获得的估计值与真实值存在较大的偏差。这也说明，虽然从渐近理论的角度看，OMD方法更充分地利用了有序响应变量类别的信息，在理论上可以获得更有效的估计结果，但是当样本较小时，由于OMD方法首先需要估计模型(J-1)T次，然后在第二阶段使用最小距离估计时至少需要构造(J-1)T维的方差加权矩阵，当(J-1)T在数值上接近或超过N时，由OMD方法获得的估计结果就表现较差。

表1 小样本条件下的参数估计结果

从表中估计结果的具体比较来看，在纵向上，当T固定，如T=4，且N=100时，使用BUC、CML、DvS、OMD四种估计方法都会出现程度不同的估计偏误，相对而言，DvS的估计结果表现要优于其他三种方法。而当样本从N=100增加到N=500时，上述四种方法的估计值都会出现向真实值逐渐靠近的趋势，这一现象说明，四种估计方法都存在收敛性的特征。具体来看，当N=500时，我们发现，由BUC、CML和DvS三种方法获得的估计结果与真实值已经足够接近，而由OMD方法获得的估计值表现较差，这也说明OMD方法在收敛速度上可能略慢于其他方法。从估计结果的横向比较上看，当N固定，如N=100时，随着时间T变化，由BUC、CML和DvS三种方法获得的估计结果没有表现出明显的趋势，但是由OMD方法获得的估计结果在T增加时会逐渐恶化，主要原因在于，OMD方法依赖于时间T的变化，因为在T增加时，参数估计中需要构造的方差加权矩阵的维数(J-1)T会快速增加，因此在小样本下，OMD方法并没有产生较好的估计结果。

同时将样本扩大到N=1 000，2 000，5 000，以此分析在大样本条件下各种参数估计方法的表现。从仿真结果可以看到(1)受限于篇幅，在正文中未报告大样本条件下的详细仿真结果，有兴趣的读者可联系作者索取。，此时OMD方法会较少地受到样本条件的限制，并且在参数估计上也取得了较好的表现。同时，与BUC和DvS方法相比，OMD估计产生的标准偏差确实要小于其他两种方法，由此也印证了Muris提出的观点：使用有序响应变量类别的更多信息，可以获得更有效的估计结果[7]。另一方面，也可以发现，基于BUC、CML和DvS三种方法产生的系数估计值在大样本条件下也没有产生明显的劣势。综合以上在大样本以及小样本条件下的表现，我们建议在估计固定效应的面板有序响应模型时，可以选择使用BUC、CML或者DvS方法。

(三)假设检验的仿真结果比较

由于OMD方法在理论上可以获得更有效的估计结果，也就是说，参数估计量具有更小的渐近方差，那么由此提出的问题是，更小的渐近方差是否会导致在参数的假设检验过程更容易拒绝不显著的原假设，从而形成更准确的检验结论？从更广泛的意义上来看，以上四种估计方法在参数的假设检验阶段是否存在差异？分析这一问题有助于更加全面地综合比较各种参数估计方法的优劣。因此，基于这一目标，本文从假设检验的显著性水平(size)和检验功效(power)两个角度进行分析。

1.检验显著性水平的仿真结果比较

首先，仍然按照上述模型(19)和(20)生成仿真样本数据，并设定待检验参数的真实值为β1=0.5，β2=1.5。然后，建立待检验的原假设H10：β1=0.5，H20：β2=1.5，分别使用上述四种方法估计模型参数，并建立t统计量。设定检验的名义显著性水平为5%，因此从理论上来看，依据t统计量值而拒绝原假设的实际显著性水平应该也等于5%。不同的是，每种参数估计方法最终获得估计值的准确性会不同，并且每种方法计算参数估计量方差的思想也不同。例如，DvS和OMD方法按照最小距离估计思想来计算最后参数估计量的方差，BUC方法按照组群(个体)调整思想来计算稳健的估计量方差，CML方法则直接计算，没有对估计量的方差做出调整，由此导致基于不同方法所获得的假设检验的实际显著性水平也会不同。

表2报告了在小样本条件下，通过100次重复实验所获得的关于参数假设检验的实际显著性水平。不难发现，由于OMD方法在小样本条件下存在较大的参数估计偏误，因此这种方法在假设检验阶段也存在非常明显的水平扭曲现象。例如，当N=100，T=6时，拒绝原假设的实际显著性水平(假设检验犯第一类错误的概率)分别为0.93和0.92，即使当样本从N=100上升到N=500时，假设检验的实际显著性水平仍然有0.34和0.37。同时，也可以发现，虽然CML方法在小样本条件下具有良好的参数估计结果，但是在对模型参数进行假设检验时，这种方法也存在较为明显的水平扭曲现象。在各种样本(N和T)的组合下，由CML方法产生的最小的实际检验显著性水平也达到0.34和0.41，与标准的名义显著性水平5%仍然相差较远。相对而言，BUC和DvS方法都可以获得较好的检验结果，具体如表2中所示。

表2 小样本条件下参数假设检验的显著性水平

同时，也将样本从N=100，200，500放大到N=1 000，2 000，5 000，观察在大样本条件下，BUC、CML、DvS和OMD四种方法假设检验结果的表现。我们看到，当样本增大时，例如，当N=5 000时，由OMD方法获得的拒绝原假设的实际显著性水平也具有良好表现，结果与名义显著性水平值都较为接近，这主要是由于在大样本条件下，OMD方法可以产生有效的估计结果。但是，CML方法在大样本下仍然存在较为严重的显著性水平扭曲现象，结果与5%的名义显著性水平都相差较远，产生这一问题的原因则在于，CML方法在估计模型参数时并未对参数估计量的方差做出调整。另一方面，BUC和DvS方法在大样本条件下的假设检验仍然有较好的表现结果。

2.检验功效的仿真结果比较

考察检验方法优劣的另一标准是分析该方法在检验功效上的表现，因此在仿真模拟中，首先令β1≠0.5(或者是β2≠1.5)，生成样本数据(2)在数据生成中，令β1分别取0，0.1，0.2，0.3，0.35，0.4，0.45，0.55，0.6，0.65，0.7，0.8，0.9等数值，以此观察在这些取值下，关于β1检验功效的变化并绘图得到图1(a)。同理，令β2分别取0.2，0.5，0.7，1，1.1，1.2，1.3，1.4，1.6，1.7，1.8，1.9，2，2.2，2.5，观察在这些取值下，关于β2检验功效的变化并绘图得到图1(b)。；然后建立原假设H10：β1=0.5(H20：β2=1.5)，使用t统计量进行检验。那么，从理论上来看，当设定真实参数β1≠0.5(或β2≠1.5)时，拒绝该原假设H10：β1=0.5(H20：β2=1.5)的概率应该趋向于1。因此，较高的拒绝原假设的概率说明该检验方法(相应地说明与该检验方法相关的参数估计方法)具有较好的表现。图1(a)报告了在小样本(N=200，T=4)条件下，随着参数真实值β1的变化，拒绝原假设H10：β1=0.5的实际概率分布；图1(b)报告了随着真实值β2的变化，拒绝原假设H20：β2=1.5的实际概率分布。考虑到CML方法在前述检验显著性水平的分析中具有较差的表现结果，因此在检验功效的比较中，我们没有包含CML方法。

从图1(a)及1(b)的结果可以看出，当设定的参数真实值在检验值的左侧时，如β1<0.5或β2<1.5，使用OMD方法获得的拒绝原假设的检验功效要高于BUC和DvS方法，但在检验值的右侧，如当β1>0.6或β2>1.9时，BUC和DvS方法获得的检验功效要略高于OMD方法。整体来看，当β1和β2的参数真实值偏离0.5及1.5较远时，使用BUC、DvS和OMD方法都可以获得非常好的检验功效，拒绝原假设的实际概率都趋向于100%。

同时，本文也分析了在大样本(N=2 000，T=4)条件下，随着参数真实值β1和β2的变化，拒绝原假设H10：β1=0.5、H20：β2=1.5的实际检验功效。可以发现，此时BUC、DvS和OMD三种方法具有非常相似的检验功效，并且三种方法对β1和β2值的变化都具有较大的敏感性，只要真实值偏离待检验值(0.5和1.5)的距离在0.1及0.2以上，t统计量的检验功效就可以达到100%。

结合以上在检验显著性水平和检验功效两个方面的比较结果，本文认为，BUC和DvS方法的结果要优于其他两种方法。进一步，将参数估计和假设检验两个阶段的比较结论相结合，本文建议，对于固定效应面板有序响应模型可优先使用BUC和DvS参数估计方法。

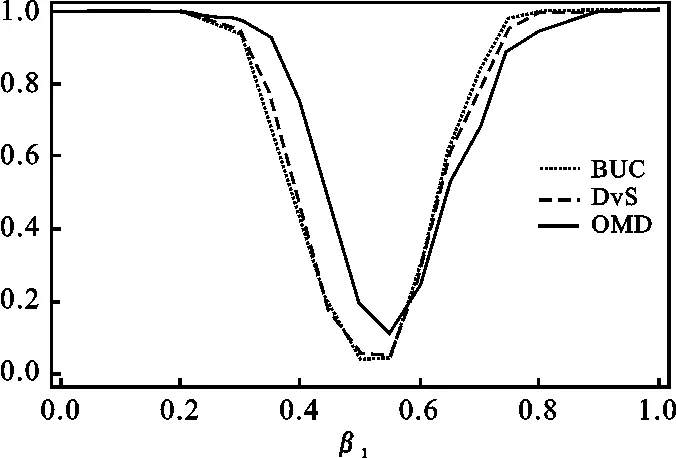
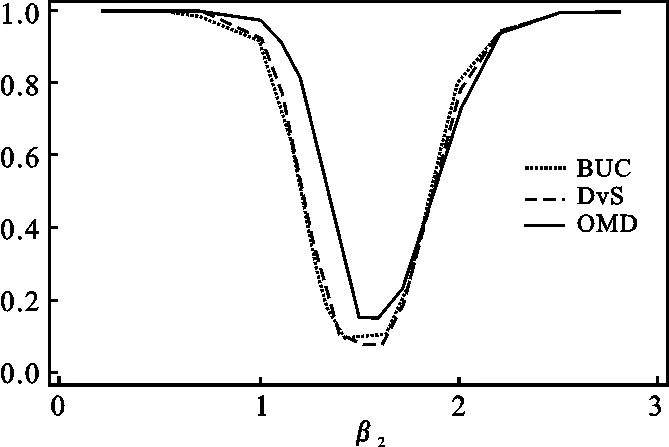
(a) (b)图1 小样本参数β1和β2的检验功效分布

四、结论与建议

本文主要对固定效应面板有序响应模型的多种参数估计方法的效果进行仿真比较，所得结果和结论可以概括为：

第一，从参数估计的仿真比较来看，在小样本条件下，DvS、BUC和CML方法都可以获得较好的参数估计结果，OMD方法会产生较严重的估计偏误，特别是当样本的时间维度(T)较大时，由OMD方法获得的参数估计值会严重偏离真实值。在大样本条件下，以上四种方法都可以获得渐近一致的估计结果，并且OMD方法估计的参数标准差要略低于其他三种方法。产生以上估计结果的原因在于，OMD方法在估计参数时更加充分地利用了有序响应变量的类别信息，对于固定维数(N和T)的面板有序响应模型，如果有序响应变量的类别共有J类，那么OMD方法总共有(J-1)T种不同方式来利用有序变量的类别信息，因此这种方法在大样本条件下的估计结果会更有效。但是，当样本较小时，特别是当(J-1)T在数值上趋向或超过N时，这种方法的估计偏误也会非常大。相反，DvS和BUC方法只是按照(J-1)种方式部分利用了有序响应变量的类别信息，因此在大样本条件下只能获得一致的估计结果，但是在小样本条件下也会更稳健。CML方法虽然也充分利用了有序响应变量的类别信息，但是在估计参数时，该方法并未对方差估计量做出个体调整，因此也只能获得一致的估计结果。另一方面，从四种方法适用的前提假设来看，OMD和CML方法要求基于不同期构成的解释变量的方差矩阵具有正定性，该条件相当于要求解释变量不能包含一些不随时间变化的变量(如性别)，同时也不能包含时间效应变量，这在一定程度上也限制了OMD和CML方法的应用范围，而DvS和BUC方法则没有这种限制。

第二，从假设检验的比较结果来看，由于在小样本条件下OMD方法会产生严重的估计偏误，因此这种方法在假设检验的实际显著性水平上也存在非常显著的小样本扭曲现象。当样本增大时，水平扭曲现象可以得到控制。CML方法由于未对方差估计量做出调整，因此在假设检验过程也存在非常严重的水平扭曲现象。DvS和BUC方法可以产生良好的检验结论，从假设检验的显著性水平和检验功效两个方面看，在大样本和小样本条件下，这两种方法都可以获得较稳健的检验结论。

结合以上参数估计和假设检验的比较结果，我们建议，对于固定效应的面板有序响应模型，优先使用DvS或者是BUC方法进行参数估计，并基于估计结果开展假设检验工作。