MATLAB在线性代数实验教学中的应用研究

杜红林

摘要：借助MATLAB数值计算应用软件，提高高等学校工科专业的学生学习线性代数课程的学习兴趣。本文以解决矩阵特征值的教学为实例，阐述了通过MATLAB辅助线性代数实验教学的应用价值。

关键词：MATLAB;特征值;特征向量;几何意义

中图分类号：TP3      文献标识码：A

文章编号：1009-3044（2019）20-0114-02

开放科学（资源服务）标识码（OSID）：

线性代数是大学理工科学生所必备的基础知识和重要的数学工具，它一方面是学生学习后继专业课程的基础，另一方面，由于线性代数的高度抽象性，它又是让学生望而生畏的枯燥课程。因此，作为教师，如何改进新的教学手段，引进新的教学方法，采取更加合理的教学模式，帮助学生更好地理解线性代数课程的理论知识，并让学生能够灵活应用到实践中去，这是深化高等学校工科专业线性代数课程实验部分教学改革的主要途径之一，同时也是该课程任课教师在教学过程中值得思考和研讨的问题[1-4]。

以往的线性代数教学偏重的完备课程理论体系学习，过于注重的基本概念的掌握，忽视相应的与实践相结合，采取严格的数学逻辑思维训练和计算量大的教学模式，会使得学生学习起这门课程内容感觉枯燥、抽象，导致失去主动学习的兴趣和热情。进入21世纪，随着多媒体辅助教学技术的发展，借助MATLAB数学软件，将实验教学融入线性代数的课堂教学，不仅可以让学生摆脱繁重乏味的思考、不必要而又复杂的数学演算，而且可以加强学生对书本中抽象概念的理解和掌握。下面结合线性代数中的实验教学，本文将谈谈借助MATLAB软件改进线性代数教学的一点体会予以分享。

1 MATLAB的优越性

上世纪70年代中期，美国新墨西哥大学的计算机系的系主任Cleve Moler教授在给学生讲授线性代数时，发现学生在繁琐的计算上花了太多时间，为此，他为学生编写了一个接口程序，取名为MATLAB，即Matrix Laboratory的缩写，意思为“矩阵实验室”， 这就是 MATLAB这个应用软件产生的背景。1984年，工程师John Little觉察到MATLAB的应用前景不应该仅是单纯的数学领域，更应该是广阔的工程领域。于是，他与Cleve Moler成立了MathWorks公司。由于MATLAB强大的数值计算功能，很快使其在众多软件中脱颖而出。目前，在国内外各大高校中，MATLAB已成为理工科专业基础课程必备的基本教学工具。

在线性代数教学过程中，可以充分利用MATLAB软件强大的计算功能、程序设计语言简单、绘图功能方便等特点将抽象的概念变得直观，将复杂的数学计算变得简洁，加深学生对概念的理解，增强学生对线性代数的学习兴趣，培养学生获取知识的主动性。

2 借助MATLAB数值计算应用软件进行实验教学

在线性代数的教学过程中，大量复杂而又繁琐的计算分散了学生理解问题本身的精力，造成了学生们忙于应付计算，轻视了方法原理的学习，而利用MATLAB软件进行实验教学，可以较好地解决这一问题。

接下来就以线性代数中的一个重要内容为例说明MATLAB的作用。

实验内容：特征值、特征向量的概念和意义[5]。

线性代数中许多抽象概念的讲解，往往过于强调抽象思维能力而忽视了空间想象能力。例如，对于矩阵的特征值与特征向量的学习，学生往往只知其一：只知道如何套用公式求矩阵特征值和特征向量;不知其二：不知道特征值和特征向量究竟表示什么，有什么几何意义。在教学过程中，可以借助MATLAB软件，通过如下的方式帮助学生理解这一抽象的概念。

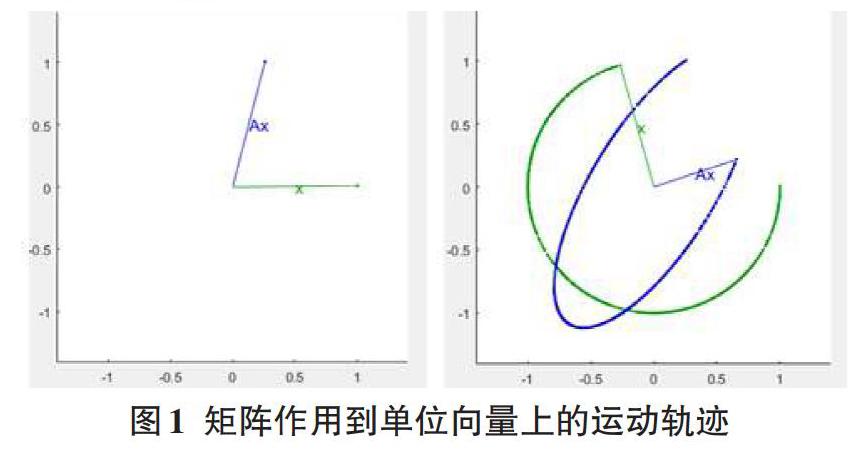
在MATLAB命令窗口输入eigshow命令[6]，可以打开一个特征值、特征向量的演示窗口，其中系统默认的矩阵[A=1434112]，绿色线段表示单位向量[x=（1， 0）T]，蓝色线段表示向量[Ax]。当鼠标在单位圆上移动[x]，矩阵[A]作用到向量[x]后的结果[Ax]也随之变化。

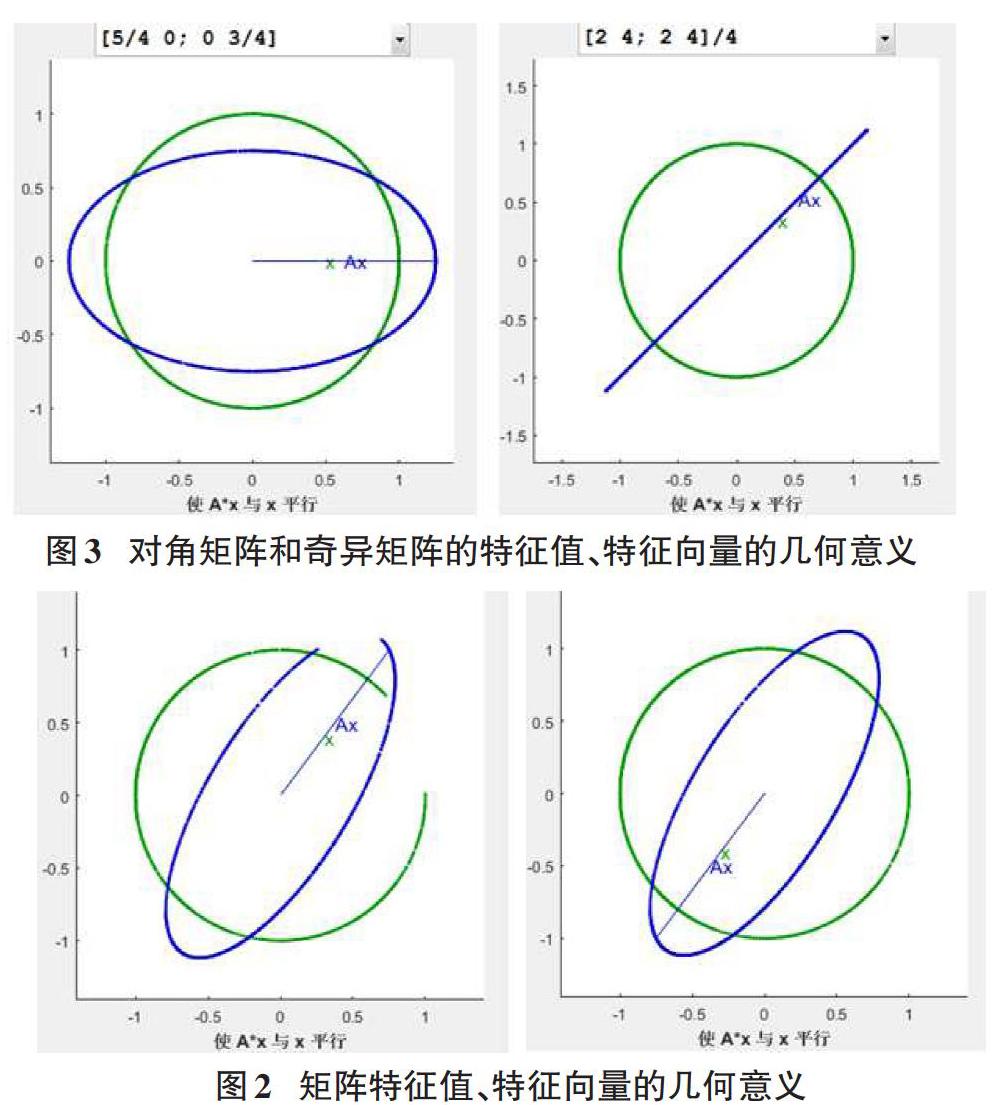
图1显示了向量[x]在矩阵[A]的作用下的变化过程，可以看出向量[Ax]的轨迹是一个椭圆。那么，什么是特征值、特征向量呢？从数学的定义看，满足[Ax=λx]的非零向量[x]称为特征向量，[λ]称为特征值。这是一个抽象的数学概念，但通过给学生演示[x]和[Ax]的运动轨迹，可以直观地观察到：所谓特征向量，指的是与[Ax]平行的向量[x]，此时矩阵[A]的作用仅仅是把单位向量[x]拉伸[λ]倍，[λ]即为特征值。图2显示了矩阵[A]的特征值和特征向量。第一个特征值是正数，所以[Ax]位于特征向量[x]的顶部，[Ax]的长度即为特征值，在这个例子中为[54]。第2个特征值是负数，所以[Ax]平行于特征向量[x]，但方向相反，[Ax]的长度为[12]，所以相应的特征值为 [-1/2]。

细心的学生会发现，图2中的两个特征向量很接近但并不完全落在椭圆的长、短轴上。那么，可以引导学生思考：对于什么样的矩阵，特征向量恰好落在椭圆的长、短半轴上？如果矩阵奇异，那么椭圆又会发生什么样的变化？通过上述的引导和讨论，我们选择对角矩阵[A=540034]和奇异矩阵[A=1212]，然后观察[x]和[Ax]的运动轨迹，见图3。

通过直观演示，结合简单运算，可以发现，对角矩阵的特征向量刚好落在椭圆的长半轴和短半轴上，（实际上，如果矩阵[A]对称，那么其特征向量一定落在椭圆的长、短轴上），而单位向量[x]在奇异矩阵作用下的轨迹退化成了一条线段。

3 结语

在线性代数课堂上引入实验教学，将抽象的高等数学的学习与Matlab这款应用软件相结合，无疑是一种行之有效的计算机辅助线性代数教学的学习途径，有利于提高学生学习线性代数的兴趣，提升教学效果，促进现代教学改革。同时不仅消除了学生对高等数学学习的枯燥和抽象，还能提高学生运用数学知识解决实际问题能力。

參考文献：

[1] 徐利治.关于线性数学教育与数学改革的看法及建议[J].数学教育学报，2000，9（2）：1-2.

[2] 王海侠，孙和军，王青云.改进线性代数教学方法的几点想法[J].高等数学研究，2010，13（6）：13-15.

[3] 周琳.将数学实验融入线性代数课的研究与实践[J].辽宁科技学院学报，2008，10（2）：63-64.

[4] 金波.数学实验在《线性代数》教学中的应用探索[J].科技信息，2013（7）：319-319.

[5] 同济大学数学系.工程数学，线性代数.第6版[M].高等教育出版社，2014.

[6] Moler C B.Numerical Computing with MATLAB：Revised Reprint[M].SIAM，2008.

【通联编辑：张薇】