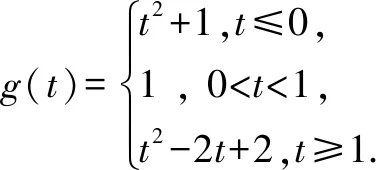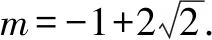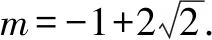例析求二次函数最值的“四步曲”

2019-09-19朱继娟

数理化解题研究 2019年25期

朱继娟

(四川省南充市嘉陵第一中学 637000)

一、二次函数求最值问题

对于二次函数求最值问题，有人把它归纳为四类：轴定区间定、轴定区间动、轴动区间定、轴动区间动.也有人把它归纳为两类：含参数的二次函数求最值问题和不含参数的二次函数求最值问题.其实，这两种分类方法思想都可以将解决最值问题时的基本步骤归纳为八个字，即“一看、二求、三判、四得.”具体来说求二次函数最值的“四步曲”是：第一步看二次函数的开口方向，第二步求二次函数的对称轴，第三步判断二次函数在给定区间上的单调性，第四步得出结果.下面通过具体实例对上述“四步曲”进行说明.

二、例题解析

例1 求函数f(x)=x2-4x在[-1,1]上的最大值和最小值.

故归纳解题步骤如下：

此类题目我们可以做如下总结：

当给出的区间不为具体数字时，怎么处理相对简洁呢，来看一看下面的例题：

例2若函数f(x)=x2-2x+2，x∈[t,t+1],t∈R上的最小值为g(t)，试写出g(t)的函数表达式.

当对称轴在区间左边(含端点)即1≤t时，函数f(x)在区间[t,t+1]上为增函数；

当对称轴在区间右边(含端点)即1≥t+1时，函数f(x)在区间[t,t+1]上为减函数；

当对称轴在区间内(不含端点)即t<1

第四步得出结果：

当t≥1时，fmin(x)=f(t)=t2-2t+2；

当t≤0时，fmin(x)=f(t+1)=t2+1；

当0

故归纳解题步骤如下：

当t≥1时，函数f(x)在区间[t,t+1]上为增函数，fmin(x)=f(t)=t2-2t+2；

当1≥t+1即t≤0时，函数f(x)在区间[t,t+1]上为减函数，fmin(x)=f(t+1)=t2+1；

当t<1

我们可以得出这样的结论：

对于二次函数求最值,轴定区间动这一类题，对称轴与区间的位置关系有三种：(1)对称轴在区间左边(含端点)；(2)对称轴在区间右边(含端点)；(3)对称轴在区间内(不含端点)，先确定参数范围，然后再判断函数在给定区间上的单调性，最后再求结果.

当有参数出现时，有人觉得这样的问题难度陡增.其实也有规律可寻：

例3已知函数f(x)=x2-2ax+2，x∈[-1,1]，求函数f(x)的最小值.

分析第一步看二次函数的开口方向：开口向上；第二步求二次函数的对称轴：x=a；第三步判断函数在给定区间[-1,1]上的单调性：这时不难发现此题中对称轴不确定，但区间确定，此时对称轴与区间的位置关系有三种：(1)对称轴在区间左边(含端点)；(2)对称轴在区间右边(含端点)；(3)对称轴在区间内(不含端点).

当对称轴在区间左边(含端点)即a≤-1时，函数f(x)在区间[-1,1]上为增函数；当对称轴在区间右边(含端点)即a≥1时，函数f(x)在区间[-1,1]上为减函数；当对称轴在区间内(不含端点)即-1

第四步得出结果：

当a≤-1时，fmin(x)=f(-1)=3+2a；

当a≥1时，fmin(x)=f(1)=3-2a；

当-1

故归纳解题步骤如下：

解函数f(x)=x2-2ax+2开口向上，对称轴为x=a.当a≤-1时，函数f(x)在区间[-1,1]上为增函数，fmin(x)=f(-1)=3+2a；当-1

然后，我们对此做一总结归纳即可：

对于二次函数求最值轴动区间定这一类题时，f(x)=ax2+bx+c(a>0)在区间[m,n]上的最值分为以下三种情况：

当然，如果区间和对称轴都不确定时，我们也可以根据这样的步骤将其分析完整：

分析第一步看二次函数的开口方向：开口向上；第二步求二次函数的对称轴：x=2m+1；第三步判断函数在给定区间[m,m+2]上的单调性：这时不难发现此题中对称轴不确定，且区间不确定，但对称轴与区间的位置关系也只有三种：(1)对称轴在区间左边(含端点)；(2)对称轴在区间右边(含端点)；(3)对称轴在区间内(不含端点).

当对称轴在区间左边(含端点)即2m+1≤m时，得m≤-1，此时函数g(x)在区间[m,m+2]上为增函数；

当对称轴在区间右边(含端点)即2m+1≥m+2}时，得m≥1，此时函数g(x)在区间[m,m+2]上为减函数；

当对称轴在区间内(不含端点)即m<2m+1

第四步得出结果：