基于GA-GRU环境空气污染物预测研究

(西南科技大学 信息工程学院，四川 绵阳 621000)

大气污染形势严峻，以可吸入颗粒物(PM10)、细颗粒物(PM2.5)为特征污染物的区域性大气环境问题日益突出，严重危害着人们的身心健康和生活环境质量。随着我国工业化、城镇化的快速推进，资源消耗持续增加，空气污染防治压力持续加大。了解空气质量现状，及时采取有效措施进行治理，是改善空气质量的唯一途径[1]。因此，对环境空气污染物浓度进行预测成为近几年的研究热点。

环境空气污染物浓度预测分为两类：机理模型和统计学习模型[1]。其中，机理模型是根据气象、地理环境和污染源模拟污染物累积、释放或扩散过程[2]，虽具有很强的适应性、模型参数易调整等优点，但过于依赖精确的数学模型，实现复杂且需要高计算能力的计算机和较长的运行时间[3-4]；统计学习模型不仅善于描述复杂的非线性关系，还避免了对精确数学模型的过分依赖，具有较好的预测精度和运行效率[5-6]。

支持向量机(Support Vector Machine,SVM)、非线性回归、人工神经网络(Artificial Neural Network,ANN)和深度信念网(Deep Belief Networks,DBNs)等统计学模型已成功地应用于环境空气污染物浓度预测研究[7-9]。文献[7]运用ANN模型预测PM2.5小时浓度，预测系统结构简单且具有较好地预测能力，但存在局部最优和过拟合问题；文献[8]在文献[7]的基础上利用小波分解和SVM对PM10浓度时序数据进行预测，克服了ANN导致的局部最优和过拟化问题，并且提升了泛化能力，但是数据单一，未做缺失值处理影响预测精度又缺乏数据深度相关性的分析。郑毅[9]等人基于DBNs方法较好的预测出区域整体的PM2.5日均值变化趋势，并与RBF的人工神经网络方法进行比较，得出DBNs方法具有更好的预测精度，但存在局部优化、收敛速率慢和由于采用滑动窗口而导致更早时间之前的序列数据信息丢失问题。文献[10]运用主成分分析(Principal Component Analysis,PCA)对气象因子和空气污染物因子进行降维和提取，并结合最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)，建立环境污染物PM2.5浓度预测模型，克服了文献[7]存在的维度灾难问题，但局部优化能力和泛化能力弱。上述方法虽都取得较好的预测结果，但仍存在以下几个问题：① 缺失值未做处理，使时序信息提取不完整；② 维度灾难，输入因子增多，伴随着训练样本大幅度增多，在实际应用中难以满足；③ 不相关因子的干扰，加入非标识的特征因子，不仅降低模型性能而且干扰模型学习；④ 时间序列内在依赖关系未进行关联，导致时间序列信息的丢失。基于以上问题和文献[10]多指标降维思想的启发，作者考虑到门控循环单元(Gates Recurrent Units,GRU) 神经网络是在传统循环神经网络(recurrent neural network,RNN)上进行改进的，它既能继承RNN探索序列数据内在依赖关系的能力，又能解决传统RNN因序列过长而导致的梯度消失、训练时间长和过拟合等问题，并提升局部优化能力和网络泛化能力[11]。

因此，本文将绵阳市4个监测站点的环境空气污染物浓度数据和气象数据作为数据集，提出将遗传算法(Genetic Algorithm,GA)[12]和门控循环单元神经网络相结合的环境空气污染物PM2.5小时浓度预测模型，以提高空气污染物浓度预测模型的训练时间、预测精度和网络泛化能力等，并通过TensorFlow-GPU深度学习平台分别与GRU、DBNs两种预测模型的预测效果进行对比分析，验证所设计的GA-GRU预测模型的有效性、合理性。

1 研究区域

绵阳，隶属于四川省，中国唯一的科技城，是重要的国防科研和电子工业生产基地，此外，矿产资源丰富，煤、石油、轻纺工业等发展迅速，因此，PM2.5是绵阳地区中主要的大气污染物之一[13]。

绵阳市环境空气污染物的监测采用24 h自动监测的形式，全市共设有4个国控环境空气污染物监测站点。本实验数据采用绵阳市2015年1月至2017年12月逐小时环境空气污染物数据(PM2.5、PM10、SO2、NO2、CO、O3)和每小时更新一次的气象数据(温度、温差、压强、气压、湿度、风速、风向、露点温度、可见度、降水量)，总数据集共10万余条。

2 数据预处理

2.1 缺失值算法

在实际数据集中，随机缺失数据占有相当的比例，数据值缺失是数据分析中经常遇到的问题之一。对缺失值进行填充，能保证信息完整性和结论的准确性。因此，采用线性分段插值与日均值加权和算法进行缺失值填充。

① 缺失标签。对于一个有缺失值的时间序列xt，其表示第T个时间步对应的时刻(x1=0)，如式(1)所示。

(1)

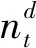
(2)

在原有神经网络结构的基础上，结合均值填充和线性插值，设计出本文加权和缺失值处理算法，如式(3)所示。

(3)

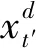
2.2 风力编码

实际监测到的气象数据，风力大小属于分类值且具有离散特性，不具备特征之间数据的相关性。因此，在这些数据进入预测模型前，需对数据进行风力编码处理，即采用One-Hot编码，通过One-Hot编码，扩充输入特征，提高建模的可能性，见表1。

表1 风力编码表

其中，小于或等于1级风用“0”表示，“1”表示大于一级风。

2.3 数据归一化处理

为加快预测模型收敛速度，在采用加权和算法对研究数据进行缺失值处理后，结合归一化算式(4)将研究数据进行归一化处理。

(4)

在模型预测得到[0,1]之间一个数值后，应用式(5)进行去归一化，进行模型性能分析评价。

(5)

3 遗传算法-门控循环单元网络模型

3.1 GA-GRU预测模型

为减少相关因子的干扰，选择用GA算法从10个气象因子和5个主要的空气污染物浓度中筛选出GRU循环神经网络模型的输入因子，实现对GRU循环神经网络输入特征的优化与选取，即基于GA-GRU模型的PM2.5浓度预测，其中，GA-GRU预测模型如图1所示。

图1 GA-GRU算法框架

(6)

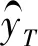
3.2 GA筛选输入因子

遗传算法是一种高效全局搜索可并行化的优化方法，适合大规模问题以及多维多模态问题的求解[14]。面对优化复杂性问题，GA算法可避免精确建模和繁琐运算，只需运用GA算法的选择、交叉和变异三种算子便可确定最优解。

首先，定义群体规模每个因子的编码形式，每个元素分别对应一个因子，取值为“0”或“1”。取“0”为不参与GRU神经网络的训练；同理，取“1”即参与。具体步骤如下。

① 在1个临时群体中，复制n个原群体中的个体。

② 在0～1之间产生一个随机数，若该随机数大于预先设定的交叉概率，则随机选择2个原群体中的个体，并在随机确定的若干位置上进行元素交换，并将交换后的向量放入临时群体中。

③ 若随机数不大于交叉概率，则随机选择原群体中的一个个体，并对其中每个位置随机产生1个随机数。反之，对该位置进行变异操作后，将其放入临时群体中。

④ 重复步骤②和步骤③，直到群体中有n个个体。

⑤ 选出适应度最高的n个临时群体的个体，组成新一代群体进行遗传。

⑥ 算法迭代循环，直至满足设置的目标，遗传操作结束。

⑦ 选取适应度值最高的l维个体，其中值为1的元素对应的影响因子即为输入因子集。

下面分别给出选择算子、交叉算子和变异算子的算法。

① 选择算子。个体i的选择概率Ps如下：

(7)

式中，num为群体规模；E(w)为适应度优化目标函数，评价个体优劣，其计算公式为

(8)

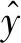
② 交叉算子。采用实数编码种群个体，对配对的粒子i、j进行交叉运算，过程如下。

位置交叉：

(9)

速度交叉：

(10)

式中，α1，α2为交叉概率Pe，取值[0,1]。

③ 变异算子。对第i个个体进行变异运算。

位置变异：

(11)

速度变异：

(12)

(13)

式中，Xmin、Xmax为粒子位置上下界；Vmin、Vmax为变异速度的最小和最大值；g为当前时刻迭代次数；Gmax为最大进化次数；r1、r2、r3为各自的变异概率Pm，取值范围[0,1]。

3.3 门控循环单元(GRU)

门控循环单元神经网络是在传统循环神经网络上进行改进的，它不仅继承了传统循环神经网络探索序列数据内在依赖关系的能力，又解决了因序列过长而导致的梯度消失、训练时间长和过拟合等问题[11]。门控循环单元网络模型如图2所示。

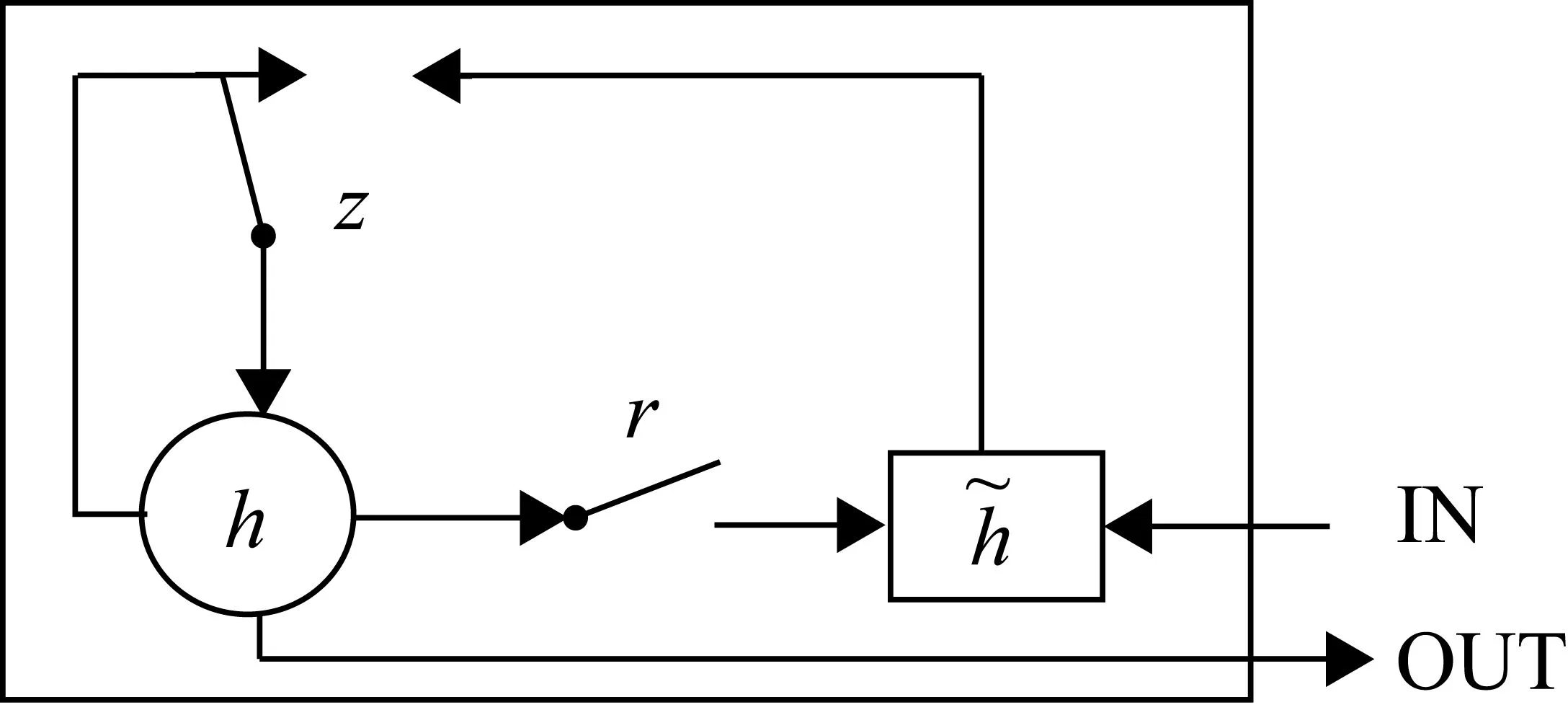
图2 GRU单元模型

图2中，⊙为Hadamard乘积；z为重置门；r为更新门。其中，更新门和重置门计算关系式为

zt=g(xtUz+ht-1Wz)

(14)

rt=g(xtUr+ht-1Wr)

(15)

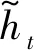
(16)

式中，ht为当前时刻的输出和传递到下一时刻的信息，该过程需要更新门的激活结果zt，计算式为

(17)

其中，zt×ht-1的Hadamard乘积是当前时间步最终输出结果，也是下一时间步输入和参与下一时间步的运算。

4 仿真实验

为了验证所设计的GA-GRU环境空气污染物时序预测模型，将绵阳市4个监测站点的气象数据和环境空气污染物数据集分为90%的训练集、5%的测试集和5%的验证集，通过TensorFlow-GPU深度学习平台对所设计的GA-GRU模型进行无监督训练和PM2.5的仿真预测。最后，将GA-GRU预测模型的预测效果分别与GRU、DBNs模型进行对比分析。

4.1 算法性能评价指标

评价模型预测性能优劣，以均方根误差(Root Mean Squared Error,RMSE)、平均绝对误差(Mean Absolute Error，MAE)和一致性指数(Index of Agreement,IA)作为评价指标。计算公式如下。

(18)

(19)

(20)

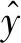
4.2 参数确定

由于存在输入特征维度灾难问题，导致GRU算法计算性能差以及收敛速率过慢。因此，在GRU算法的基础上，引入GA算法。利用GA算法解决维度灾难问题，确定出最优个体。

GA参数：群体规模为num=200，交叉概率Pe=1.0，变异概率Pm=0.050，进化代数为10。根据确定参数，给出GA算法在4个数据集上的最优个体适应度变化曲线，如图3所示。

由适应度优化目标函数(8)可知，较小适应度值表明神经网络系统误差小。因此，结合图3可知，经过10代进化，4个站点的适应度值已达到最小，确定出输入向量的最优个体，即2.2节中第7步值为1的元素所组成的输入向量。

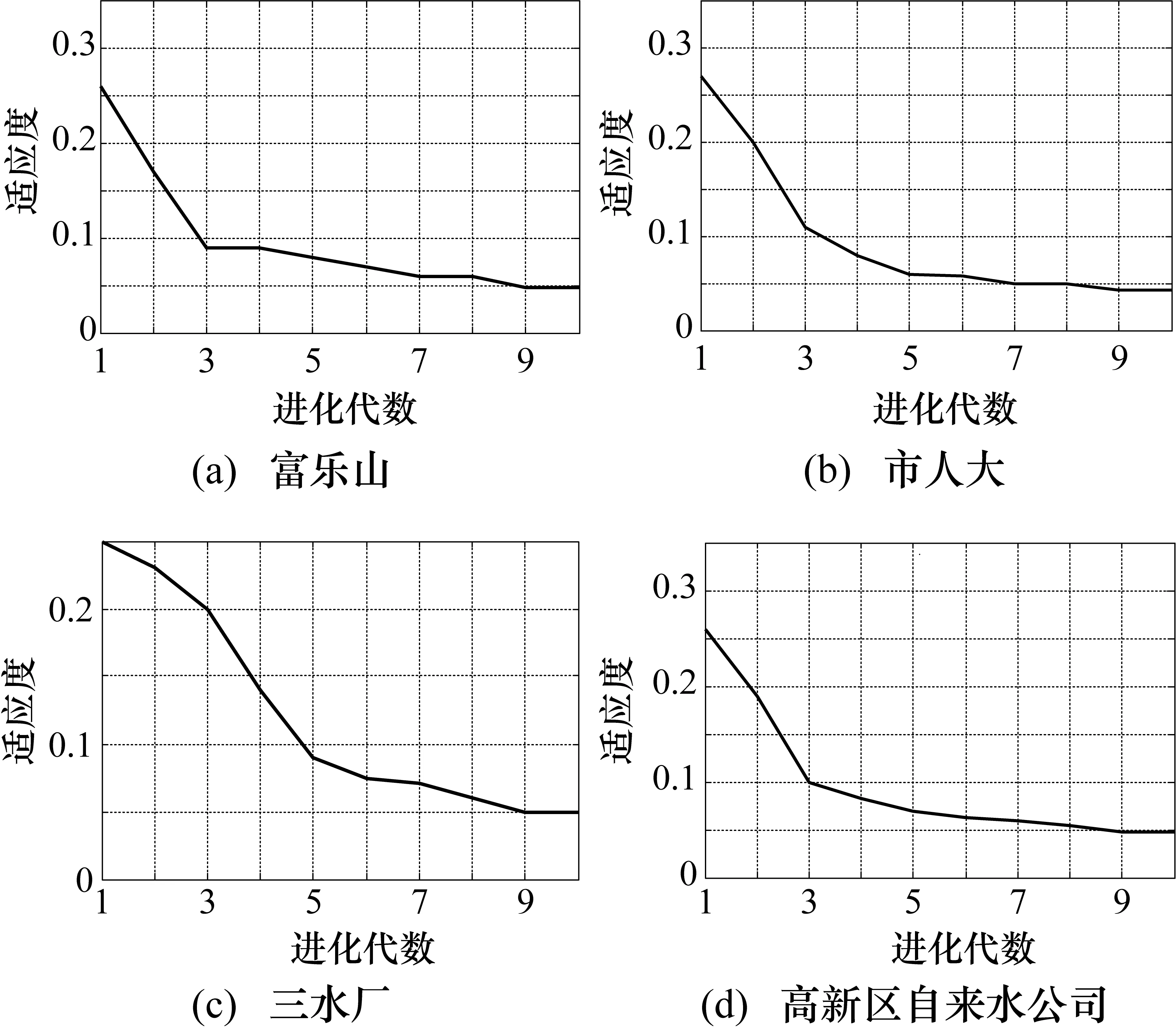
图3 4个站点最优个体适应度值变化曲线

为解决时序信息丢失问题，采用改进后的循环神经网络，即门控循环单元神经网络。通过在4个站点数据集上分别执行网格搜索算法，确定GA-GRU模型的最优深层架构、最优批尺寸(batch_size)、训练步(epochs)、权值初始化函数(init_mode)以及dropout正则化参数。其中，GA-GRU模型中GRU层数的确定，如图4所示。

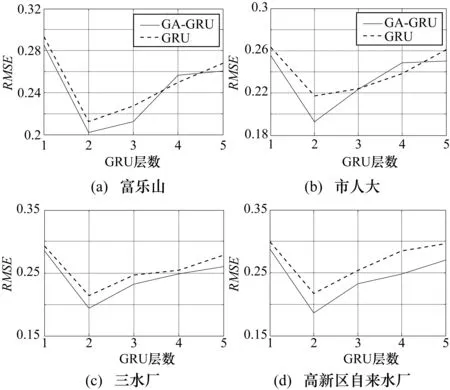
图4 GRU层数变化曲线

图4中，纵轴表示模型性能评价指标。由于模型性能评价指标值越低，模型的性能越好。因此，从图4中可知：当GRU层数为2层时，GA-GRU模型性能最佳。表2给出4个站点的GA-GRU和GRU最优深层架构。

其中，最优深度架构隐藏层包含2层GRU层和1层全连接层，因此，隐藏层并不是越多越好。最后确定的模型参数，如表3所示。

表2 隐藏层层数及神经元数目

表3 模型参数

通过表3确定的最优模型参数，最终分别得到GA-GRU、GRU网络模型在4个监测站点数据集上的训练损失与验证损失图，如图5所示。

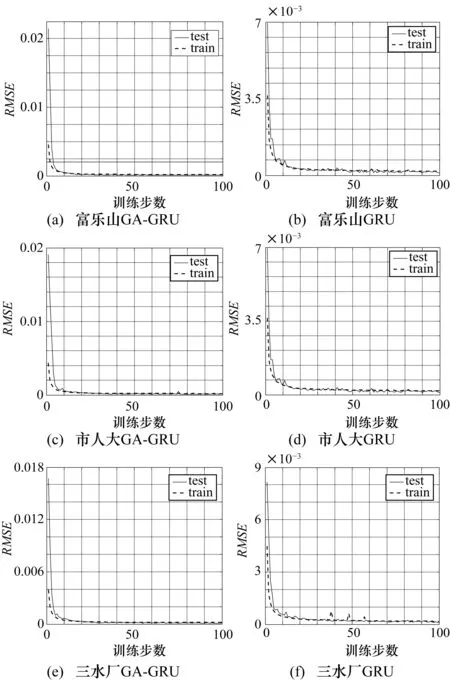
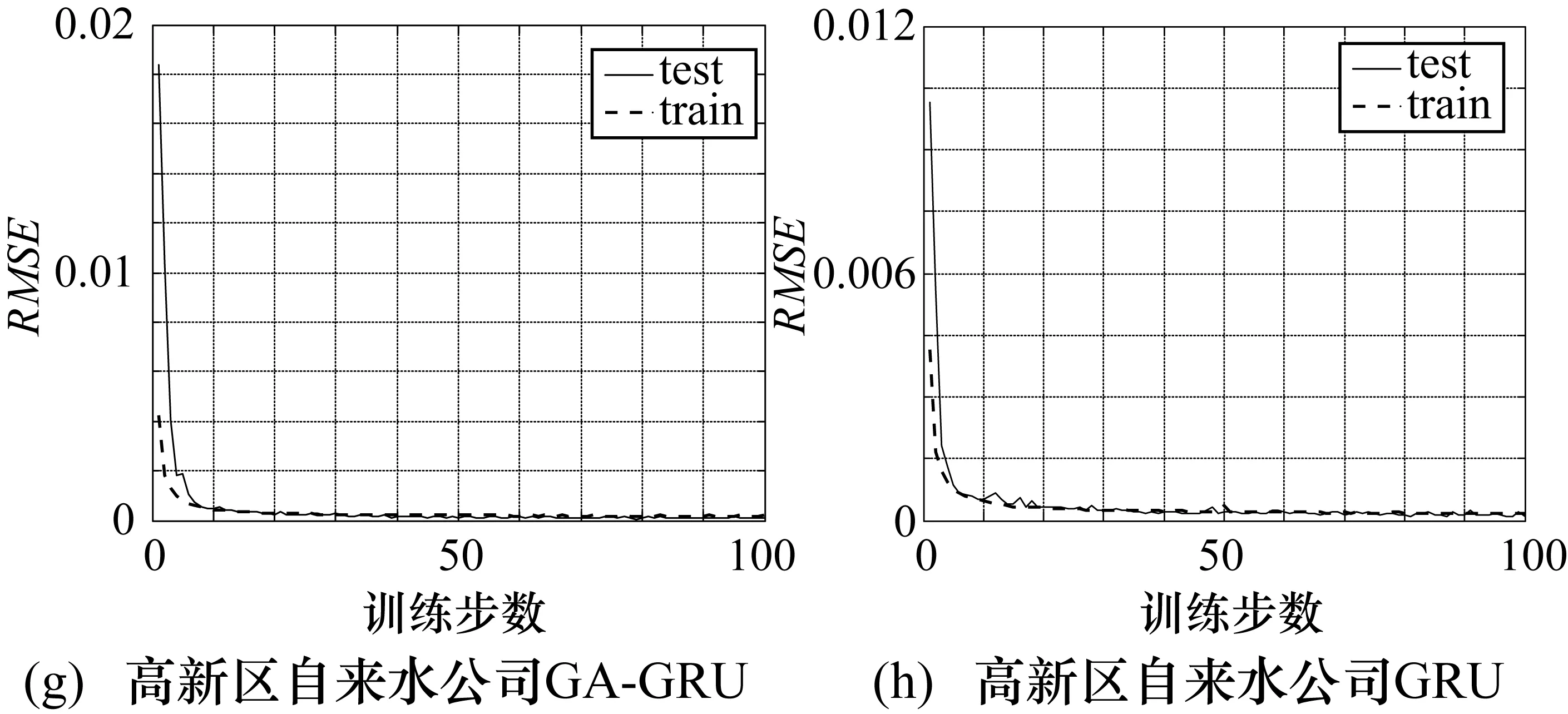
图5 GA-GRU和GRU模型训练损失与验证损失图

其中，“train”、“test”分别表示训练集和验证集上的损失函数；纵轴表示评估预测性能值。结合表3、图5可知，在4个数据集上都有，当批尺寸为20、训练步为100、网络权值初始化参数为glorot_nomal[15]时，GA-GRU模型的处理速度在20个时间步前就开始朝着梯度最小的下降方向收敛，处理速度加快、下降方向准确以及训练震荡更小，并且没有出现过拟合现象。而GRU模型虽然没有出现过拟合现象，但它从第20个时间步后开始收敛，处理速度稍慢、下降方向存在偏差，并且伴有轻微振荡。

4.3 仿真结果

为了验证由4.2节确定的参数，而设计的GA-GRU模型预测精度与性能情况，在绵阳市城区的4个监测站点测试集上，将所设计的GA-GRU模型与GRU模型、DBNs模型进行PM2.5小时浓度预测比较，其仿真图如图6所示。

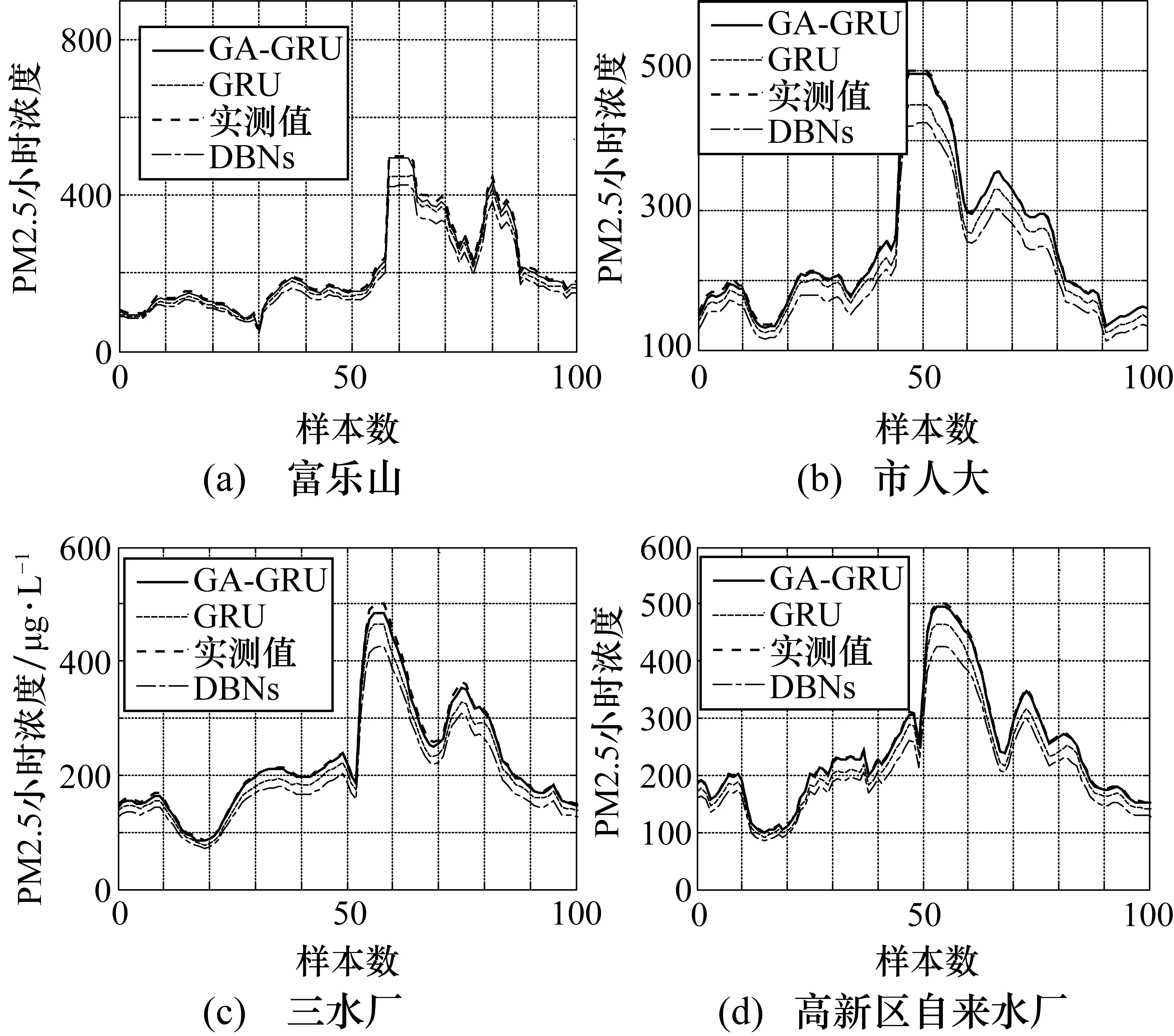
图6 GA-GRU模型在4个站点预测结果比较

图6预测结果表明：与GRU模型、DBNs模型相比，所设计的GA-GRU模型具有高拟合程度和高预测精度，已达到项目所要求的95%。而GRU精度为92%，深度信念网络的精度为88%左右。在富乐山数据集上，当PM2.5小时浓度值达到最大值500 μg/L时，GA-GRU模型预测值达到495 μg/L，而GRU、DBNs分别为450 μg/L和420 μg/L；在市人大数据集上，当PM2.5小时浓度值达到最大值500 μg/L时，GA-GRU模型预测值达到493 μg/L，而GRU、DBNs分别为453 μg/L和425 μg/L；在三水厂数据集上，当PM2.5小时浓度值达到最大值500 μg/L时，GA-GRU模型预测值达到495 μg/L，而GRU、DBNs分别为448 μg/L和425 μg/L；在高新区自来水公司数据集上，当PM2.5小时浓度值达到最大值500 μg/L时，GA-GRU模型预测值达到491 μg/L，而GRU、DBNs分别为447 μg/L和423 μg/L。综上所述，当PM2.5值较大时相较于GRU、DBNs模型，GA-GRU模型能更好获得满意的预测结果。

最后，为了更加全面评价所设计的GA-GRU模型性能,下面列出评价模型性能的3个统计值MAE、RMSE、IA及模型训练时间，如表4所示。

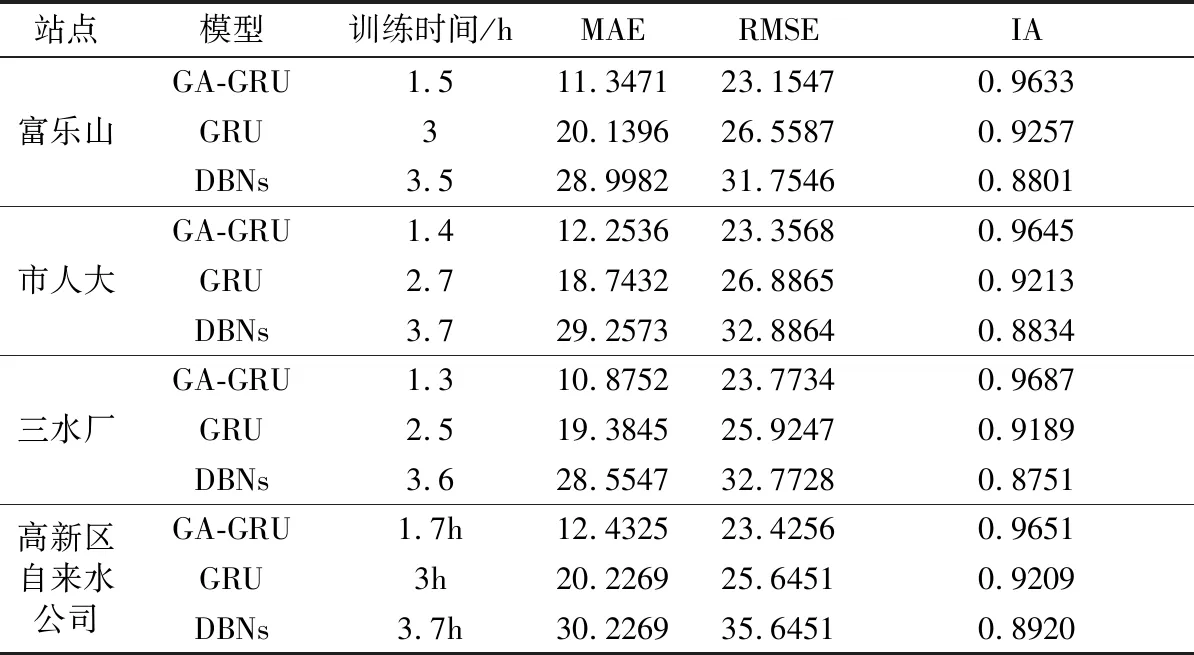
表4 模型预测性能比较结果

从表4可知，与GRU模型、DBNs模型相比，所设计的GA-GRU模型在均方根误差、平均绝对误差和一致性指数这3种性能评价指标中有较好改进。其中，一致性指数(IA)提升尤为明显，表示GA-GRU模型具有更准确的时序预测能力；而平均绝对误差(MAE)、均方根误差(RMSE)较小，表明GA-GRU模型预测精度较高，泛化能力较好，能更加有效地预测PM2.5浓度变化趋势，对空气污染物控制具有有效的指导作用。值得注意的是，从表4训练时间一列可得，GA-GRU训练时间相较于GRU、DBNs模型分别提升了50%、57%左右。因此，GA-GRU模型训练时间上有较大的提升，表明前期GA处理输入特征取得良好的效果。综上所述，所提出的GA-GRU预测模型能有效预测PM2.5小时浓度，并且具有较强的鲁棒性。

5 结束语

所设计的GA-GRU预测模型在环境空气污染物PM2.5小时浓度预测中，对大样本数据集，该模型不仅保留了处理数据维度和输入特征的能力，并且在一定程度上充分挖掘了环境空气污染物因子自身之间与气象因子之间潜在的特征关系。仿真实验结果表明，相较于门控循环单元神经网络模型和深度信念网络模型，GA-GRU预测模型在训练时间、拟合度、泛化能力和预测精度上都有所提升且具有更强的鲁棒性。在未来研究中，将考虑加入影响环境空气质量的其他因素，例如，季节因素、地域因素和车流量等，为相关部门进行空气环境污染防治提供理论支撑与决策依据。