电动车驾驶机器人控制器参数自学习方法研究

(1.东南大学 仪器科学与工程学院，江苏 南京 210096;2.中国人民解放军驻荆州南湖机械总厂军事代表室，湖北 荆州 434007)

随着新能源汽车产业的迅猛发展，电动汽车已成为汽车行业未来的主要发展方向之一。在国内外电动汽车市场大力发展的过程中，用户对电动车的性能要求日渐提升，因此合理有效的电动车测试方法也越来越受到各大电动汽车厂家的重视。其中，转毂试验是电动车整车试验的重要组成部分，新款电动车在投放市场前，需在转毂上进行经济性、动力性、续驶里程等多项测试。

传统的电动车转毂试验需要由经验丰富的驾驶员来完成，这为电动车转毂试验增加了大量的培训和人工成本，同时，试验重复性也难以得到保证。

然而现有的机械式驾驶机器人为了保证其在电动车和传统燃油汽车上的通用性，均具有较为复杂的机械结构，这使得机器人在每次试验前均需进行长时间的安装、示教与车辆驾驶性能自学习。针对机械式驾驶机器人的控制问题，以往大多采用模糊控制和神经控制方法。但模糊系统的模糊控制规则非常难以获取，模糊规则的获取来源比较困难，并且缺乏有效的学习机制；神经网络对语言信息的处理比较欠缺，不能很好地利用专家经验知识[1-2]。

为了解决上述问题，本文首先利用电动车在结构和控制方法上的独特性，依托自行设计的电动车转毂驾驶机器人，采用电信号代替机械结构，避免了烦琐的安装与示教过程，完成对于车辆的精准控制。其次，基于电动车纵向动力学模型，利用参数在线辨识方法，大幅缩短了机器人的在线学习时间。最后，通过控制器参数自整定和在线优化，实现对任意工况曲线的速度跟随，提高了转毂试验效率，消除了人为因素对试验结果的不利影响，对电动车辆的研发和测试都有重要的实际意义。

1 电动车驾驶机器人结构设计

所设计的电动车转毂驾驶机器人由人机交互界面和驾驶机器人控制系统两个部分组成，驾驶机器人的系统结构如图1所示。

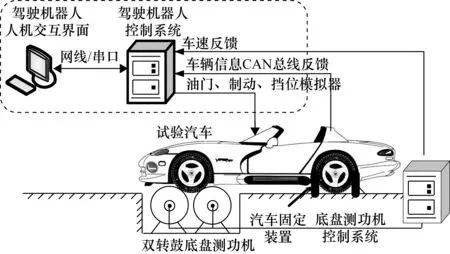
图1 驾驶机器人的系统结构

驾驶机器人的人机交互界面采用网线与驾驶机器人控制系统进行实时通信，实现车辆参数导入和用户自定义工况编辑；完成电动车驾驶风格的选择以及驾驶机器人控制系统反馈的相关车辆信息的保存和下载；在线显示车辆输出速度对设定工况的跟随效果。

驾驶机器人控制系统分别通过网线、CAN总线与人机交互界面、电动车控制器进行数据交互，实现闭环控制。驾驶机器人控制系统利用加速踏板、制动和挡位模拟器分别实现对电动车加速踏板、制动和挡位的协调控制，实现车辆输出速度对用户自定义工况的准确跟随；通过CAN总线采集相关的车辆信息并反馈到人机交互界面进行保存和下载；采用电线直接相连的方式从底盘测功机控制系统获取车辆实时速度，并反馈到人机交互界面进行在线显示。

2 电动车驾驶机器人控制方法设计

所设计的电动车驾驶机器人控制方法如图2所示。

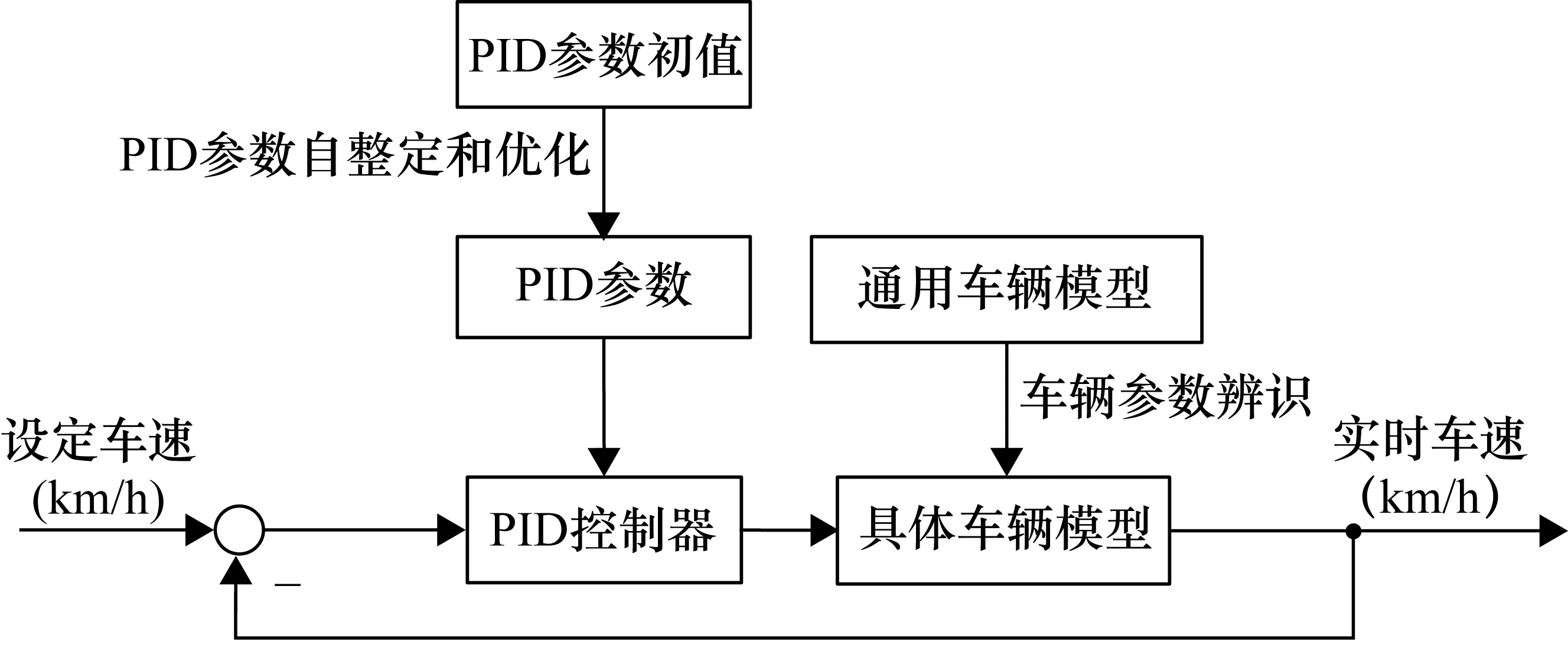
图2 电动车驾驶机器人控制方法

首先根据电动车动力学模型、传动模型和电机模型建立输入为加速踏板开度、输出为车辆速度的电动车整车通用模型；其次，针对通用车辆模型中的未知参数，采用非线性最小二乘法进行车辆参数辨识得到具体的车辆模型；最后，选定合适的PID控制器参数初值，采取粒子群算法实现PID参数在线自整定和以及参数优化，将得到的PID控制器作用于车辆模型，保证了对给定车速的跟踪控制精度[3]，使得模型输出的车辆速度准确跟随任意设定工况。

2.1 电动车控制模型

所设计的电动车转毂驾驶机器人通过加速踏板开度实现对于车辆速度的控制，因此所建立的控制模型需体现加速踏板开度与车速之间的数学关系，控制模型分为车辆纵向动力学模型、传动系统模型、电机模型3个部分[4]。

根据车辆模型结构建立车辆纵向动力学模型[5]，如式(1)所示。

(1)

式中，J为转动惯量(kg·m2)；Te为作用在驱动轴上的力矩(Nm)；w为车轮角速度(rad/s)；r为车轮半径(m)；Fx为地面提供的摩擦力(N)。

设定电机期望力矩最终得到电机输出力矩并作用于驱动轴，分析电机系统力矩的输入、输出特性，建立如式(2)所示的电机模型[6]。

(2)

式中，τ为一阶系统的时间常数。

电机的输出力矩为Tl，经减速器，作用于驱动轴的上驱动力矩为Te，电机的输出力矩和驱动力矩满足：

Te=R×Tl

(3)

式中，R为减速比。

综合式(1)～式(3)可得通用电动车模型如式(4)和式(5)所示[7]。

(4)

(5)

其中，

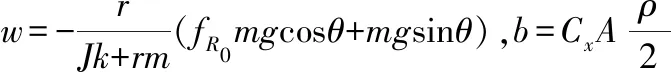
式中，v为车辆速度(m/s)；m为电动车质量(kg)；Cx为车辆形状特征的空气阻力系数；A为迎风面积(m2)；ρ为空气密度(Ns2m-4)；k为车轮半径的倒数(m-1)；Treq为电机期望扭矩；θ为转毂试验道路坡度(°)；fR0、fR1、fR2为滚动阻力系数，均为常数。

由试验采集数据可知电动车加速踏板开度S和期望扭矩Treq之间的关系为

S=q×Treq

(6)

式中，q为比例系数。

将加速踏板开度和期望力矩之间的关系S=q×Treq代入到式(5)中，并且电动车的输出力矩对期望力矩的跟随迅速，因此可以认为式(5)中时间常数近似为零，期望力矩近似等于输出力矩，因此由式(3)、式(6)所得加速踏板开度S和驱动力矩Te之间的关系为

(7)

将式(7)带入到式(4)，由此可以得到本文电动车通用车辆模型：

(8)

式(8)为输入为加速踏板开度、输出为电动车车速的通用电动车模型，用来模拟实际电动车用转毂驾驶机器人控制进行转毂试验，实现对设定工况的准确跟随。

2.2 模型参数在线辨识

为了使得电动车通用模型和实际车辆进行匹配，要对电动车进行在线参数辨识，式(8)中转毂试验道路坡度θ、滚动阻力系数fR0、fR1、fR2分别通过转毂按照试验要求进行设定；电动车质量m、电动车车速v、电动车加速踏板开度和期望力矩Treq是通过测量得到的；比例系数p是通过计算得到。因此本文针对式(8)中的未知参数b、转动惯量J、车轮半径r，采用非线性最小二乘法实现车辆参数的在线辨识，已知模型参数取自一款实际的电动汽车，如表1所示。

表1 电动车模型参数

非线性最小二乘法是系统辨识中最基本的方法[8]，它具有系统先验统计知识少、算法简单、计算量少、收敛性好等特点。非线性最小二乘法一般可描述为

(9)

式中，r(x)=(r1(x),r2(x),…,rm(x)),ri:Rn→R,i=1,2,…,m(m≥n)。

采用高斯-牛顿法即用泰勒级数展开的线性项来近似构建的非线性模型，然后用线性最小二乘法估计参数，再通过迭代法得到满足方程(9)的一个解。

设非线性模型为F(Zi,x)，x=[x1,x2,x3]T表示非线性模型中的估计参数，使得x1=b,x2=J,x3=r，z=[z1,z2,…,zP]T表示自变量S，v表示因变量，Zi，Vi为观测值，i=1,2,…,m，如式(10)所示。

ri=vi-F(zi,x),i=1,2,…,m(m≥n)

(10)

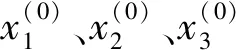
(11)

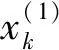
2.3 控制器PID自整定

PID控制器可以通过调整Kp、Ki和Kd三个参数使系统的控制性能达到预定的要求。因此在PID控制器的设计过程中，对控制参数的有效整定是关键。手工整定法建立在经验的基础上，在参数空间较大的时往往难以找到较优的结果；而其他参数整定方法也常因对象模型的不确定而难以得到参数的全局最优解。

采用粒子群(Particle Swarm Optimization,PSO)算法[9]进行PID参数自整定，该算法概念简明、实现方便、收敛速度快、参数设置少，是一种高效的搜索算法[10]，在工业和工程中的优化中得到广泛地应用[11-12]。

粒子群中每个粒子表示D维空间的一个解，则第i个粒子的状态Xi=(xi1,xi2,…，xiD)，它经历过的最好位置记作Pi=(pi1,pi2,…,piD)记作pbest，每个粒子的速度向量V=(vi1,vi2,…,viD)。群体经历过的最优状态记作gbest，对每一代来说它的第d维(1≤d≤D)根据如下方程进行变化：

(12)

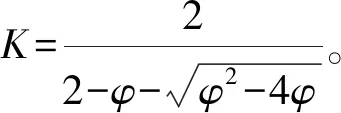
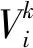
粒子i经过飞行将出现一个新的位置，新位置的计算公式为

(13)

粒子群算法中PID参数的搜索空间的确定采取与文献[13]相同的确定方式，即以ZN法获得的结果Kp、Ki、Kd为中心向左右拓展而形成的搜索空间。粒子在飞行过程中每个粒子将分别依据单子粒子的飞行经验和群体的飞行经验对飞行速度进行动态调整[14]，然后以一定的速度向目标逼近直至找到最优目标，即PID控制器的最优参数。基于粒子群算法的PID控制系统结构如图3所示。

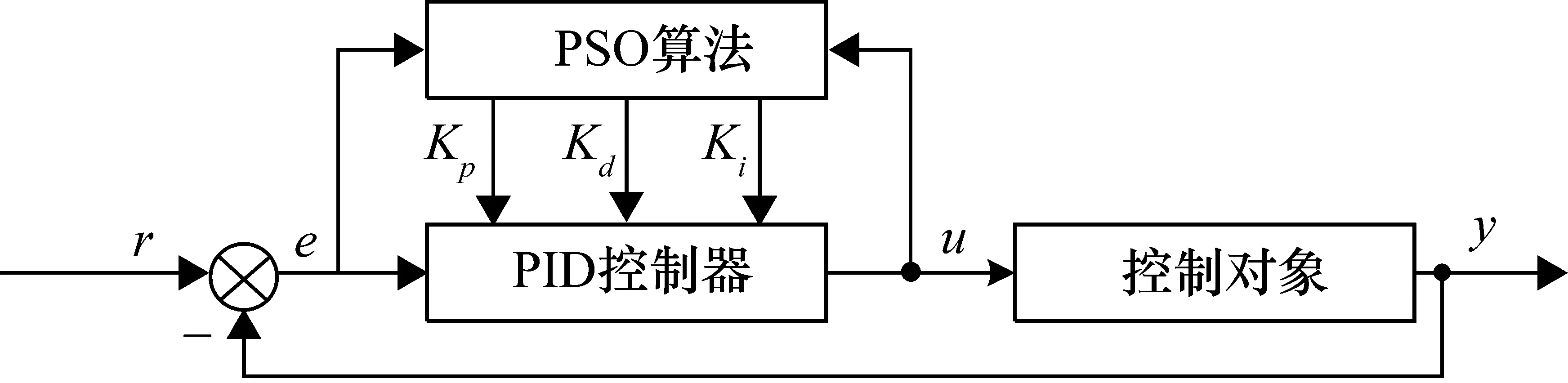
图3 基于粒子群参数优化的PID控制器

采用能反映系统调节品质的ITAE作为目标函数。由于PID参数寻优是求目标函数的极小值问题，因而要对目标函数进行改造，将极小值问题转换为极大值问题，则适应度函数取为

(14)

式中，e(t)为绝对误差。

PSO的各个参数为微粒数m=20，最大迭代数Gmax=40，φ1=2，φ2=3。

PSO算法用于PID参数自整定的算法流程如下：

① 设定粒子群算法所需要的初始条件，如微粒数、最大迭代次数和PID参数的搜索空间范围等；

② 随机产生粒子的初始位置和初始速度；

③ 分别计算每一个粒子所代表的性能指标ITAE函数值；

④ 判断系统是否稳定，进而得到粒子本身的最佳解和全部粒子的最佳解，更新粒子的位置和速度。

直到所设定的回路结束，便可得到一组最佳的PID参数。

3 试验结果分析

3.1 试验系统构建

为评估本文所提方法的性能，选择试验场四驱底盘测功机和转毂驾驶机器人进行试验，如图4所示。

图4 试验场地四驱底盘测功机

试验用到四驱底盘测功机、人机交互界面和驾驶机器人控制系统。底盘测功机控制系统模拟行驶路面载荷对汽车施加的各种阻力对车速控制带来的干扰；人机交互界面的安装设备为华硕5800电脑；驾驶机器人控制系统为倍福工业控制器CX1010系列；控制车辆试验型电动车。

3.2 车辆模型辨识试验

根据式(8)提出的车辆模型，以及利用非线性最小二乘法辨识得到的车辆参数，如表2所示。

表2 非线性最小二乘法辨识参数

以100%加速踏板开度作为核对数据集，将训练后得到的模型输出速度和实车采集的车辆速度做对比，验证模型参数辨识的正确性。训练后的电动车模型如图5所示。

所建立的电动车模型对新的数据有较好的泛化性，车辆模型和实际电动汽车的时间-车速关系曲线误差控制在1%的范围内，满足转毂试验的要求。

3.3 PID参数整定试验

根据车辆模型(式(8))，输入为加速踏板开度，输出为车辆速度，依托现有的车辆模型采用粒子群算法实现PID参数在线自整定，通过PSO算法计算得到最优的PID参数。求得的PID参数如图6所示。

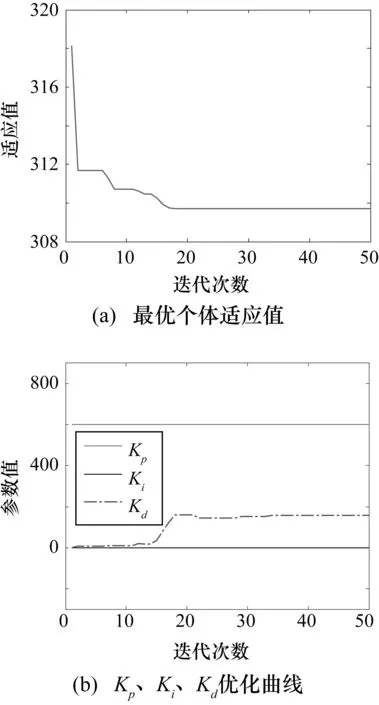
图6 适应度函数值和PID参数变化效果图

在PSO算法的计算优化过程中，随着迭代次数的增加，适应度函数值不断减小，最终趋于一个较小的稳定值，即得到PID控制器的最优参数。

根据手动整定PID参数的方法，求出的一组PID参数为Kp=556,Ki=0,Kd=165。

利用这两种方法整定出来的PID参数分别对电动车车速进行PID控制，验证跟随效果。

3.4 续驶里程试验

在预设工况下分别使用人员和驾驶机器人完成车辆操作进行续驶里程试验。驾驶机器人驾驶车辆进行试验采用两种不同的PID参数整定方法，即PSO整定方法(方法1)和手动整定方法(方法2)，跟随效果如图7所示。

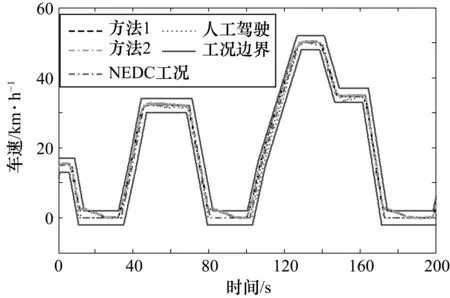
图7 人工驾驶和驾驶机器人试验效果对比图

人工驾驶电动车进行车辆试验，车速波动较大，且稳定性较弱；基于方法2的车速控制效果使得车速跟踪误差在±2 km/h 范围内，但在加速和匀速段最大误差较大，精度不够高；基于方法1的控制，抗干扰能力强，能够及时抑制干扰引起的车速变化，保证驾驶机器人系统的车速跟踪控制精度；与人工驾驶相比，PID控制均具有突出的优越性。而基于方法1即粒子群算法的PID整定方法的跟踪效果更好，精度更高。

选择NEDC工况中四次城市循环的第一次加减速工况作为对象对比驾驶机器人方法1和方法2以及人工驾驶的加速踏板控制平滑性，对比结果如图8所示。

人工驾驶的加速踏板开度毛刺较多，平滑性差；基于方法2的加速踏板开度相比于人工驾驶有很大的改善，但是在匀速段，加速踏板开度仍有明显振荡；基于方法1的加速踏板开度控制平稳，平滑性明显优于人工驾驶和方法2。

从表3中可以看出，人工驾驶的出错次数为3，方法1与方法2出错次数为0，方法1的平均误差与最大误差都比方法2低，误差最小，证明了方法1的有效性与优越性。

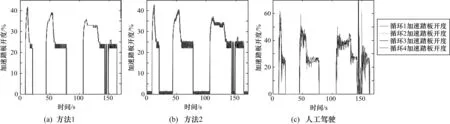
图8 驾驶机器人驾驶与人工驾驶加速踏板开度图

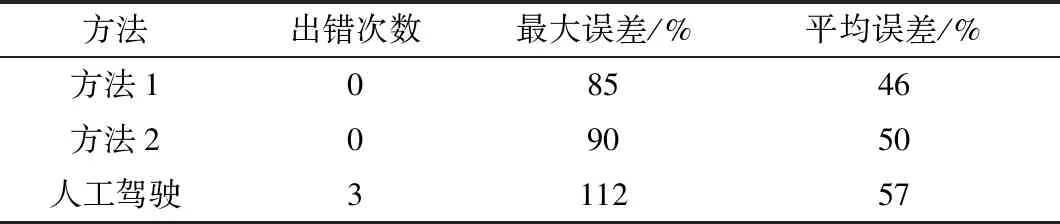
表3 驾驶机器人与人工驾驶速度跟随效果统计数据

选择NEDC工况中的第一次城市循环作为对象对比驾驶机器人驾驶方法1和方法2以及人工驾驶加速踏板控制重复性。以循环1的加速踏板开度作为对比数据，分别以循环2、循环3、循环4的加速踏板开度和循环1的加速踏板开度做方差，统计数据如表4所示。

由数据可知人工驾驶的加速踏板开度方差的平均值远远大于基于方法1和方法2加速踏板开度方差的平均值，随着循环次数的增加，人工驾驶的加速踏板开度方差明显增加，而基于方法1和方法2的加速踏板开度方差基本保持一个较小值稳定；对于方法2，随着循环次数的增加，加速踏板开度方差增长较多，即随着试验次数的增多，控制效果逐渐变差；而对于方法1，随着循环次数的增加，加速踏板开度增长不明显；所以，基于方法1的驾驶机器人驾驶的重复性大大优于人工驾驶和基于方法2的驾驶机器人驾驶。

4 结束语

基于通用电动车模型提出了一种非线性最小二乘法，完成车辆参数的在线辨识，得到具体的电动车模型。针对具体的电动车模型提出了一种PID控制方法，设计粒子群算法实现PID参数自整定和参数优化。驾驶机器人的PID控制方法实现了加速踏板开度的平滑控制以及对设定工况的准确跟踪，使得转毂试验的可重复性高。试验结果验证了本文提出的理论和方法的有效性和可行性。

驾驶机器人完全能够代替人类驾驶员完成各种高重复性和长时间的汽车试验，适用于电动车的续驶里程试验。