基于颗粒接触理论的岩石压密阶段本构模型

2019-09-18马秋峰秦跃平周天白杨小彬

中南大学学报（自然科学版） 2019年8期

马秋峰，秦跃平，周天白，杨小彬

(中国矿业大学(北京)应急管理与安全工程学院，北京，100083)

砂岩是最重要的油气储集层，世界上大部分的油气资源都储存在砂岩中。此外，砂岩中常常有煤和各种金属矿床。因此，对于砂岩力学性质的研究具有重要的意义。由于砂岩内部结构的特殊性，传统Hooke模型不能准确地描述其应力-应变关系，其原因如下：砂岩存在压密阶段，岩石表现出非线性特征；砂岩具有塑性硬化和软化现象，同样表现出非线性特征。人们对砂岩的力学性质进行了大量研究，发现砂岩的强度受到孔隙率的影响，孔隙率越高，砂岩的强度越低[1-3]。同时，砂岩屈服面、硬化函数、塑性变形同样受到孔隙率的影响[4-8]。BAUD等[6]分析了不同孔隙率下岩石的单轴抗压强度，提出了影响岩石强度的含孔隙翼型裂纹模型。KULHAWY[7]认为随着孔隙的压密，弹性模量迅速增大。AL-HARTHI 等[8]分析了孔隙率对岩石弹性模量的影响，并建立了考虑孔隙影响的弹性模量模型。ZHAO 等[9-10]提出了各向异性应力条件下多孔岩石的三维模型，在该模型中，一部分孔隙内的变形用基于自然应变的胡克定律描述，另一部分孔隙内的变形用基于工程应变的胡克定律描述。李连崇等[11]完善了上述模型，并利用该模型实现了FLAC3D开发。王青元等[12]将岩石峰前变形阶段分为2个部分，分别建立了本构模型。曹文贵等[13-14]在统计损伤模型的基础上，采用宏观与微观相结合的方法，将空隙岩石分为岩石骨架和空隙2个部分，建立空隙岩石变形分析模型；该模型不仅反映了空隙岩石的应变软化特征，而且还反映了空隙岩石在初始压密阶段的变形非线性特点。近年来，人们从颗粒接触入手，对砂岩的力学性质进行分析。LESZCZYNSKI[15]利用颗粒的接触黏聚力，模拟颗粒材料的动载过程。NASSAUER 等[16]提出了多面体颗粒接触计算方法。FENG[17]提出了非圆球形接触模型的计算方法，为离散元计算提供了接触模型。袁康等[18]对岩石压缩荷载作用下内部颗粒组分的力学响应进行了研究，从细观层面揭示了岩石的破裂机制。目前，有关砂岩的压密阶段以及砂岩颗粒接触的研究较多，而通过接触理论来描述岩石压密阶段的本构关系的研究较少。本文作者以颗粒接触为研究基础，认为岩石压密阶段中碎屑颗粒之间的孔隙也被压密，并且岩石压密阶段非线性特征与颗粒间的接触有关。通过引入G-W接触模型，建立接触元件模型用于表征岩石中碎屑颗粒的接触，同时采用弹簧元件表征颗粒本身的线弹性特征，将二者串联，用于描述岩石压密过程中的应力-应变关系。利用建立的串联模型计算岩石压密阶段的本构关系，并与实验结果进行对比以验证模型的合理性。

1 接触模型的建立

在沉积学中，根据砂岩内部结构，砂岩主要由碎屑颗粒、杂基、胶结物和孔隙这4个部分组成。其中杂基和胶结物又合称为填隙物。根据砂岩内部碎屑颗粒数量的不同，砂岩的承载形式主要分为2类：颗粒承载和杂基承载。本文主要研究碎屑颗粒数较多的颗粒承载。CHEN等[19]认为，在成岩过程中，岩石存在压溶作用，岩石中碎屑颗粒之间呈现凹凸状的接触。由于颗粒间凹凸体的存在，岩石在初始加载过程中呈现出非线性特征。

在描述压密阶段的本构关系时，传统本构模型[7-10]往往采用孔隙率作为内变量来描述岩石的应力-应变关系。尽管模型在一定程度上能够描述压密过程，然而此类模型只能反映出压密阶段一部分力学行为，并没有从岩石压密过程的机理上反映出岩石的非线性变形规律。例如，模型没有考虑压密过程中渗透方向等问题。

本文作者通过分析沉积学中关于砂岩压密阶段的承载规律，提出利用颗粒间不平整接触面作为本构模型的建模基础。首先建立能够反映颗粒间不平整接触的元件模型，然后利用该元件模型建立岩石压密阶段本构模型。从模型结构来看，本文提出的模型更加简洁，同时物理意义更加明确。

传统的元件模型在岩石力学行为研究中得到了广泛应用。其中，经典西原正夫模型(Nishihara model)被广泛应用于描述岩石蠕变特性。西原正夫模型示意图如图1所示。该模型主要包括弹簧元件、黏壶元件以及塑性元件。人们在元件模型的基础上，提出修正原正夫模型或者新的模型[20-23]，但用于描述岩石压密阶段的模型还未见报道。本文作者基于上述颗粒接触理论，在G-W 接触模型的基础上，提出岩石压密阶段的元件模型，用于描述岩石的本构关系，如图2所示。

由图2可知：该元件存在一个倾斜面，在该倾斜面上存在满足赫兹接触理论的凸起，且凸起高度满足正态分布。2个接触面之间的平均距离为d0(即接触面之间的张开度，简称张开度)。接触面与垂直方向的夹角为φ(简称接触面倾角)。接触面法向方向的力-位移关系可以采用G-W 模型进行计算。同时假设该元件宽度和厚度均为1 m。由于颗粒之间接触面的角度是随机的，并没有固定的方向，因此，接触面倾角φ用可于描述大量接触面接触方向的整体效果。

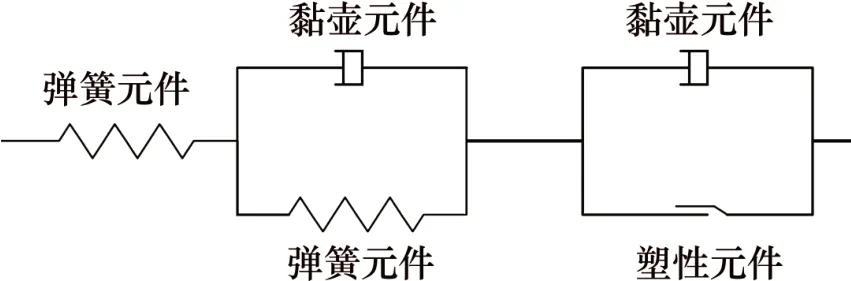
图1 西原正夫模型示意图Fig.1 Diagram of Nishihara model

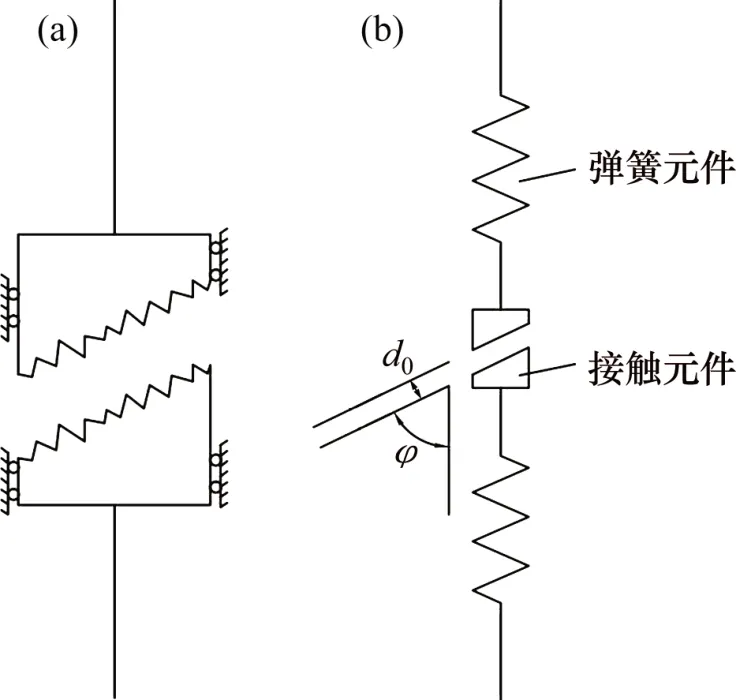
图2 压密阶段本构关系的元件模型Fig.2 Element model in compaction stage

接触元件模型用于描述压密阶段颗粒间的接触效应。此外，假设颗粒本身满足线弹性特征。为了表征颗粒本身的变形规律，在接触元件上串联1个弹簧元件(见图2(b))。

由于压密阶段往往应力较小，本文假设碎屑颗粒不发生塑性变形，即颗粒一直处于弹性状态；由于碎屑颗粒之间存在一定的黏聚力，因此，假设接触面不发生相互滑动，仅考虑接触面的法向作用力。

2 G-W模型简介

经典G-W 模型用于描述颗粒间接触面的相互作用。G-W 模型中，粗糙表面被描述为一系列凸起的组合，凸起之间通过赫兹定律进行计算。

G-W 模型假设如下：1)粗糙面剖面凸起的高度服从正态分布；2)凸起顶端具有相同的曲率；3)凸起变形相互独立，互不影响；4)忽略凸起下部的体积变化。

2.1 G-W模型中的粗糙度与概率密度

G-W 模型中的粗糙表面示意图如图3所示。图中，z(x)为在长度lc范围内横坐标为x处的高度。剖面粗糙度均方根ω(简称粗糙度)表示粗糙表面顶点高度与粗糙表面平均高度差值的标准差，其表达式为

G-W 模型中粗糙面的概率密度示意图如图4所示。图中，黑色区域表示高度大于z的凸起的概率。概率密度函数ϕ用于描述剖面某点处高度的概率分布。若以粗糙面平均高度为基准，在高度为(z,z+dz)范围内出现凸起顶点的概率为p(z，z+dz)，则概率密度函数ϕ(z)为

在G-W 模型中，认为粗糙面凸起高度满足正态分布，其概率密度为

图3 粗糙表面示意图Fig.3 Diagram of surface roughness

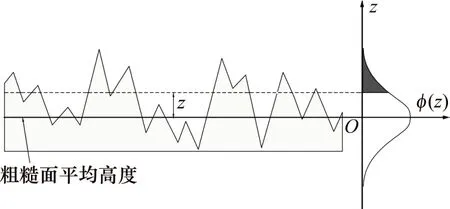
图4 粗糙面概率密度的求解示意图Fig.4 Schematic map for probability density solution of rough surface

2.2 粗糙面之间的接触分析

2个不同粗糙度的平面相互接触问题可以等效为刚性平面与可变形的粗糙平面相互接触的问题。等效后平面的粗糙度ωe可用等效前2 个平面的粗糙度表示：

式中：ω1和ω2分别为2个接触面的粗糙度。

将研究对象取为高度为zs的凸起(zs为高于粗糙面平均高度)。当刚性平面与粗糙面平均高度平面的距离为d时：1)若d＞zs，则凸起与刚性平面不接触；若d＜zs，则凸起与刚性平面相互接触，两者相互重叠的量为zs-d。根据赫兹定律，凸起与刚性平面的接触力f(zs)为

式中：E为凸起的弹性模量，β为凸起的曲率。与刚性平面接触的所有凸起的概率prob(zs＞d)为

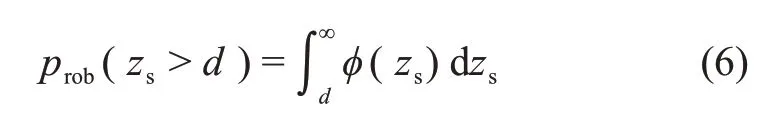
因此，单位面积上产生的接触力P(d)为

式中：N为接触凸起的数量。为了便于计算，假设当接触面位移为0 mm时，接触产生的压力近似为0 N。转化坐标后的接触面示意图如图5所示。以接触面零位移为坐标原点，凸起的平均高度距离起始点的距离视为张开度d0。根据式(7)转化坐标后可得位移为ln时接触面的法向力P(ln)为

由于颗粒间存在黏结物，忽略剪应力对接触面的影响。当一个斜向力作用在接触面时，假设只考虑法向分量对截面的影响。由于本文重点研究压密阶段岩石的本构关系，故暂未考虑当剪应力较大时接触面滑移以及岩石破坏的问题。

图5 转化坐标后的接触面示意图Fig.5 Schematic diagram of contact surface after coordinate transformation

3 压密阶段本构关系

3.1 组合元件的本构关系

当元件两端产生压缩量l后，令弹簧体的竖直方向位移为l1，接触体的竖直方向位移为l2，则有

弹簧中的力P1为

式中：k为弹性系数。根据几何关系，接触体的法向位移ln为

接触体的接触力P(ln)计算公式见式(8)。

对接触力进行分解，得到接触元件在竖直方向的力P2为

根据串联结构，令P1=P2，联立式(10)和(12)，计算得到压缩量l后组合元件中的力。已知模型尺寸后，便能够计算得到应力-应变关系。

通过上述关系，可计算得到在任意压缩量下组合单元中的力。为了求解组合单元中的应力-应变关系，需要定义每个元件的宽度与高度。已知岩石颗粒的弹性模量为Es，则弹簧的弹性系数k为

式中：S为元件所代表的岩石水平方向的截面积，此处为单位面积；h为元件中弹性部分的高度。

对于任意元件，

式中：h0为元件高度，此处取为1 m。

3.2 二分法在计算本构关系中的应用

式(8)是反映接触元件力-位移关系的重要表达式，但无法对其进行积分求解。本文采用数值计算的方法，计算得到近似解。由组合元件的力-位移关系可得：

假设总压缩量l已知，求解组合元件的受力。采用二分法进行数值计算，如图6所示。

首先将l分为两等分(见图6(a))，令l1=l2=l/2，假设此时弹簧元件中的力F1大于接触元件中的力F2，这说明弹簧元件的压缩量过大，需进行下一步修正。将图中AB段进行等分(见图6(b))，此时令l1=l/4，l2= 3×l/4。若此时F1＞F2，则等分左侧AD段，令l1=l/8，l2= 7×l/8；若F1＜F2，则等分DB段，令l1= 3×l/8，l2= 5×l/8；若此时F1=F2，则说明原假设l1=l/4，l2= 3×l/4 就是此时压缩量分配的计算结果。

依照上述方法，不断进行划分，直到达到计算的精度要求，即|F1-F2|＜R0(其中R0为精度判断参数)。

图6 二分法在计算过程中的应用Fig.6 Application of dichotomy in calculation process

3.3 侧向压力对压密过程的影响

本文第3.1 节中的受力分析过程仅考虑在单轴压缩条件下的本构关系，下面将分析侧向压力条件下的本构关系。

首先对元件施加侧向压应力，然后再施加竖直方向的位移。通过侧向压力计算得到接触面上的侧向力Pc，然后计算得到侧向压力在接触面产生的法向初始位移。在接触面法向存在预压力：

此后，施加竖直方向的位移。假设接触元件竖直位移为Δl2，此时接触面的法向位移ln为

通过式(8)计算得到法向接触力P(ln)，此时因竖直位移产生的力P2为

联立P1=P2，当l已知时即可计算得到单个组合元件的力。在已知模型尺寸后，便能够计算得到应力-应变关系。

4 模型的验证

下面验证模拟孔隙压密阶段岩石本构关系的元件模型的合理性。本文模型的参数主要包括颗粒的弹性模量E、单位面积凸起的数量N、凸起的曲率β、接触面的张开度d0、接触面粗糙度ω和接触模型中的倾角φ。

本文选取4 种不同孔隙率砂岩的实验结果[24-25]进行对比。由于文献[24-25]中没有给出具体的模型参数，本文参考文献[26-27]中微观砂岩颗粒的观察结果，推测出4种岩石的参数，如表1所示。由于孔隙率是确定颗粒间的张开度d0的重要参数，因此也列于表1中。由于对称性，颗粒之间接触面倾角φi的范围为[0°，90°]。对于颗粒接触面分布较为均匀的岩石而言，接触模型中的倾角φ可以通过求解倾角φi的数学期望得到，φ= 45o。

利用MATLAB数值计算软件对模型进行编程后，模拟得到模型压密阶段的应力-应变关系。不同砂岩本构关系的实验结果与数值模拟结果对比如图7所示。图7中，R2为模型对实验结果的拟合优度。

从图7可以看出：在岩石压密阶段本构关系表现出明显的非线性特征。在初始加载过程中，岩石应力增长较为缓慢，随着轴向位移的增大，应力增长速率逐渐趋于稳定。对比图7(a)和图7(c)可知：绿砂岩的压密阶段对应的应变范围为0～0.1%，Boise砂岩的压密阶段对应的应变范围为0～0.23%，这说明对于不同岩石材料，压密阶段对应的应变范围不同。

本文模型对绿砂岩的拟合优度为0.984，对Berea砂岩的拟合优度为0.991，对Boise砂岩的拟合优度为0.972，对Fontainebleau 砂岩的拟合优度为0.978。本文模型对实验结果模拟过程中，拟合优度均大于0.95，能够较准确地描述岩石在压密阶段的非线性变形规律，证明了模型的合理性。

利用Fontainebleau砂岩的模型参数，对不同侧向压力条件下进行压缩模拟，模拟过程中分别采用0，5，10，20和30 MPa的侧向压力。

表1 模型参数Table1 Model parameters

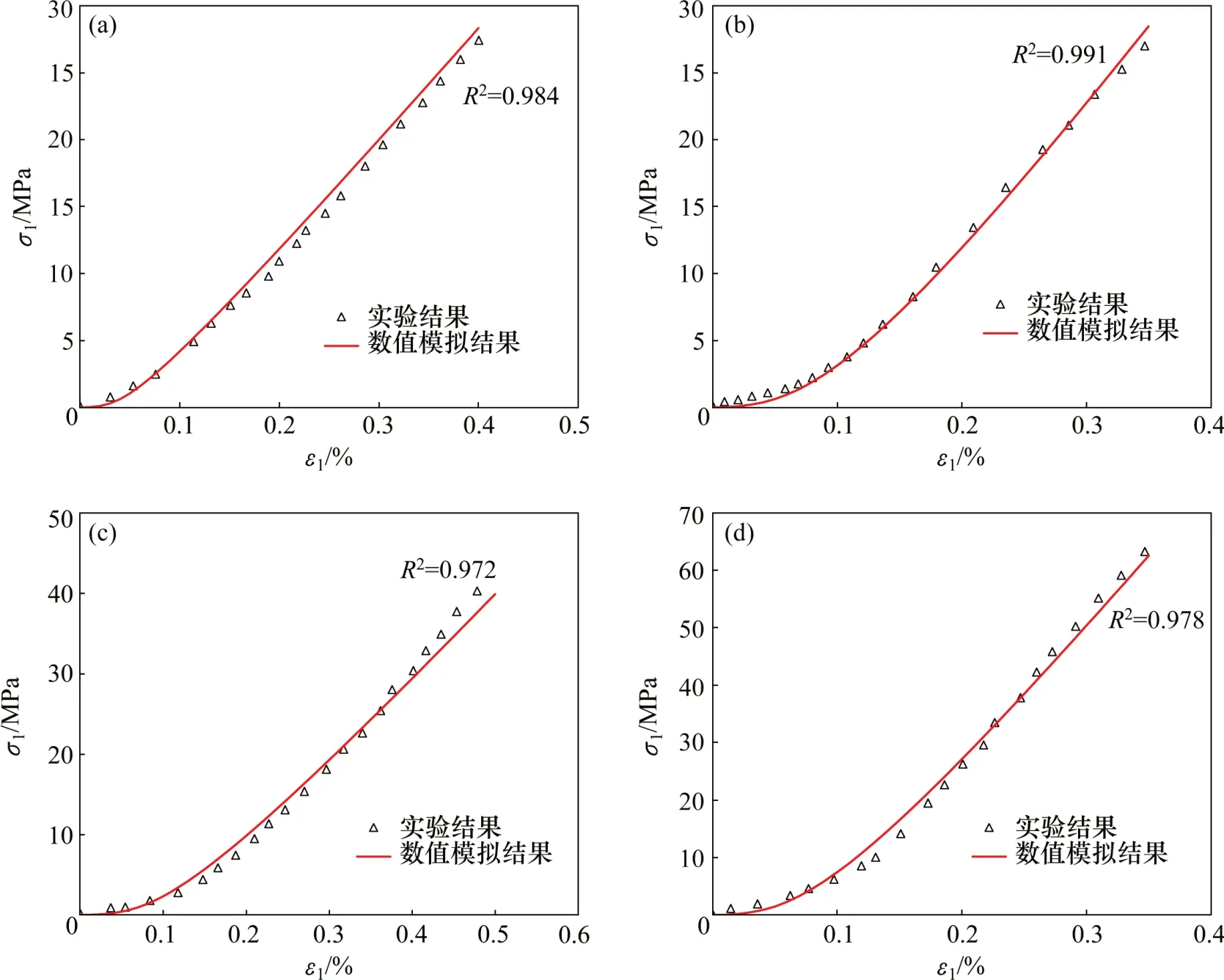
图7 不同砂岩本构关系的实验结果与数值模拟结果对比Fig.7 Comparison of experimental results and numerical simulation results for different sandstone constitutive relations

模拟的加载过程如下：首先施加侧向压力，垂直方向位移清零后施加垂直压缩位移。图8所示为位移过程中竖向的应力σ1和应变ε1的关系。

图8 不同侧向压力条件下压密阶段的应力-应变关系Fig.8 Stress-strain relationship in compaction stage under different lateral pressure conditions

从图8可以看出：在不同侧向压力的情况下，随着侧向压力的增大，初始压密阶段σ1增长的速率越快。当侧压力接近30 MPa时，应力-应变曲线趋近于线性。由此可见，数值模拟结果反映了岩石压密阶段的变形特点，与实验规律基本一致，这说明模型具有合理性。

5 模型参数分析

5.1 接触面粗糙度ω对压密阶段的影响

首先对接触面粗糙度ω进行分析。在本模型中，粗糙度ω表示接触表面凸起高度距离平均高度的离散程度。不同粗糙度的表面如图9所示。由图9可见：表面1的离散度更高，因此表面1的粗糙度更大。

取不同粗糙度ω在无侧向压力的条件下进行数值计算，计算结果如图10所示。

从图10可以看出：当粗糙度较小时，随着应变的增大，应力增长较快；当粗糙度较大时，应力增长的速率较慢。这与接触面中凸起的接触密切相关，当ω较小时，说明发生接触的凸起数量迅速增加，导致应力快速增长。

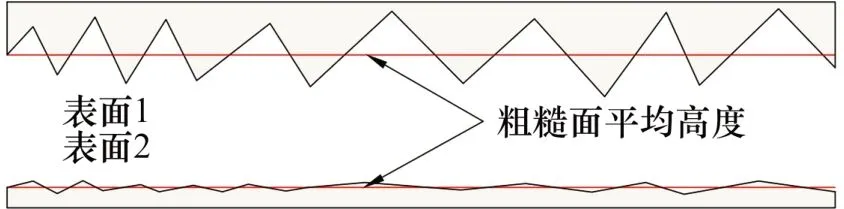
图9 不同粗糙度的表面Fig.9 Surfaces with different roughness

图10 不同粗糙度条件下的应力-应变关系Fig.10 Stress-strain relationship under different roughness conditions

5.2 接触面的张开度d0对压密阶段的影响

张开度与岩石的孔隙率紧密相关。通过表1与图7的计算结果可以看出：当岩石孔隙率较大时，需采用较大的张开度才能得到较好的数值计算结果；当岩石孔隙率较小时，需采用较小的张开度才能得到较好的数值计算结果。

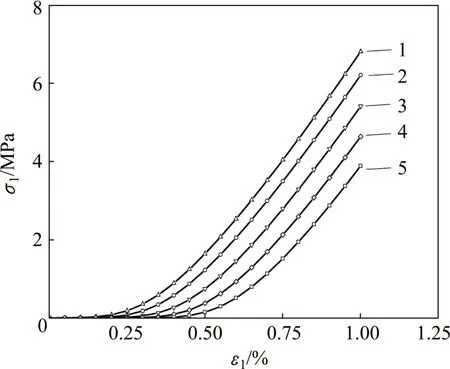
图11 不同张开度条件下的应力-应变关系Fig.11 Stress-strain relationship under different opening conditions

取不同张开度d0在无侧向压力的条件下进行数值计算，计算结果如图11所示。从图11可以看出：当张开度较小时，在经历较小的应变后，应力迅速增大；当张开度较大时，在经历较大的应变后，应力才开始逐渐增长。张开度d0综合反映了压密过程的长短，当张开度较大时，需要经历较长的压密过程，而小的张开度只需要经历较少的压密过程。