翼缝形状对垂直轴风力机翼型气动性能的影响
2019-09-18张立军马东辰顾嘉伟江奕佳米玉霞赵昕辉王旱祥刘延鑫刘静
张立军,马东辰,顾嘉伟,江奕佳,米玉霞,赵昕辉,王旱祥,刘延鑫,刘静
(中国石油大学机电工程学院,山东青岛,266580)
风力发电机按照主轴相对于地面的安装位置可分为水平轴风力机和垂直轴风力机。垂直轴风力机(VAWT)以无需偏航系统、机械机构简单等优点越来越受到人们的青睐,但由于其实际风能利用率远低于理论值,垂直轴风力机的大型化和商业化发展受到阻碍[1-2]。其主要原因是:风力机在旋转过程中,叶片攻角实时变化,当叶片处于大攻角工况下时,叶片表面的低压区会发生流动分离,导致翼型升力系数下降,阻力系数上升[3]。针对风力机风能利用率低的问题,人们对如何提高翼型升力、增大翼型升阻比进行了大量研究。20 世纪20 年代初期,CHEN 等[4-6]提出了开缝式机翼的概念。开缝问题的初步思想在于边界层控制,即通过对翼型附面层合理地吹气(或吸气),增加(或减少)能量,使得附面层分离延迟发生,解决大攻角下的失速问题[7-8]。目前,对于翼型开缝问题,国内外学者均进行了较多研究。COSOIU 等[9]利用数值模拟法,通过在试验中测试13种不同形状的翼型,利用空气动力学效应的叠加作用,增大小型风力机的体积流量,优化小型风力机壳体形状。BELAMADI等[10]利用二维仿真技术研究S809 翼型,讨论了缝隙宽度以及开缝倾角对翼型升阻比的影响,得到翼型较好的开缝方案。王龙等[11]通过计算流体力学方法对4种不同开缝位置风力机叶片进行数值模拟,获取了不同攻角下的叶片流场及升力系数,发现在大攻角下,开缝形成的射流能够较为有效地抑制流动分离现象发生,且开缝位置位于分离点附近时,气动性能较好。惠增宏等[12]利用测压法研究多段翼型前缘缝翼气动特性,通过对比不同构型缝翼对翼型增升效果和气动效率的影响,获得了较好的前缘缝翼方案。上述研究针对翼型开缝的特定问题都给出了相应的研究结果,但这些研究大都是集中在开缝位置和开缝角度上,对翼缝形状的研究较少,初步研究表明:翼缝形状对翼型气动性能有较大影响;同时,由于垂直轴风力机工况的特殊性,需要分风区来讨论开缝翼型的受力状况。目前所研究的翼型主要是集中在航天翼型和水平轴风力机翼型上,对垂直轴风力机翼型的研究鲜有涉及。为此,本文利用ANSYS FLUENT 软件,针对NACA0012翼型进行二维流体力学仿真,提出并对比不同开缝方案下翼型的升力系数和升阻比,得出给定条件下的最佳翼型开缝设计方案[13-14],同时,针对文中所研究垂直轴风力机翼型,提出分风区对称开缝的方案,以保证翼缝在不同风区对翼型气动性能具有提升作用。
1 模型与网格
1.1 模型及风力机主要参数
本文研究采用的翼型为对称翼型NACA0012,翼型的相关参数如表1所示。

表1 NACA0012翼型相关参数Table1 Parameters of airfoil of NACA0012
在大攻角下,气体在翼型吸力面尾缘处的动能远小于前缘处的动能,在尾缘处形成失速涡,发生附面层分离[15]。为提高气体在翼型吸力面动能,提出自下而上的开缝方案,导致翼型压力面部分气体由翼缝流经吸力面,加速吸力面气体的流动。考虑到直线形和弧形对气体流动产生的阻力较小,本文研究这2种形状的翼缝。首先根据弧形半径,提出3种弧形开缝方案,并按半径依次命名为T-8%,T-12%和T-16%,其中“8%”指弧形半径占弦长的百分比;然后讨论弧形与直线形相组合的翼缝形状对翼型气动参数的影响,根据不同的组合方案,将模型依次命名为T-double-arc(双弧形翼缝),T-arc(直线形与弧形组合式翼缝,迎风端形状为直线)和T-line(直线形翼缝),其中,常规翼型即未开缝翼型命名为T-0。表2所示为不同开缝下的翼型模型。
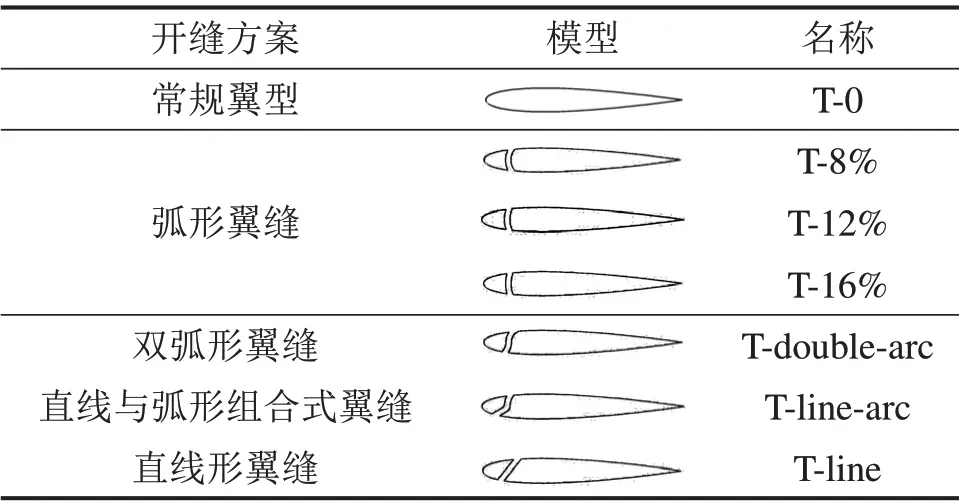
表2 不同开缝方案的翼型模型Table2 Airfoil model with different slotting schemes
1.2 网格划分
图1所示为计算域网格划分。由图1可见:计算域的上下边界长度为30 倍弦长,将弧形边界设置为速度入口,且距离翼型中心为15 倍弦长,翼型周边小圆直径为3 倍弦长。为减少翼缝对网格正交性影响,采用C-Y型网格。通过对翼型表面区域网格进行加密处理,确保近壁面处复杂流动的计算精度。网格示意图如图2所示。

图1 计算域示意图Fig.1 Calculation domain diagram
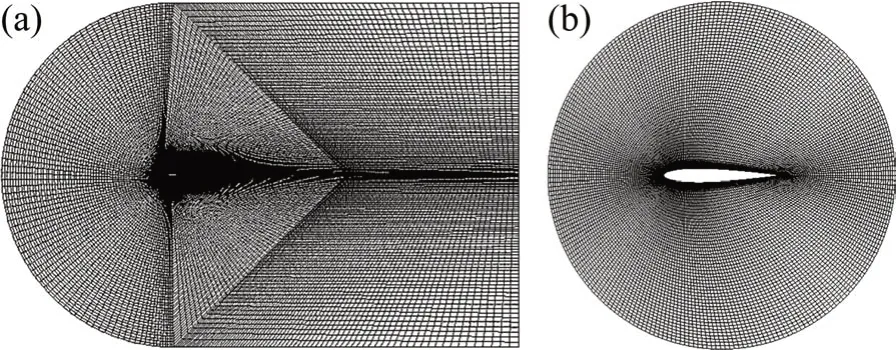
图2 网格示意图Fig.2 Grid diagrams
1.3 网格独立性验证
为确定仿真模型网格数目,减少计算步骤和提高网格精确度,在雷诺数Re为1.8×105,攻角α为10°的条件下,采用T-0翼型,针对网格数目对翼型升阻力系数的影响进行对比。表3所示为网格独立性验证结果。由表3可知:当网格数目为4.6×104时,翼型升力系数不再变化,且网格数目为4.6×104左右时,翼型阻力系数也非常接近,这表明计算结果不会再随着网格的加密而发生改变。因此,在以下研究中,针对不同开缝方案,通过对翼缝表面区域进行处理,将网格数目控制在4.6×104左右。
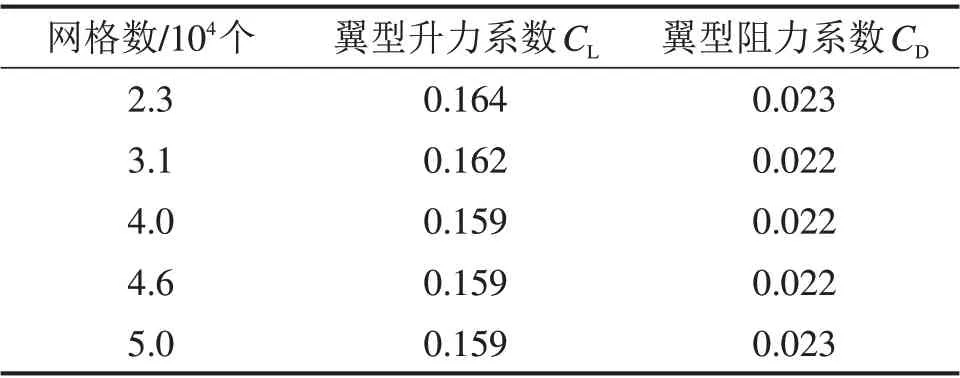
表3 网格独立性验证Table3 Grid independence verification
2 开缝位置的确定
为研究翼缝形状对翼型气动性能的影响,首先确定翼型的开缝位置。当开缝位置位于分离点附近时,能较好地延缓附面层分离,提高翼型的升力系数[11];而当翼型攻角增加到临界攻角时,翼型升力突然下降,阻力上升,附面层分离开始发生[16]。因此,需首先得到翼型在给定雷诺数下的临界攻角,在该临界攻角下,进一步求解翼型的附面层分离点。
2.1 临界攻角
研究发现,对于该外流场模型,SSTk-w模型能更好地反映流场的特征,得到的结果与试验结果吻合程度较高[17],因此,以下仿真均采用SSTk-w模型。对T-0 翼型进行二维流体仿真,改变攻角(取0°~20°)得到翼型的升阻力系数值和流线图,结果分别如图3和图4所示。由于本文主要研究不同方案下翼型气动参数的变化趋势,因此,在ANSYS 设置参考值时均选择默认值,所得到的升阻力系数也均为相对升阻力系数。
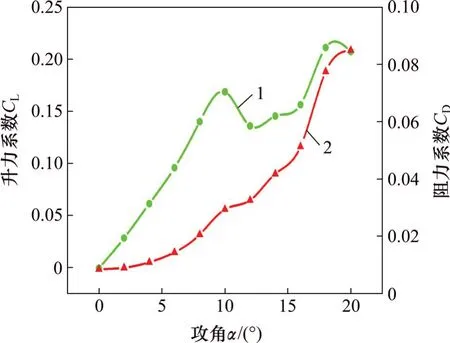
图3 T-0翼型升阻力系数Fig.3 Lift and drag coefficient of T-0 airfoil
由图3可以看出:当攻角α为10°时,翼型升力系数出现峰值;当攻角进一步增大时,翼型升力系数下降,这表明失速发生在攻角α超过10°之后。结合图4中4种攻角下的翼型流线图可知,当攻角α为10°时,翼型出现附面层分离的趋势;当攻角α为12°时,翼型上表面已经出现失速涡,而且随着攻角进一步增大,失速涡也逐步增大。结合图3可知,当α为11°时,翼型升力系数出现首次下降,因此,认为攻角α为11°时,附面层分离开始出现,翼型发生失速。
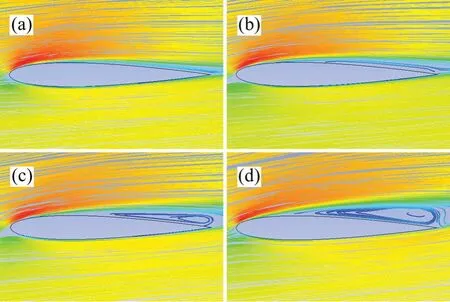
图4 不同攻角下T-0翼型流线图Fig.4 The streamline profile of T-0 airfoil under different attack angles
2.2 附面层分离点
在攻角α为11°时,对翼型T-0的气动参数进行分析,得到翼型表面的压力系数分布如图5所示。从图5可见:当翼型吸力面和压力面压差较大时,翼型能够获得较高升力,反之,翼型升力减小,气动性能下降[17]。因此,通过观察翼型表面的压力系数变化,便可得到附面层分离点的位置。
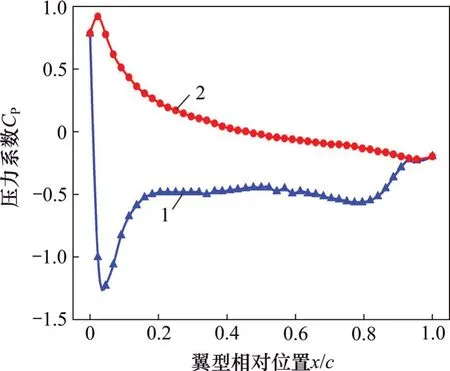
图5 T-0翼型表面压力系数分布图(α=11°)Fig.5 Airfoil surface pressure coefficient distribution of T-0 under partial attack(α=11°)
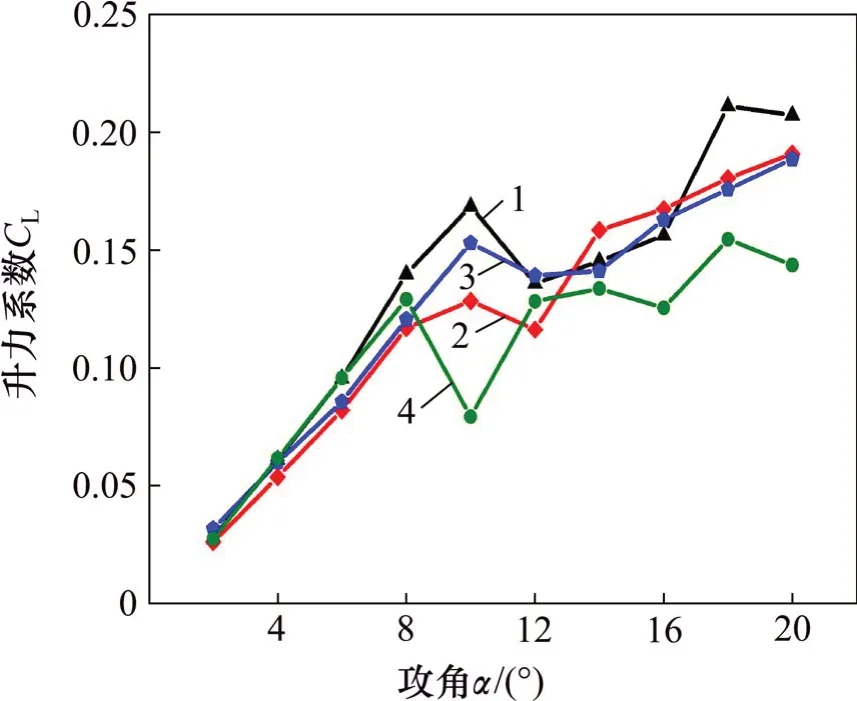
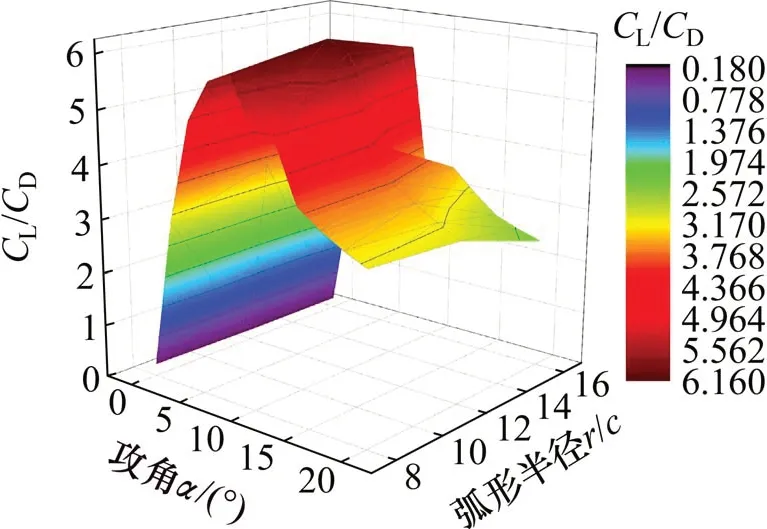
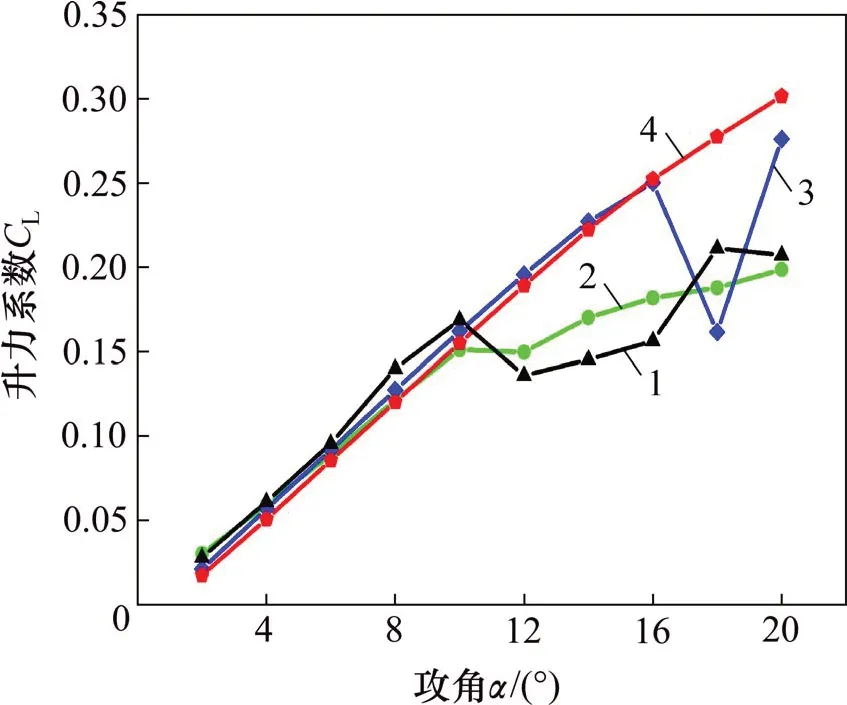
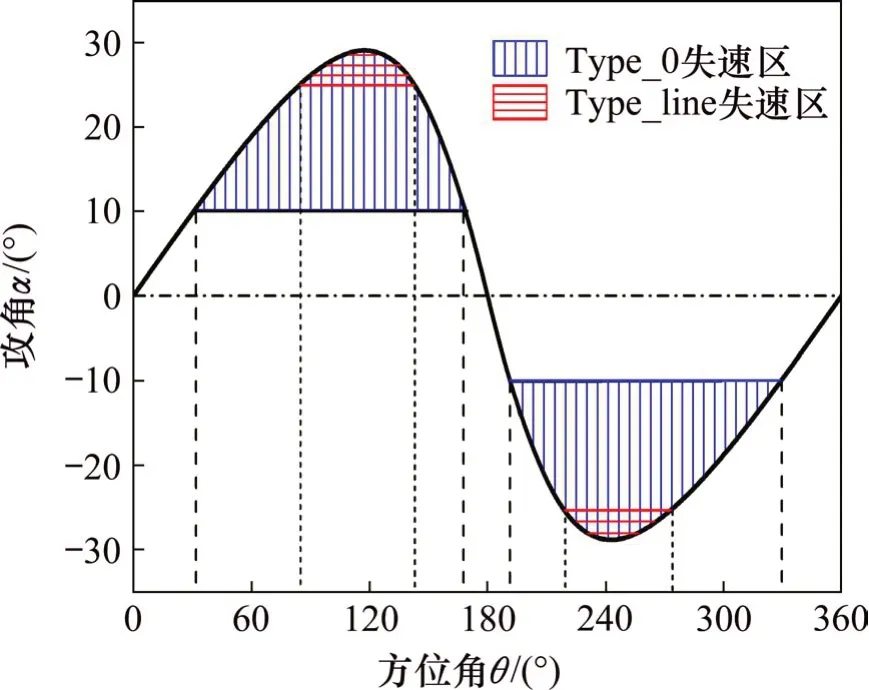
由图5可见:当翼型在x/c>0.05 时,翼型吸力面和压力面的压力系数差值开始迅速缩小,表明失速开始发生;当翼型在0.15 针对表2中6 种开缝方案,分2 组讨论,研究不同翼缝形状对翼型性能的提升作用。首先研究不同弧形半径的翼缝,然后利用最佳弧形与直线形相组合,得到最佳开缝方案。 按照翼缝半径占弦长之比,提出3种弧形开缝方案,即表2中T-8%,T-12%和T-16%,值得注意的是,能够实现弧形与翼型边界相切的最小半径在r/c在8%左右,所以,将T-8%看作是能够满足翼型开缝的最小半径方案。针对不同的弧形开缝方案,分别进行二维流体力学仿真,整理得到不同开缝方案下的翼型升力系数,如图6所示。 图6 不同弧形半径方案翼型升力系数Fig.6 Airfoil lift coefficient of different arc radius scheme 由图6可以看出:3 种弧形开缝方案对翼型升力系数的提升效果均不明显,开缝翼型对应的升力系数整体上比常规翼型的小,且随着弧形半径的增加,附面层发生分离对应的攻角变小,即翼型失速相对于常规翼型提前发生,说明弧形翼缝方案对延迟临界攻角起到的作用较小。 为观察弧形翼缝对延迟翼型附面层分离点的作用,得到翼型临界攻角附近的流线图,如图7所示。 图7 弧形开缝方案不同攻角下翼型流线图Fig 7 Streamlines of slotted airfoil under different attack angles 由图7可知:T-16%翼型在攻角α=10°时就已完全失速,翼型表面已经形成失速涡,相较于其他2种方案,其对翼型气动性能的提升效果最差;而T-8%和T-12%开缝方案在相同攻角下流线图非常接近,且对延迟附面层分离点都有一定效果,相较于图4,附面层分离点均有明显后移,这说明对于开缝翼型,压力面的部分气体通过翼缝吹向吸力面,增加翼型吸力面的气流动能,达到延迟附面层分离的效果。 考虑到开缝翼型改变升力系数的同时,也会使阻力系数发生改变。翼型升阻比是翼型升力系数与阻力系数的比值,升阻比越大,说明翼型在同一攻角下的升力系数远大于阻力系数,翼型的气动性能越好[18]。因此,为合理地选择最优弧形半径,通过对比不同弧形半径下各攻角所对应的翼型升阻比,来选择弧形翼缝的最佳半径。不同弧形半径下各攻角所对应的升阻比如图8所示。 由图8可知:当攻角α<10°时,不同弧形半径在同一攻角下对应的升阻比非常接近,在攻角α=10°时,弧形半径r=12%c的升阻比最大;当α>10°时,随着弧形半径变小,翼型升阻比变大,即翼型的气动性能更好。而要解决的翼型失速问题主要出现在大攻角下[19],因此,认为r=8%c为最佳弧形半径,即选择T-8%为弧形开缝方案的最佳翼型。 图8 不同弧形半径下各攻角所对应的升阻比Fig.8 Lift-drag ratio of attack angle under different arc radius scheme 由图7可知:弧形翼缝使翼型升力系数下降的主要原因是弧形翼缝的迎风端与气流方向呈负夹角,使得翼型压力面的气体在进入翼缝时受到一定阻碍,同时在翼缝内部形成环形气流,增加气流动能的损失。 为解决弧形翼缝迎风端与来流风速方向不匹配问题,通过改变弧形翼缝迎风端即气流入口方向得到以下3 种开缝方案,即表2中的T-double-arc,T-line-arc和T-line。同时,为减少翼缝倾斜角度对求解翼型升阻力系数带来的影响,在不同的开缝方案中,保证翼缝的两端相对位置不变。通过改变攻角,得到不同开缝方案下的翼型升力系数与升阻比曲线分别如图9和图10所示。 图9 不同组合方式翼型升力系数Fig.9 Lift coefficient under different combination types 图10 不同组合形式翼型升阻比Fig.10 Lift-drag ratio under different combination types 由图9可见:T-double-arc在翼型升力系数提升方面效果不佳,没能起到延迟临界失速攻角的作用。而T-line-arc和T-line对升力系数的提升较为明显,尤其在攻角α超过10°部分,翼型升力系数较常规翼型Type-0有了显著提高;在攻角α小于16°部分,T-line-arc和T-line对翼型升力的提升效果较为接近,但T-line-arc在攻角α大于16°后发生了失速,而T-line在攻角α小于20°未发生失速。通过进一步研究发现,T-line发生失速时的攻角为26°,说明T-line-arc和T-line这2种开缝方案在增大临界攻角方面都起到了较好的效果,且T-line的作用效果更好。 由图10可知:T-line-arc 在未发生失速之前,即攻角α小于16°,对翼型的气动性能提升有更好的效果,发生失速后,翼型的升阻比下降较为明显,而T-line 在所研究攻角范围内对翼型气动性能的提升作用更稳定。值得注意的是:当风力机工作在小攻角范围,即攻角α<10°时,对翼型进行开缝反而会降低翼型的气动参数,主要原因在于翼缝的存在增加了翼型表面对气流的阻力,这个问题可以通过加装翼缝开关来解决,即通过加装控制系统,在小攻角下关闭翼缝,大攻角下打开翼缝,使翼型的出力效果最优[10]。 为进一步观察翼缝形状对延迟附面层分离点的影响,得到大攻角下翼型的流线,如图11所示。由图11可知:3种开缝形式在延迟附面层分离和推迟失速涡形成方面都起到了较好的效果,其中,T-doublearc相较于其他2种形式效果较差,在攻角α=20°时形成了失速涡,而T-line-arc和T-line在所研究攻角范围内都未出现失速涡,对延迟附面层分离方面也都起到了较好作用。 开缝方案的选择与风力机旋转过程中所能达到的最大攻角有关,而最大攻角可由叶尖速比计算得到[20],当风力机运行工况的叶尖速比λ≥3.5 时,翼型旋转过程中叶片最大攻角不会超过16°,在该情况下,可选择T-line-arc 为开缝方案;当风力机工作在低叶尖速比下即λ<3.5 时,叶片攻角可以达到较大值,例如本文中叶尖速比λ=2.0,叶片攻角最大值可以达到30°,而T-line 开缝方案在大攻角下对翼型气动性能的提升有显著的效果,所以,在低叶尖速比下选择T-line为最佳开缝方案。 针对本文给出的开缝方案,以T-line开缝方案为例,得到其风轮旋转1周过程中叶片的位置图如图12所示。其中,θ为叶片方位角,当方位角θ位于(0°,180°]时,该区域称为风轮的上风区;当θ位于(180°,360°]时,称为风轮的下风区。 由于靠近来流风向的一面为压力面,当叶片位于上风区时,其外侧为压力面,而当叶片处在下风区时,其内侧为压力面[21]。观察图12可以发现:本文上述开缝方案中翼缝的方向仅适用于下风区,对于上风区,压力面的气流通过翼缝进入吸力面后,会使吸力面气流向翼型前缘流动,对于延迟附面层分离起到反作用。考虑到上下风区叶片攻角的对称性,其对翼缝的研究也是对称的,所以,对于垂直轴风力机翼型,提出在上下风区对称开缝的方法,翼型分风区开缝方案如表4所示。 图11 大攻角下不同组合形式翼型流线图Fig 11 Streamline profiles of different combinations at large attack angles 图12 风轮旋转一周叶片位置图Fig.12 Blade position in pace of the wheel rotation 按照表4所示分风区开缝方案,可保证风轮旋转1周过程中,压力面气流都可通过翼缝吹向翼型吸力面后缘,达到延迟附面层分离的目的。因此,对叶片进行对称开缝,通过加装控制装置,实现叶片处于不同风区时翼缝方向的改变。 表4 翼型分风区开缝方案Table4 Airfoil slit scheme in different windstream area 针对叶尖速比λ=2的情形,根据双制动盘多流管理论进行MATLAB 编程,得到风轮旋转1 周过程中叶片攻角随方位角呈类正弦变化规律[22]。由上述分析可知,常规翼型T-0 在攻角α≥11°时出现失速现象,而采用T-line开缝方案后,翼型的临界攻角出现了延迟;当攻角α≥26°时,翼型才进入失速状态。图13所示为翼型对称开缝前后叶片失速区范围示意图。 由图13可以看出:在风轮旋转1周过程中,常规翼型T-0 在方位角30º≤θ≤170º和190º≤θ≤330º时,攻角α≥11°,即叶片处在失速区的方位角范围高达77.8%;采用T-line开缝方案后,攻角α≥26°的方位角处于85º≤θ≤140º和220º≤θ≤275º附近,叶片发生失速的区域占整周的30.5%左右。因此,采用开缝翼型后,叶片失速区范围下降了61.5%,叶片在大部分工况下可以保持高升力系数。 图13 翼型对称开缝前后叶片失速区范围示意图Fig.13 Schematic diagram of the stall area of the blade before and after the symmetrical slotted is adopted 1)针对垂直轴风力机在大攻角下的附面层分离问题,提出了6种开缝方案,并进行网格独立性验证得到翼型划分网格的最佳数目为4.6×104个。 2)翼型的临界攻角α=11°,在该临界攻角下计算得到x=1/8c为理想开缝位置。 3)弧形开缝翼型在延迟翼型临界攻角上作用较小,但可有效推迟附面层分离点,同时以获得最大升阻比为研究目标,得到最佳的弧形半径r=8%c。 4)当叶尖速比λ≥3.5时,采用T-line-arc为开缝方案;当叶尖速比λ<3.5 时,采用T-line 为开缝方案。以λ=2.0 为例分析显示,采用对称开缝翼型,叶片失速区范围下降61.5%。3 翼缝形状对翼型气动性能的影响
3.1 弧形半径

3.2 不同组合形式翼缝

4 结果与讨论
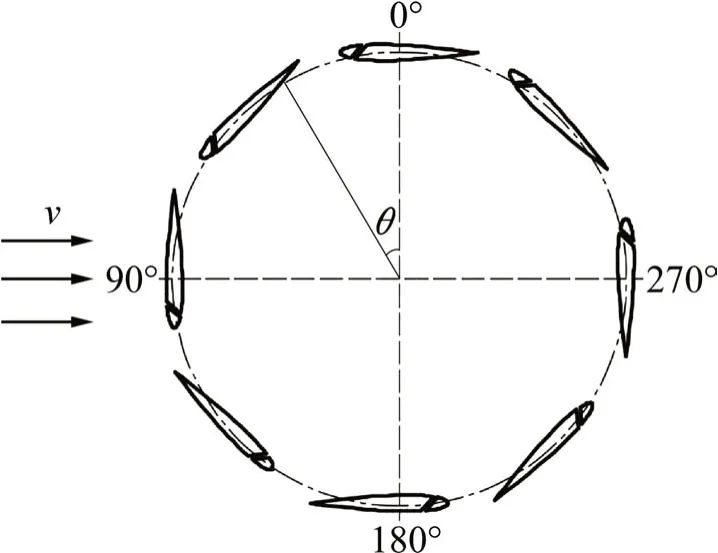
4.1 不同风区翼型开缝机理分析


4.2 对称开缝翼型效果分析
5 结论
