基于逆向拟合法的H13钢J-C本构修正模型
2019-09-18张静张松李斌训
张静,张松,李斌训
(1.山东大学机械工程学院,高效洁净机械制造教育部重点实验室,山东济南,250061;2.山东大学机械工程国家级实验教学示范中心,山东济南,250061)
近年来,随着对切削机理及数值模拟研究的不断深入,材料的流变应力行为建模受到了广泛的关注。其中,材料塑性变形的流变应力是预测切削变形力学行为和微观组织性能以及制定切削加工工艺的重要依据之一[1]。因此,准确建立材料在高温、高应变率条件下的本构方程,对研究材料的高速切削加工性能以及切削层材料损伤具有重要意义。在工程材料动态力学行为研究中,通常利用分离式霍普金森压杆实验来建立材料的本构关系方程。针对不同的材料参数的求解,传统的方法是对实验获得的应力和应变反复进行运算处理,然后逐个求出相应的模型参数。陈刚等[2-5]提出了一种基于数字图像相关(digital image correlation,DIC)技术逆向建立材料本构方程的方法。鲁世红等[6]利用霍普金森压杆实验,研究了H13钢的高应变速率动态性能,并建立了该材料在温度为293~873 K,应变率为103~104 s-1条件下的J-C 本构模型。ZHANG 等[7]利用DIC 技术获得加工过程中的切削力以及工件变形区域,再结合有限元仿真确定了Al6061-T4 在切削状态下的本构方程。李涛等[8]利用有限元仿真建立了淬硬模具钢正交切削的力学模型,并构建了模具钢在温度为273~873 K,应变率为700~6 000 s-1条件下的J-C本构方程。在上述本构模型中,材料参数被视为常数,这些本构模型往往仅适用于预测特定条件下的材料流变应力行为,当实验条件超过特定范围的应变温度或者应变率时,预测精度往往较低。造成上述问题的主要原因是没有考虑本构模型中的温度、应变率和应变对材料高温流变行为的影响及耦合作用。针对上述问题,BOBBILI等[9]建立了高熵合金FeCoNiCr 在温度为298~873 K 和应变率为0.01~3 500 s-1条件下的修正型J-C 本构模型,提高了对该材料流变应力行为预测的准确性。ASHTIANI等[10]建立了基于应变补偿型AA2030铝合金的本构模型,可以准确预测该材料在温度为623~773 K 和应变率为0.005~0.500 s-1条件下的流变应力。LIN 等[11]建立了基于应变率补偿型Al-Zn-Mg-Cu合金的本构模型,在温度为573~723 K 和应变率为0.001~0.100 s-1条件下对预测该材料的流变应力具有较高的准确性。SONG等[12]提出了一种针对钛基复合材料修正型J-C本构模型,以预测该材料在温度为293~923 K 和应变率为0.001~1 252.000 s-1条件下的动态特性。LIN等[13]考虑了温度对材料流变应力的影响,建立了基于温度补偿型7075 铝合金的本构模型,该修正模型在温度为350~450 ℃和应变率为0.001~0.100 s-1的条件下表现出了较好的预测性能。然而,修正型本构模型在构建过程中往往涉及到大量数据的处理与运算,并且在数据处理过程中,数据的选取对计算结果会产生很大的影响。其次,大多修正型J-C本构模型只建立了材料参数关于温度、应变率或者应变单个因素的函数,并未考虑多个因素耦合的影响。因此,用这些修正模型去预测不同条件下的材料流变应力时,仍然存在较大的误差。H13钢是一种常用的热作模具钢,具有优良的使用特性。该钢在较高温度时具有较高的强度和硬度,较高的耐磨性和韧性,优良的综合力学性能和较高的抗回火稳定性,因此在现代模具制造业中得到了广泛的应用。为了更准确地建立H13 钢在高温(298~1 073 K)和高应变率(1 ~15 000 s-1)条件下的J-C 本构模型,本文作者提出一种基于自定义函数来确定本构模型参数的逆向拟合法,并对材料参数进行修正,以期简化J-C本构模型的建立过程,消除传统求解方法中的多次拟合误差,进一步提高对材料流变应力预测的精度。
1 H13钢力学性能实验
1.1 实验材料
实验所用的材料为H13 钢(相当于国内牌号4Cr5MoSiV1),材料化学成分如表1所示。
利用光学显微镜(OM)和透射电镜(TEM)对H13钢的微观组织进行观察,不同实验设备下H13钢微观组织如图1所示。由图1(a)可知:材料初始晶粒粒径均匀,利用Imagine-Pro-Plus(IPP)软件进行统计分析发现晶粒直径约为23.85 μm。由图1(b)可知:板条状马氏体在材料组织中均匀分布,对应的衍射光斑呈点阵排列,无圆环显示,说明材料原始晶粒直径较大。
1.2 准静态实验
在温度T为298 K(25 ℃),应变率为1 s-1的条件下,利用万能式电子试验机获得了H13钢的准静态应力和应变曲线,如图2所示。由图2可知:H13 钢在准静态条件下没有明显的屈服现象,根据仪器测试结果可得材料的屈服强度σ0=1 605 MPa。
1.3 霍普金森压杆实验
霍普金森压杆实验温度分别为473,623,773,923,1 073 K,应变率分别为5 000,10 000,15 000 s-1,共计15组实验。实验装置示意图如图3所示。当温度为623 K,应变率为5 000 s-1时试样压缩前、后的形状如图4所示。

表1 H13钢化学成分(质量分数)Table1 Chemical composition of H13 steel %

图1 H13钢微观组织图Fig.1 Microstructure of H13 steel

图2 准静态条件下H13钢的真应力-真应变曲线(T=298 K,=1 s-1)Fig.2 True stress-true strain curve of H13steel under quasistatic condition(T=298 K,=1 s-1)

图3 高温Hopkinson压杆装置示意图Fig.3 Schematic map of Hopkinson device at high temperature

图4 实验试样(T=623 K,=5 000 s-1)Fig.4 Experimental specimen(T=623 K,=5 000 s-1)
由于实验材料H13 钢的屈服强度较高、硬度较大,因此,通过选用不同长度的子弹来实现不同的应变率。当应变率分别为5 000,10 000,15 000 s-1时,对应的子弹长度分别为12.5,7.0 和5.0 cm。为了达到较高应变率,当应变率分别为5 000 s-1和10 000 s-1时,采用试样直径×高为1.8 mm×2.0 mm;当应变率为15 000 s-1时,采用试样直径×高为1.8 mm×1.5 mm。考虑到实验过程中的误差和其他环境影响,每组实验重复多次,取3次有效值。
图5所示为H13钢在不同应变率和温度条件下的真应力-真应变曲线。从图5可以看出:当温度一定时,随着应变率的提高,材料的真应力不断增大。单位时间内应变率越大,材料塑性变形越严重,严重的塑性变形导致了高的位错密度,从而阻碍了材料内部晶粒发生滑移变形,使得变形抗力不断增大。同样,当应变率一定时,随着温度的升高,材料的热软化效应逐渐明显。一方面,动态软化使得塑性变形过程中的位错密度降低,减小了材料的变形抗力。另一方面,高温将会推动材料发生动态再结晶,再结晶晶粒形核,降低位错密度,低的位错密度和较小的再结晶晶粒使得材料更容易发生滑移变形,继而减小材料的变形抗力。在高温、高应变率条件下,温度和应变率这2 种影响机制在材料的变形过程中同时发生,因此,在构建H13钢的J-C本构方程时,要考虑应变率和温度对材料流变应力的影响及其耦合作用。

图5 H13钢在不同应变率和温度下的真应力-真应变曲线Fig.5 True stress-true strain curve of H13steel under different strain rates and temperatures
2 J-C本构方程参数的确定
J-C本构模型形式简单、准确率高,且利用较少的实验数据就能得到所有材料参数,因此被广泛应用于材料流变行为的研究[14-15],其关系式如下:
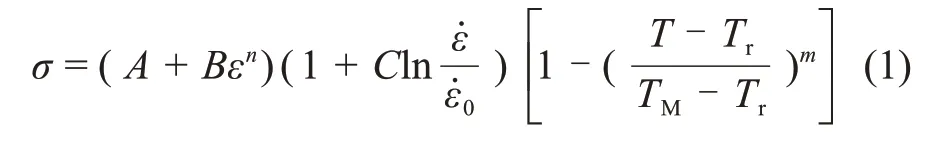
式中:σ为H13 钢的应力;A为参考条件下的屈服应力;B为应变硬化系数;n为应变硬化指数;C为应变率强化系数;m为温度软化系数;ε为应变;为参考应变率,=1 s-1;Tr为参考温度,Tr=298 K;TM为材料的熔点温度,对于H13钢,TM=1 773 K。
常见的H13 钢J-C 本构模型的材料参数见表2。由表2可确定材料参数取值范围为:B小于1 100 MPa;n小于0.65;C小于0.06;m小于3。
2.1 应变强化系数的确定
在温度T为298 K,应变率为1 s-1的参考条件下,可以忽略应变率强化以及热软化的影响,此时J-C本构方程可简化为准静态本构方程:

式中:A=1 605 MPa。首先在软件中绘制出参考条件下的真应力-真应变曲线,然后将式(2)嵌入到Origin函数库中,然后利用该软件中的自定义函数的拟合功能,从函数库中调用上述函数并设置函数的参数范围,最后,对该参考条件下的真应力-真应变曲线进行拟合,直至达到最优解,从而得到本构函数中的材料参数。根据B和n的取值范围以及拟合结果可得B=472.36 MPa,n=0.096 78。参考条件下自定义函数拟合曲线如图6所示。静态本构方程为

2.2 应变率强化系数和热软化系数的确定
在准静态条件下,通过自定义函数拟合确定H13钢的应变率强化系数,其J-C本构方程为
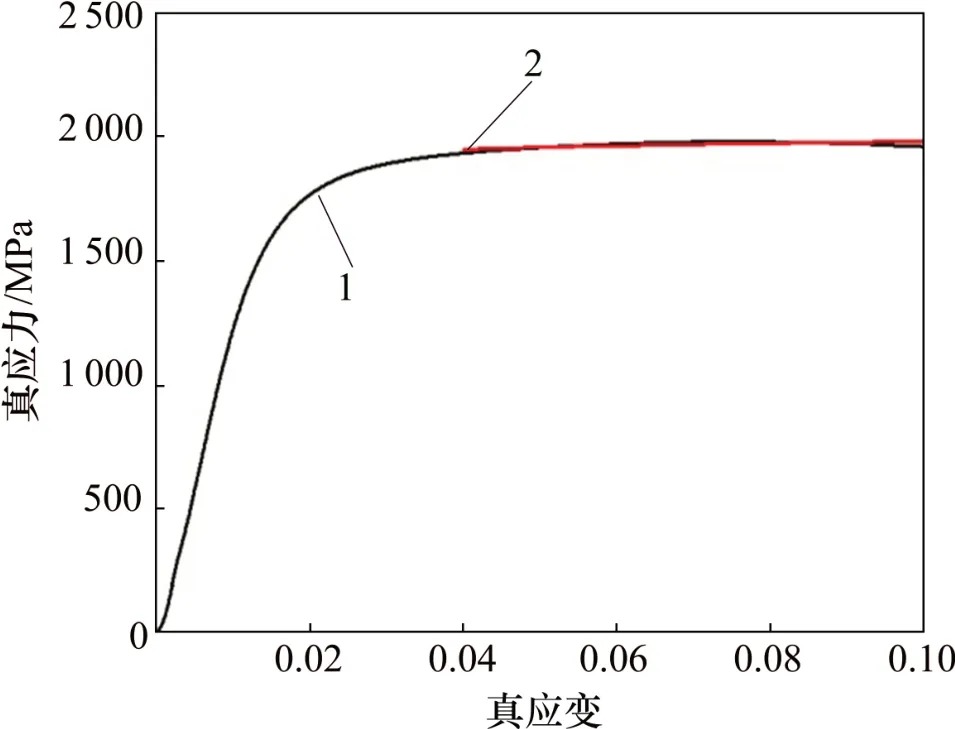
图6 参考条件下自定义函数拟合曲线(T=298 K,=1 s-1)Fig.6 Fitting curve of custom-function under reference condition(T=298 K,=1 s-1)

对于式(4)中C和m的确定,需要利用霍普金森压杆实验获得的真应力和真应变。首先,将式(4)嵌入到Origin 函数库,然后绘制应变温度分别为473,623,773,923 和1 073 K,应变率分别为5 000,10 000,15 000 s-1时的13 组真应力-真应变曲线,其中应变率和温度为15 000 s-1和773 K 以及10 000 s-1和923 K 这2 组作为后续模型验证。其次,利用Origin软件中的自定义函数拟合功能,从函数库中调用上述函数并设置函数参数范围,对以上真应力-真应变曲线分别进行拟合(参数范围见表2)。最后,得到13组不同条件下C和m的拟合值,分别如表3和表4所示。部分实验条件下C和m与温度和应变率的变化关系分别如图7和图8所示。
由图7和图8可知:应变率强化系数C和热软化系数m随温度和应变率的变化而变化,故该材料参数并非为恒定的常数。因此,考虑到应变率和温度对流变应力的耦合作用,令并分别对C和m进行二元多项式拟合,则有:

式中:ak1k2和bk1k2分别为多项式系数;k1和k2为非负整数。由拟合结果可得:


表2 H13钢J-C本构方程的材料参数Table2 Material parameter of J-C constitutive equation of H13 steel

表3 不同条件下参数C的拟合值Table3 Fitting value of parameter C under different conditions

表4 不同条件下参数m的拟合值Table4 Fitting value of parameter m under different conditions

图7 C与温度T和应变率之间的关系Fig.7 Relationship between C,T and

图8 m与温度T和应变率之间的关系Fig.8 Relationship between m,T and

即:

综合上述各材料参数可得H13 钢在温度为298~1 073 K,应变率为1~15 000 s-1条件下的J-C 本构方程如下:

2.3 模型验证
选取温度T=773 K和=15 000 s-1以及T=923 K和=10 000 s-1这2组工况下所得的真应力和真应变对修正的J-C本构模型进行验证,并计算其相对误差,预测结果如图9所示。由图9可知:真应力预测值和实验值较吻合,并且最大相对误差为3.9%,该修正型J-C本构模型能够真实反映H13钢塑性变形过程中的流变行为。因此,用该方法获得的修正型J-C本构模型,不但减少了大量的数据处理工作,而且提高了对材料流变应力预测的精度。

图9 不同条件下真应力实验值与预测值对比及其相对误差Fig.9 Comparison of experimental and predicted true stress and its relative error at different conditions
3 结论
1)通过准静态拉伸实验,利用逆向拟合法得到H13 钢静态本构方程σ- 1 605 = 472.36ε0.09678。在准静态条件下,该静态本构方程为动态流变方程的特殊形式。
2)真应力随着应变率的提高而不断增大,随变形温度的升高而降低;随着应变率的不断提高,应变率强化系数C和热软化系数m呈现不断增大的趋势;但随着变形温度的增大,二者先增大再减小,在773~923 K时达到最大值。
3)利用自定义函数逆向拟合法所建立的修正型J-C 本构模型可以精确预测H13 钢在温度为298~1 073 K 和应变率为1~15 000 s-1的条件下的流变应力;与以往建立材料本构模型的方法相比较,该方法减少了大量的数据处理与运算工作,简化了材料本构模型的建立过程,而且该修正模型综合考虑了温度与应变率对材料流变行为的耦合影响,可为工程分析提供参考。
