开发数学应用问题课程资源的实践探究

孔传辉

培养学生数学应用意识是数学教学核心目标之一，开发数学应用问题的课程资源有助于培养思维能力，增强学生对数学的理解和应用意识，从而实现数学价值，有效培养学生数学素养.但许多教师开发课程资源的意识比较淡薄，过分依赖教材“供给制”，使学习资源缺少灵活性.因此开发数学应用问题课程资源是数学教学十分有研究价值的课题.

一、巧用教材

1.紧扣变化，结合时代

教材虽然提供了较为丰富的常规应用题，但已满足不了学生需求，教师要与时俱进地对教材的常规应用题进行创新，以激发学生学习兴趣.改编时可赋予题目新时代背景下的文字气息、改变设问方式、变换题设条件、互换条件结论，或者拓展类比成新的数学建模应用问题.

【案例1】 甲乙两地相距250km，某天小颖从上午7：50由甲地开车前往乙地.在上午9：00、10：00、11：00这三个时刻，车上的导航仪都进行了相同的提示：如果按出發到现在的平均速度继续行驶，那么还有1个小时到达乙地.如果导航仪的提示语都是正确的，那么在上午11：00时，小颖距乙地还有       km.

【评析】本题是一道常见传统行程应用题，看似不起眼，但加入车和导航仪这个新时代背景下的文字，整个题就鲜活起来，契合时代特点，一下子就把学生的兴趣调动起来，这是一种很好的对数学常规应用题进行加工再创造的方法.

2.顺应背景，契合实际

纯数学问题需要创造相应的背景，放在实际的环境中去解决，按照科学性、现实性、新颖性、趣味性和可行性的原则，创设学生熟知的生活背景，根据实际情况设计有一定应用价值的应用问题，有助于丰富和延伸纯数学问题的内涵和应用价值.

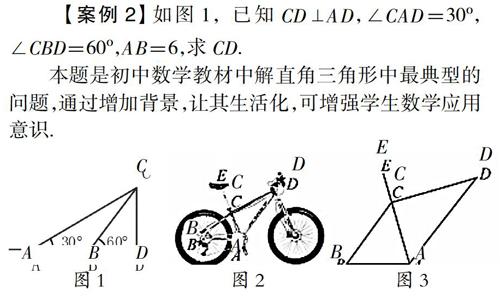
【案例2】 如图1，已知CD⊥AD，∠CAD=30？紫，∠CBD=60？紫，AB=6，求CD.

本题是初中数学教材中解直角三角形中最典型的问题，通过增加背景，让其生活化，可增强学生数学应用意识.

背景：学校倡导“低碳生活”，鼓励学生以自行车作为代步工具.如图2所示是学生小沈的自行车的实物图.车架档AC与CD的长分别为45cm，60cm，且它们互相垂直，座杆CE的长为20cm，点A，C，E在同一条直线上，且∠CAB=60？紫，如图3.

（1）求车架档AD的长;

（2）求车座点E到车架档AB的距离.

【评析】本题引入了环保热点问题，情境设置自然，贴近学生的生活，设计有现实性、趣味性、话题性，不仅能使学生感受到数学学习乐趣，并且能让学生关注生活中的数学问题，体会数学的应用价值.

二、借助环境

1.校园为本

教师要关注校园生活，善于发现校园中的数学资源，为开发应用问题作资源支撑.例如：上课时间与注意力最佳问题、长跑时心率与极限问题、投掷实心球角度问题、校园内不爬高测旗杆高问题、教室采光问题，等等.

【案例3】 学校即将开运动会，但是学校跳远场地的沙坑前段时间被雨水冲出了一个“圆锥形坑”.数学老师要求数学课外活动小组的同学去解决沙坑的填埋问题，同学们于是带着皮尺去测量这个“圆锥形坑”的深度，图4所示是同学们选择测量方案：

①先测出沙坑坑沿的圆周长是10.54m;

②甲同学直立于沙坑坑沿的圆周所在的平面上，经过适当调整自己所处的位置，当位于B时恰好视线经过沙坑坑沿圆周上一点A看到坑底S（甲同学的视线起点C与点A，S三点共线），经测量：AB=1.2m，BC=1.6m.

根据以上测量数据，求“圆锥形坑”的深度（圆锥的高）.

【解析】取圆锥底面圆心O，连结OS，OA，

则∠O=∠ABC=90？紫，OS∥BC，

∴∠ACB=∠ASO，

∴△SOA∽△CBA，

∴=，∴OS=

∵OA=≈1.68，BC=1.6，AB=1.2，

∴OS≈2.3，

∴“圆锥形坑”的深度约为2.3m.

【评析】此题是关注校园生活，提炼数学资源，解决实际问题的典例.这样的设计形式搭建了生活资源的载体，有助于引导学生充分提炼学习资源，丰富学习内容和方式.

2.探寻家庭

生活中处处充满着数学，家庭生活是学习数学的起源，教师要引导学生以观察、调查、实践等形式主动收集应用数学的信息，捕捉家庭生活中的数学问题或数学现象，开发自主学习能力.

【案例4】在十一黄金周期间，小王和爸爸妈妈去安吉大峡谷漂流，在售票大厅看到表（一）和表（二），小明思考了一下，对爸爸说：“若漂流船在静水中的速度不变，那么我能算出它的速度和水流速度.”爸爸说：“你真聪明！”你知道小明是如何求出的吗？请你试着求漂流船在静水中的速度和水流速度.

【评析】这道题通过对现实生活中的事件进行“素材”编拟，呈现的信息是开放的，但并非所有信息都是有效，需要进行合理的取舍，这类问题能激发学生解决问题的内在动力，获得真实的内心体验，感受数学无处不在.

三、综合拓展

1.有效改编

经典试题一直是数学应用的资源平台，许多中考试题、pisa测试题都可以用来作为开发数学应用问题课程的素材.Pisa类测试可强化对学生知识面、综合分析、创新素养等方面的培养，教师在教学中要充分利用这些素材提高学生的数学能力.

【案例5】已知A地在B地的西方，且有一以A、B两地为端点的东西向直线道路，其全长为400公里.今在此道路上距离A地12公里处设置第一个广告牌，之后每往东27公里就设置一个广告牌，如图5所示.若某车从此道路上距离A地19公里处出发，往东直行320公里后才停止，则此车在停止前经过的最后一个广告牌距离A地多少公里？（   ）

A.309     B.316     C.336      D.339

【解析】設此车停止时前面有x个广告牌，根据题意得12+27（x-1）≤320+19，x≤13，即此车停止时前面有13个广告牌，并且超过第13个广告牌3公里，所以此车在停止前经过的最后一个广告牌距离A地320+19-3=336公里.故选C.

【评析】这道经典习题背景直观、学生熟悉，通过改编设计，帮助学生利用不等式的数学模型，进行可行性研究，让学生感受到数学模型的重要性，提高学生的建模能力.

2.学科整合

数学与其他学科之间有较多联系，教师要试着以不同的学科知识为背景，或以相关学科知识为载体来设计问题，充分体现数学与其他学科间的整合，让学生从不同的方向和角度感受数学知识的产生与变化、发展与应用的过程，拓展学科知识视野，提高综合能力.

【案例6】桌面上有甲、乙、丙三个圆柱形的杯子，杯深均为15公分，各装有10公分高的水，且表（三）记录了甲、乙、丙三个杯子的底面积.今小明将甲、乙两杯内一些水倒入丙杯，过程中水没溢出，使得甲、乙、丙三杯内水的高度比变为3∶4∶5.若不计杯子厚度，则甲杯内水的高度变为         公分.

A.5.4      B.5.7      C.7.2      D.7.5

【评析】这一问题融合了数学中的比、方程思想、科学实验与体积变化等知识，使学生充分利用学科知识之间的联系来解决实际问题.学科的有效整合、综合运用让学生找到应用数学的广阔途径，从而呈现数学的丰富内涵，突出了数学作为工具学科的本质.

总之，教师在数学教学中要针对不同层次学生因材施教，开发不同层次的数学应用问题，遵循“科学性、客观性、适切性、时代性、探索性、开放性、动态性”等原则，处理好“生活化”与“数学化”的关系，多渠道、多角度、全方位拓宽数学应用问题的课程资源，较好地提升学生数学素养.