因为差异,教师的提问方式需要“转型”
2019-09-17罗仲民
罗仲民
摘 要:随着我国基础教育课程改革逐渐走向深入,教师的课堂提问行为已成为课堂教学的重要一环,并且越来越受到教师的普遍关注。课堂提问的主体是教师,改革课堂提问方式的主体也是教师;教师在自己的课堂教学中,往往要面对各种存在差异的学生,在陈述问题时,应该机智灵活地调整自己的提问方式,适时“转型”,激励引导不同层次的学生进行学习与思考,突破“最近发展区”,从而有利于教学目标的实现。
关键词:学生的差异;教师提问;“转型”
本文着重从学生的智力差异、认知差异、能力差异、思维差异等角度,来阐述教师的提问方式需要“转型”的类型。
一、从学生知识能力差异方面来说,教师的提问需要“转型”的类型
1.并列式
课堂上这类形式问题的提出,具有普遍性,适用的对象是各种层次的学生,它针对的面广,特别适合“双基”问题的提出;也是不同层次的学生大多都能掌握的知识问题。
【片段一】:2、5的倍数的特征。
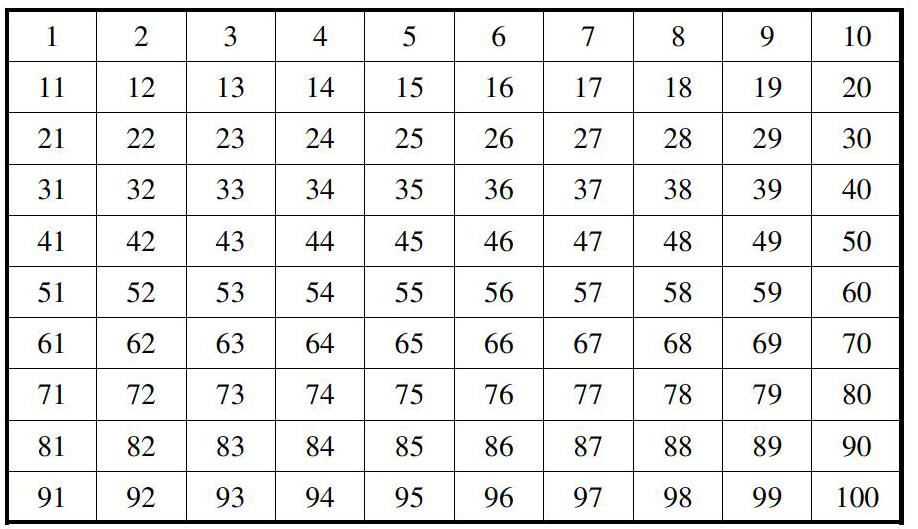
教师先复习因数、倍数的概念;让学生说出怎样求一个数的因数和倍数的方法后,然后首先出示一张100以内的整数表:
师:上表中哪些是2的倍数?哪些是5的倍数?把它们用不同颜色的笔圈起来,你发现了什么?
生1:上面这个表格中是2的倍数有:2、4、6、8、10、12…100
生2:是5的倍数有:5、10、15、20、25、30、35、40…100
师:很好,请同学们继续观察:2和5的倍数分别有什么特征?你有什么发现?
生3:2的倍数的特征:个位上是0、2、4、6、8的数都是2的倍数的特征。
生4:5的倍数的特征:个位上是0或5的数都是5的倍数的特征。
上述片段教师提出的问题,就是两个并列式问题,它们都是平行性问题,没有什么主次之分,这些问题都是在学生掌握了倍数和因数的两个概念后,教师有意让一些中下生优先回答这些问题,然后由点到面,可以推测到其他层次的学生也都能够把这两个不同的知识点掌握了。
2.递进式
由于学生的智力发展水平及个性特征的不同,学生对同一问题理解的广度和深度必然存在着明显的差异;智力好的学生,能够对问题所关注的内容有深刻的理解,包括问题中的事实、数据和相关的概念、知识等;智力不好的学生,则刚好相反;长期这样,会导致学生的发展性差异。面对深层次的问题,有些学生感到迷惑、受困,无从下手,这就要求教师在提问时,需要进行“转型”,不要把解决问题的方式玩得很高,让大多数学生感到教师解决完这个问题后,还是感到很茫然,一头雾水。对于高水平的问题,教师必须要用高质量的提问方式把呈现的问题进行肢解,转化为一个个小问题,然后一步一步地对学生加以启发、引导,使问题层层推进,激发学生的学习热情和学习兴趣,直到目标问题得到解决。
【片段二】:五年级上册第110页《植树问题》中有一道这样的练习题:
一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……,照这样,10张桌子并成一排可以坐多少人?
有些学生一见到这个要求的数学问题,就感到很茫然,一脸疑惑,这怎么与植树问题扯到一块,脑子总是跳不出这个思维。其实,教师在课堂上只要采取递进式的提问方式,就能找出其中的规律:
师:题目中已经知道了一张桌子坐几人?
生:6人。
师:两张桌子坐几人?怎么坐的?
生:10人一张桌子坐6人,分开的两张桌子可以坐12人,如果两张桌子并在一起接头处不能坐人,所以只能坐10人。
师:三张桌子坐几人?
生:14人。
师:四张桌子呢?
生:18人。
……
师:现在我把这些数写在黑板上,请同学们找一下规律:
6、10、14、18…
生:老师,我发现了:以后每并一张桌子都只能增加4人,如果有n张,我们就可以用含有字母的式子表示结果:6+4×(n-1)人,照这样,10张桌子可以坐:把n=10代入,算出共42人。
师:同学们都非常棒!
根据维果斯基的最近发展区理论,一开始,同一问题,对于不同层次的学生,往往得到因人而异的反馈;紧接着,教师通过层层递进提问引导,使学生一步一步朝着即将达到的知识水平方向发展。好的、有效的提问是促进学生学习的燃料。
二、从外部因素或内部自身因素发生的变化来看,教师的提问需要“转型”的类型
1.因果式
有的是由外部因素问题引起的提问;有的是由事物内部自身的因素引起的有关变量发生改变的提问。
【片段三】:人教版五年级上册《平行四边形的面积》中的练习环节教学:
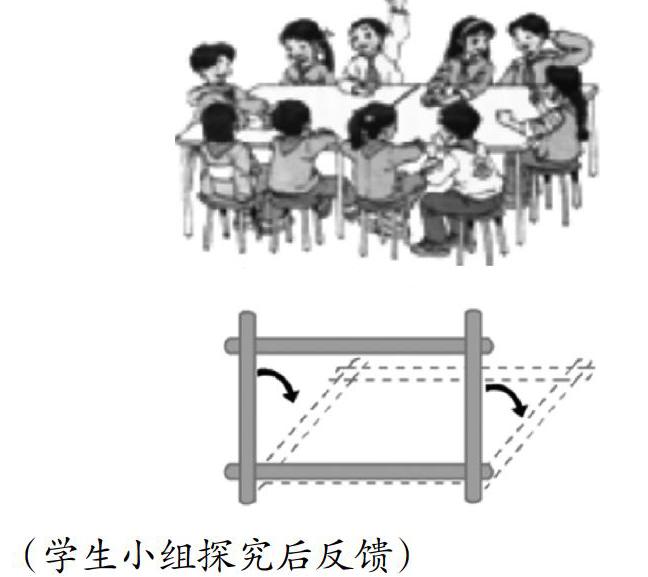
师:小组合作探究:把一个用木条做成的长方形框架(如下图),长22cm,宽17cm,把它拉成一个平行四边形,周长和面积有什么变化?为什么?
生1:我们组通过把做成的长方形木条拉成一个平行四边形后,发现它的周长没有变化;原因是虽然形状变了,但四条边的长度没有变化,所以周长不变。
生2:我们组通过把做成的长方形木条拉成一个平行四边形后,发现它的面积发生变化,并且变小了;原因是形状变了,平行四边形的高变短了,而底边不变,所以面积也变小了。
上述的片段是一个实践操作性的探究问题,学生借助学具一边操作,一边带着教师的提问进行探究,通过观察、分析发现:周长没有因形状的改变而发生变化,面积因形状的变化导致平行四边形的高发生改变;这种因果式的提问方式,既培養了学生在动态中寻找变化的主因在哪里,又培养了学生的分析推理能力,关注了学生的思考过程,师生在互动过程中获得“鲜活”的反馈。
