有效提升小学生数学解决问题能力的教学对策初探

洪振华

《义务教育数学课程标准（2011年版）》中提出“初步学会从数学的角度发现和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力。获得分析和解决问题的一些基本方法，体验解题方法的多样性，发展创新意识”。可见，在解决问题的教学中，教师要让学生经历数学思考的过程，积累发现问题、提出问题、解决问题的经验，培养学生问题解决的能力，促进学生形成应用意识、推理能力、创新意识以及良好的思维习惯和能力是十分必要的。

多年小学高年级数学教学实践，笔者发现不少学生在数学学习中，相比较于计算、概念、几何图形等学习内容，感觉最困难的是解决问题，会出现诸如此类的现状：看到题目不知从何下手;只会依葫芦画瓢，仿照例题解题;解决了问题得出了结果，却说不清算理……

一、问题的缘起

（一）设计问卷，了解学情

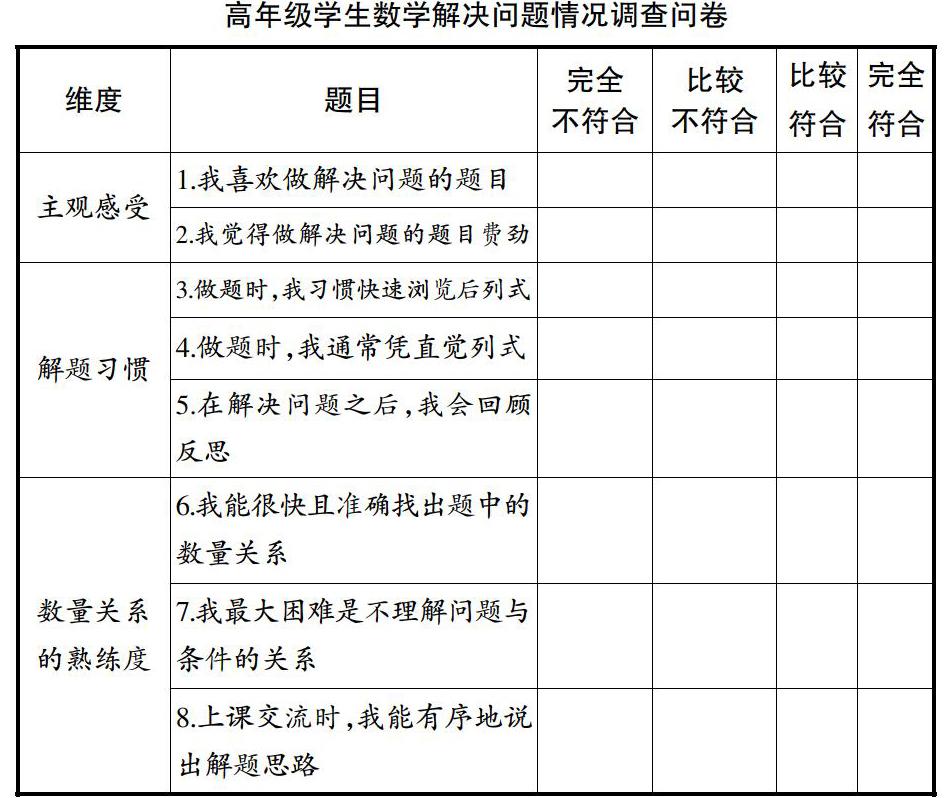
为了寻找高年级学生解决问题感觉困难的原因，笔者设计了一份问卷，从“主观感受”“解题习惯”“数量关系的熟练度”三个维度共8个子项了解学情。见下表：

（二）分析问卷，寻找成因

1.数据呈现的客观现状

发出、收回调查问卷75份，对收集的信息整理后，发现如下情况：

（1）学生不大喜欢做解决问题的题目，觉得相对比较费劲。从“主观感受”的选项看，第1题“我喜欢做解决问题的题目”选“完全不符合或比较不符合”占60%。第2题“我觉得做解决问题的题目费劲”选“比较符合”占33.3%，“完全符合”占8%。

（2）学生缺乏认真审题和反思检查的良好习惯。从“解题习惯”的选项看，第3题“做题时，我习惯快速浏览后列式”选“完全符合或比较符合”占53.3%;第4题“做题时，我通常凭直觉列式”选“完全符合或比较符合”占48%。第5题“在解决问题之后，我会回顾反思”选“完全符合或比較符合”占28%。

（3）学生分析数量关系的能力较差。从“数量关系的熟练度”的选项看，第6题“我能很快且准确找出题中的数量关系”只有34.7%的选“完全符合或比较符合”;第7题“我最大困难是不理解问题与条件的关系”选“完全符合或比较符合”占45.3%。第8题“上课交流时，我能有序地说出解题思路”选“完全符合或比较符合”只有25.3%。

2.反思主要原因

一是忽视以题论理。知识有形，而题型无限。而课堂教学常常出现“以题论题”，没有做到“以题论理”，引导学生“理出思路、方法”。一旦面对不同的题型时，学生就会出现“凭感觉，猜算法”的现象。

二是忽视分析数量关系。中低年级解决问题的数量关系相对简单，学生看题目凭经验比较容易就能列出算式。教师会有所大意，以为学生懂了，教学的重点发生偏移，数量关系分析不到位甚至缺位。

三是对良好学习习惯的重要性认识不足。学生对解题三部曲“阅读理解、分析解答、回顾反思”的好习惯未有足够的重视，对老师的要求只是应付了事，认真审题、回顾与反思的意识普遍淡薄。

二、提升的对策

（一）建立模式，熟悉常见的基本数量关系

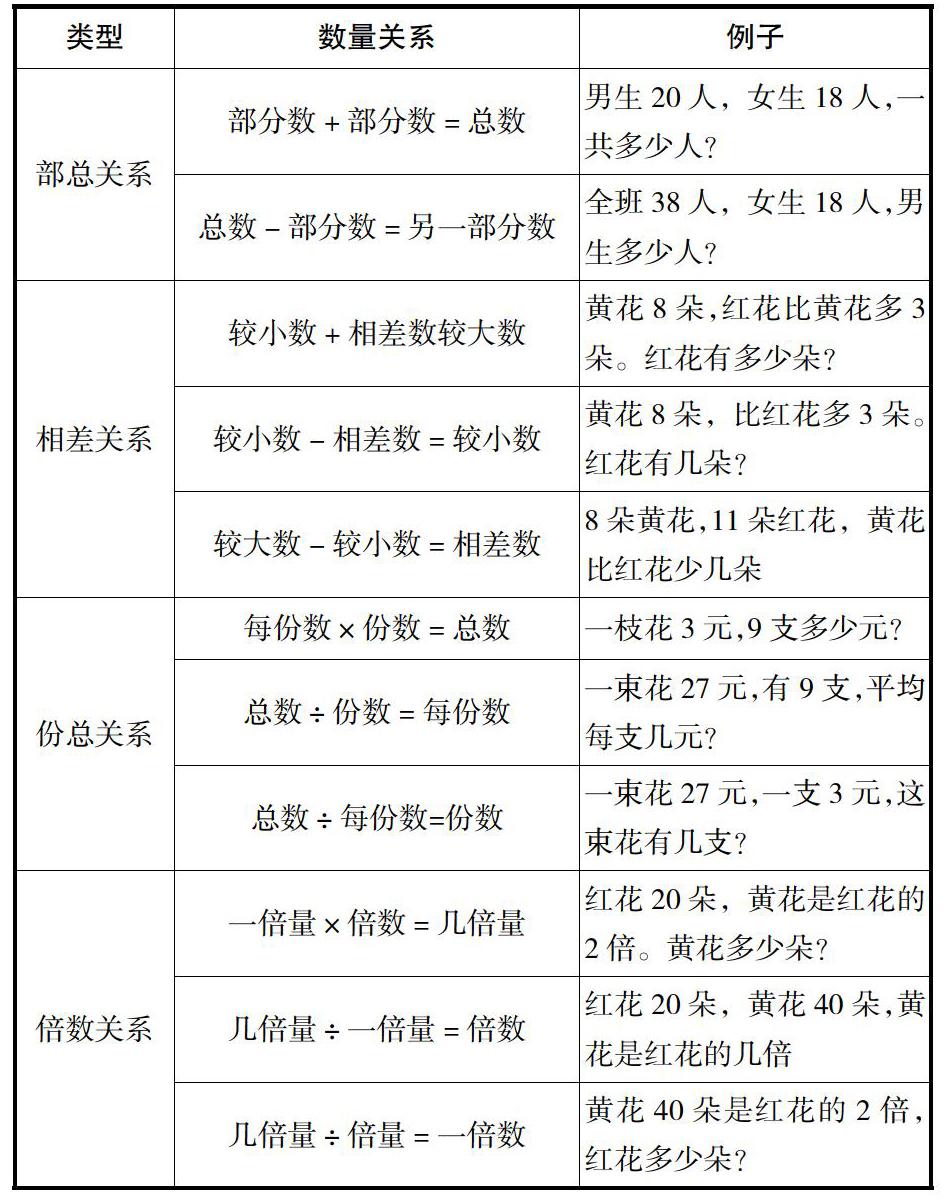
每道简单解决问题里都存在一定联系的三个数量，让学生熟悉数量之间的基本关系，学会分析数量间的联系，是正确解决实际问题的先决条件。在小学数学解决问题中的基本数量关系一共有四大类，见下表。

（二）启发联想，将数量关系融会贯通

1.根据条件联想问题。如：小红买了6支笔，小明买了2支。可以联想：①一共买了多少支笔？用“小红买的支数+小明买的支数=一共买的支数”;②小红比小明多买了多少支？或小明比小红少买了多少支？用“小红买的支数-小明买的支数=小红比小明多买的支数”;③小红买的支数是小明的几倍？用“小红买的支数÷小明买的支数=倍数”;④小明买的支数是小红的几分之几？用“小明买的支数÷小红买的支数=几分之几”。

2.根据问题联想出与相关联的两个条件。如“两天一共运化肥多少吨？”与它相关联的两个条件，可以是“平均每天运的吨数”和“运了2天”，用乘法：平均每天运的吨数×运的天数=一共运的吨数;也可以是“第一天运的吨数”和“第二天运的吨数”，用加法：第一天运的吨数+第二天运的吨数=一共运的吨数。

通过反复联想训练，学会依据关联的两个数量联想出问题，或者依据一个问题联想到另外两个数量，逐步熟练地掌握基本数量关系及三量之间的变化。

（三）叙述思路，掌握基本方法

古人云“言为心声，言乃说，心乃思。”就是说：语言反映思维，语言与思维密不可分。在教学中培养学生有条理、有根据地表达解题思路，有利于对数量关系的深刻理解和灵活运用。

例如：合唱队有女同学62人，是男同学人数的2倍，合唱队一共有多少人？教师要引导学生叙述思路：根据“合唱队有女同学62人，是男同学人数的2倍”，可以求出“男同学的人数”，用“女同学的人数÷2=男同学的人数”，再用“女同学的人数+男同学的人数=一共的人数”，可以求出“合唱队一共有多少人？”算式是62+62÷2。这样从条件出发分析、解决问题的方法就是“综合法”，即从实际问题的已知条件出发，根据数量之间的关系，先选择两个已知数量，提出所能解决的问题;再把求出的数量作为新的已知条件，与其他的已知条件搭配，继续提出所能解决的问题，这样由因导果，直至推出所要解决的问题为止。

相反，也可以运用“分析法”从问题出发分析、解决问题，即是从所求问题出发，根据数量之间的关系，找出解决这个问题所需要的两个条件，再把其中未知的条件作为新的问题，继续找出解决这个新问题所需要的两个条件，这样执果索因，直至所需的条件全部找到为止。要求“合唱队一共有多少人？”用“女同学的人数+男同学的人数=一共的人数”，由于男同学的人数没有直接告诉我们，所以要先算，用“女同学的人数÷2=男同学的人数”，算式是62+62÷2。

让学生经历一系列口头语言表达的演绎推理活动，加强了问题—条件—算式之间的联系，既加深了解数量之间的关系，又促进学生掌握分析、解决问题的基本方法，从而有效提高逻辑思维和解决问题的能力。

（四）分析比较，正确推进理答

1.从运算的意义上分析比较

解决问题是以四则运算为载体，因此分析数量之间的关系必须以四则运算的意义作为思维的基础。如：

（1）同学做游戏，一组5人，另一组6人，一共有多少人？

（2）同学做游戏，分成5组，每组6人，一共有多少人？

通过比较，看清这两题叙述的事情和要求的问题都相同，但由于条件不同，所以解法也不同。第1题是把两个数合并起来，用加法。第2题是求5个6相加是多少，用乘法。如果用加法列式，就要5个6连加。经过这样分析，学生明白：这两道题都是求总数，加法中的加数可以相同，也可以不同;而乘法解决问题是求相同加数的和。

2.从概念的理解上分析比较

有些概念，虽然只有一字之差，可含义大相径庭，如不加以区别，很容易出错。教学中，要经常将一些易混淆的概念设计成题组进行比较，仔细鉴别，弄清概念，明确数量关系。如：

3.從事理的叙述上分析比较

题目中所叙述事情的道理即为事理。如二年级教学“求比一个数多（或少）几的数”，由于教材中的例题和开始练习的习题都是顺叙的。部分学生造成了见多就用加法、见少就用减法计算的思维定式，结果当出现逆叙的题目时，就造成意识泛化，出现负迁移，即使到了高年级也不例外。因此要经常将这类顺叙与逆叙的题目放在一起，进行对比分析，弄清题目里叙述的是谁跟谁比，谁多谁少，问题求的是什么数。

4.从结构的异同上分析比较

有些需要两步计算的解决问题，给出的条件和要求的问题跟一步计算的解决问题极为相似，学生很容易将两步计算的题目当作一步计算来解答。如：

（1）第一筐苹果50千克，比第二筐多5千克，第二筐有多少千克？

（2）第一筐苹果50千克，第二筐45千克，两筐一共多少千克？

（3）第一筐苹果50千克，比第二筐多5千克，两筐一共多少千克？

这三题都有两个条件和一个问题。但前两题是一步计算的，后一题是两步计算的。第（1）（3）题的条件完全相同，只是问题不同，第（2）（3）题的一个条件和问题完全相同，只是另一个条件不同，虽然解题的数量关系相同，都是用“第一筐的千克数+第二筐的千克数=一共的千克数”，由于第（3）题“第二筐的千克数”没有直接给告知，所以要用两步计算。通过分析比较，让学生明白：凡一步计算的题目，给出的两个条件都是直接知道的，而两步计算的题目，解决问题所需要的两个条件，其中的一个条件必定是间接的。另外，两道连续性的一步计算解决问题可以合并成一道两步计算解决问题，反之每一道两步计算解决问题必定能分成两道一步计算解决问题。在分析比较的过程中，学生认识和掌握两步解决问题的结构，学生能从问题出发，认真分析已知条件中的直接与间接的关系，提高学生的分析、综合能力。

（五）回顾反思，培养检查习惯

《义务教育数学课程标准（2011年版）》十分强调“评价与反思”，通过“评价与反思”的环节，去关注问题解决的过程，总结问题解决的方法。如此能锻炼学生挖掘和抓住事物本质的能力，培养学生“优化”的思想。从数学学习心理学的角度看，“评价与反思”本质上是一种元认知能力，它体现的是对自我思维的一种监控和调整，这在问题解决中尤其重要。教学中，首先要引导学生确立反思意识，明确检验的必要性;其次要教给学生一些具体检验的方法，如代入法、变换思路法、估算法、反证法等，教学中逐步渗透，以提高自我反思能力。

总之，提高学生解决问题的能力并非一朝一夕所能达成的，需要长期的、规范的、有意识的培养和训练。