单层金属卤化物CoX2(X=Cl、Br、I)可调能隙和磁性研究
2019-09-17陈红霞
陈红霞
(盐城师范学院新能源与电子工程学院,盐城 224007)
1 引 言
石墨烯的成功制备打开了二维材料之门,使人们得以在二维尺度空间研究材料的特殊性能[1, 2]. 由于二维材料具有诸多令人瞩目的物理、化学性质,使其成为目前国际材料科学研究的前沿焦点[3-9]. 科学家经过不断探索,发现了越来越多的二维材料,如氮化硼、二硫化钼、硅烯和锗烯等. 为了探索二维材料在自旋电子学器件方面的应用,人们考虑了缺陷、应变、吸附、掺杂等方法,尽管取得了一定的进展,但还有很多难题有待解决[10, 11].
尽管过渡金属卤化物体材料的层状结构稳定存在了很久,关于二维层状过渡金属卤化物的研究目前还相对较少. Zhang等人研究了单层CrX3(X=Cl、Br、I)材料,发现他们是稳定的铁磁性材料[12]. He等人研究了单层VX3(X=Cl、I)材料,发现他们具有内在的铁磁性和半金属性[13]. Zhou等人研究了TiCl3和VCl3材料,发现它们也存在半金属性[14]. Ashton等人研究了单层FeX2(X=Cl、Br、I)材料,发现它们具有半金属性[15]. 目前还没有关于单层CoX2(X=Cl、Br、I)材料的相关研究工作.
本文采用密度泛函理论系统地研究了单层CoX2(X=Cl、Br、I)材料的结构稳定性以及应变对材料物性的调节. 结果表明压缩应变不仅可以显著增强铁磁态的稳定性,还可以实现体系从间接带隙半导体向直接带隙半导体的转变.
2 理论方法和计算方案
单层CoX2(X=Cl、Br、I)材料是从相应的体材料结构中切割得到的. 为了避免相邻两层材料之间的相互作用,真空层厚度取为20 Å. 计算采用了基于密度泛函理论平面波赝势方法的CASTEP软件包. 交换关联势选择了GGA/PBE. 平面波截断能量取400 eV,总能的收敛标准为10-5eV/atom,力的收敛标准0.01 eV/Å,位置移动收敛标准为0.001 Å. 原胞和超原胞结构优化时,K点取值分别为8×8×1和4×4×1. 为了准确描述3d电子间的强相互作用,采用了GGA+U的方法. 经过测试,对三种材料中的Co原子,U取4.0 eV.
PBE/DND的准确性在前面关于ZnS体材料和纳米线掺杂磁性质研究工作中已经得到检验[16-19].
3 结果和讨论
3.1 晶体结构和稳定性
首先对单层CoX2(X=Cl、Br、I)材料进行了结构优化. 由于三种材料具有相似的结构,我们用CoCl2的结构图作为代表. 图1(a)和(b)画出了单层CoCl2材料优化后的顶视图和侧视图.
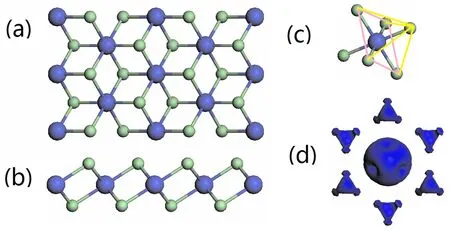
图1 单层CoCl2材料的顶视图(a)、侧视图(b)、八面体构型单元(c)和自旋电荷密度图(d). 大球代表Co原子,小球代表Cl原子. Figure 1 Top view (a), side view (b), octahedral configuration (c), and spin charge density (d) of monolayer CoCl2. Big ball, Co atom; small ball, Cl atom.
从图中可以看出,每个Co原子和六个Cl原子相连接;而每个Cl原子和周围三个Co原子相连. 这种结构是典型的八面体结构. 图1(c)画出了单层CoCl2材料中的八面体单元. 三种材料具体的结构参数列在表1中. 比较表1的数据可以发现,随着卤素原子半径的增大,晶格参数、Co-X键的键长都逐渐变大了;而Co-X-Co的键角却逐渐变小了.
为了考察三种单层材料的结构稳定性,我们计算了CoX2每个原胞的束缚能. 我们采用EB=-(ECoX2-ECo-2EX)来定义束缚能[20].ECoX2为单层过渡金属卤化物的总能量,ECo和EX为单个Co原子和单个X原子的能量. 计算结果也列在表1中. 三种单层材料的束缚能分别是9.01、8.04和6.95 eV. 这表明Co原子和卤素原子间存在很强的相互作用.
表1 单层CoX2的晶格参数(a)、Co-X键长(d, in A) 以及Co-X-Co键角(θ)、束缚能(EB)、Co原子的磁矩(μCo)、X原子的磁矩(μX)以及体系的总磁矩(μtot).
Table 1 The calculated lattice parameters (a, in Å), M-X bond lengths (d, in Å), Co-X-Co bond angles (θ, in degree), binding energies (EB, in eV), the magnetic moments (μCo, inB) of Co atom and the bonding X atoms (μX, inB) , and total magnetic moments (tot, inB) of monolayer MX2.
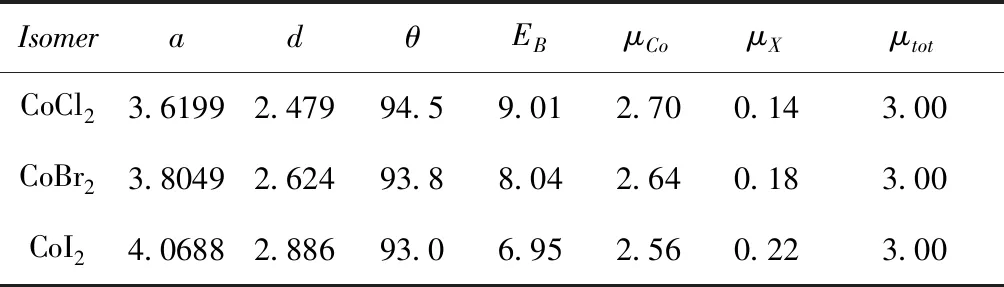
IsomeradθEBμCoμXμtotCoCl23.61992.47994.59.012.700.143.00CoBr23.80492.62493.88.042.640.183.00CoI24.06882.88693.06.952.560.223.00
3.2 电子性质
接着计算了它们的能带结构. 因为GGA在描述半导体能带时不够准确. 为了得到准确的能带图,我们采用了GGA+U的方法. 为了选择合适的参数U. 我们首先测试了U的取值对能带的影响. 对于CoCl2,经过测试,发现当U≤3.7 eV时,体系是间接带隙半导体,价带顶都在点,而导带底在M点. 当U>3.8 eV时,价带顶还在点,而导带底移到了K、点之间. 对于CoBr2和CoI2,作为分界的U值分别为3.5 eV和2.6 eV. 所以我们统一选取U=4.0 eV.
图2画出了自旋向上和自旋向下的能带图. 三种二维单层材料带隙分别为2.630、1.986和1.236 eV. 这和半导体硫化物中观察到的趋势一致,即随着硫化物原子序数的增大,带隙逐渐减小[20]. 从图中可以明显看出价带顶在点,而导带底在K、点之间. 三种二维体系都是间接带隙半导体材料.
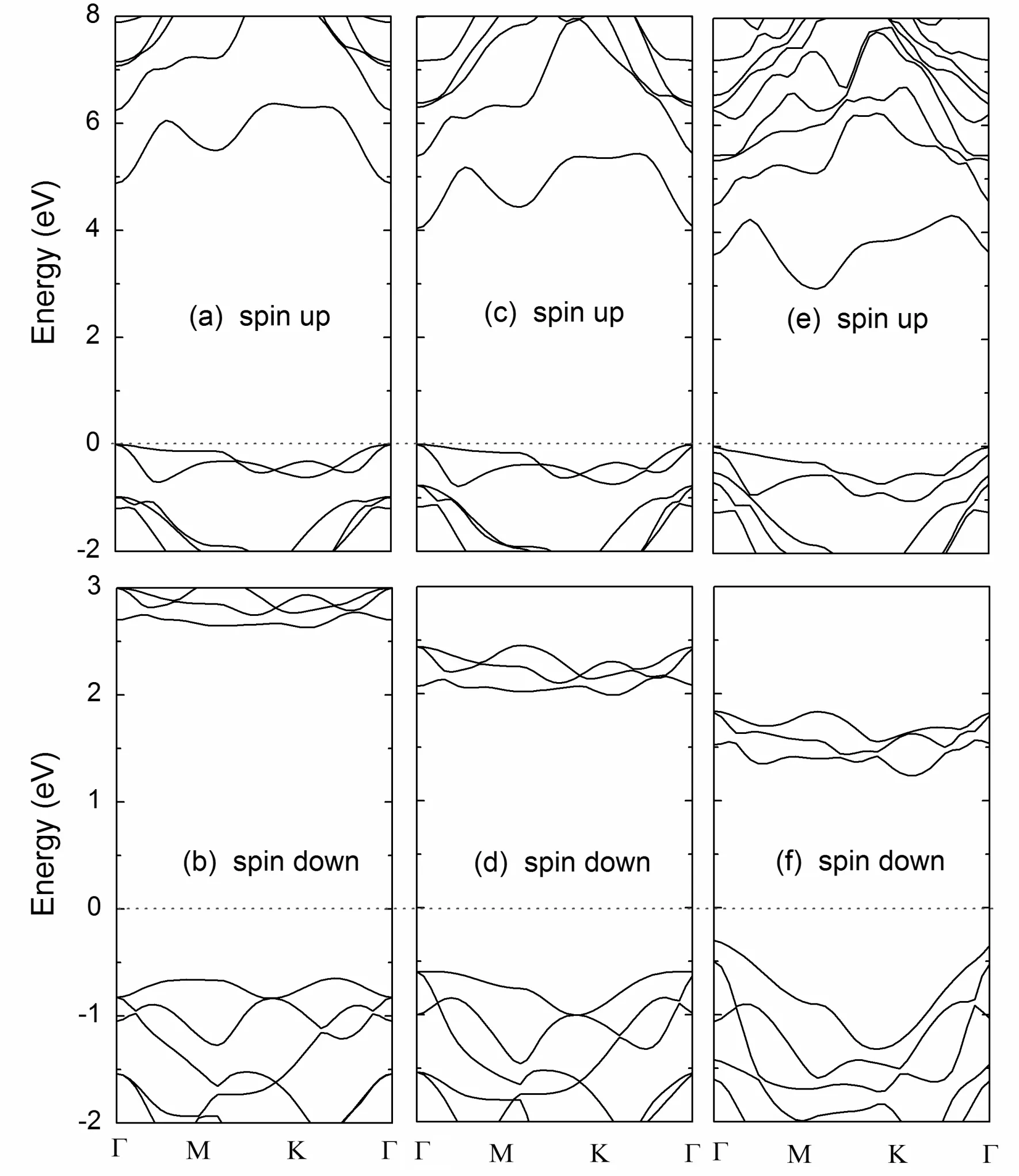
图2 CoCl2(a)、(b),CoBr2(c)、(d)、和CoI2(e)、(f)能带图. Figure 2 Band structures ofCoCl2, CoBr2, and CoI2.
3.3 磁性质
我们还计算了三种过渡金属卤化物的磁性质. 结果也列在表1中. 所有三种单层材料总磁矩都是3B. 因为在八面体晶体场中,d轨道被分为二重简并的和dx2-y2)能级和三重简并的t2g(dxy、dyz和dxz)能级. 在CoX2(X=Cl, Br, I)材料中,每个Co原子的构型是3d3,根据洪特定则,3个d电子正好排满三个自旋向上的能级,使得每个原胞的磁矩为3B. 原胞磁矩主要来源于Co原子的贡献. 由于杂化,相邻的卤素原子也贡献了很少量的磁矩. 而且它们的磁矩方向相同,表现出铁磁性. 我们还计算了自旋电荷密度. 我们同样采用CoCl2的结论作为代表. 图1(d)画出了CoCl2体系的自旋电荷密度. 从图上可以看出. 自旋电荷密度主要局域在Co原子,Cl原子上也有少量的自旋电荷密度.
为了研究磁性原子间的相互作用,我们建立了2×2×1的超原胞. 为了确定基态的磁性质,我们计算了铁磁态和反铁磁态的能量差E. 定义为ΔE=EAFM-EFM. 计算结果表明三种材料能量差分别为22.6、19.6和20.4 meV. 即三种材料都显示出铁磁态,但是铁磁性相对较弱.
如何增强材料的铁磁性呢?前人的研究表明,对二维材料施加双轴应变可以实现材料磁性的调节[21-23]. 为此,我们对三种材料施加了双轴应变. 双轴应变定义为η=(a-a0)/a0,其中a0和a分别表示无应变和加应变时超原胞的晶格常数.
图3(a)画出了三种卤化物单层材料铁磁态和反铁磁态的能量差随应变的变化图. 对于三种材料,压缩应变都增强了铁磁态的稳定性. 特别是CoCl2和CoBr2材料,应变对磁性的调节作用非常明显. 当η=-0.06时,体系铁磁态和反铁磁态的能量差达到46 meV左右.
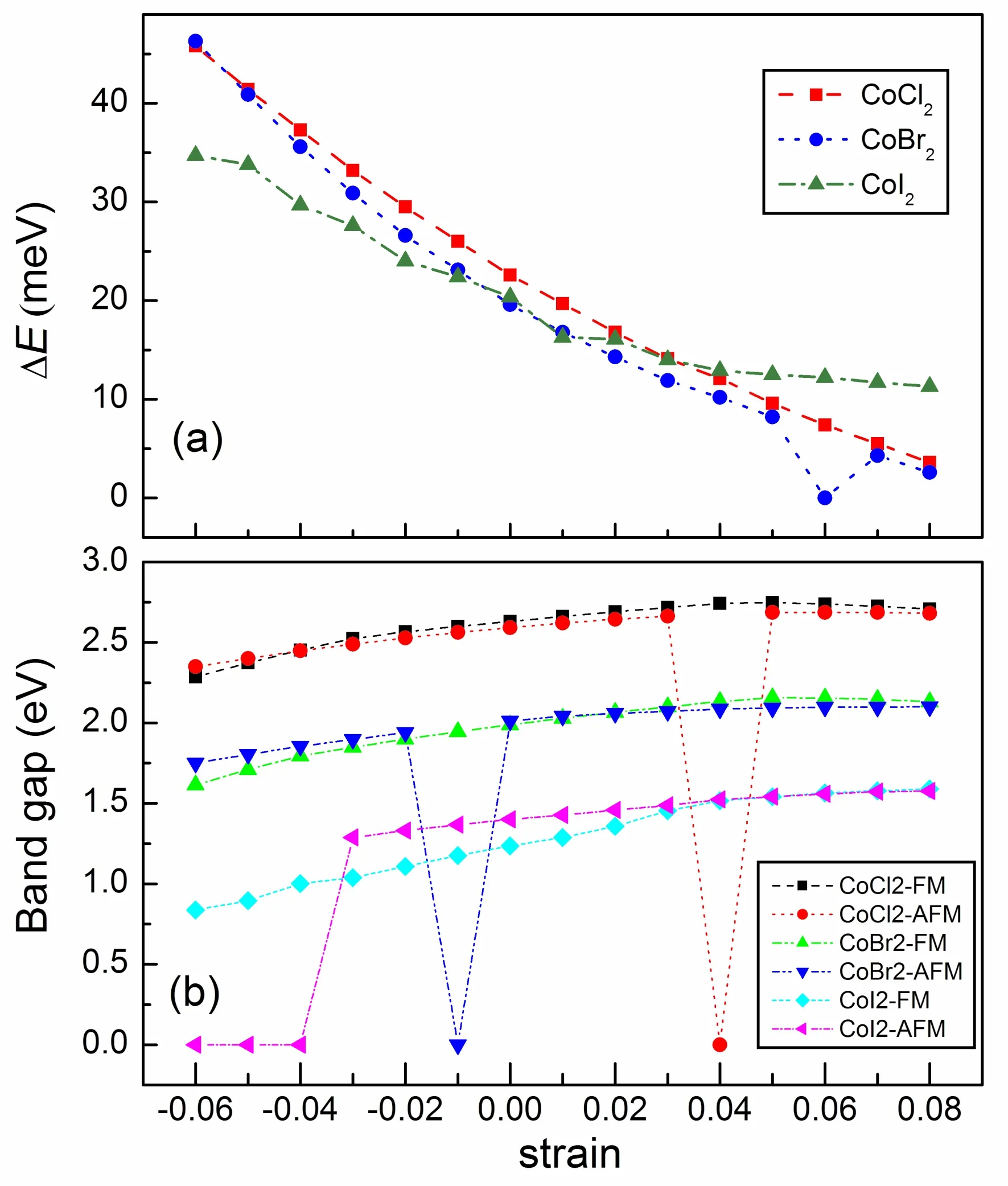
图3 铁磁态和反铁磁态的能量差(a)和能隙(b)随应变的变化图. Figure 3 The energy differences (a) and band gaps (b) of FM and AFM configurations vary with the increase of strain.
图3(b)画出了三种材料铁磁态和反铁磁态能隙随应变的变化. 对CoCl2和CoBr2材料,铁磁态和反铁磁态的能隙相差不大,并且随应变的变化很小. 对CoI2,压缩应变使得铁磁态能隙比反铁磁态能隙更快地减小.
应变除了能调节能隙的大小,更重要的是能改变能隙的特点. 研究发现,对于CoCl2,应变η≤-0.04时,体系由间接带隙半导体转变为直接带隙半导体;对于CoBr2,应变η≤-0.05时,也出现了相同的结果. 并且价带顶和导带底都在点. 图4画出了CoCl2在η=-0.04和CoBr2在η=-0.05时体系的能带图. 从图中可以看出,加应变后,两种材料的价带顶没变,但导带底移到了点,显示了直接带隙半导体特性.
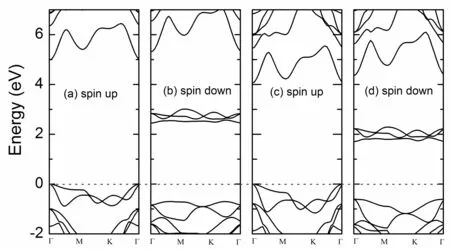
图4 CoCl2(a)、(b)和CoBr2(c)、(d)加应变后的能带图. Figure 4 Band structures of CoCl2 and CoBr2 with strain.
4 结 论
本文采用密度泛函理论系统的研究了单层金属卤化物CoX2(X=Cl、Br、I)的结构稳定性、电子性质和磁性质以及应变对能隙和磁性的调节作用. 研究发现,三种卤化物的束缚能分别是9.01、8.04和6.95 eV,表明Co原子和卤素原子间存在很强的相互作用. 能带图显示三种材料都是间接带隙半导体. 三种材料的总磁矩都是3B,主要来源于Co原子的磁矩;相邻的卤素原子的磁矩很小. 虽然三种材料的基态都是铁磁态,但是铁磁态和反铁磁态的能量差分别只有22.6、19.6和20.4 meV. 为了实现对体系物理性质的调节,我们考虑了双轴应变. 研究发现,压缩应变可以显著增强铁磁态的稳定性,并且可以实现体系由间接带隙半导体向直接带隙半导体的转变.
