压强对Zr67Ni33非晶合金结构和动力学性能的影响

2019-09-17高爱同岳星星潘诗琰申小平

原子与分子物理学报 2019年4期

高爱同，岳星星，潘诗琰，申小平，范沧

(1.南京理工大学材料科学与工程学院，南京 210094; 2.南京理工大学工程训练中心，南京 210094)

1 引言

自从非晶合金诞生以来，人们对它的研究就没有停止过[1].非晶合金具有优异的物理化学性能和力学性能如高耐腐蚀性、高强度、高硬度等，在工业和军工等领域有着广阔的应用前景[2-4]. Zr-Ni二元合金体系因其具有较好的非晶形成能力、高的热化学稳定性以及杰出的力学性能而被大量研究：Amra等人基于低温热容测量的方法研究Zr77Ni23非晶合金，发现其表现出的中间脆性、低非晶形成能力和玻色峰缺失的特征已超出了玻璃形成能力、脆性与玻色峰强度之间既定的关系[5]；Yu等人提出参数FP用来预测Zr-Ni体系的非晶形成能力[6]；Itoh 等人比较Zr39Ni61和(Zr39Ni61)D59非晶合金局域原子结构，发现两者没有主要的结构区别，表明Zr39Ni61非晶合金样品具有吸收氘的能力[7].但是关于Zr-Ni非晶合金在压强方面的研究比较少，研究表明高压可明显引起非晶合金原子间距离和化学键的变化[8-12]，影响非晶形成过程，提高非晶形成能力[13-15]，高压对体系局域原子结构演化规律和动力学性能的具体影响仍有待深入研究.随着计算机技术的发展，分子动力学(MD)方法已经广泛应用于非晶合金微观演变过程等研究，本文拟研究的非晶合金是Zr67Ni33合金体系，该成分拥有较强的非晶形成能力[16]，故我们选取Zr67Ni33成分的非晶合金来探究压强对其局域原子结构和动力学性能的影响.

2 MD模拟研究的条件和方法

本文采用经典分子动力学方法，使用开源的大规模原子/分子并行程序(LAMMPS)软件[17]进行模拟.初始结构为Zr67Ni33成分的立方原胞，总共包含6750个原子，其中Zr原子和Ni原子的个数分别为4509和2241，采用周期性边界条件和等温等压(NPT)系综，使用镶嵌原子势(EAM)[18]，数值积分方法选择Verlet算法，时间步长设置为1 fs.模拟具体过程：先将初始结构在2300 K下驰豫1 ns，获得的平衡液体分别在0 GPa、5 GPa、10 GPa、15 GPa、20 GPa下以2*1011K/s的冷却速率快速凝固到300 K，每隔100 K记录下原子的位置能量等信息供后续分析使用.

3 模拟结果与分析

3.1 结构分析

随着冷却的进行，不同压强下的Zr67Ni33平均原子势能都随温度的降低连续减少，没有发生突变，因为冷却速率快，原子来不及形成周期性重复排列结构就被冻结，液体特征被保留下来，形成非晶结构.通过计算势能温度曲线斜率转折点可以得到0 GPa、5 GPa、10 GPa、15 GPa、20 GPa下对应的玻璃转变温度(Tg)分别为753.96 K、785.82 K、801.50 K、812.77 K、817.76 K，Tg随着压强的增大而增加，在压强为0 GPa时的实验得到的Tg约为713 K[19]，模拟值高于实验值的原因：模拟的时间尺度比较短，冷却速率远大于实验条件，冷却进行的很快，因此模拟实验得到的Tg高些.

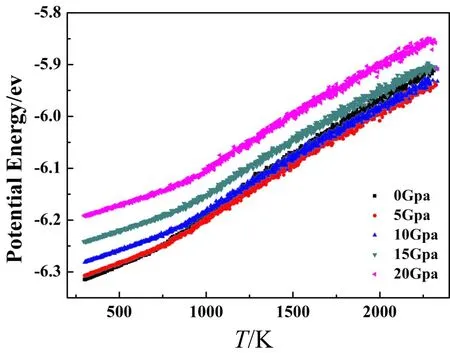
图1 不同压强下Zr67Ni33合金体系平均原子能量随温度Fig.1 Relationship between average atomic energy and temperature of Zr67Ni33 alloy system under different pressures

对分布函数(PDF)可以用来表征非晶合金的结构特征，图2表示的是0 GP时300 K下的Zr67Ni33非晶合金PDF和偏对分布函数(PPDF)，PDF的第一峰发生了相当明显的劈裂，左侧峰位置和Zr-Ni PPDF第一峰的位置接近，右侧峰位置与Zr-Zr PPDF第一峰位置接近，说明Zr67Ni33非晶合金中对其原子团簇第一近邻的贡献主要是Zr-Ni原子对和Zr-Zr原子对，并且Zr-Ni原子对所占比例最多.PDF第二峰的右侧劈裂出一个小的肩峰，而在Zr-Zr、Zr-Ni、Ni-Ni PPDF的第二峰劈裂程度更明显，证实了非晶结构存在. Zr-Zr、Zr-Ni、Ni-Ni PPDF的第一峰位对应的原子对距离分别是3.12 Å、2.67 Å、2.47 Å，而Zr-Zr、Zr-Ni、Ni-Ni原子半径之和分别为3.24 Å、2.87 Å、2.5 Å，这说明了原子间相互作用Zr-Ni > Zr-Zr > Ni-Ni，PPDF第一峰峰强也体现了这一点，Zr-Ni最高，Zr-Zr次之，Ni-Ni最低.图3是在0-20 GPa时300 K下Zr67Ni33的PDF图和PPDF图，图3(a)随着压强的增大，第一峰逐渐左移且越来越尖锐，第一波谷越来越深，说明压力的作用使得体系原子配位数增加，短程有序度增强.图3(b)-(d)中发现压强的作用都使各PPDF发生一定程度的左移，其中Zr-Zr键对左移最明显，值得注意的是Zr-Ni PPDF的第一谷几乎完全重合，这可能和Zr-Ni之间存在强烈的化学吸引作用相关.

图2 P=0 GPa下Zr67Ni33非晶合金在300 K的PDF和PPDFFig. 2 The PDF and PPDF of Zr67Ni33 amorphous alloy when P=0 GPa and T=300 K

配位数表示的是一个原子周围最近邻的原子个数，通过计算配位数可以知道体系原子排列的紧凑程度，图4是不同压强下Zr67Ni33平均配位数随温度的变化情况.随着压强增大，体系的平均配位数逐渐增大，因为压力越大，自由体积湮灭的越多，结构越来越致密.随着降温的进行，压强越大的配位数增加越缓慢.为了进一步研究分别以Zr、Ni原子作为中心原子时的配位情况.图5(a)-(d)表示的是降温过程中以Zr为中心原子周围的Zr原子、Ni原子个数和以Ni为中心周围的Zr原子、Ni原子个数变化趋势.随着温度的降低，Zr周围的Zr原子个数和Ni原子个数都逐渐增加，但是到最终状态时，压强越大，Zr周围的Zr原子个数越少，但是Ni原子个数越来越多，压力的作用使Zr周围的Zr原子个数减少的原因可能是压力越大导致Zr-Zr原子之间的斥力越大.

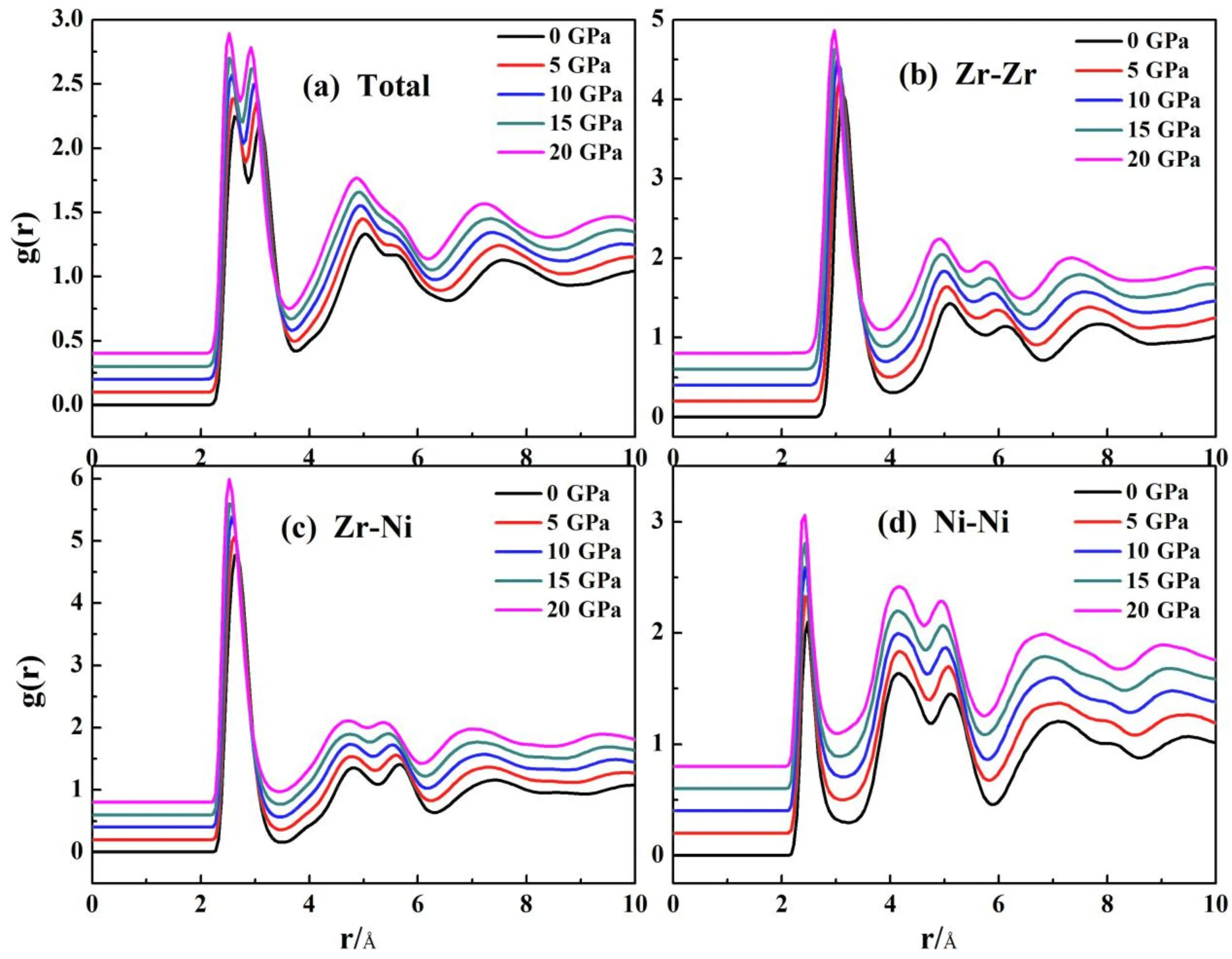
图3 T=300 K时Zr67Ni33非晶合金在不同压强的PDF和PPDFFig 3 The PDF and PPDF of Zr67Ni33amorphous alloy when T=300 K under different pressures

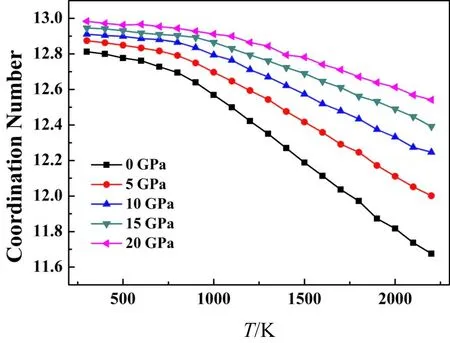
图4 不同压强下Zr67Ni33非晶合金平均配位数随温度的变化关系Fig. 4 The evolution of average coordinate number of Zr67Ni33 amorphous alloy during cooling under different pressures

而Zr周围的Ni随着压力增大而增多和Zr-Ni原子之间的强化学吸引相关.随着温度的降低，Ni周围的Zr原子逐渐增多，而Ni原子却越来越少，压力越大Ni周围的原子个数越多.

为了深入研究Zr67Ni33合金在不同压强冷却过程中的原子结构变化，采用HA键型指数法[20]，即用(ijkl)4个整数表征一个键对，如果原子a和b成键则i=1，否则i=2；j表示a、b原子周围同时和a、b原子成键的原子数量；k表示共有原子之间成键数量；l则是用来区分当i、j、k指数相同时但表征的键对结构不同时的情况.图6(a)表示的是总键对含量随温度变化分布图，其中含量最多的是1551、1541、1431键对，随着温度的降低，1551键对上升幅度最大，1541键对缓慢增加，而1431键对却缓慢降低，1441和1661键对也占一定比重并且逐渐增多，而1421和1422却呈逐渐减少趋势，20 GPa时的1551、1661、1441键对含量都比0 GPa的多，而1541、1431、1421键对含量都相应的比0 GPa时少.为了比较a原子和b原子具体是Zr和Ni谁构成时的键对含量分布不同，进一步细分，图6(b)、(c)、(d)分别表示的是a-b分别是Zr-Zr、Zr-Ni和Ni-Ni构成时的HA键对含量分布情况，在Zr-Zr偏键对分布图中含量最多的是1541键对，同时1661键对也占了一定的比重，并且增长趋势比较明显，说明Zr-Zr键对对总键对含量贡献最多的是1541键对，20Gpa时1541键对反而少.Zr-Ni偏键对键对分布图中可以看到含量最多的是1551键对，所以1551键对主要来源于Zr-Ni原子对，压力越大，Zr-Ni原子间的相互作用越强，形成1551键对的Zr-Ni原子对越多.在Ni-Ni偏键对分布含量图中最显著的就是1441键对随着温度的降低迅速增多，所以1441键主要是由Ni-Ni键形成的，文章[21]中也有相似的结论.

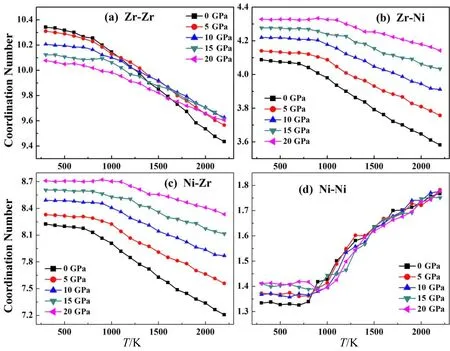
图5 (a)不同压强下Zr67Ni33非晶合金体系中Zr-Zr偏配位数随温度变化关系(b)不同压强下的Zr67Ni33非晶合金体系中Zr-Ni偏配位数随温度变化关系(c)不同压强下的Zr67Ni33非晶合金体系中Ni-Zr偏配位数随温度变化关系(d)不同压强下的Zr67Ni33非晶合金体系中Ni-Ni偏配位数随温度变化关系Fig. 5 (a) The evolution of Zr-Zr partial coordinate number of Zr67Ni33 amorphous alloy during cooling under different pressures (b) The evolution of Zr-Ni partial coordinate number of Zr67Ni33 amorphous alloy during cooling under different pressures (c) The evolution of Ni-Zr partial coordinate number of Zr67Ni33 amorphous alloy during cooling under different pressures (d) The evolution of Ni-Ni partial coordinate number of Zr67Ni33 amorphous alloy during cooling under different pressures

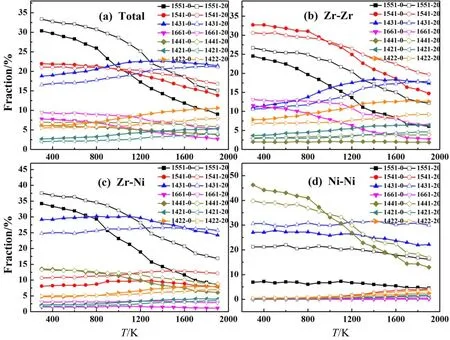
图6 (a)冷却过程中不同压强下Zr67Ni33非晶合金体系中总HA键对含量的变化；(b)冷却过程中不同压强下Zr67Ni33非晶合金体系中Zr-Zr的HA键对含量的变化；(c)冷却过程中不同压强下Zr67Ni33非晶合金体系中Zr-Ni 的HA键对含量的变化；(d)冷却过程中不同压强下Zr67Ni33非晶合金体系中Ni-Ni 的HA键对含量的变化(实心图标表示的是0 GPa，空心图标表示的是20 GPa)Fig. 6 (a) The evolution of HA bond-types of Zr67Ni33 amorphous alloy during cooling under different pressures； (b) The evolution of Zr-Zr HA bond-types of Zr67Ni33 amorphous alloy during cooling under different pressures； (c) The evolution of Zr-Ni HA bond-types of Zr67Ni33 amorphous alloy during cooling under different pressures； (d) The evolution of Ni-Ni HA bond-types of Zr67Ni33 amorphous alloy during cooling under different pressures

3.2 构型熵分析

根据Adam-Gibbs[22]理论，熵在玻璃转变中起了重要作用，过冷液体粘度的急剧升高和构型熵(S2)的降低有关，关于S2的计算公式[23]：

(1)

其中KB是Boltzmann常数，S2表示的体系的有序度，S2越低说明体系结构越有序.从图7中我们可以看到随着冷却的进行，S2逐渐降低，高压时更显著，这说明了在冷却过程中局域结构慢慢有序并且也证实了高压下的结构更为有序.

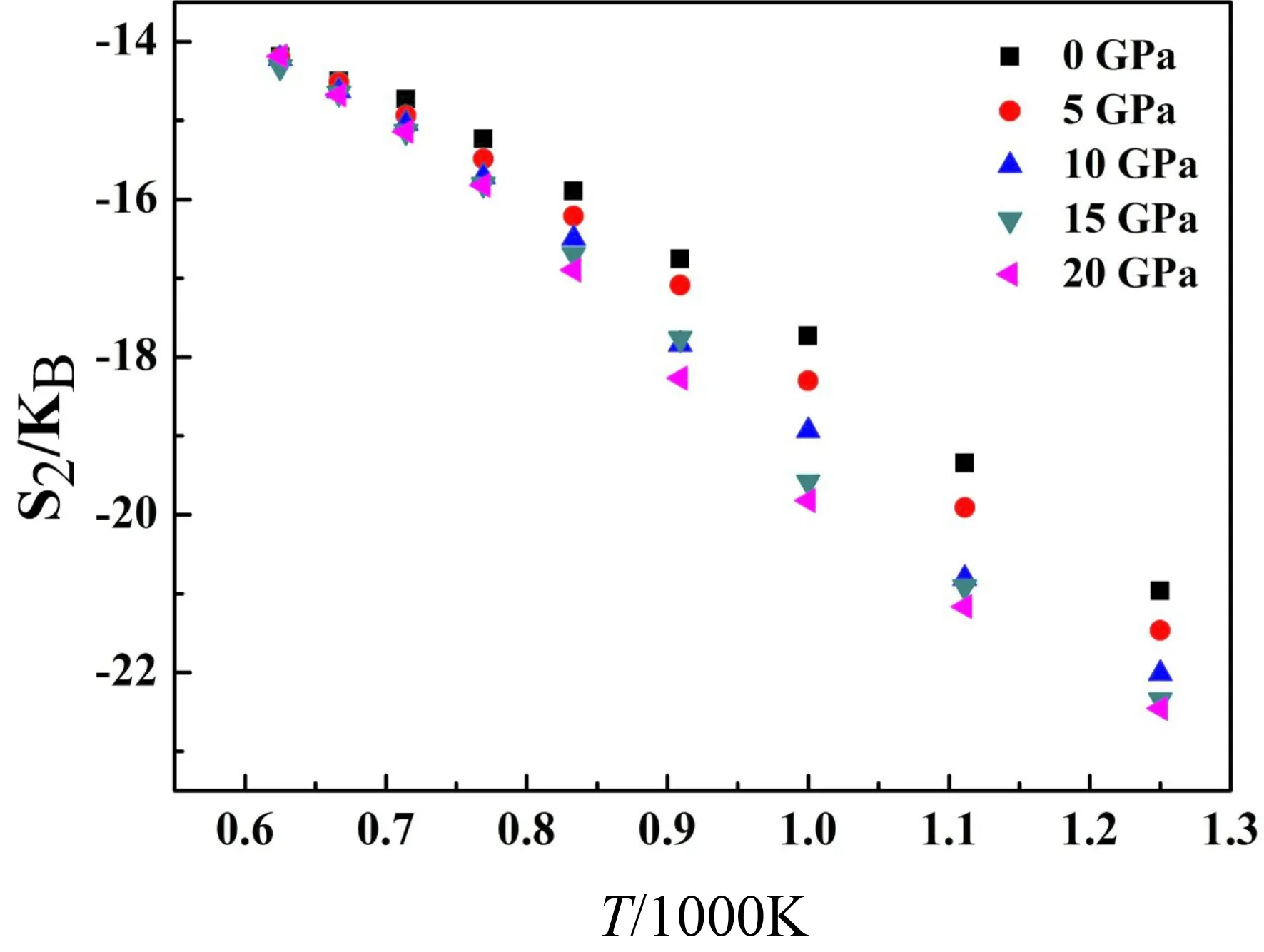
图7 不同压强下的Zr67Ni33非晶合金体系的构型熵S2随温度的关系Fig. 7 Relations of pair structural entropy S2 and temperature in Zr67Ni33 amorphous alloy systems under different pressures

3.3 动力学分析

计算均方位移(MSD)来探究压强对Zr67Ni33合金过冷液体的动力学特征的作用，均方位移函数即：

MSD=〈|ri(t+t0)-ri(t0)|2〉

(2)

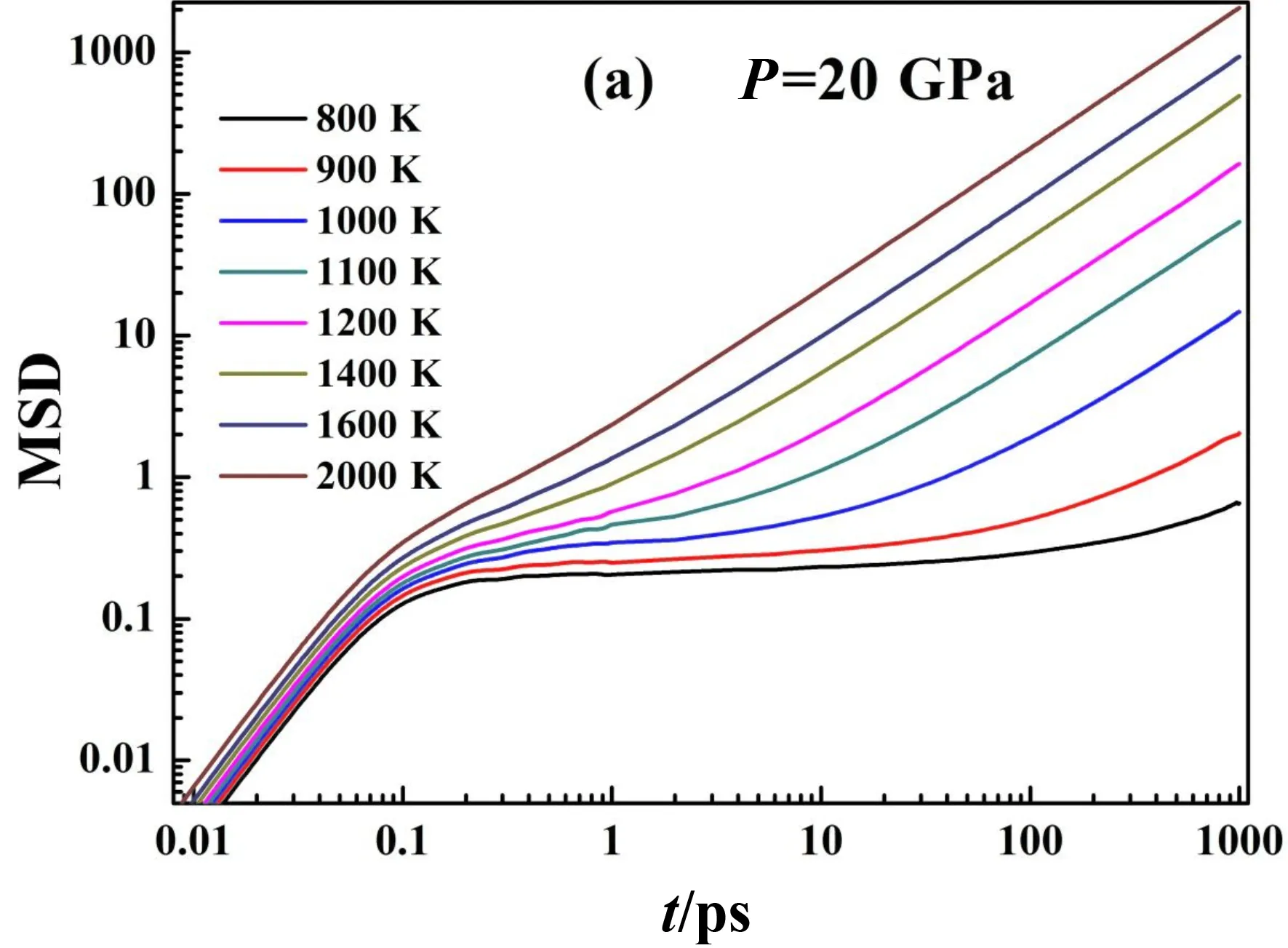
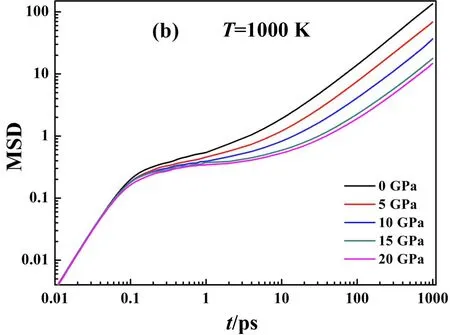
ri(t0)是i粒子在t0时刻的位移，ri(t+t0)是i粒子在t+t0时刻的位移，MSD是描述合金动力学性质的一个重要参数.图8(a)给出了20Gpa时Zr67Ni33过冷液体MSD随时间变化关系，它的曲线特征和其他文献中的合金液体的MSD类似[24]：t<0.1 ps,MSD随着时间的增加而增加，与r2成线性关系，原子没有受到任何阻力而做自由振动，原子的平均速度是由体系的热能决定的，所以相较与2000 K的MSD，800 K的MS减弱一些，低温时的原子活动能力有限，这段时间被称为初始自由振动区；当0.110 ps后，MSD与驰豫时间t几乎成正比关系，原子逃离笼子并且迅速自由扩散进入α驰豫阶段，随着温度的降低，MSD的斜率越来越小，原子扩散减慢，说明温度越低原子跑的越慢，原子的扩散行为和温度是息息相关的.图9(b)是1000 K时不同压强下的Zr67Ni33过冷液体的MSD情况，在自由振动区不同压强下的MSD几乎重合在一起，表明即使第一壳层原子堆积密度随着压强的增大而越来越致密，但是压强对自由振动区原子运动影响是微乎其微的，进入平台区后，低压的MSD高于高压的，说明平台区时高压下的密堆结构增加了原子间的相互作用力，而后进入扩散区，压力越大，对体系扩散抑制作用越强烈.通过MSD曲线可以计算出不同压强下体系的扩散系数D，如图9压力越大，扩散系数D越小，扩散越难以进行.

图8 (a) P=20 GPa时Zr67Ni33过冷液体在不同温度下的MSD随时间变化关系； (b)T为1000 K时Zr67Ni33过冷液体在不同压强下的MSD随时间变化关系Fig. 8 (a) The MSD of Zr67Ni33 supercooled liquid at different temperatures when P=20 GPa; (a)The MSD of Zr67Ni33 supercooled liquid with pressures of 0-20 GPa at 1000 K

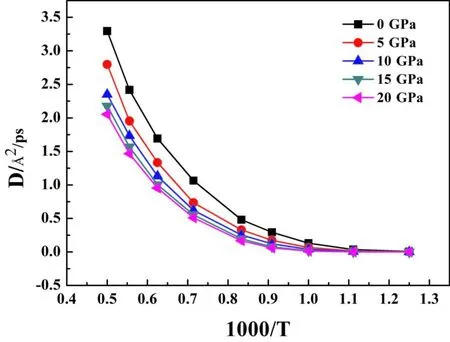
图9 在不同压强的Zr67Ni33过冷液体扩散系数D随温度的变化关系Fig. 9 Relations of diffusion coefficient D and temperature of Zr67Ni33 supercooled liquid under different pressures

为了更进一步获得Zr67Ni33过冷液体动力学信息，使用自散射关联函数(ISF)[25]，即：

(3)

N表示的是体系原子数量，ri(t)是i原子在t时刻的坐标，q为波矢，其值通常取结构因子曲线第一峰的位置.图10(a)中高温时函数很快衰减到零，而低温的ISF则经历明显的两个阶段才衰减为零并且平台特征越来越明显，平台的出现意味着β驰豫的开始，从平台衰减到0的过程称为α驰豫[26]，结果和上面MSD分析的对应.图10(b)是1000 K时不同压强下Zr67Ni33过冷液体的ISF，随着压强的增大，ISF衰减的越慢，说明原子运动越慢.温度和压强都可以使体系动力学减慢并且催使玻璃转变的发生.

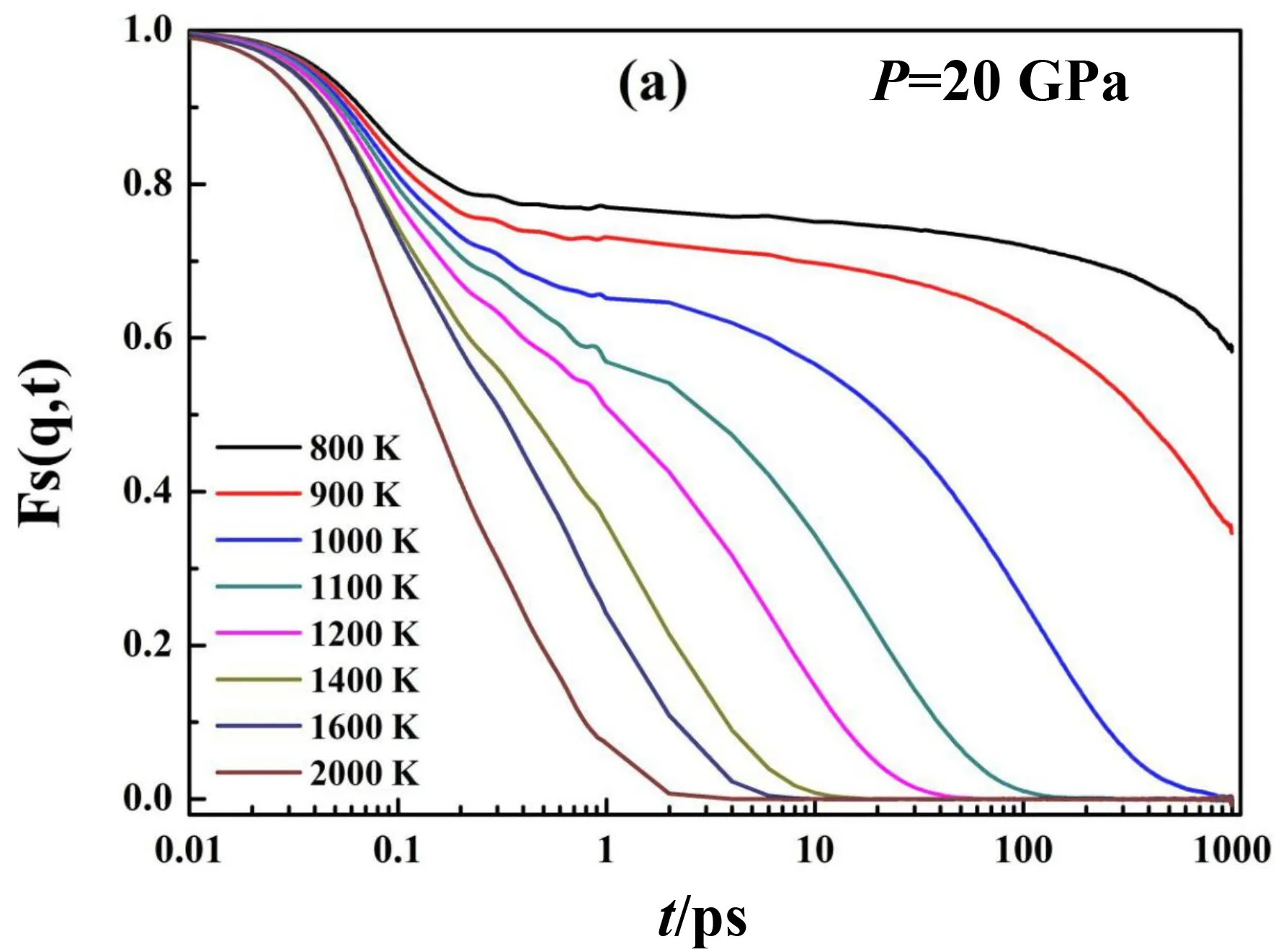
图10 (a) P=20 GPa的Zr67Ni33过冷液体在不同温度下的自散射关联函数Fig. 10 (a) The self-intermediate scattering functions of Zr67Ni33 supercooled liquid during cooling at P=20 GPa

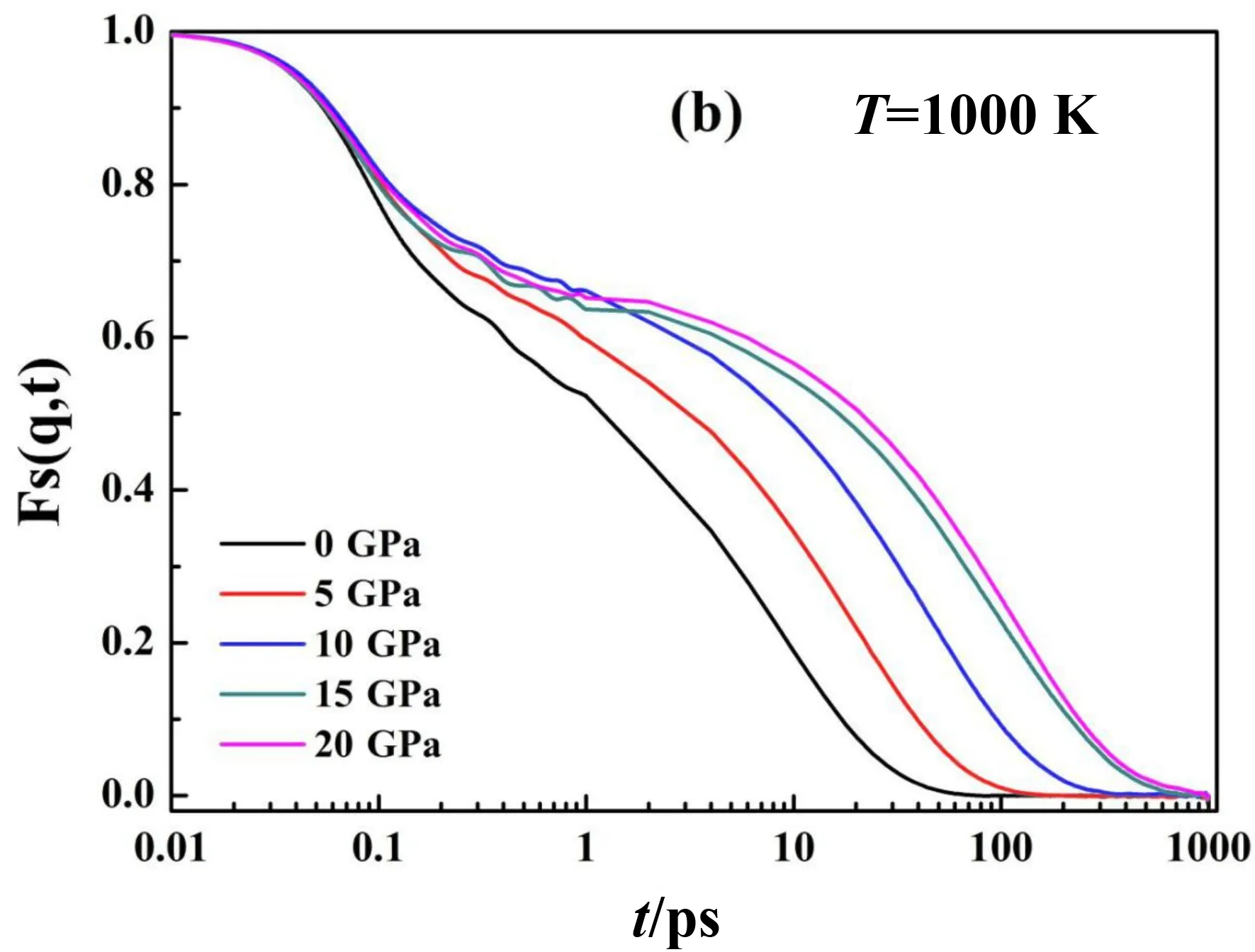
图10 (b)T=1000 K时Zr67Ni33过冷液体在不同压强下的自散射关联函数Fig. 10 (b)The self-intermediate scattering functions of Zr67Ni33 supercooled liquid during compressing at T=1000 K

图11 (a)P=20GPa的Zr67Ni33合金液体在不同温度下的非高斯参数Fig. 11 (a)The Non-Gaussian parameter of Zr67Ni33 supercooled liquid during cooling at P=20GPa

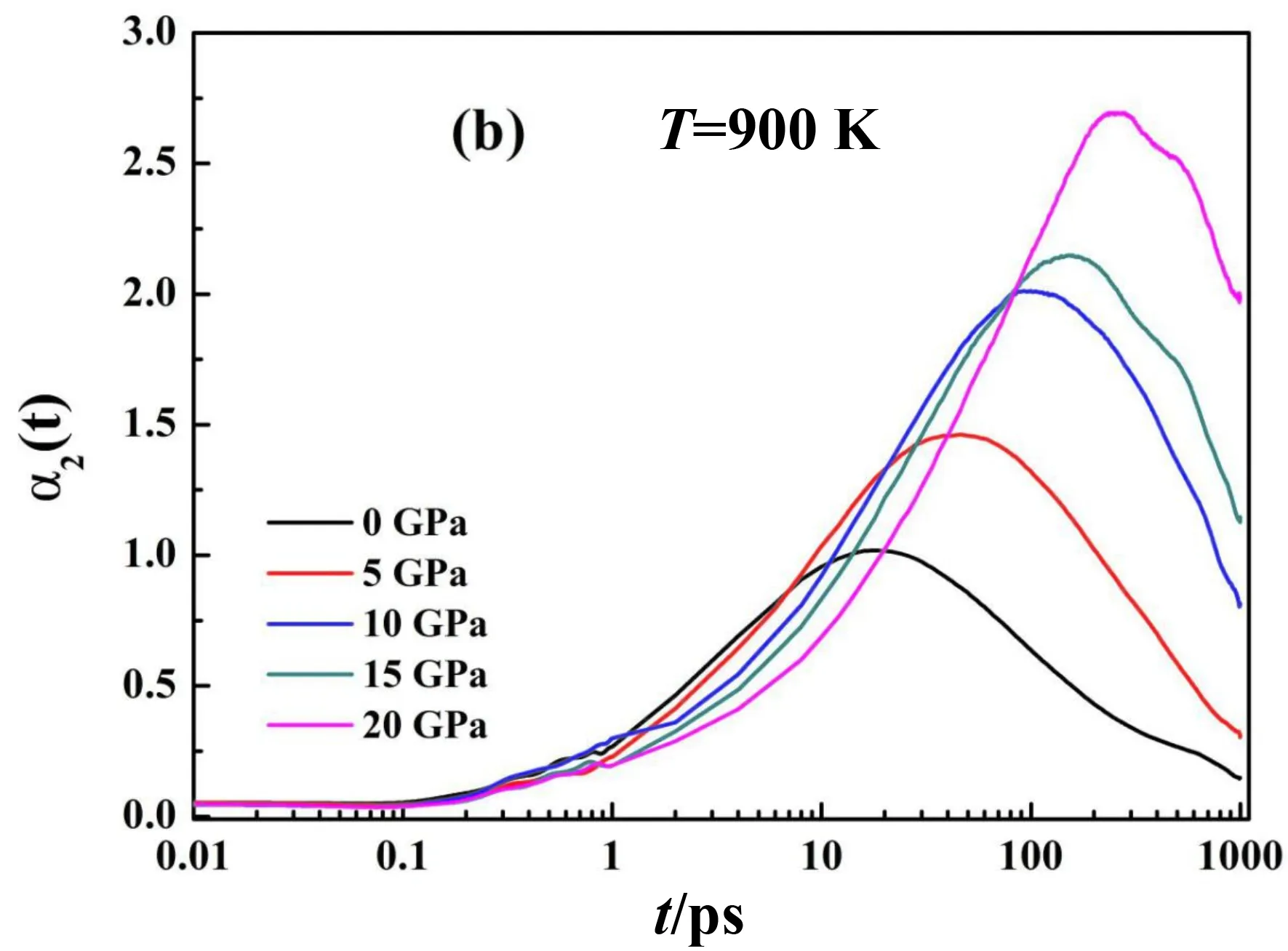
图11 (b)T=900 K时Zr67Ni33过冷液体在不同压强的非高斯参数Fig. 11 (b)The Non-Gaussian parameter of Zr67Ni33 supercooled liquid during compressing at T=900 K

非高斯参数a2[27]通常用来描述非晶合金过冷液体的动力学不均匀性，

(4)

动力学不均匀性是在一定的扩散时间段内(β驰豫)，相同时间不同原子发生的位移是不同的，从图11(a)可以看出，t<0.1 ps内，a2几乎等于0，原子作随机运动，对应着MSD的自由振动区，振动过程原子运动满足高斯分布，动力学性质基本均匀，随后a2慢慢上升，原子运动开始偏离随机状态，开始进入平台区，也就是β驰豫发生了，在不同温度下的a2曲线到达各自峰值前，他们的曲线基本是重合的，a2曲线到达峰值就意味着MSD平台区的结束，从2000 K降到800 K，非高斯参数的峰位渐渐右移并且峰值越来越高，进一步证明了随着温度的降低β驰豫时间逐渐增长，伴随着动力学不均匀性的增强.a2曲线到达峰值后的衰减过程对应着MSD的扩散区，α驰豫开始了，温度在1000 K以上时，a2曲线逐渐衰减到0，说明温度高时体系原子经过长程扩散后，扩散动力学满足高斯分布，而温度为900 K时，在所给时间内曲线衰减不到0，说明低温时体系结构驰豫不够充分，原子达不到各态历经的状态.图11(b)是900 K时Zr67Ni33不同压强下的非高斯参数随时间的变化图，随着压强的增大，a2曲线的峰位慢慢右移并且峰值逐渐升高，说明高压使得体系动力学不均匀性增强，压力对β驰豫期间笼子的出现起重要作用[28].不同温度不同压强下体系的a2曲线峰值统计如图12，温度越高动力学不均匀性越强，压强越大动力学不均匀性越强.