地理数据可用性评估指标算法及模型构建探究

(国网黄山供电公司，安徽 黄山 245000)

0 引 言

地理数据广泛应用于电力行业各类业务，包括导航地图、遥感影像、电网设备、传感器、用户等的位置信息。地理数据隐含高精度空间信息，因此地理数据在共享过程中存在着较大的安全隐患[1-2]，应进行脱密等处理。对涉密地理数据进行脱密处理包括数据抽取、几何精度降低、属性和高程处理等。其中，几何精度脱密是指使用专业脱密技术进行位移和空间位置精度随机干扰，使得脱密后的数据不易纠正恢复，避免要素泄密。

完成几何精度脱密的地理数据，是否仍然能够满足业务应用，需建立地理数据可用性评估模型[3]。通过分析地理信息数据及电网数据的使用和展示特点，构建一个综合评估模型，包括可用性评估内容分析、确定可用性评估量化因子、确定可用性评估等级等。模型用于评估脱密后数据或者通过其他变形手段变化的地理数据，是否满足应用场景需求。

1 地理数据可用性理论基础

1.1 脱密地理数据可用性问题的来源

地理数据的可用性是指地理数据被使用时，所表现出的有效性、效率和满意度[4-5]。脱密地理数据可用性问题的来源分为两部分：空间数据质量问题和脱密过程引入的可用性问题。

1.2 脱密对地理数据的影响

地理数据几何精度脱密是对地理数据的离散点坐标进行变换，其实质是建立原始地理坐标到目标地理坐标的函数映射。

几何精度脱密模型主要包括线性模型、非线性模型、混合模型、神经网络[6]。无论是采用哪种脱密模型，都能对地理数据加以不均匀的扰动，产生一定程度的影响，达到保密效果。脱密技术对地理数据的影响包括对精度的影响、对空间关系的影响以及对数据可视化效果的影响。

脱密技术对精度的影响体现在位置精度和图形精度两方面。位置精度是指空间数据表示的对象位置与现实世界中对应实体位置之间的准确度。图形精度是指空间数据中表示的对象形状与现实世界中对应实体形状之间的差异程度。

脱密技术对空间关系的影响主要体现在对空间现象的几何特性引起的空间关系，如距离、方位、连通性、相似性等。

脱密技术对地理数据可视化效果的影响，主要体现在用户对地图上以符号形式表达的地理环境信息的认识和解译的过程。由于脱密处理通常采用的是非线性方式，其对地理数据可视化产生相对较大的影响。

1.3 地理数据可用性评估内容

地理数据可用性的评估内容主要包括数据可视化效果、数据在使用时的可靠性和有效性3个方面，如图1所示。

可视化效果是指地理数据经过变化处理前后所体现出来的整体相似程度[7-8]。较低的相似度使得用户在认知信息的过程中产生错误的理解，对用户所处位置与环境产生错误的认知，从而使得地理数据的可用性降低。

使用变化处理后的地理数据时，可靠性是指要素之间的相对位置准确度。可靠性理论是建立在经典概率论基础上的，主要考虑的是随机不确定性，认为变化前后保持要素之间的相对位置是一个随机事件。

有效性则是指变化后地理数据所能提供服务正确生效的程度。对变化处理后地理数据的有效性评估主要指地理数据变化前后空间相关关系一致性。

1.4 地理数据可用性评估步骤

地理数据可用性评估分为3个步骤：1)对变化前后地理数据中要素的各个特征进行描述；2)比较变化前后要素的各特征，根据提出的评估指标依次对其进行计算，可得各指标的评估结果；3)根据特定应用特征分别赋予各指标相应的权重，在此基础上整合各指标的评估结果得到最终的评估结果。如图2所示。

图1 地理数据可用性评估内容

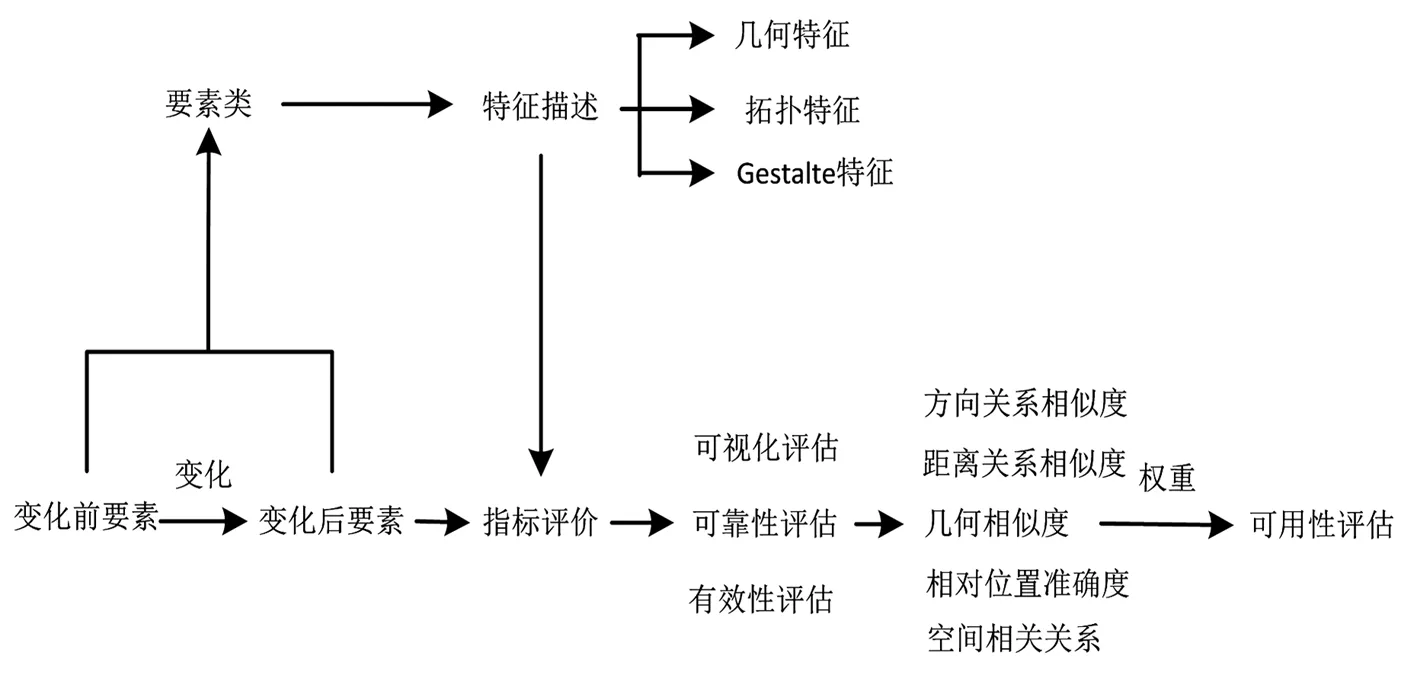
图2 地理数据可用性评估概念框架

2 地理数据可用性评估指标的度量方法

2.1 地理数据可视化度量

在地理数据中，通常用点、线、面3类数据表示各类地理实体，从而可以将地理数据划分为点群、线群和面群3类空间群组目标[9]。对于不同的空间群对象，结合变化处理对数据的影响，分别采用不同的度量方法。

2.1.1 点群目标的相似性度量

1)点群目标方向关系相似性度量

现实空间的点群分布，通常是描述带有一定的方向偏离的地理现象[10-11]。度量方法为：对目标点群生成标准差椭圆，计算其方向偏离程度来度量点群目标方向相似度，并在此基础上，根据目标点群的标准差椭圆的长、短轴之间的关系来进行点群目标距离相似度的度量。

标准差椭圆的圆心利用算术平均中心计算得到，公式为

(1)

(2)

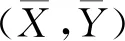
标准差椭圆的方向以x轴为准，正北方向为0°，顺时针旋转θ，计算公式为

(3)

(4)

(5)

(6)

标准差椭圆的长、短轴的长度计算公式为

(7)

(8)

对空间点群目标生成标准差椭圆，点群目标的主要分布方向可用椭圆的长轴方向进行表示。那么该方向与x轴的夹角θ的取值范围为[0，π]，则对标准差椭圆夹角分别为θ1和θ2的两个点群来说，其方向相似度为

SIMdire=|cos(θ1-θ2)|

(9)

当两点群的标准差椭圆方向相互垂直时，点群之间的空间方向相似度为0；当两点群的标准差椭圆在同一方向时，其之间的空间方向相似度为1。

2)点群要素距离关系相似性度量

点群的距离关系可用点群中要素的集中程度来表示，采用标准差的长、短轴的距离之比来描述[12]。对标准差椭圆长、短轴分别为a1、b1和a2、b2的两个点群来说，定义其距离相似度为

(10)

3)点群要素几何特征相似性度量

对于空间点群要素的几何特征描述，主要是通过点群分布范围来对空间点群目标的几何相似性进行度量[13]。考虑到分布范围相似度的度量需要具有旋转、平移和缩放不变性，提出了一种形状描述函数来计算面要素之间的形状相似度。

(11)

式中，f(li)为点群最小外包多边形的描述参数，即点群外包多边形各点到形心点的距离。

4)点群要素综合相似性度量

考虑到空间要素间的空间关系和几何特征分布，通过其对空间点群要素相似度的影响进行分析，因此对前述3个相似度度量指标分别赋以0.4、0.3、0.3的权值，得到点要素的综合相似度计算公式为

Spoi=0.4SIMdire+0.3SIMdist+0.3SIMscope

(12)

2.1.2 线群要素的相似性度量

1)线群要素方向关系相似性度量

利用解析几何的方法，采用独立于空间线状要素之外的直接坐标系对线状要素整体进行统计，计算整个线群要素的方向均值，利用方向均值的象限角度对线群要素的空间方向关系进行定量描述[14]。方向均值的计算公式为

(13)

式中：θv为各个线要素的方向；θR为线群要素的方向均值。

若变化前后线群要素的方向均值分别为θ1与θ2，那么两组线群要素的空间方向关系相似度的计算方法为

Simdir=cos|θ1-θ2|

(14)

2)线群要素距离关系相似性度量

用空间线群要素的空间距离关系相似度来描述各个要素之间方向关系的不一致性程度[15]。用环形方差来对方向距离关系进行度量。计算公式为

(15)

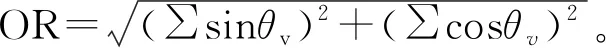
环形方差即线群距离关系的值域在0和1之间。当OR=0时，表明线群的集中方向之间的距离为0；当OR=1时，认为各要素与线群的整体方向的距离最远。那么距离相似度计算方法为

(16)

3)线群要素几何特征相似性度量

线群要素几何特征可用曲折度描述。线的曲折度可简单定义为线的实际长度和其直线长度的比值[16]。实际长度用坐标串中点与点之间的直线距离累加来近似计算。其计算公式为

(17)

式中：L为线要素的长度；S为线要素首尾端点的直线距离。那么可以计算线群要素1和要素2的几何相似度，计算方法为

(18)

4)线群要素综合相似性度量

考虑到空间要素间的空间关系和几何特征分布，通过其对空间线群要素相似度的影响分析，分别对前述计算出的3个相似度分别赋0.4、0.2、0.4的权值。那么线要素的综合相似度计算公式为

Spline=0.4Simdire+0.2Simdist+0.4Simgeo

(19)

2.1.3 面群要素的相似性度量

1)面群要素方向关系、距离关系相似性度量

空间面群要素多为比较规则的面状要素，因此可生成其最小面积外接矩形，如图3所示。该面状要素的方向就是其最小外接矩形的最长边的方向，则可将二维的面状要素降维至一维的线状要素[17]。

图3 多边形最小面积外接矩形

2)面群要素几何特征相似性度量

面状要素的几何特征值采用紧致度来描述[18]。紧致度用来描述一个给定的多边形区域离某一特定形状的面的偏离程度。面的紧致度采用其面积与周长之间的比率描述。对于多边形X，其紧致度C(X)为

(20)

式中:P(Xi)为多边形Xi的周长;Are(Xi)为多边形的面积。那么，空间面群要素的几何相似度为

(21)

3)面群要素综合相似性度量

考虑到空间要素间的空间关系和几何特征分布，通过其对空间线群要素相似度的影响分析，对前述计算出的3个相似度分别赋0.3、0.3、0.4的权值。面要素的综合相似度计算公式为

Spgone=0.3Simdire+0.3Simdist+0.4Simgeo

(22)

2.1.4 地理数据的综合相似性度量

人们是基于背景要素来获取其所处的空间位置，因此在对地理数据变化前后整体相似性度量时，应分别对点、线、面要素赋予不同的权值，即0.2、0.3、0.5。那么，变化前后地理数据的可视化度量模型为

Sim=(0.2Spoi+0.3Spline+0.5Spgone)×100

(23)

2.2 地理数据可靠性度量

相对位置准确度就是各地理要素在变化前后，其相对位置变化程度[19]。变化前随机选取多边形区域Si，在此区域中随机选取mi个点，经过处理后，得到对应的Si′、mi′，其中处理后仍在Si′区域中的点数为mi″。相对位置准确度计算公式为

(24)

式中，n表示随机选取的区域个数。

那么，变化前后地理数据可靠性度量模型为

W=100×Ac

(25)

式中，W表示地理数据可靠性综合评分。

2.3 地理数据有效性度量

变化前后空间相关关系一致性是指要素间的空间相关关系在处理后得到的保持和延续。因为组成线、面的点空间相关关系不变，则线、面的空间相关关系也保持不变。因此，在采样点的规模足够大的情况下，空间相关关系一致性只考虑点要素的空间相关关系。

设抽象前的地理空间场景为DB，其中的空间要素集合为OB1，OB2，…，OBn，各个空间要素之间的拓扑关系分别为r(OBi，OBj)(1≤i

在对变化前后地理数据进行空间相关关系评估时，首先确定评估目标，并确定对应的空间要素。对于确定的空间场景DB和DA，其中任意两个要素之间的关系r(OBi，OBj)和r(OAi，OAj)都是已知的，那么就可以将它们的关系进行比较，判断它们之间的空间相关关系是否得到保持。若关系等价的，则认为空间相关关系一致，此时空间相关关系一致性为1。若关系不等价，则认为空间相关关系不一致，此时一致性为0，即有：

EQU(r(OAi,OAj),r(OBi,OBj))

(26)

这样通过计算变化前后地理数据要素之间的空间相关关系一致性程度，可以确定变化前后场景DB和DA之间的空间相关关系一致性大小。计算公式为

E=EQU(DB,DA)

(27)

那么地理数据的有效性度量计算公式为

Eff=E×100

(28)

3 地理数据可用性评估模型

地理数据可用性评估的目的是对地理数据的处理(脱密等)结果进行分析与评估,其评估结果可表明处理后的地理数据的可用性，可用性评估越高说明其处理技术越优，处理结果越准确[20]。可将其反馈给处理(脱密等)过程中的各个环节,对处理技术进行调控和整改 ,从而得到高可用性的处理成果。

根据地理数据的可用性评估内容,可用性评估涉及到可视化效果、可靠性及有效性三方面,因此地理数据可用性评估应综合考虑这三方面的影响。由于各个指标在评估中的重要性并不完全相同,可赋予一定的权重对地理数据可用性进行综合评估。

在对地理数据进行可用性综合评估前，要对其进行可用性检测，规则如下：

1)地理数据可视化效果评价指标，在评估过程中，综合相似度计算结果低于85时，认定数据视觉效果严重失真，评定该地理数据可用性为不合格。

2)地理数据可靠性评价指标，采样规模庞大时，结果低于95，则会出现变化前后地理数据中大量点、面相对位置关系不一致的情况，不能满足电力行业的应用需求，认定为不合格。

3)地理数据有效性评价指标，在采样规模庞大时，结果低于95，则会出现变化前后地理数据中大量点、点空间相关关系不一致的情况，导致线、面的空间相关关系也出现不一致的情况，对地理数据的使用产生误导，认定为不合格。

除了上述指标评价之外，对地理数据进行敏感性检查，若存在不符合国家相关规定的要素，则评定该地理数据可用性为不合格。

当对地理数据的可用性评估通过以上检测时,可对地理数据进行综合评估,基于业务需求与相关标准以及处理技术特点,分析可视化效果、可靠性、有效性对地理数据可用性的影响,分别对其赋予权值并进行计算,其计算方式为

Q=Sim×0.2+W×0.4+Eff×0.4

(29)

式中：Sim表示可视化效果度量结果；W表示可靠性度量结果；Eff表示有效性度量结果。

根据相关要求与规定及用户需求,将地理数据可用性分为4个等级,分别是优秀、良好、合格和不合格。各可用性等级对应的评分值见表1。

表1 地理数据可用性的平直区间表

4 地理数据可用性评估实验

4.1 概述

实验所采用的数据为某公园附近1:10 000地图地理数据,实验数据所涉及的区域约1.93 km2,采用相对独立坐标系,按要素类型可分为点要素、线要素、面要素，如图4所示。

4.2 实验与分析

首先对脱密地理数据进行检查,检查的内容包括数据敏感要素、数据格式、数据组织、完整性、逻辑一致性、位置准确度、专题准确度、时间准确度等等。然后依据可用性度量模型将检测结果转化为对地理数据可用性元素的度量,最后计算出地理数据可用性综合评估结果。下面以模型A(自主研发地理数据脱密算法)为例进行计算说明。

图4 实验数据示意

1)脱密前后可视化计标计算

脱密前后可视化指标计算如表2所示。

表2 脱密地理数据可视化效果评估表

从表2中的计算结果来看,各类要素各项指标的相似度相对较高,表明此脱密较好地保证了脱密前后地理数据空间方向、空间距离及几何相似性。脱密前后地理数据综合相似度为99.55，表明此脱密算法较好地保持了空间方向、空间距离、图形几何等特征内容,评测结果与人的视觉一致。

2)脱密前后可靠性指标计算

在试验区域随机选取2个面要素与其中的10个点要素，根据可靠性计算方法得到评估结论，如表3所示。

表3 脱密地理数据可靠性评估表

3)脱密前后有效性指标计算

在试验区域选取100点要素作为采集对象进行有效性计算。通过计算发现，脱密后未出现点要素之间的拓扑关系不一致，因此脱密前后拓扑关系一致性为1，有效性指标结果为100。

4)脱密地理数据综合可用性评估与分析

根据第3节给出的方法,对脱密地理数据的可用性进行综合评估,可用性得分为99.91。那么可认定采用模型A对地理数据脱密处理后,数据的可用性评估为优秀。

5 结 语

在对地理数据可用性基本理论和地理数据脱密理论分析的基础上，对地理数据(主要针对脱密处理)的可用性评估进行剖析，研究了地理数据可用性概念框架，并根据脱密地理数据可用性问题来源，提出了基于可视化效果、可靠性、有效性的可用性综合评估模型。所提研究可量化评估地理数据的可用性，并根据地理数据可用性评估结果预判其在应用场景中的可用性。