融合智能代理模型和改进微分进化算法的电力系统暂态稳定预防控制

陈 振，韩晓言2，范成围，张 华，刘 畅

(1.国网四川省电力公司电力科学研究院，四川 成都 610041;2.国网四川省电力公司，四川 成都 610041)

0 引 言

随着电力市场改革不断深入以及电网互联规模增大，系统的运行方式越来越趋于稳定极限，暂态稳定问题愈发突出[1-2]。暂态稳定预防控制(transient stability preventive control，TSPC)是指在预想故障状态下，通过调整系统稳态运行点提高安全稳定裕度，保证系统暂态稳定的同时确保系统某一经济性指标最优。从数学的角度看，可表示为考虑暂态稳定约束的最优潮流模型[3]。TSPC模型属于动态优化范畴，即包含微分方程的非线性规划问题，求解困难。因此，开发一种寻优能力强且计算代价小的TSPC模型求解算法十分重要。

传统的TSPC求解方法，如数值差分方法和交互迭代方法，均采用动态规划或者内点法求解优化问题，这类方法在寻优时依赖于优化问题的凸特性[4-8]。随着系统复杂程度的增加和优化模型中考虑因素的增多，TSPC问题逐渐呈现出非凸性和不连续性的特点，传统方法在求解时面临较大困难[9]。智能优化算法又具有全局寻优性能强以及通用性强等特点，能有效弥补传统方法的不足，适用于有效求解大规模、复杂的优化问题。

微分进化(differential evolution，DE)算法属于众多智能优化中的一种，具有寻优能力强和运行速度快的特点。文献[10]将DE算法应用于TSPC的求解中，取得不错的效果。然而，基于标准DE算法的TSPC求解仍然面临以下2个问题：1)标准DE算法的变异操作和参数在寻优过程中保持不变，缺乏对优化算法全局搜索和局部搜索的平衡；2)由于在每次优化迭代过程中，需要对系统的暂态稳定状态进行判定，传统方法通常采用时域仿真方法进行稳定分析，时间开销巨大。

针对上述问题，提出融合代理模型和改进微分进化算法的预防控制优化模型求解方法。在标准DE的基础上，引入扩展变异操作及参数自适应调整策略，提高微分进化算法的寻优能力，并利用改进微分进化算法(improved differential evolution，IDE)求解预防控制优化模型。同时，为提高TSPC的求解速度，在离线阶段，利用潮流特征和集成极限学习机(ensemble extreme learning machine, EELM)建立暂态稳定裕度预测的智能代理模型[11]，快速判定给定运行方式下系统的暂态稳定裕度，避免迭代过程中需要反复进行时域仿真的缺点，大大降低了寻优过程的计算代价。仿真结果证明了所提方法的有效性和快速性。

1 暂态稳定预防控制的数学模型

1.1 目标函数

TSPC目标函数的形式很多，以考虑阀点效应的发电机运行成本为目标函数[12]，可表示为

(1)

式中：Pgi为发电机i的有功出力；NG为可调发电机集合；ai、bi、ci、ei和wi分别为考虑阀点效应后发电机i的发电成本系数。

由式(1)可见，考虑阀点效应后，发电机的运行成本在原来二次函数的基础上加上了类正弦项。由于此目标函数存在三角函数和绝对值运算，因而优化模型呈非凸特性。

1.2 等式约束

TSPC模型的等式约束为系统的潮流方程，以极坐标的方式表示系统的潮流方程。

(2)

(3)

式中：N为总节点数；Pgi和Qgi分别为节点i的有功、无功注入功率；Pdi和Qdi分别为节点i的有功负荷与无功负荷；θij为节点i和节点j的相角差；Gij和Bij分别为节点i和节点j之间的电导和电纳。

1.3 不等式约束

1)有功出力约束

(4)

2)无功出力约束

(5)

3)节点电压约束

(6)

4)支路功率约束

(7)

式中：Si为线路i的视在功率；Nl和Ng分别为支路总数和发电机总数。

5)暂态稳定约束

暂态稳定约束具有多种表达形式，这里采用基于临界切除时间(critical clearing time，CCT)的表示方法。若系统在给定故障状态下失稳，通过改变系统的运行状态提高此故障的CCT大小，使CCT大于故障持续时间，从而保证系统的暂态稳定。为使系统具有一定的稳定裕度，常使CCT稍大于故障持续时间。

在利用智能优化算法求解TSPC问题时，需要反复计算CCT的大小，若采用时域仿真的方法，时间开销巨大。因此，在离线阶段，利用系统的潮流特征和EELM建立暂态稳定裕度预测的智能代理模型，从而在优化求解过程中大幅度减小时间开销。智能代理模型的构建过程详见文献[11]。

暂态稳定约束可表示为

tpc-td≥tm

(8)

式中：tpc为预测的CCT值；td为故障持续时间；tm为给定的时间裕度，取大于0的常数。考虑到EELM代理模型存在预测误差，可适当增大时间裕度值，确保优化结果的可靠性，这里中tm取为0.01 s。

2 改进微分进化算法

良好的搜索策略应该是在搜索的初始阶段保持种群的多样性，进行全局搜索，而在搜索后期加强局部搜索能力，以提高算法的精度和收敛速度[13]。

根据此原则，从扩展变异操作与参数自适应调整两方面对标准DE算法进行改进，形成改进微分进化算法，平衡寻优过程中的全局搜索和局部搜索能力。

2.1 微分进化算法基本原理

DE算法利用随机选取的矢量参数的差向量作为新矢量参数的随机变化源，通过对当前种群进行交叉、变异和选择等操作产生新一代种群，并逐步使种群进化到最优解[14]。主要包含以下几个步骤：

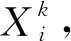
(9)

式中：r1、r2、r3属于[1,NP]之间随机产生的整数，且与目标向量的索引号i不同；系数F为缩放因子。

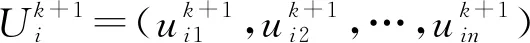
(10)

式中：qj为[1,n]中随机选取的一个整数，用以保证每轮试验向量至少有一维变量由变异向量提供；交叉因子CR的取值范围为[0,1]。

3)选择。采用一种贪婪的选择模式，以最小化问题为例，可表示为

(11)

2.2 改进微分进化算法

1)扩展变异操作。标准DE算法的变异操作采用3个完全随机的个体组成，可增加种群的多样性，具有较强的全局搜索能力，但收敛速度慢。可对标准DE算法的变异操作进行自适应扩展，形成新的变异操作方程为

(12)

式中，α=k/NI，k为当前迭代数，NI为最大迭代次数。

从新的变异操作方程可知，在搜索初期，变异操作主要由随机个体引导，因此具有较强的全局搜索能力，随机进化代数的不断增大，逐渐过渡为由最优个体进行引导，算法的局部搜索能力增强，从而增加收敛精度，加快收敛速度。

2)参数自适应调整。缩放因子F和交叉因子CR是DE算法的主要参数，其值大小对于DE的寻优性能具有重要影响。在标准的DE算法中，整个搜索群体共享一个F和CR的值，且在进化过程中，F和CR均保持不变，影响DE的搜索性能。因此，对参数F和CR分别提出自适应调整策略，可有效提高算法的寻优能力。

(13)

(14)

式中：CRmax和CRmin分别为CR的最大值和最小值；φ2为给定系数，这里取为3。

3 TSPC优化模型求解流程

3.1 种群初始化与约束条件处理

1)种群初始化。求解TSPC问题首先需要对种群进行初始化，需要进行初始化的变量包括除去平衡节点发电机有功功率和所有发电机的电压幅值。初始化的个体i可表示为

Xi=[Pi,g1,...,Pi,gNg-1,Vi,g1,...,Vi,gNg]

(15)

在随机初始化后，需要对种群中的个体进行潮流计算，考虑到平衡机有功出力的上下限，为避免生成潮流不收敛的个体，需要对初始化后的种群进行筛选，剔除不满足有功平衡的个体，并重新初始化，提高迭代过程的搜索效率。满足以下两个公式中任意一个的个体将会被剔除：

(16)

(17)

2)约束条件处理。种群初始化后，对其中的每个个体进行潮流计算，为了使潮流结果的值满足不等式约束和暂态稳定约束，可采用罚函数法处理不等式约束，其基本思想是将约束条件引入目标函数中作为一个新的函数，将有约束的优化问题转化为无约束优化问题。

3.2 TSPC求解流程

所提IDE-EELM方法综合利用智能优化和智能预测算法的特点，利用IDE算法寻优能力强的特点在解空间进行搜索，并利用EELM智能代理模型的快速性和准确性对IDE算法搜索的解进行暂态稳定判定，并将判定结果以惩罚值的形式反馈给IDE算法，引导其进一步搜索。

基于IDE-EELM的TSPC优化流程如下：

1)参数设置。输入系统数据、变量上下限及故障信息。设置IDE算法初始参数，包括种群规模NP、最大迭代次数NI及控制参数F和CR的上下限等。

2)初始化种群。随机生成初始种群，对每个初始种群进行有功平衡校验，若不满足校验则重新生成，直到生成NP个解。

3)计算每个个体的潮流，将潮流结果作为输入特征，应用EELM代理模型预测当前运行状态下的CCT，并判定系统暂态稳定性。根据潮流信息和暂态稳定信息计算个体的适应度函数值；记录群体中的最优解。

4)令迭代次数k为1。

5)判断当前迭代次数k是否达到最大迭代次数NI，若未达到最大迭代次数，则转至步骤6)；否则结束迭代，转为步骤9)。

6)根据目前的迭代次数确定缩放因子F和交叉因子CR的大小并进行扩展变异操作，经过变异后，需要对控制变量进行校验，避免控制变量越限；根据交叉因子大小进行交叉操作。

7)调整罚函数系数，计算新生成个体的适应度函数值；记录群体最优解。

8)利用贪婪策略对个体进行选择，迭代次数k+1；转至步骤5)。

9)输出最优解对应结果。

计算流程如图1所示。

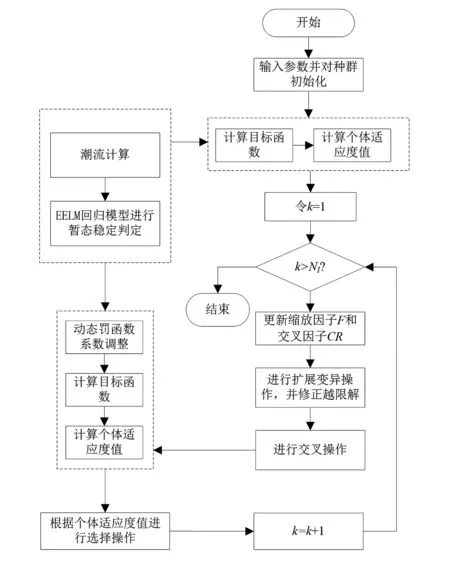
图1 TSPC优化模型求解流程

4 算例分析

以新英格兰39节点系统为例对所提方法进行仿真验证，发电机的成本系数来自文献[15]，不等式约束中各变量的限值来自文献[16]。系统单线图如图2所示。

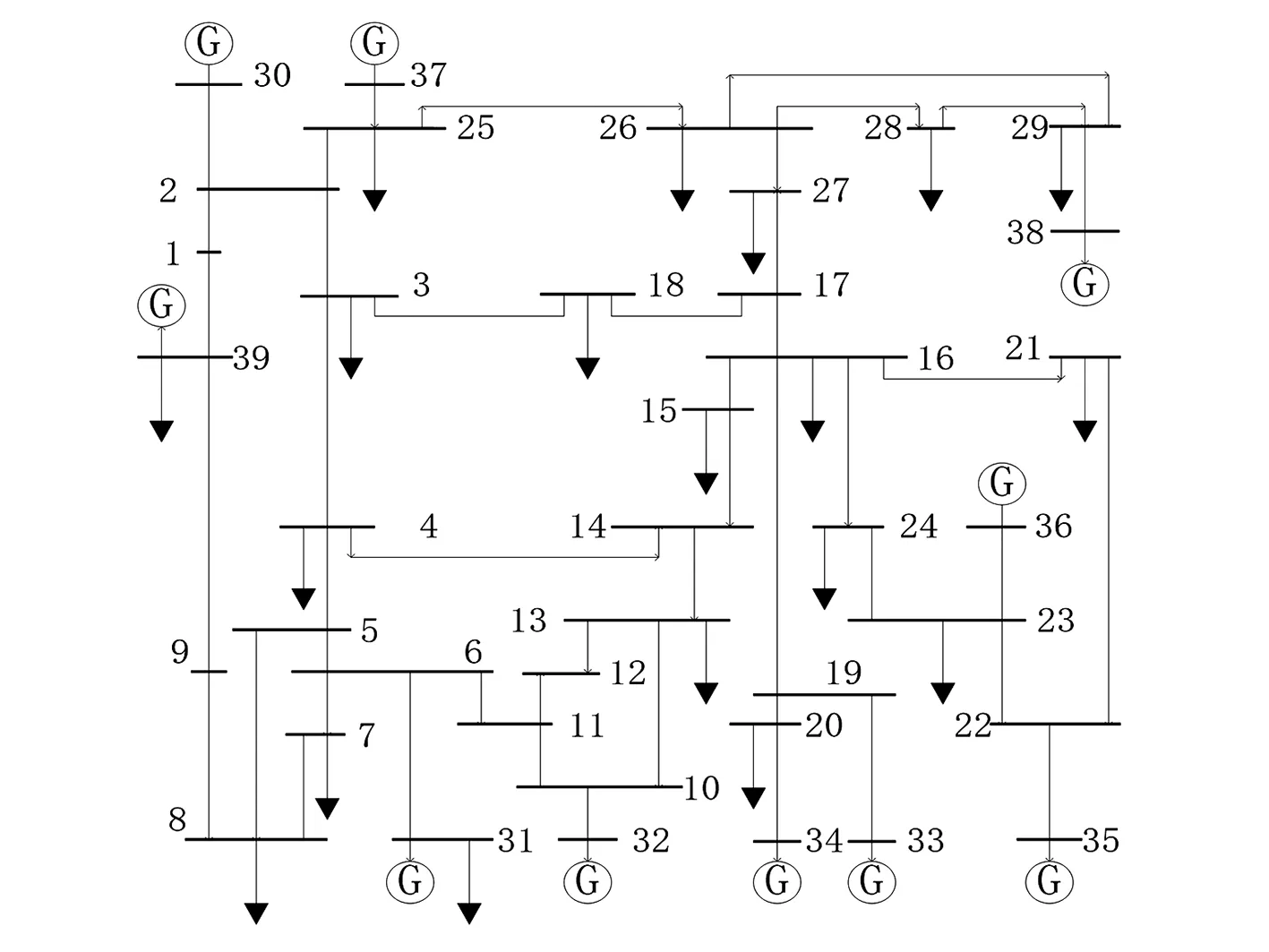
图2 新英格兰39节点系统单线

预想故障集包含以下2种故障。

预想故障1：故障节点为2号母线，切除线路2-3，故障发生时间为0.1 s，故障切除时间为0.28 s。

预想故障2：故障节点为15号母线，切除线路15-16，故障发生时间0.1 s，故障切除时间为0.25 s。

根据上述预想故障，考虑以下3种TSPC模型：

模型1：仅考虑故障1的TSPC模型。

模型2：仅考虑故障2的TSPC模型。

模型3：同时考虑故障1和故障2的TSPC模型。

前两种模型称为考虑单重预想故障的TSPC模型，第3种模型为考虑多重预想故障的TSPC模型。

首先对IDE-EELM算法的有效性进行仿真分析。将所提方法应用于求解上述3种TSPC模型，并将结果与PSO-EELM算法和DE-EELM算法的计算结果进行对比。

3种优化算法的参数分别为：IDE算法中，缩放因子取值的最大值和最小值分别为0.9和0.4，交叉因子取值的最大值和最小值分别为0.8和0.3；DE算法中，缩放因子和交叉因子分别固定为0.6和0.5；PSO算法中，采用线性递减的惯性权重，惯性权重的最大值和最小值分别为1.2和0.4，加速因子均取为2。3种方法的种群个数均为30，最大迭代次数均为50次[9]。EELM智能代理模型的参数见文献[11]。为考虑算法的随机性，同一模型均进行10次重复试验。

4.1 预防控制策略有效性分析

根据所提算法的优化结果，验证预防控制策略的有效性，如图3所示。

图3 3种模型下的预防前后控制对比

图3(a)和图3(b)为传统最优潮流下和暂态稳定约束最优潮流下故障1分别发生时的功角曲线，图3(c)和图3(d)为传统最优潮流下和暂态稳定约束最优潮流下故障2分别发生时的功角曲线，图3(e)和图3(f)为暂态稳定约束最优潮流下同时考虑故障1和故障2的功角曲线。

由图3可见，不论是单重故障还是多重故障，所提方法均能有效抑制电网在预想故障下的暂态失稳现象。

4.2 算法性能对比

对比3种优化算法(IDE-EELM、 PSO-EELM、和DE-EELM)的结果见表1，主要对比了3种算法的平均费用。

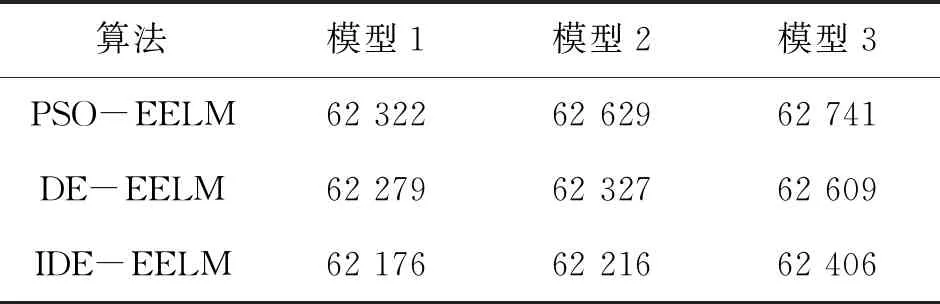
表1 3种算法的平均费用 单位：$/h

由表1可知，3种模型下，IDE-EELM算法求解得到的平均费用均优于PSO-EELM算法和DE-EELM算法。

4.3 时间开销分析

传统基于智能优化算法求解TSPC模型时采用时域仿真法(time domain simulation，TDS)对暂态稳定性进行判定，为降低时域仿真的计算开销，往往需要设置一个较短的仿真时长和较小的功角阈值。

表2给出了3种模型下，IDE-EELM算法的求解时间tAE与IDE-TDS算法求解时间tAT的对比情况，IDE优化算法的参数如前所述，TDS的参数来自文献[16]，仿真分析的计算机配置参数为：Inter core i7 CPU @2.5 GHz，8 G内存，暂态稳定时域仿真软件为PST 3.0。

表2 计算时间对比

由表2可知：1)在求解单重预想故障和多重预想故障时，IDE-EELM算法的计算时间增长不明显，而IDE-TDS算法的计算时间几乎是成倍增长；2)在3种模型下，IDE-EELM算法的计算时间相对于IDE-TDS算法的计算时间分别减少了98.49%、98.58%和99.11%，说明IDE-EELM算法可大幅度降低TSPC模型求解的计算时间。

5 结 语

提出一种融合智能代理模型和改进微分进化算法的TSPC求解方法，综合利用IDE算法优良的寻优能力和EELM智能代理模型快速的暂态稳定能力进行优化模型的求解，通过在新英格兰39节点系统的仿真分析，可得结论如下：

1)相比于传统的两种智能优化算法，无论在单重预想故障还是多重预想故障下，IDE-EELM算法均能在保证系统暂态稳定的前提下，求解得到经济性更好的预防控制策略，证明了IDE-EELM算法优越的寻优能力和求解结果的有效性；

2)通过对IDE-EELM算法计算性能的分析，表明利用IDE-EELM算法求解TSPC模型可大幅度减少优化求解的计算时间。