非平衡设计对检验效能的影响*
2019-09-17王星杰汪玉风潘海燕丁元林安胜利
王星杰 汪玉风 潘海燕△ 丁元林 安胜利
【提 要】 目的 探究在完全随机设计的单因素方差分析中非平衡设计与检验效能大小的关系。方法 通过SAS程序分别估计出两类检验资料在给定参数下所需的样本总量,然后利用蒙特卡洛模拟固定样本总量时改变样本比得到的检验效能变化,以及样本总量不固定,改变各样本量时检验效能的变化。并且推断出在达到多大的样本比时检验效能低于预警值0.8。结果 在三组样本的单因素方差分析中,不固定样本总量时检验效能随样本总量增加或减少呈单调递增或递减。固定样本总量时检验效能与样本间的比例并不是呈简单的单调关系,而是受各样本均值与总均值之差平方和的影响。结论 三组样本的单因素方差分析中固定总样本量时,检验效能随样本间比值的变化呈不规则变化。在给定理论检验效能值的情况下能得出一个样本比临界值,在大于该值时检验效能值会低于0.8。
假设检验中,接受了实际不成立的H0(即Ⅱ类错误)时其概率为β,检验效能(power)也称把握度,其值为1-β,它的意义是当两总体确实有差别时,按规定的检验水准α所能发现该差别的能力[1]。样本量的估计是实验设计前的重要部分,过高或者过低的样本量都会影响实验的可靠性。理论检验效能是估计样本量的重要参数,为了使实验推测的结果足够可靠,我们一般在实验前先设定理论检验效能,并以此来算样本量[2]。影响检验效能的因素有四个,分别是:实验设计类型及方法、检验水准α、效应量以及样本量[3]。本次实验着重考虑实验设计方法和样本量对检验效能的影响。实验设计按样本量相等与否分为两类,当样本量相等时称为平衡设计,不相等时称为非平衡设计。一般的观点认为平衡设计时检验效能是最高的,本研究我们通过非平衡设计改变样本量之间的比值,然后利用蒙特卡洛模拟分析计算其检验效能,观察其变化,并结合公式进行解释。
模拟方法
Monte Carlo法又称随机模拟法,它是利用不同分布随机变量的抽样序列模拟实际系统的概率统计模型,进而给出问题数值解的渐进估计值。具体步骤,设计一个随机事件,使一个事件的概率与某一未知数有关,然后在软件中重复实验,利用这个事件出现的频率近似得出它的概率,求出未知数的近似值。如果要计算检验效能,可以将其定为未知数,先用正态分布模拟出各样本的数据,然后对其进行单因素方差分析。重复上述步骤1000次,统计出结果接受H0的频率。因为大样本所得的频率可以近似估计总体的频率,所以在已知H0不成立时得到的接受H0的频率,可以近似看作是本次假设检验在当前条件下的Ⅱ类错误的估计值。同理,模拟不同分布就可以得到其相应的检验效能估计值[4]。
在临床试验研究中,应保证实验达到一定的检验效能。当P>0.05时会产生“阴性结果”,人们往往认为此时的差别无统计学意义,实则忽视了这可能是由检验效能过低引起的,从而放过了本来可能有统计学意义的结果。所以一般情况下,尽管尚有争议,一些学者建议在得到阴性结果的同时应该注明其检验效能,这样可以使读者了解到更多的统计信息。通常规定检验效能应该不低于0.75或者0.80,这里我们选取0.80作为检验效能的警戒值[5]。
当前有很多软件都可以进行样本量的估计,如:SAS、SPSS、nQuery A dvisor和PASS等[6],还有一些网站也提供了样本量估计模块,如:http://powerandsamplesize.com/等。本次研究我们利用SAS 9.3中的proc power程序进行给定参数下的样本量估计。
模拟过程和结果
1.三组样本的单因素方差分析
单因素方差分析用到的基本公式,由Cohen提出:

2.固定样本总量
在固定总样本量的情况下各组样本间不同比例所对应的检验效能。分别增加第一组和第二组样本所占比例,检验效能都逐渐减小,且第二组样本比例变化所引起的检验效能降低幅度要大于第一组。以理论检验效能值0.9为例,增加第三组样本所占比例时,检验效能先逐渐增加,在样本比例达到1:1:4时检验效能低于0.90。同时增加二、三组样本所占比例,其检验效能降低。但同时增加一、三组所占比例,其检验效能逐渐增加,且增幅超过单独增加第三组比例时的增幅。当一、三组所占比例达到一定程度后,如20:1:20,检验效能开始降低,见表1。
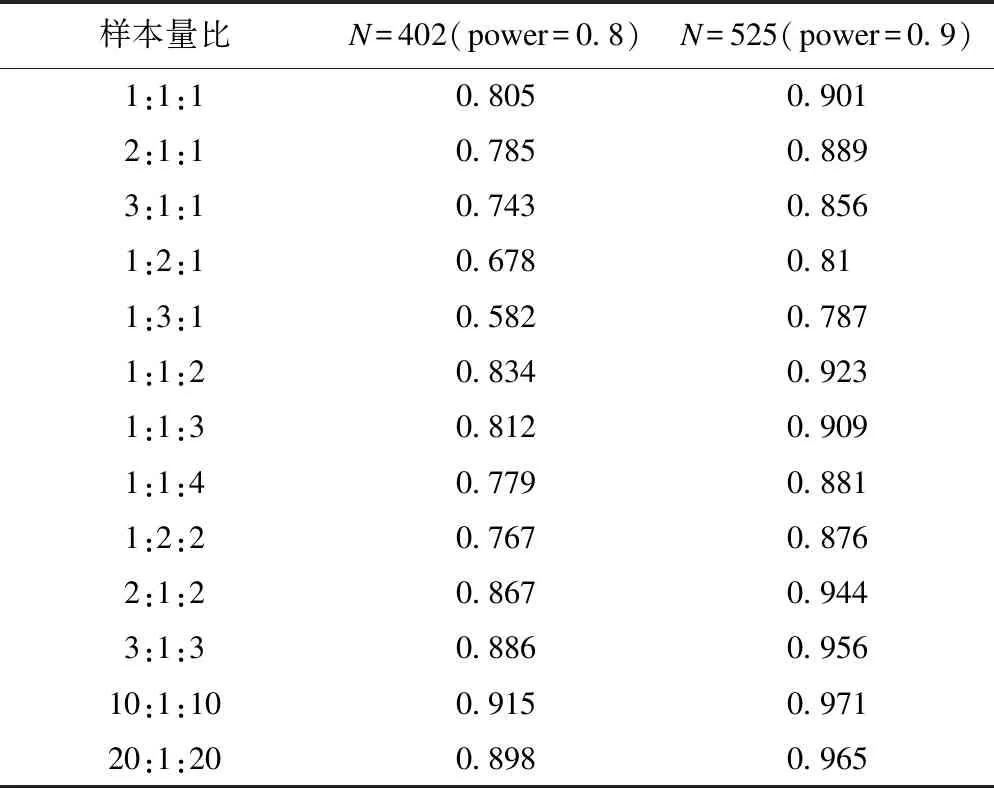
表1 固定样本总量改变样本量比所对应的检验效能(power)值
*:N=样本总量
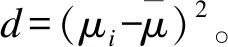
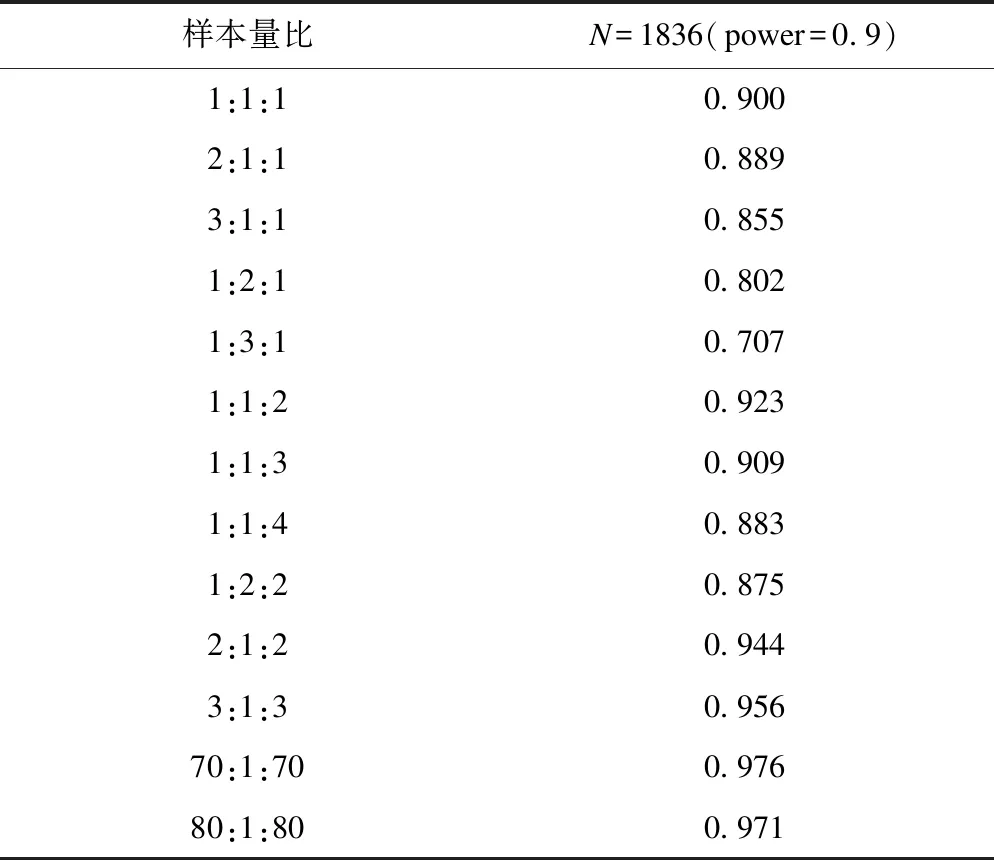
表2 固定样本总量改变样本量比所对应的检验效能(power)值
*:N=样本总量
从表2中我们可以看出其结果与上述结论一致,在最大d值所对应的第三组样本达到1:1:3时检验效能开始降低,所以应将比例维持在1:1:3以内。在最小d值所对应的第二组样本达到1:3:1时检验效能小于0.8(这是理论检验效能在0.9时得出的结论,同理可以得出不同理论检验效能下的临界比例)。唯一不同的是当一、三组所占比例增加到更高时检验效能才开始降低。我们可以得出当样本总量增加时,三组样本间需要更大的比例才会使样本严重失衡,所以使样本严重失衡的比例并不是固定的。
3.样本量不固定
各样本量同时增加或减少时,检验效能随总样本量的变化,见图1。在各样本量相等,同时增大或减小相同值的情况下,检验效能随着样本量的增加而增加,且增长趋势逐渐变缓。接下来探究总样本量不固定,单独增加某些样本的样本量时检验效能的变化。以大样本量1836为例。各组样本量相等时为612,这时的理论检验效能为0.90,见表3。
由表3可以看出单独增加第一组样本量时,其检验效能随样本量的增加而增加,单独减少第一组样本量时其检验效能随样本量的减少而降低(第二、三组同理)。单独增加第二组样本量时其检验效能的增幅很小(出现两个0.901可能是因为四舍五入造成的)几乎不变。同时减少三组样本时其检验效能随之降低(增加同理)。原因同上,是受d值大小的影响。

图1 检验效能随总样本量的变化

各组样本量power值(620,612,612)0.902(650,612,612)0.907(700,612,612)0.915(612,620,612)0.901(612,650,612)0.901(612,700,612)0.902(600,612,612)0.898(600,600,600)0.894
结 论
当样本总量固定,分析三组样本时并不是各组样本量相同其检验效能就最大,所以我们可以适当减少d值较小组的样本量,增加d值较大组的样本量,且最好是同时增加两组d值较大的样本量,这样得到的检验效能会大于单独增加d值最高组的样本量。同时也要注意不可使样本间差距过大导致样本严重失衡。如:当增加d值最大组样本量时比例应维持在1:1:3以内。当样本总量不固定我们可以通过增加d值较大组的样本量来增加检验效能。如果出于成本、时间等考虑要减少样本量时,可以优先减少d值较小组的样本量,使其对检验效能的影响降到最低。
本研究结论不同于研究者的惯性思维(即检验效能随着样本量的增加而增大),提醒我们在设计各组样本量时,不能仅凭经验进行判断,而是应该建立在合理的统计推断结论之下。此次研究只针对三样本资料进行了论述,具有一定的局限性,目前有关这方面的研究文献较少,多样本资料的相关分析还有待进一步补充和完善。
