基于因子分析法的中小机场空管安全水平定量评估

2019-09-17民航西南地区空中交通管理局李建光

民航管理 2019年8期

□ 民航西南地区空中交通管理局李建光/文

安全空管是空管发展的基础和前提。随着民航业的迅速发展，空管单位的安全保障能力是否能与航班量增长相匹配，安全水平能否满足预期要求，已经成为业界和社会关注的热点。中小机场运行环境复杂、局方监管难度较大。近年来，中小机场的空管安全事件频发。统计数据表明，造成这种现象的原因是多方面的，既有人员因素（比如部分管制员业务能力不足），也有非人员因素（比如设备故障、组织管理弱）。

为对中小机场空管运行安全水平实现有效监控，必须开展综合评价。以往的空管安全保障能力评估多为定性评估，定量评估较少，且针对中小机场的空管安全评估研究更少。民航局颁布的《民航空中交通管理安全评估管理办法（AP-83-TM-2011-01）》和《民用航空空中交通管理运行单位安全管理规则（CCAR-83）》明确指出，民航空管运行单位应当建立安全评估机制，但是，对于空管单位安全能力评估指标体系构建及方法未给出具体方案。有学者从人机环管四个方面基于结构方程模型来验证筛选安全风险主导因子。李远构建了空管单位安全能力定量评估指标体系，并采取G 1-TOPSIS方法开展量化评估。在现阶段，针对中小机场的空管安全保障能力评估需要进一步设计科学合理的量化评估手段，并可从指标体系构建、评价模型设计、量化结果分析等方面来展开。本文将基于因子分析法开展中小机场空管安全保障能力量化评估。

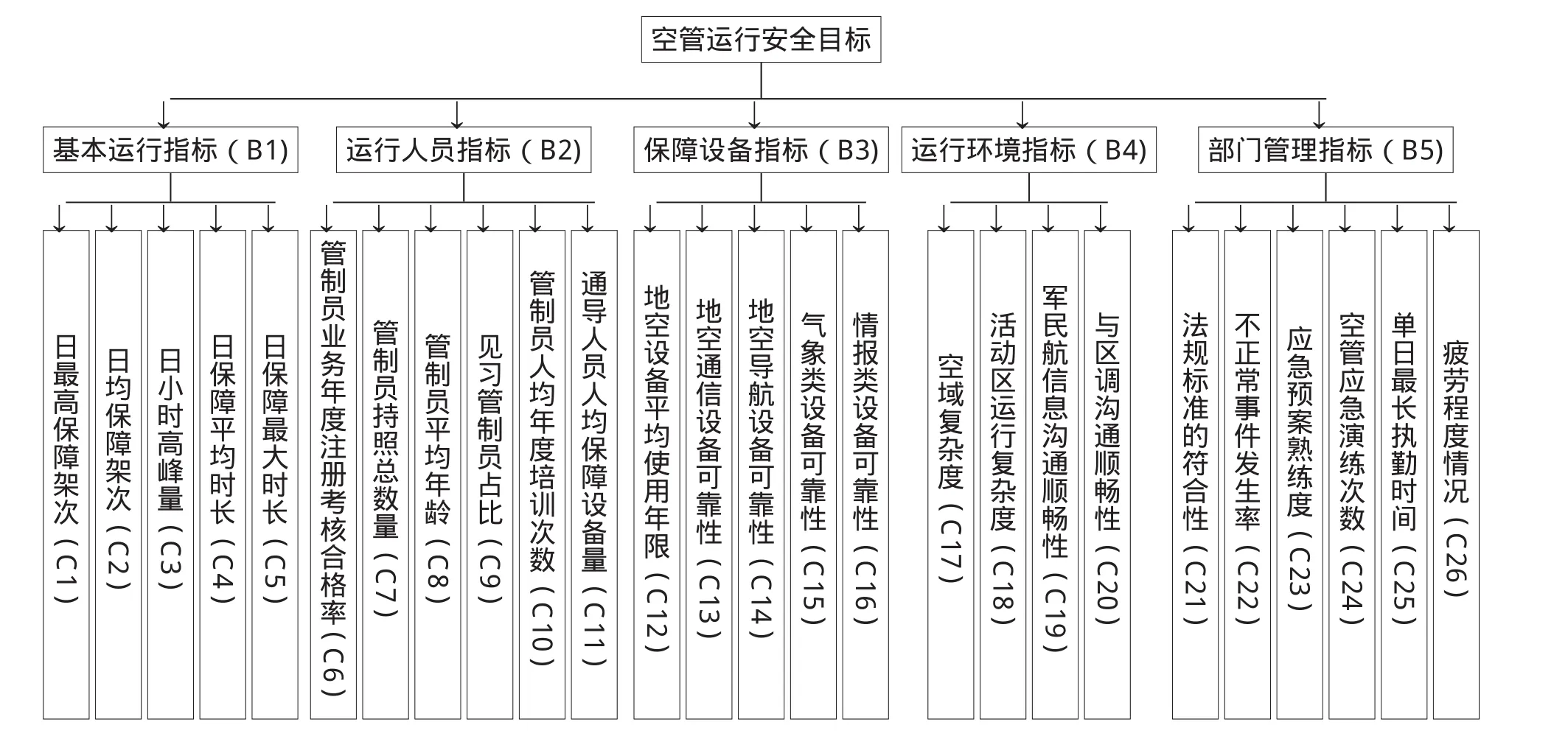
图1：中小机场空管运行安全水平评估指标体系

基本思路

从建立评估指标体系、构建评估模型和评估模型应用三个阶段来展开中小机场空管安全水平综合评价。首先，建立中小机场空管运行单位安全水平评估指标体系。在空管运行单位实地调研和数据采集的基础上，综合专家意见，筛选有效的评估指标因子并对指标在空管运行中的具体表现做详细定义或描述。然后，构建空管运行单位安全水平评估模型。结合空管运行实际，对空管运行安全水平评估方法进行研究，尤其是方法的可行性分析，所选安全评估方法应能与设置的评估指标体系有效衔接，以期构建的综合评估模型既能够实现对指标体系数据利用的完备性，又能计算出科学合理的安全水平分值。最后，对所选择的安全水平评估模型结合中小机场空管运行实际展开安全评估应用。

中小机场空管安全水平评估体系

（一）评估指标体系的构建

首先建立中小机场空管安全评价指标体系。空中交通系统组成元素众多、关系复杂、安全性要求非常高。主要考虑空管单位安全水平有关的基础运行、人员、保障设备、运行环境和部门管理五个方面来构建评估指标体系，如图1所示。

（二）评估思路

在建立综合评价指标体系的基础上，采取因子分析法来进行量化评估。因子分析法是将多个实测变量转换为少数几个不相关的综合指标的多元统计方法，也就设计出多个观测变量，从多个变量收集大量数据以便进行分析寻找规律。这样既可减轻收集信息的工作量，且各综合指标代表的信息不重叠。

基于因子分析的中小机场空管安全水平评估模型

设p个可观测的指标为X1，X2，…，Xp，m个不可观测的因子为F1，F2，…，Fm。一般情况下，公共因子不可能包含总体的所有信息，每个观测变量除了可以由公共因子解释的部分外，还会有一些其他解释不了的部分，称之为相应变量的特殊因子。

（一）因子分析模型的一般形式

因子分析模型的一般形式记为

其中，m≤p，F1，F2，…，Fm为初始变量的公共因子，εi为变量Xi的特殊因子。如果是正交的因子模型，还进一步要求公共因子是互不相关的，特殊因子和公共因子也不相关。记

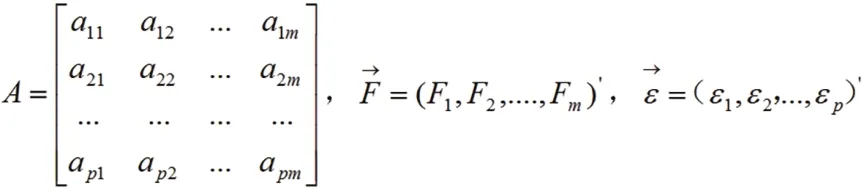
（二）载荷矩阵的估计

要建立实际问题的因子模型，关键要根据样本数据估计因子载荷矩阵A。对A的估计方法很多，现使用较为普遍的主成份方法，由于它的估计结果和初始变量的主成分仅相差一个常数倍，故称为主成分法。除此之外，常用的方法还有最大似然法，α因子分析法、加权最小二乘法、映像因子分析法和最小残差法等。

（三）因子旋转

因子旋转的依据是因子模型的不惟一性。设T是一个正交矩阵，由于TT‘＝E，所以因子模型与等价，而后者的载荷矩阵为B＝AT，公共因子为

因子旋转的目的要使初始因子载荷阵A经一系列旋转后结构简化，即达到以下原则：①每个公共因子只在少数几个测试变量上具有高负荷，其余负荷很小或至多中等大。②每个测试变量仅在一个公共因子上有较大负荷，而在其余公共因子上的负荷较小或至多是中等大小。

可见，旋转的目的是使每一个测试矢量在新的坐标轴上的射影尽可能向1和0两极分化。对因子负荷阵旋转的方法有多种，如正交旋转，斜交旋转等，常用方法为方差最大化正交旋转(Varimax)。

（四）因子得分函数的估计

在所建立的因子模型中，已将总体中的原有变量分解为公共因子与特殊因子的线性组合

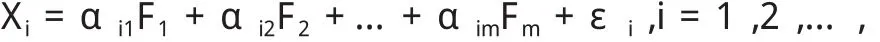
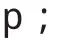
表1：某中小机场空管运行安全评价指标汇总

表1：某中小机场空管运行安全评价指标汇总（续）

表2：变量共同度

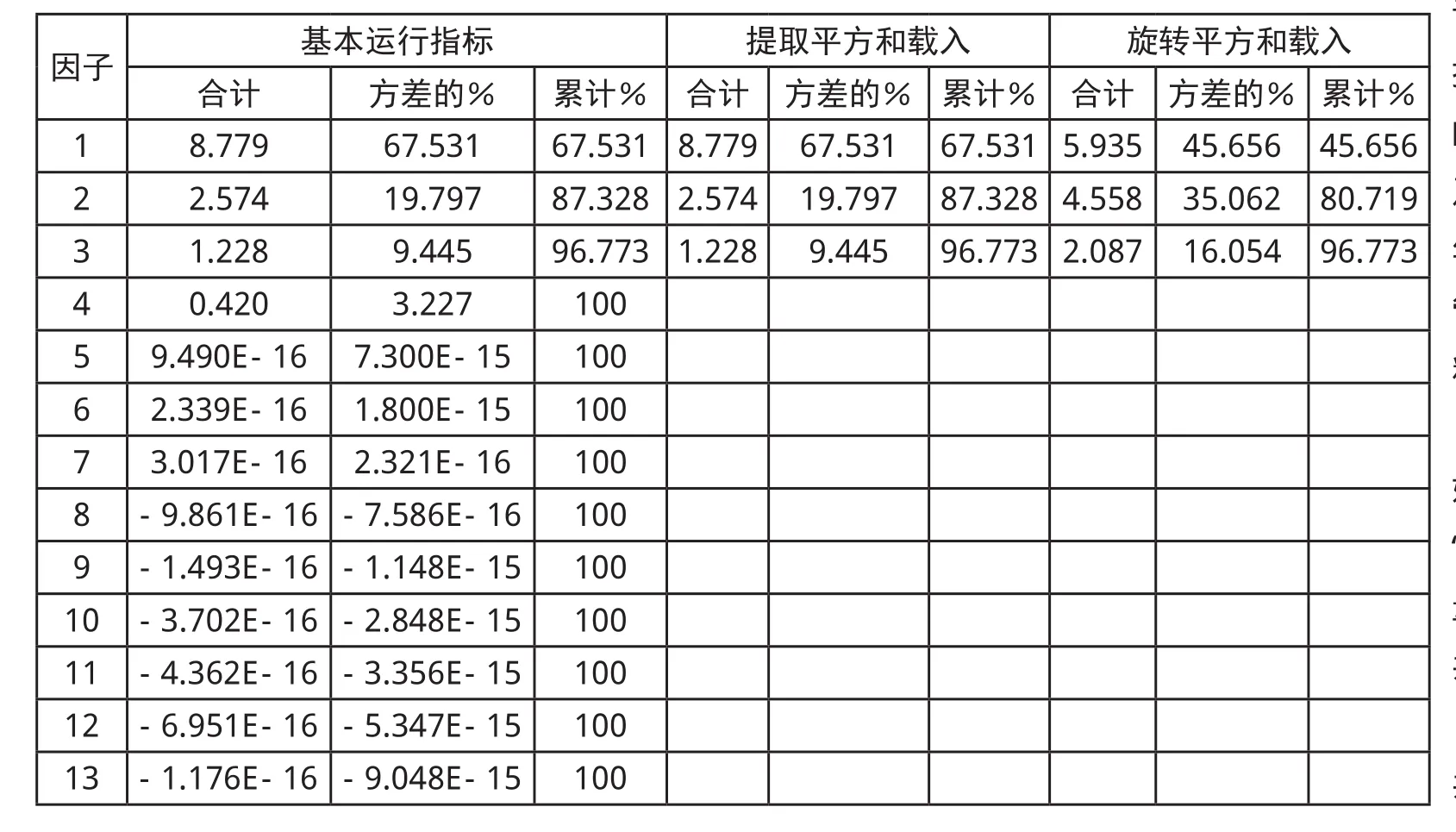
表3：方差及其累积和

同样地，可以把每个公共因子表示成原有变量的线性组合

Fi＝γj1F1＋γj2F2＋…＋γjpXp，j＝1，2，…，m；称之为因子得分函数，用它可以计算每个观测记录在各公共因子上的得分，从而解决公共因子不可预测的问题，获得因子得分函数的关键是求解估计参数，常用的估计方法有Thompson方法等。

（五）结果分析和应用

提取出反应原始观测变量特征的公共因子，并对其实施适当的因子旋转后，就需要对公因子加以解释，赋予其实际意义。对因子的解释是否恰当，不仅与数据本身的性质有关，还与研究者对专业知识的掌握及因子分析技巧的掌握程度有关。

某机场空管安全保障能力评估实例

以西南某中小机场为例，对其开展空管安全保障能力评估。通过现场调研、专家咨询等途径来进行数据的收集。所涉及的相关统计数据涉及2013至2017年。该中小机场空管运行安全基本资料见表1。

表2给出了初始变量的共同度。“提取”列表示变量共同度的取值，共同度取值区间为［0，1］。变量共同度反映每个变量对所提取出的所有公共因子的依赖程度。从表2可见，所提取的相关变量的共同度基本都在90%以上，说明提取的因子包含了原始变量的大部分信息，因子提取的效果比较理想。

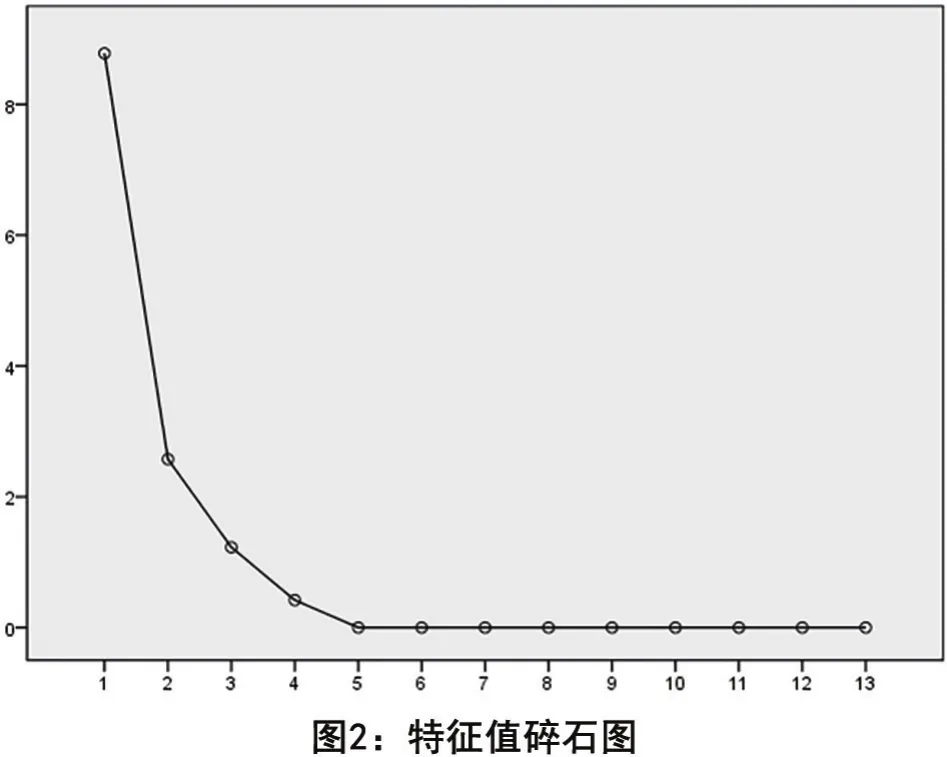
表3给出了每个公因子所解释的方差及其累积和。前3个公因子解释的累计方差己经达到96.773%以上，故提取这3个公因子就能够比较好地解释原有变量所包含的信息。图2为关于初始特征值（也就是方差贡献）的碎石图。观察发现，第3个公因子后的特征值变化趋缓，因而选3个公因子是比较恰当的。

表4和表5分别为旋转前后的因子矩阵。对比可以发现，表5中，旋转后每个公因子上的荷载分配更清晰了，因而比未旋转时更容易解释各因子的意义。

在确定模型提取出三个公因子后，对各公因子进行命名。表5中第1个公因子更能代表C 1日最高保障架次、C 2日均保障架次、C 4日保障平均时长、C 12地空设备平均使用年限、C 26疲劳程度情况。这五个指标主要表现空管保障需求情况，对于该机场空管运行安全水平评价来说，将其命名为“空管保障需求因子”。

第2个公因子更能代表C 5日保障最大时长、C 7管制员持照总数量、C 22不正常数量、C 24应急演练次数、C 25单日最长执勤时间。这五个指标主要表现机场空管保障应急处置能力状况，将其命名为“空管应急保障供给因子”。

第3个公共因子更能代表C 3日小时高峰量、C 8管制员平均年龄、C 9见习管制员占比。这三个指标主要表现空管保障的管制员队伍保障能力状况，对于该机场空管运行安全水平评价来说，将其命名为“空管人员能效因子”。

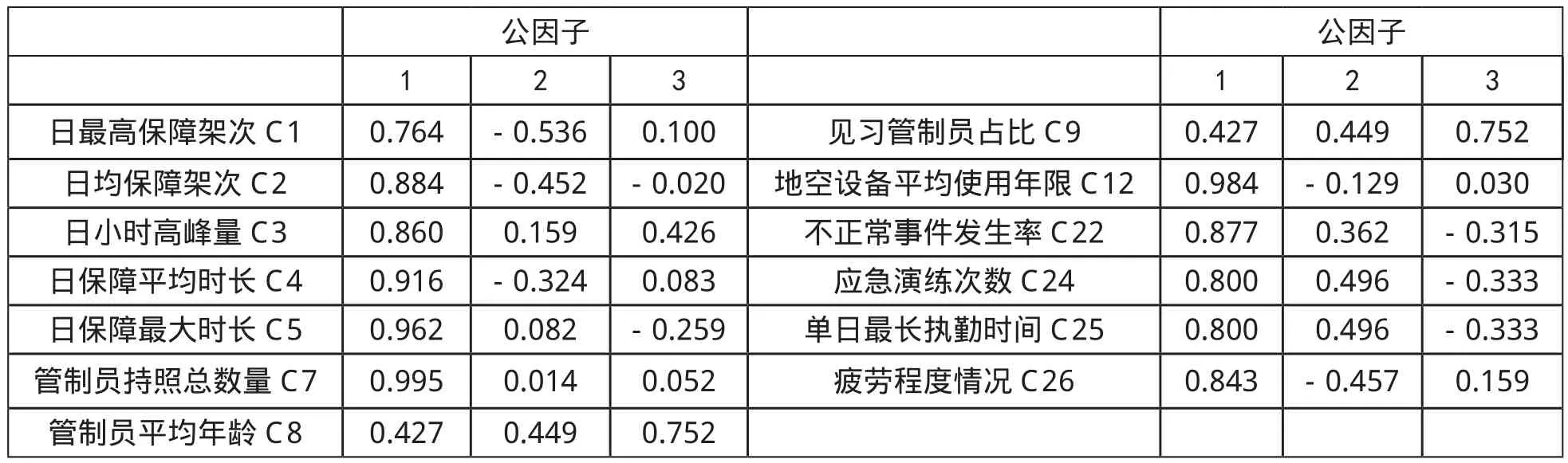
表4：因子矩阵

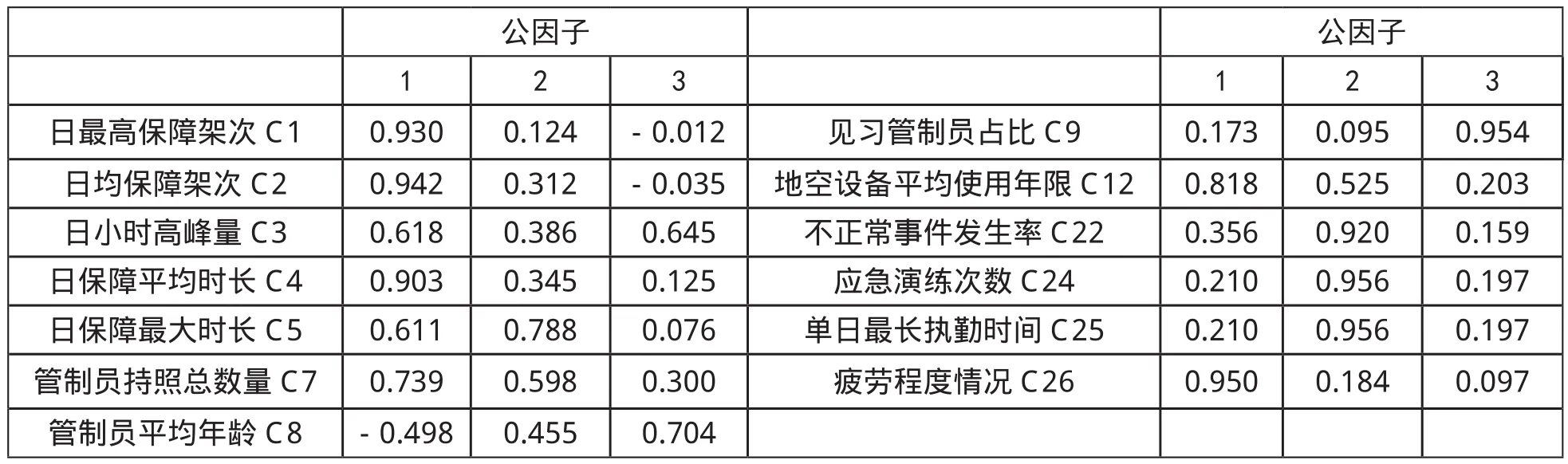
表5：旋转因子矩阵

进一步地，利用SPSS软件，得到三个公因子的得分计算函数为

为综合评价每一年机场空管运行安全水平，可对3个公共因子的得分进行加权求和，权数就取其方差贡献值或方差贡献率。结合表3可得该机场空管运行安全水平评价模型，计算公式如下：

z F＝45.656/96.773*公因子1（空管保障需求因子得分）＋35.062/96.773*公因子2（空管保障供给因子得分）＋16.054/96.773*公因子3（空管人员能效因子得分），得出各年份的该机场空管运行安全水平综合评价如表6所示。

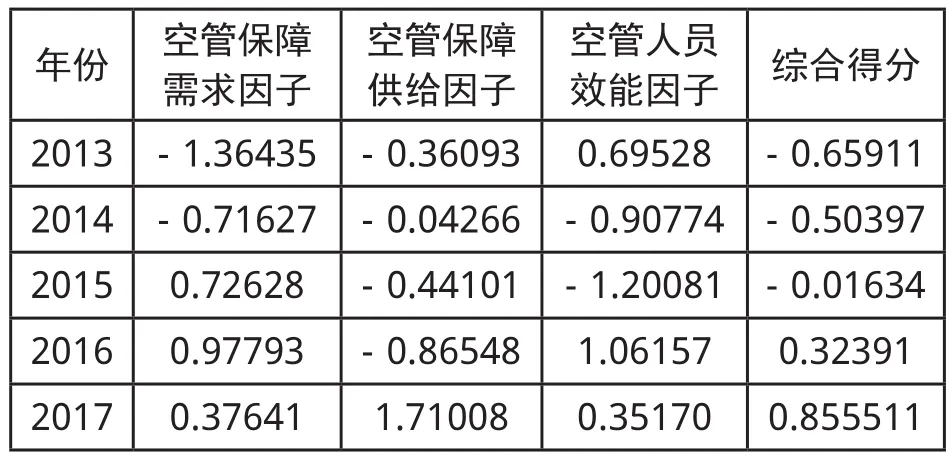
表6：2013年至2017年该机场空管运行水平综合评价得分

可见，从2013年至2017年，该机场空管运行安全水平逐步在提高。从表6可见，空管保障需求因子和空管保障供给因子的两个方差贡献率差不多，但是从2015年开始，两个因子的得分差距开始逐渐增加，到2017年，两个因子的得分差距呈减小趋势，说明该机场空管运行能力向好处发展，尤其是在2017年，随着空管保障供给因子得分的提升，该机场整体空管运行安全能力提升较快。对“空管保障供给因子”而言，从表5旋转因子矩阵可知，C 5日保障最大时长、C 7管制员持照总数量、C 22不正常数量、C 24应急演练次数、C 25单日最长执勤时间的载荷因子相对较大，也即影响较大。因此，建议该机场空管部门在日保障时长增加的趋势下，应扩大持照管制员队伍规模，并同步加快管制员的应急处置能力培养，提高空管运行保障安全水平。

空管人员能效因子中C 3日小时高峰量、C 8管制员平均年龄、C 9见习管制员占比所占的载荷较大，而空管人员能效因子在表6“2013年至2017年该机场空管运行水平综合评价得分”中，因子得分低于0的年份有2014年和2015年，其余年份均大于0，这说明，该机场空管部门的管制人员队伍年龄构成、见习管制员数量两方面的工作控制在近年来比较有成效。