基于BP 神经网络防空反导指控网络抗毁性评估*

姜浩博，李 松，林 驰，吕元杰，张 杰

（1.空军工程大学研究生院，西安 710051；2.空军工程大学防空反导学院，西安 710051）

0 引言

抗毁性的定义来源于民用网络，它描述了某些因素使得网络引发故障时，网络可以利用某些手段来减少受到的伤害并恢复至原有能力的能力［1-7］。军事领域中，随着现代战争的快速发展，战争速度越来越快，战争方式越来越多样化，提高自己在战场上的生存能力才能掌握战斗的主动权，所以抗毁性的意义更是可想而知。在军事领域，指控网络抗毁性被越来越多的人关注。见文献［8-14］。

目前对于网络抗毁性的研究，局限于对抗毁性某一方面进行分析，缺少对指控网络抗毁性整体进行评价的方法。本文通过对防空反导指控网络抗毁性进行分析，得到了评价其抗毁性的关键要素，建立评估指标体系，通过专家打分作为样本，对分数进行量化，由于BP 神经网络具有非线性映射能力和自适应自学习能力，利用BP 神经网络针对防空反导指控网络抗毁性建立评估模型，通过比较选出最优模型，通过仿真得出权重，最后将几种方法进行对比分析，最终证实该模型的有效性。

1 防空反导指控系统的作战特点分析

防空反导指控系统是指用于收集、处理、显示空中情报，进行威胁判断，目标参数和设计诸元计算，火力分配和辅助决策，并对防空反导武器系统实施指挥控制的人机交互系统，也是防空反导作战的核心。结合防空和反导的作战方式，归结出以下特点。

1.1 高精度、高可靠性、强实时性

众所周知，只有比进攻的精度要求高，才能有效地阻止敌方的进攻。在防空反导作战中，对抗目标具有目标特点繁杂、种类多样，进攻手段丰富，处理的信息量庞大，涉及层面多，作战空域广等特点，这就使得防空反导作战拦截难度大大增加。此外，由于反导作战的特点，使得战斗节奏越来越快，环环相扣。一次小的误差、延迟或者失误，都可能使得战机延误，导致最终的拦截失败。同时，还要兼顾防空作战。因此，在这样一个高强度、高复杂、高冲突的情况下，指挥控制系统的高精度、高可靠性是确保成功拦截的关键，而强实时性是实施拦截的基础。

1.2 高效的信息流传输、处理能力和指挥控制系统的高度自动化、智能化

由于防空反导作战对象作战能力的日益提高（如突然、高速、小RCS、大入射角、飞行时间短以及技术日益提高和突防措施的采用等特点）、目标类型的繁杂，对抗目标的发现、识别、拦截等战机稍纵即逝，这些特点使得指挥控制系统必须要具有高效、高质量的信息传输和信息处理能力，只有高度自动化和智能化的指挥控制系统，才可以加快信息处理的速度，辅助决策等使得作战反应时间大大缩短。

1.3 高度一体化

防空反导一体化作战指挥控制系统要在强对抗、强实时、高自动化、高智能、资源高度冲突等复杂条件下，对多种、多型作战资源的空域、时域、模式、体制等的作战使用，进行优化协同、智能决策、实时反馈控制。相对于传统的作战指挥、控制，更加强调智能、交链、协同、一体，力求对作战资源在体系、系统、平台的各个层面进行实时任务规划和优化，并通过深层次的交链控制，实现一体化，有效减小作战平台及其相关资源的使用对指挥员、操作员的依赖性，提高了作战效率。

从上述特点可知，防空反导作战的基础就应该是指控网络的抗毁，抗毁是作战的前提，这就使得防空反导指控网络的抗毁性研究已经成为不可缺少的一项工作。

2 BP 神经网络的算法流程

BP 神经网络也称为误差反向传播网络（Error Back-Propagation Network），是由Rumelhant 等人在1985 年提出，是目前最具有代表性，使用最广泛的人工神经网络模型。BP 神经网络实质上就是一种输入到输出的映射，它不需要精确的数学表达式作支撑，只需要输入数据和输出数据，在输入输出之间构建一个BP 神经网络，使得该网络在输入数据之后得到想要的输出结果［15-16］。BP 神经网络结构包括输入层（input）、隐含层（hide layer）和输出层（output layer），如图1 所示。

图1 BP 神经网络结构

BP 神经网络算法步骤如下：

第1 步：对权值初始化。

第2 步：给出M 个训练样本。

第3 步：把给出的训练样本放进网络。

第4 步：计算出隐含层和输出层的各单元输出。

其中，（p）代表第p 个样本输入后的情况，xbi为第i层第b 个输入值，yai为第i 层第a 个节点输出值，Ni-1为第i-1 层节点的个数，bai为第i 层第a 个节点的阈值，fai（·）是第i 层第a 个节点的激活函数，Ni表示第i 层的节点个数，l 表示BP 神经网络总层数。a 取1 到Ni之间的整数，i 取1 到l 之间的整数，p 取l 到M 之间的整数。

第5 步：求平方误差。

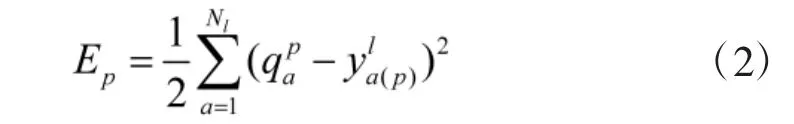
其中，EP为第p 个样本的平方误差，qap是第p 个样本输入到网络后得到的第a 个节点的输出值的期望，yla（p）是第p 个样本输入到网络后得到的第a 个节点的输出值。

第6 步：判断误差是否满足要求。如果不满足则继续第7 步，如果满足则调至第9 步。

第7 步：通过误差来确定权值改变量。

第8 步：调整权值ωab（m），并返回第4 步。

其中，ωab（m）为第m 次循环的次数，E 为当前平方误差，η 为学习效率。

第9 步：判断所有的误差是否都满足要求。如果不满足则返回第7 步，如果满足则结束学习。

3 抗毁性评估过程

通过对评价过程的学习和对指控网络抗毁性评估的了解，绘制出指控网络抗毁性评估流程图如图2 所示。

图2 指控网络抗毁性评估流程图

3.1 抗毁性评估指标体系的建立

随着信息化的发展，现代化战争已经不再是以前的单一作战方式，而越来越强调体系。在防空反导指挥控制系统中，将单个装备集成到网络中，每一台装备都能通过网络进行信息共享，获得实时的战场情况，作出自己的决策。可以将系统中的每一台装备都抽象成一个节点，装备之间传递的信息流抽象为边，这样防空反导指挥控制系统就可以抽象为一个网络［17］。而指控网络不是简单的通信网络，而是一种具有指控能力和通信能力的网络。对于防空反导指挥控制网络而言，抗毁性的含义就是防空反导指挥控制网络受到打击之后，或规定时间内仍可以完成任务的能力。因此，将防空反导指挥控制网络的抗毁性分为以下3 个方面进行分析。

3.1.1 网络结构特点

是指网络拓扑结构自身所拥有的某些特征属性。包括以下指标：网络凝聚度和网络稳定性。网络凝聚度是以当加权网络退化到无权网络的时候的平均最短距离为基础，对整个网络的凝聚情况的评价。网络稳定性是对网络是否稳定进行评价。

3.1.2 网络抗毁能力

是指整个网络拓扑结构发生变化而不影响其功能，或者受到外界打击而没有发生结构变化的能力。包括以下指标：指控关系改变能力、网络恢复能力和网络连通能力。指控关系改变能力指当网络中指控关系发生变化，整个网络的影响能力；网络稳定性是指网络受到打击之后避免损伤的能力。网络恢复能力是指网络在受到打击后，在规定的时间内仍可以完成任务的能力。网络连通能力是指当网络中减少节点而不影响整个网络性能的能力。

3.1.3 节点抗毁能力

节点抗毁能力是指节点在受到打击之后在规定时间内仍能完成规定任务的能力。节点抗毁能力分为以下几个指标：节点恢复能力、节点抗打击能力和节点协作能力。节点恢复能力是指节点受到打击之后，能力不是立刻消失，而是一种动态缓慢失效或恢复，并可以在规定时间内完成任务的能力［13］。节点抗打击能力是指节点受到打击后没有受到任何影响的能力。节点协作能力是指网络中不同属性节点之间互相帮助的能力。

通过以上分析可得到如图3 所示的防空反导指控网络抗毁性评估指标体系。

图3 防空反导指控网络抗毁性评估指标体系

3.2 指标量化及数据获取

对防空反导指控网络抗毁性指标进行评价属于主观评价，而主观评价很大程度上具有模糊性，需要对其模糊评价进行量化。本文中将主观评价分为4 个等级，从高到低依次为优、良、中、差。本文中将指标量化为x，并认为x 服从正态分布N（0，1），设差、中、良、优的量化值分别为x1、x2、x3、x4，评价为差、中、良、优的次数分别为a1、a2、a3、a4。在x 的正态分布的横坐标轴上，将其分为4 部分，用yi表示分割点，yi可用以下公式求得：

其中，Pi为前i 个等级的次数概率之和。i 取值为1到3。这样每个指标等级就可以对应其相应的取值区间。选择其中位数来对指标的等级进行量化：

其中，j 取1 到4。通过查询正态分布表可以得出x1、x2、x3、x4的值，其对应的就是差、中、良、优的“标准分”成绩［18］。

本文中邀请了50 位防空反导专家对不同的网络进行评估，其对各个指标进行评估，选取10 个具有代表性的结果。如表1 所示，按照之前在前面所述的方法将这些评价结果进行量化，量化后的值如下页表2 所示。

3.3 建立BP 神经网络模型

3.3.1 输入层、隐含层、输出层的设计

此次试验中，选用输入层节点数为8，输出层节点数为1，隐含层层数为1，隐含层节点数用经验公式选出：

其中，h 为隐含层节点数，i 为输入层节点数，o 为输出层节点数，a 为1～10 之间常数，所以在本次实验中隐含层神经元个数的选择范围为3～13。

3.3.2 传递函数的确定

BP 神经网络传递函数种类很多，通过验证可以发现如果传递函数使用tansig 函数，误差要比logsig 函数小，所以选用tansig 函数作为隐含层传递函数。输出层传递函数采用线性传递函数purelin函数。

3.3.3 权值的初始化确定

在本次试验中，将初始权值取为0～1 之间的随机数。

3.3.4 学习速率、期望误差、训练最大次数的选取

学习速率一般选取0.01～0.8 之间的数，本次实验选取学习速率为0.2，期望误差为10-5，训练最大次数为10 000 次。

3.3.5 训练方法的选择

表1 专家评价结果

采用基于数值优化的3 种改进方法进行比较。它们分别是梯度下降法、拟牛顿法和Levenberg-Marquardt（LM）算法。

表2 评价量化结果

4 仿真及对比

4.1 神经网络的确定和训练

本文用MATLAB 对其进行仿真研究。通过对不同的神经网络训练方法和不同的隐含层神经元个数，分别进行神经网络的训练，通过对训练误差来选择合适的训练方法和隐含层神经元个数，训练结果如表3 所示。

表3 不同训练方法和隐含层神经元个数的误差比较

通过比较可以发现，当选用Levenberg-Marquardt 算法和隐含层神经元个数为6 时误差最小，所以在后面的仿真中选用这个组合。经过训练后得出的网络如图4 所示。

图4 训练结果示意图

4.2 权值分析

建立好的神经网络模型，利用net.iw、net.lw 和net.b 函数对其权值和阈值进行调用，结果如表4所示。

表4 神经网络每层的权值和阈值

利用Garson 提出的利用神经网络每层权值来计算输入量对输出量之间权重的方法［19］，公式如下：

最后通过式（9）可以计算出各个输入量对输出量的权重如图5 所示。

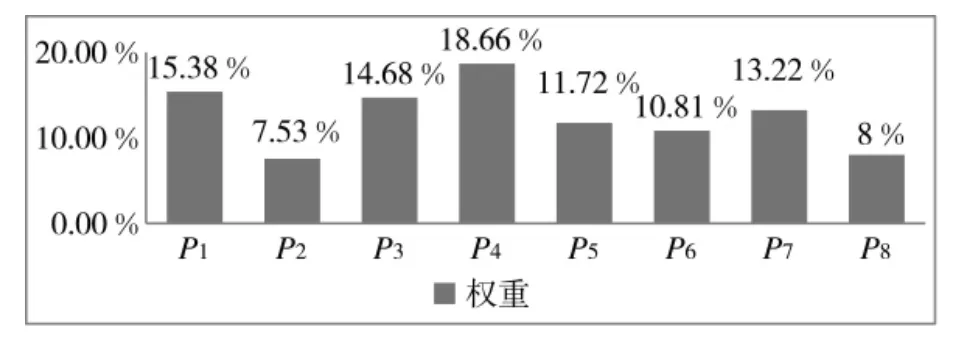
图5 输入量对输出量的权值

4.3 对比分析

另请10 名防空反导专家对指挥控制网络进行评估，分别用BP 神经网络中的梯度下降法、拟牛顿算法、Levenberg-Marquardt 算法3 种算法和AHP 层次分析法，对防空反导指控网络评估建模，对这4 种评估模型进行验证，最终正确率结果如表5 所示。

表5 验证4 种方法的正确率

通过以上结果证实了基于Levenberg-Marquardt算法的BP 神经网络模型，对防空反导指控网络评估更具有可行性。

5 结论

本文通过对防空反导指挥控制网络的抗毁性分析，在专家进行主观打分的基础上，利用BP 神经网络具有的非线性映射能力和自适应自学习能力，很好地解决了网络的抗毁性要素权重确定的问题，并对训练出来的网络进行对比检验，检验结果证明了网络的可行性。对以后的指挥控制网络抗毁性评估有着一定的指导意义。