基于量子蚁群算法的VRPTW 研究*

徐廷学，张海军，付霖宇，刘崇屹

（海军航空大学，山东 烟台 264001）

0 引言

配送车辆的路径问题（Vehicle Routing Problem，VRP）是Dantzig 和Ramser［1］在1959 年提出来的。所谓VRP，一般指的是：调用多辆车辆，从车场出发，对客户组织适当的行车路线，有序地访问所有客户并且只访问一次，在满足所有设定的约束条件下，力争实现所设定的目标。

带时间窗约束的车辆路径问题（VRPTW）是车辆路径问题（VRP）的基拓展与延伸，广泛应用于资源配置和物流运输等方面。求解VRPTW 的算法大致可以分为精确算法和启发式算法两类［2-3］。精确算法（Accurately Arithmetic）在求解规模较小的路径优化问题时，能够在可承受的空间与时间消耗下得到精确解。但是配送路径优化问题属于NP 问题，实际求解过程中问题的规模较大，使用精确算法所消耗的空间和时间成本都是比较大的。而启发式算法（Heuristics）不管是求解小规模的问题还是大规模的问题，都能够在一定的范围和较短的时间内给出满意解或最优解。因此，目前相关领域的专家以及研究人员，对于求解算法的主要研究方向是启发式算法，特别是对现代启发式算法的研究。

蚁群算法作为现代启发式算法之一，自从被提出之后就受到了广泛的关注，该算法具有正反馈性、并行性和鲁棒性等优点，在解决任务分配、路径优化等问题时表现出了良好的性能，但同时蚁群算法也存在一定的缺陷，如在解决大规模的问题时，会出现运算时间长、收敛速度慢、容易陷入局部最优解等问题［4］。本文在基本蚁群算法的基础上进行合理改进，将量子计算的理念与方法融入蚁群算法，提高了算法的性能，首先，改进后的算法更加科学地初始化蚂蚁的位置，使蚂蚁有更大可能性地寻找到最优路径。然后，在搜索的过程中添加量子比特启发式因子，同时，使用局部信息素更新和全局信息素更新相结合的信息素更新方式，并且全局信息素更新添加了量子旋转门的新模式。最后使用2-opt 搜索对结果进行进一步地探索，扩大搜索的范围，增加了得到最优解的概率。使新建立的量子蚁群算法能够实现对模型更加高效的求解。

1 问题描述及数学建模

1.1 偏离时间约束时的惩罚函数

在VRPTW 中目标函数注重的成分，除了行驶路程的长短以及消耗时间的多少之外，更为注重限定时间的约束，前者带来的是配送车辆行进产生的成本消耗，而后者带来的是违反限定时间之后造成的惩罚花费，通常来讲，后者尤为重要。当从配送中心出发的配送车辆没有按照限定时间将物资送达客户手中时，就会产生惩罚花费，而车辆抵达的时间和限定时间相差越大，那么产生的代价就越大。惩罚的代价会随着时间差的增大而呈现线性或者是指数等变化［5］，这种变化是由现实中的状态而决定的。

在VRPTW 的模型建立中，会将惩罚函数作为其中的约束之一，这里要对模型中的惩罚函数作出合理规化。作出的惩罚函数如下：

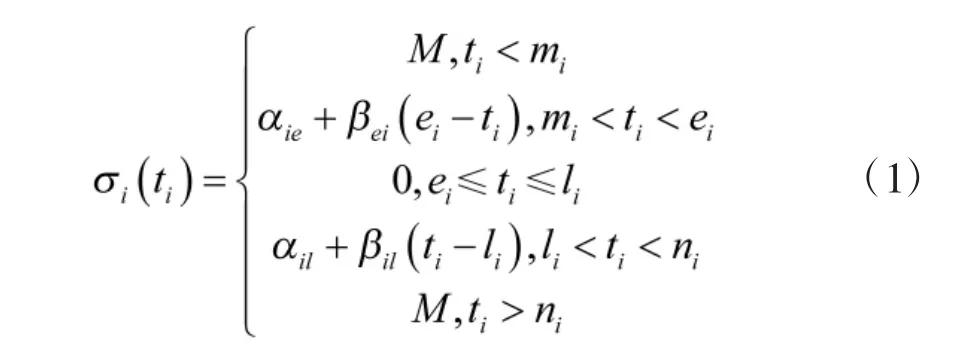
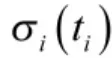
式（1）惩罚函数如图1 所示。

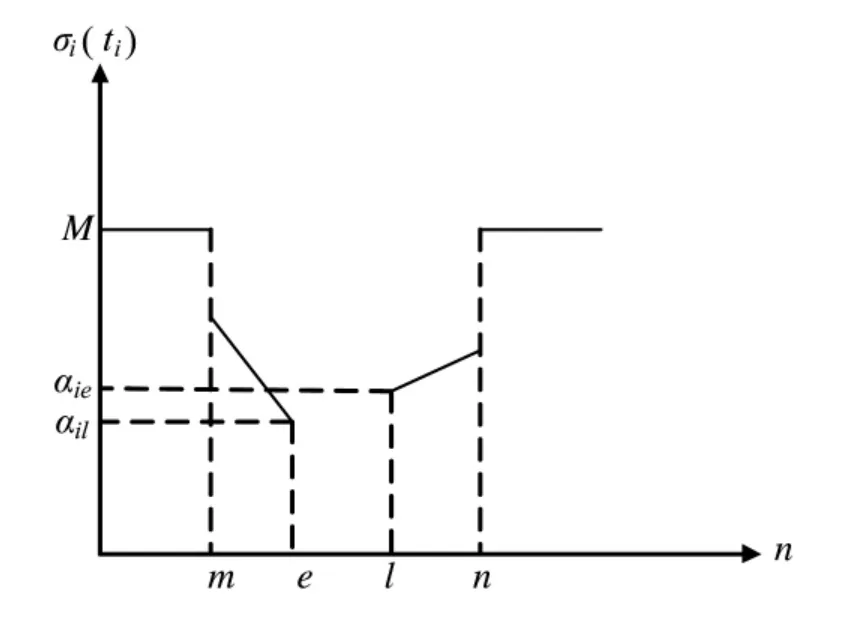
图1 VRPTW 模型中惩罚函数

1.2 VRPTW 模型的建立

VRPTW 是从同一车场出发的多辆车辆按照约定好的时间访问多个客户进行运送货物的问题。已知出发车场的位置以及需要访问的客户的位置，客户的数量以及需求数量，客户约定好的时间段，车辆的数量以及负载数量，对客户组织适当的行车路线，有序地访问所有客户并且只访问一次，在满足所有设定的约束条件下，力争实现所设定的目标（车辆所走的路径最短或者花费最少）。

将现实问题转化为数学模型，可以将VRPTW表述为m 辆车，从车场0 启程按照设定好的实践访问n 个客户进行运送货物的问题。设di（i=1，2，…，n）为客户i 的需求数量；cij（i，j=1，2，…，n）为车辆从顾客i 到顾客j 的运送花费，如果i=0 或是j=0，那么就表示从配送中心到某部队或是从某部队到配送中心；bk为车辆k 的装载数量；设定的时间窗为［ei，li］；si代表配送车辆抵达客户i 的时间；ti为配送车辆在卸载物资之前的停留时间；tij为配送车辆从客户i 行进到客户j 的消耗时间；μi为卸载物资所消耗的时间；第k 辆车对nk个客户实行了服务，Rk为它的行进线路，rki表示Rk其中的一个客户，在其行进线路里排位为i，rk0和rk（nk+1）都代表配送中心；这里将所有车辆的速度统一为v。

根据相关的设定以及相应问题的描述，可以建立数学模型如下：

其中：式（2）是目标函数；式（3）表示每个配送车辆服务的所有客户的总的需求量不大于车辆的额定运载量；式（4）代表行进的每一个线路上的客户数量不大于总的客户数量；式（5）表示每一个客户都要被访问到；式（6）代表配送车辆行进线路上服务到的客户；式（7）表示每个客户只能被一个配送车辆服务；式（8）代表配送车辆抵达客户i 的时间点加上车辆在客户i 的卸载前的停留时间，加上其卸载的时间，加上从客户i 到客户i+1 的行进时间，即为抵达客户i+1 的时间点；式（9）表示车辆在客户i 的卸载前的停留时间为正数；式（10）表示配送车辆k必须要在最迟限定时间抵达；式（11）表示在第k 辆车服务的客户不小于1 时，该车参与了任务，这个时候sign（nk-1）=1，而在第k 辆车服务的客户小于1时，代表该车没有参与任务，这个时候sign（nk-1）=0。式（12）代表惩罚函数，代表配送车辆要在限定时间抵达，这个已经在前节详细说明了，在此不多赘述。

2 基于量子计算的蚁群算法设计

2.1 量子计算原理及运用

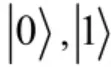
一个量子比特能够同时储存0 与1，那么拥有m 个量子比特的量子位就能够储存2m种可能的数据，拥有m 个量子比特的个体j 的概率幅度能够表达为

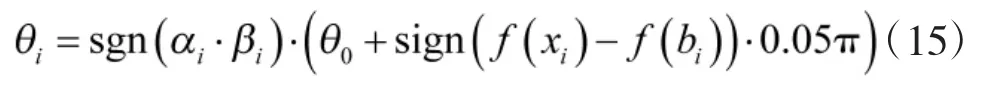
2.2 算法设计

针对在求解VRPTW 时蚁群算法存在的缺陷，本文改善蚁群算法以提高其求解VRPTW 的性能。

2.2.1 转移概率的改进

蚂蚁k 依据转移概率pijk随机选择的节点，这里将pijk设定为：

其中，dij代表节点i 与j 节点之间的距离；β（β≥0）是吸引度因子，代表吸引度的重要程度，β 的值越大，蚂蚁就会更倾向于沿着路程较短的线路前进；μj是客户点上量子信息的强度，它的表达式为

2.2.2 信息素更新方式

针对蚁群算法在信息素更新过程中存在的问题，这里依然使用局部信息素更新和全局信息素更新相结合的信息素更新方式，并且，全局信息素更新添加了量子计算的新模式。

1）局部更新

在构筑最优路径的过程中，蚂蚁每经过边（i，j）都会依照下面的信息素更新公式来更新这条边上的信息素：

2）全局动态更新

当迭代一次完成后，按下式对此次迭代得到的最优路径上的信息素实行全局更新：

式中，Q 是一个（1≤Q≤10 000）的常数。

2.2.3 局部搜索策略

为了能够增加算法的开拓性，本文在所有车辆对路径选择完成之后选用2-opt 搜索作为局部搜索的策略，而2-opt 搜索只用于一辆车所选择的路径之中。

2.3 算法运行步骤

Step 4：信息素的局部更新。每当车辆实行一次选择，就依据式（19）对之前行驶的路径（i，j）实行信息素的局部更新。

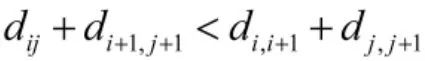
Step 6：对所有蚂蚁的目标函数值Zk（k=1，2，…，m）实行计算，记录当前最优化的解；

Step 7：依据式（20）对各个边的实行信息素的全局更新；

Step 8：运用式（21）更新节点上的量子信息；

Step 10：如果t＜tmax，那么转Step 2；

Step 11：输出当前的最优解。

3 实例仿真

3.1 问题的提出

某公司周年庆典，其下属实体店铺都要承担一定促销活动，公司对下属实体店统一进行货物配送，配送中心根据各个店铺申请的器械与物资，以及各店铺担负任务的重要程度，对其进行有力的配送保障，将店铺所需器械、物资按照限定好的时间送到各个店铺，为了简化便于求解，这里设定配送中心仅有一个，而共有11 个店铺参与任务，设定配送中心编号为0，11 个店铺随机编号1 到11，根据各店铺需求配发至各店铺的器械、物资重量以及设定时间窗如下页表1 所示，重量单位为吨（t），配送中心与各店铺的距离以及各店铺相互之间的距离如表2 所示，单位为公里（km），车辆额定的载重量bk为10 t。根据配送的实际情况，结合各店铺申请的信息，上级部门如何统规协调，才能使各配送车辆的线路与抵达店铺的时间节点合理化，在满足设定好的时间窗的情况下，运用最少的配送车辆，使车辆的总行程最短、成本花费最少，并且能够保证任务的圆满进行。

表1 各店铺需求量

表2 配送中心与店铺以及店铺与店铺之间的距离表

3.2 案例的概括归纳

为了使案例的研究能够对更多现实问题的求解都有一定借鉴作用，可以将案例的问题条件归纳为一种带时间窗的配送车辆路径问题模型：

1）通常供应保障的配送中心为一个，并且配送中心和各个店铺的位置都是已知的，所有配送车辆从配送中心启程，将货物送达各店铺之后，返回配送中心。

2）参与任务的全部店铺都申请了器械和物资，它们的需求量不为0，车辆运载的物资是可以混装的（为配送中心配发的不同类型的器械和装备）；

3）配送中心按照各店铺申请的物资数量以及要求时间统规协调，派遣车辆物资送到各个店铺，根据各店铺的需求，配送中心对各店铺配送物资的数量是已知的；

4）不考虑车辆的运行状态以及发生故障等情况，其种类、型号、速度都设为一致。车辆运载物资的最大载重量是已知的，并且车辆运载物资的数量都是按最大载重量装载物资；

5）每个店铺对于器械物资的申请都有着时间的限定，设定的时间由上级单位依据各店铺的申请结合总体状况进行决定，在设定的时间窗中，如果设定的为硬时间窗，有时候得不到一个可行解，因而，多数情况为了能够得到可行的方案，都是设为软时间窗。

6）器械物资供应充足。首先在应对一些紧急任务时，上级单位以及配送中心都有相应准备，保证有着充足的器械物资可以保障各个店铺，不会出现供应量不足的状况。

7）一个店铺只能由一辆车且只能由一辆车完成配送任务，当车辆运载的物资剩余量满足不了下一个店铺的需求时，车辆返回配送中心。

8）当所有店铺的需求都得到满足，配送任务完成之后，所有的车辆全部返回配送中心。

3.3 对案例的求解

使用Matlab 进行编程，并在CPU 为Inte（lR）Core（TM）i5-4460 CPU@3.20 GHz 3.20 GHz，内存8 G的计算机上运行。实验参数设置为：ρ1=0.1，ρ=0.1，α=1，β=2，γ=1=1，θ=1，tmax=100。运行6 次，得出结果如表3 所示。

表3 多次实验所得结果

多次对实例进行求解，第2 次得出的结果最为优化，路程最短，其车辆的路线及各路线里程如表4所示。

表4 车辆路线及里程表

4 结论

本文首先对VRP 问题的理论进行了研究，引出VRPTW 问题，并且对其进行了数学模型的建立，然后在基本蚁群算法的基础上，改进算法使其能更好地对所建模型进行求解，最后根据实际案例建立模型，运用改进后的算法进行求解，得出本文算法无论是运算结果还是花费的时间，都体现出了更佳优越的性能。