数形结合更入微

薛维惠 丁君华

【摘要】数形结合是一种非常有用的思维方式，借助具体的形把抽象的数学问题化隐为显，变得可视、可指、可表述，依托有形，想象变化，使学生的抽象思维、逻辑思维和空间想象能力因为有一定的物化支撑而得到有效提升，切实提高学生分析问题和解决问题的能力。

【关键词】数形结合  动态变化   空间想象

“数”和“形”是数学中的两个最古老也是最基本的研究对象，它们虽然存在于两个系统中，但又是一一对应的。“数形结合”就是将抽象的数学语言和直观的图形相结合，将形象思维和抽象思维相结合，从而使复杂问题简单化、抽象问题具体化，由表及里去探寻知识本质，寻找优化策略的数学思想。小学阶段的学生思维以形象直观为主，教学中教师要重视把枯燥复杂的数学问题转化成形象直观的图形，让学生感受数形之间的美妙契合，找到解题的方法。数学的学习不是简单的操作模仿，如何在数学教学中应用“数形结合”思想，帮助学生丰富内心体验，实现自主建构，从而优化学生的学习呢？笔者结合教学中的一道练习，粗浅地说说自己的一些思考。

一、聚焦问题——困于遁形的正方形

“明明在一张长8厘米，宽5厘米的长方形纸里剪了一个最大的正方形，这个正方形的边长是多少厘米？”这是三年级《长方形和正方形》单元的一道數学习题，旨在让学生通过练习进一步了解长方形和正方形的特征及联系。从低年级整体直观感知到三年级深入建构长方形和正方形的特征，对学生来说，是一个质的变化，需要强大的空间观念作为支撑。事实上，三年级学生的空间观念有限，遇到这样的实际问题往往束手无策，不知从哪里开始思考。所以，分析练习时往往教师讲得口干舌燥，学生还是一头雾水。等到下次遇到这种类型的习题，又有一大批学生举“白旗”投降，随便填写答案。追问其原因，是因为上次答案填的是这个数，真是令人抓狂。细细分析原因，其实看似简单的问题对学生来说还是抽象的，学生在解答这题时，思维往往停留在机械、呆板的模仿阶段，知道在长方形中剪一个最大的正方形，正方形的边长等于长方形的宽，但为什么边长会等于宽？为什么不能更大些？这个长方形能不能剪出其他的正方形？这些问题没有得到真正解决，说明学生对长方形和正方形之间的关系还没有真正认识透彻。再深入分析一下，面对一个长方形，为什么学生不能自己找到那个最大的正方形？是因为正方形的无形，学生看不见摸不着，感觉不到它的存在，所以抽象、难懂，这对学生的空间观念确实是一个挑战，因此只靠教师讲解，缺少学生自己的数学思考和理解，这样的数学学习苍白无力，因此让学生产生了“山穷水尽疑无路”之感。

二、探寻策略——想象动态的正方形

如何带领学生走出“困境”，让简约变得不简单，让数学学习经验丰富起来呢？实践证明，数形结合就是一种非常有用的思维方式，由数及形，因形寻法，借助具体的形把抽象的数学问题化隐为显，变得可视、可指、可表述，从而使学生的抽象思维、逻辑思维和空间想象能力因为有一定的物化支撑而得到有效提升，提高了学生分析问题和解决问题的能力。“问题就在那里，你必须解决它。”（希尔伯特）学生完成练习的过程，便是探索的过程，教师要引导学生努力寻求策略——不妨画个示意图，在数与形的灵活变换中找到联系，尝试解决问题。

具体教学如下：

师：同学们，这是一个长8厘米，宽5厘米的长方形纸（图1）。如果让你用剪刀能不能剪出一个正方形，你能剪出边长是多少厘米的正方形？

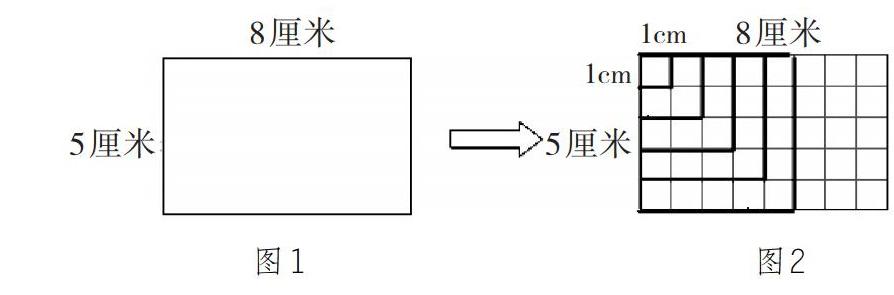
生：能剪出边长5厘米的正方形。

师：只能剪出边长5厘米的正方形吗？你还能在这个长方形里看到其他的正方形吗？现在教师把这个长方形沿着长、宽分成边长是1厘米的方格，长是8格，宽是5格（图2），你在长方形中看到正方形了吗？

生：我看到了边长1厘米的正方形。

生：我看到了边长2厘米的正方形。

生：我看到了边长3厘米、4厘米、5厘米的正方形。

（教师在图中沿着方格线画出来）

师：哦，原来在这个长方形中藏着好多正方形呢，有边长1厘米的正方形，边长2厘米的正方形，边长3厘米、边长4厘米、边长5厘米的正方形。其中最大的是边长几厘米的正方形？

生：边长5厘米的正方形。

师追问：能不能剪出边长6厘米的正方形？为什么？

生：（观察直观图）不能，边长6厘米的正方形，长够剪，但宽没有了。

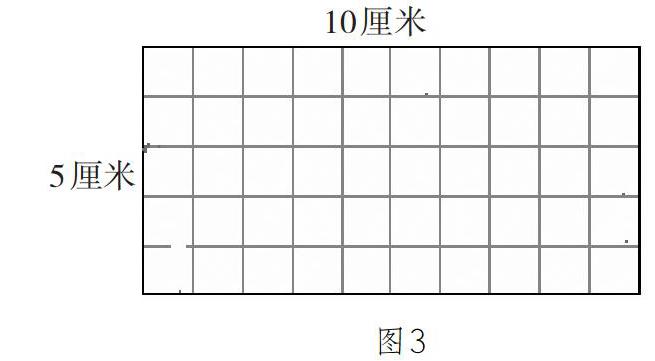
师：现在教师再把长延长至10厘米（图3），想一想，你能看到边长几厘米的正方形，最大的正方形边长是多少厘米？

生：我看到了边长1厘米、2厘米、3厘米、4厘米、5厘米的正方形，边长是5厘米的正方形最大。

师：为什么长变长了，最大的正方形边长还是5厘米？

生：因为宽只有5厘米。

师：如果宽不变，长变成20厘米，剪出的最大正方形边长是多少厘米？

生：边长5厘米的正方形。

师：如果长不变，宽变成7厘米，剪出的最大正方形边长是多少厘米？

生：剪出的最大正方形的边长是7厘米。

师：还能剪出边长是多少厘米的正方形？

生：还有边长是1厘米、2厘米、3厘米、4厘米、5厘米、6厘米的正方形。

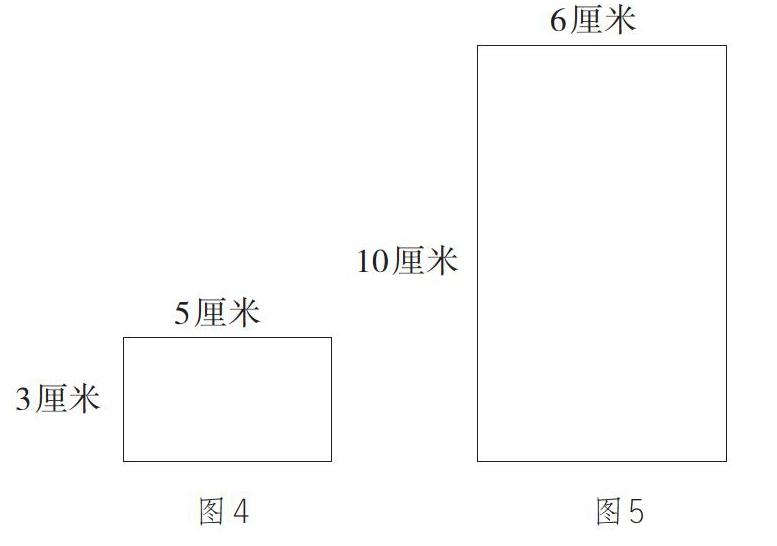
师：在下面的长方形中，能画出哪些边长是整厘米数的正方形？最大的一个正方形边长是多少厘米？

生：在图4中能画出边长1厘米、2厘米、3厘米的正方形，最大的正方形边长3厘米。

生：在图5中能画出边长1厘米、2厘米、3厘米、4厘米、5厘米、6厘米的正方形，最大的正方形边长6厘米。

师：想一想，长方形中剪一个最大的正方形，正方形的边长和什么有关？

生：在长方形中剪一个最大的正方形，正方形的边长等于长方形中较短边的长度。

师：随着我们以后进一步学习，就会知道在长方形中除了能找到边长整厘米数的正方形，还能找到无数个边长不是整厘米数的正方形。

三、反思与解读——数形结合，柳暗花明

1.依托有形，有序建构

如何让藏于长方形中的抽象正方形现身？本案例中，教师别出心裁地将长方形置于方格纸中，借助直观的方格图，一个个有形的正方形跃然纸上，学生面对可以感受到的正方形，自然能一下子找到那个最大的正方形了。当然，让藏匿的正方形现形，这只是第一步。依托这张方格纸，教师不断让学生的思维走向深入：长变化，宽不变，剪出的最大正方形为什么没有变化？如果长宽都变化了，此时能剪出的最大正方形又是怎么變化的？让学生借助图形直观感受数与形的变化，在变与不变中感悟长方形和正方形之间的紧密联系。进而，离开方格纸，寻找那个空白长方形中最大的正方形，此时这个无形的正方形已在学生脑中悄然着陆，变得有形可感，长方形和正方形之间的联系也走向了深入，空间观念的建构也变得扎实、有序。

2.依托动态，灵动生长

“在长10厘米、宽6厘米的长方形中，边长2厘米的正方形还可以怎么剪？一定只能剪6个不同的正方形吗？”这样的变化是否要让学生感觉到？又该如何渗透？笔者认为，可以借助多媒体手段，让学生直观地看到边长2厘米的正方形在长方形中有序地运动，还可以动态地演示正方形边长由1厘米逐渐变化为6厘米的过程，让学生初步感受到其实不仅仅只有6个不同的正方形，内含着无数个正方形，最大的正方形边长是6厘米。这样动态地呈现，学生的思维视角也渐趋开阔：所能看到的正方形可以移动位置、大小可以不断发生变化。数学空间观念的培养离不开想象，这样以直观的变化来促成学生想象视角的变化，以运动变化的视角来展开想象，展开思维，对学生的震撼是强烈的，感受是深刻的，无疑打开了想象的新天地，空间观念得以灵动地生长。当然，这样的动态呈现切忌矫枉过正，需要把握教学的度，适当给学生些开放的视角，点到即可。

“数缺形时少直觉，形少数时难入微。”当直观的图形和抽象的问题相结合，学生也就找到了解决问题的脚手架，数学在他们的眼中也会随之变得简单而丰富。图形、动态虽只是依托，但恰恰是这些不可少的巧妙依托，能架起学生思维与学科知识过渡的桥梁，让学生实现稳稳地着陆——进行深刻地思考，扎实地建构，灵动地生长。