联合平滑矩阵多变量椭圆分布的稀疏表示算法
2019-09-15邱虹王万良郑建炜
邱虹 王万良 郑建炜
信号稀疏表示是过去近20 年来信号处理方向一个非常引人关注的研究领域,目的是在给定的超完备字典中用尽可能少的原子来表示信号,从而获得信号更为简洁的表示方式,方便进一步对信号进行压缩、编码等加工处理.随着压缩感知理论[1]提出在所求系数足够稀疏时,最小化l0范数的NP 难题[2]可以转化为最小化l1范数来进行求解,稀疏表示已广泛应用于机器学习、计算机视觉、模式识别等领域.
在模式识别领域中,具有代表性的是Wright等[3]提出的一种基于稀疏表示的分类器(Sparse representation-based classifier,SRC),该分类器将稀疏表示成功应用于人脸识别,有效解决了人脸图像中遮挡、光照等问题.其核心思想是通过选取完整的输入样本作为训练样本构造出超完备字典,并由此得到测试样本的稀疏表示,然后逐类构造出测试样本的近似线性表示,最后寻找最小重构误差的类别标签作为测试样本的类别归属得以完成分类任务.Wright 指出SRC 对数据缺损不敏感,当重构编码系数足够稀疏时,特征空间的选取变得不再重要,这些特点使得SRC 成为一种优秀的分类算法,且在图像分类研究中获得了成功应用.但是,该算法仍然存在两个关键问题有待关注:1)选择l1范数作为编码重构系数的稀疏约束是否是比较合适的策略;2)选择Frobenius 范数(F 范数)作为线性重构表示的约束是否对图像表示足够有效.基于此,众多科研工作者致力于这两个问题的研究.
Yang 等[4]重新探究了l1范数在模式识别任务中的作用,发现l1范数比l0范数能提供更多有意义的分类信息,即l0范数只能实现稀疏,而l1范数不仅能实现稀疏,还能保持数据间的协作关系.对此,Zhang 等[5]通过理论分析和实验验证解释了SRC分类器获得优秀分类性能的根本原因并非它的稀疏性,而是数据间的协作关系,并提出了协作表示分类器(Collaborative representation-based classifier,CRC).其中,CRC 用l2范数替代SRC 中的l1范数,在不降低识别率的前提下大幅度提升了算法的运行效率.此外,为了加快稀疏编码过程,相继提出了许多基于加权l1或l2范数的算法[6−8].
上述算法均采用F 范数作为线性重构表示的约束.诸多学者认为,找到合适的方式来描述重构误差的特性有利于重构及分类性能的提升.Lu 等[9]考虑到F 范数对大规模异常点的处理较弱,采用l1范数对误差重构进行评估,实验表明l1范数比F 范数对误差的评估更可靠.Naseem 等[10]则利用Huber 估计处理一些随机的光照和噪声像素将所提线性回归分类器(Linear regression classification,LRC)扩展为强健的线性回归分类器(Robust LRC,RLRC)[11],提升了LRC 在多光照及噪声下的鲁棒性.Yang 等[12]采用M 估计匹配一般的噪声,提出了强健的稀疏编码算法(Robust sparse coding,RSC).随后,Yang 等[13]从样本特征的概率分布形式出发,对不同的特征添加贡献度因子,提出正则化鲁棒编码算法(Regularized robust coding,RRC),其具有更高的抗噪能力,却丢失了样本的局部分布特性.而He 等[14]利用相关熵对处理噪声和噪点的稳定性优势,提出一种基于相关熵的稀疏表示算法(Correntropy-based sparse representation,CESR).随后,He 等[15]又构建了半二次框架,该框架结合两种现有的稀疏健壮回归模型:以SRC 为代表的应对误差修复的相加模型和以CESR 和RSC为代表的应对误差检测的相乘模型.通过分而治之的策略,He 等[16]将健壮人脸识别的过程分解为异常值检测和人脸识别两个阶段,使得稀疏表示适用于大规模数据库.
实际上,以上算法均属于多元分析的范畴.众所周知,多元分析是研究多个自变量与因变量相互关系的一组统计理论和方法.其应用的限制条件是,各个因素每一水平的样本必须是独立的随机样本,其重复观测的数据服从正态分布,且各总体方差相等.总体来说,上述这些算法均假设误差向量满足正态性或独立性,但这并不适用于现实场景,特别是在部分随机误差向量的分布呈现出重尾现象的情况下.对于这种情况,Kibria 等[17]提出基于多元t 误差的线性模型.Basu 等[18]使用多元幂指数分布作为语音识别领域的重尾分布.Liu[19]则假定观测的数据是相互依赖的,且将多元幂指数回归模型扩展为矩阵变量幂指数回归模型.这些研究意味着假定观测数据之间相互依赖且服从重尾分布对于描述一些实际观测具有现实意义.事实上,人脸图像中例如光照、遮挡或表情等噪声数据之间高度相关,并不完全服从于独立同分布.因此,找到一种合适的针对矩阵变量的分布来描述误差矩阵的特征至关重要.
本文旨在解决部分遮挡和受光照影响的图像的重构及分类问题.传统方法往往将图像以向量的形式进行存储分类,忽视了图像数据的内部结构信息,且它们依据最大似然估计的观点假设噪声数据服从独立同分布对误差进行处理,不适用于现实场景.本文所提模型强调误差矩阵中各个像素间的依赖性并假定该误差矩阵作为一个随机矩阵变量服从于矩阵多变量椭圆分布.同时,假定模型中的编码重构系数服从拉普拉斯分布或高斯分布.由于通过假定所得的模型具有非光滑性,不利于问题的优化求解,本文引入辅助变量光滑模型,随后采用迭代加权最小二乘法优化求解模型.至此,本文得到一种新的稀疏表示算法,称为联合平滑矩阵多变量椭圆分布的稀疏表示算法(Sparse representation with smoothed matrix multivariate elliptical distribution,SMED).
本文后续结构安排如下.第1 节介绍多变量分析的相关工作,包括多元分布和矩阵多变量椭圆分布.第2 节具体描述SMED 算法的目标函数,并给出模型优化求解的方案.第3 节对SMED 算法的收敛性以及复杂度进行分析.第4 节选择代表性的人脸数据库验证SMED 的实际重构和分类性能.最后,第5 节总结全文工作并给出后续展望.
1 相关工作
本节比较几种常用的多元分布并对矩阵多变量椭圆分布进行简要介绍.
1.1 多元分布比较
不同于以往的算法,本文旨在找到一种合适的能够描述人脸图像中例如光照、遮挡或表情等噪声数据特征的分布.由于现实图像中的噪声数据均表现出尖峰重尾的特征,这就需要找到一种更具适应性的分布来满足这一需求,以减少异常值的影响,提高鲁棒性.图1 给出了几种常用多元分布的比较图.由图1(d)可知,二维拉普拉斯分布及二维幂指数分布较二维高斯分布更具尖峰重尾性,且图1(c)中二维幂指数分布的重尾范围大于图1(b)中的二维拉普拉斯分布.此外,通过三者在XOY面上的投影图可知,二维高斯分布的投影面呈圆形形状,二维拉普拉斯分布的投影面呈菱形形状,二维幂指数分布的投影面呈椭圆形形状,而椭圆形形状能够很好地兼具圆形和菱形的特点,这使得二维幂指数分布更具灵活性,且椭圆形形状较圆形和菱形使得分布具有更肥的尾部区域,故而对于异常值更具鲁棒性.综上所述,相对于二维高斯分布和二维拉普拉斯分布,二维幂指数分布能更好地描述噪声数据的特征.
事实上,二维幂指数分布作为Kotz-type 分布[20]的特例是椭圆分布家族中的一员.近年来,椭圆分布被诸多学者证明是一种作为多元高斯分布、多元拉普拉斯分布的有效替代,它在统计学、金融学、信号处理以及模式识别等领域中发挥着重要作用,尤其在鲁棒性研究以及数据包含异常值或呈现出重尾现象的情况下表现更加突出[21].依据文献[22−24]可知,在一些随机现象真实场景中,部分随机向量的分布数据往往包含异常值或呈现出长尾、重尾现象,而椭圆分布对于这些现象具有较好的适应性.例如:Liu 等[25]针对一般的非正态数据,提出基于幂指数分布的多元回归模型,扩展了对于随机误差的一般分布假设.Sun 等[26]利用重尾椭圆分布对数据的结构协方差矩阵提供鲁棒估计.此外,Fang等[27]提出除了多元正态分布,椭圆分布家族中的其他多元分布均能很好地描述随机矩阵中各个元素间的依赖关系.因此,假设误差矩阵服从椭圆分布来描述图像中的噪声数据能够更接近数据的固有特性,即噪声像素间的依赖关系.
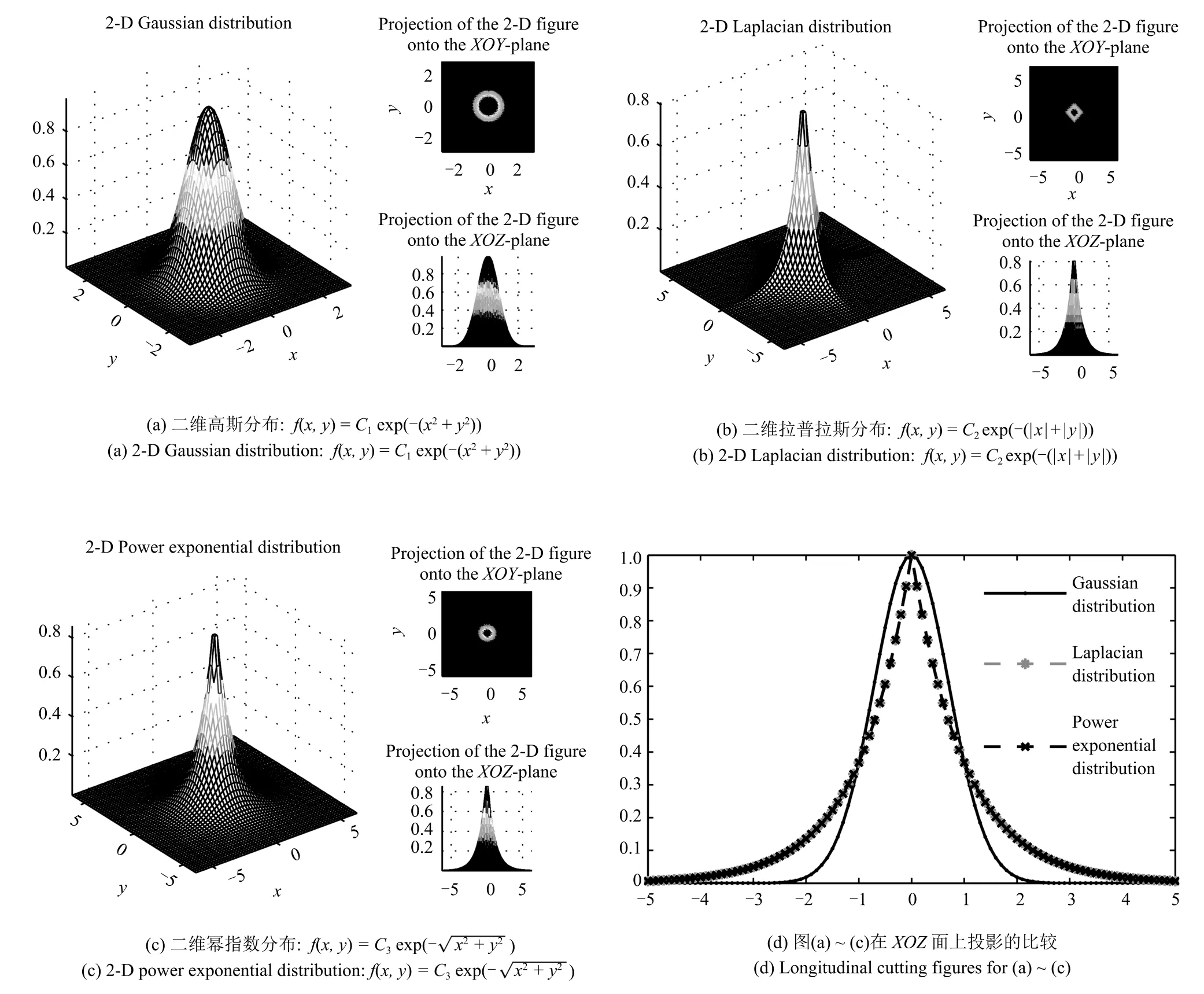
图1 多元分布比较图(常数取Ci=1, i=1,2,3)Fig.1 The comparison chart of the multivariate distribution(where the constants are Ci=1, i=1,2,3)
1.2 矩阵多变量椭圆分布
椭圆分布[28]作为概率分布家族中的一员,允许同时考虑大量非高斯分布,并且对典型未知数据的协方差矩阵提供最佳的估计,能够有效构建误差结构.本小节简要介绍多变量椭圆分布和矩阵多变量椭圆分布的定义.
定义1.给定x ∈Rn是一个n维随机向量,如果对于某个µ ∈Rn和某个对称正定矩阵Σ∈Rn×n,x的特征函数具有如下形式:
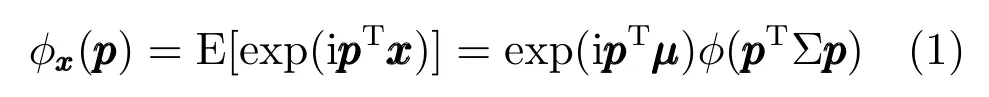
其中,E[·]代表期望值,φ(·)是一个标量函数,称为特征生成元,φ(·):R→R,且p ∈Rn.则称x服从具有分布参数µ、Σ 和φ的n维多变量椭圆分布,记为x ∼En(µ,Σ,φ).
定义2.给定X ∈Rm×n是一个m×n维随机矩阵,如果对于某个矩阵M ∈Rm×n和某个对称正定矩阵Σ∈Rm×n,X的特征函数具有如下形式:
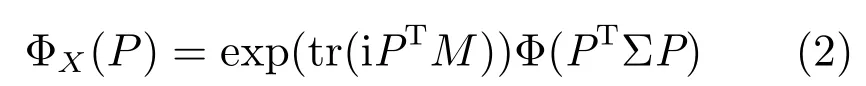
其中,Φ(·)是特征生成元,Φ(·):Rn×n →R.则称X服从具有分布参数M,Σ 和Φ 的m×n维矩阵多变量椭圆分布,记为X ∼Em,n(M,Σ,Φ).
依据定义2 可知,矩阵多变量椭圆分布是一种对称概率分布,也可通过概率密度函数对其进行定义
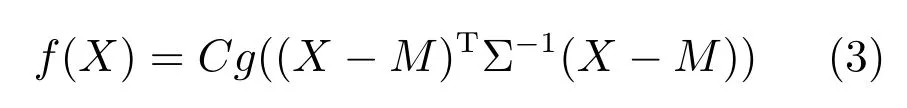
其中,C是正数,特征生成元g(·):Rn×n →R.
随机向量、随机矩阵的特征函数总是存在的,并且与概率密度函数存在一一对应的关系.因而椭圆分布的特征生成元一旦确定,其分布的概率密度函数形式就确定了,例如:当特征生成元φ(·)的形式为φ(x)=exp(−x/2)时,x服从多元正态分布.椭圆分布包括的多元分布有:多元正态分布、多元柯西分布、多元拉普拉斯分布、多元logistic 分布、多元student 分布以及部分多元稳定分布等.本节参考文献[29]中的特征生成元,选择g(·)=exp(tr(−(·)k/2)),k >0,该g(·)不仅保持了拉普拉斯分布对异常值的鲁棒性,而且具有长尾特性.将g(·)=exp(tr(−(·)k/2))代入式(3)中,可得:
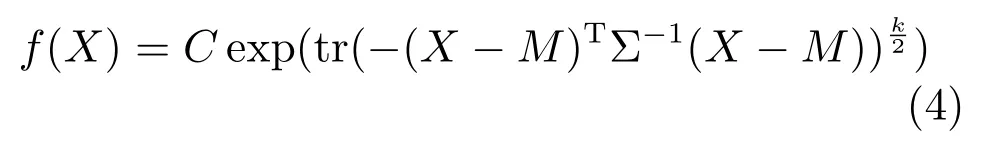
本文将以此概率密度函数为基础构建目标函数,并辅以平滑目标函数、加快迭代最优过程等优势.
2 SMED 算法描述
本节提出一种联合平滑矩阵多变量椭圆分布的稀疏表示算法,简称SMED.首先对该算法目标函数的构建过程进行描述,然后给出模型求解的优化方案.
2.1 目标函数构建
探索人脸图像数据中误差矩阵的内部结构是重构及分类识别任务的一项成功策略,受椭圆分布启发,采用矩阵多变量椭圆分布描述误差矩阵,具有更直观的物理意义和求解思路.
给定n个p×q维图像矩阵将其作为训练样本.其中,代表第c类的第i个样本矩阵,样本总类别数为C,ni是第i类的样本个数,且n=n1+n2+···+nC是总样本数,测试样本表示为图像矩阵Y ∈Rp×q.
将任意测试样本Y通过训练样本进行线性表示,可得
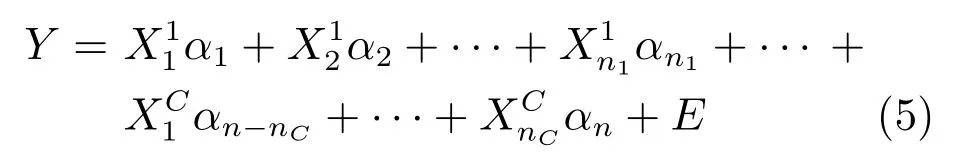
其中,α=[α1,α2,···,αn]∈Rn是训练样本所对应的重构编码系数,为n×1 维列向量,E为误差矩阵.
定义线性映射Rd →Rp×q:
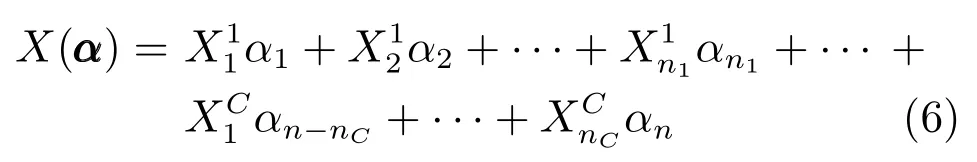
通过式(6),可将式(5)简化为

对应经典的线性向量回归模型[30],式(5)和式(7)给出了线性矩阵回归模型的一般形式.
本文假定误差矩阵E=Y −X(α)∼Em,n(M,Σ,Φ),即服从矩阵多变量椭圆分布,且训练样本所对应的重构编码系数α1,α2,···,αn独立同分布于高斯分布(l=2)或拉普拉斯分布(l=1).则依据最大后验概率估计可得
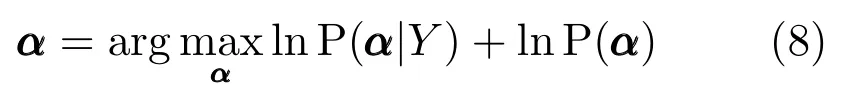
其 中,P(α|Y)=C1exp(tr(−(Y −X(α))T(Y −X(α)))k/2),具体目标函数描述为
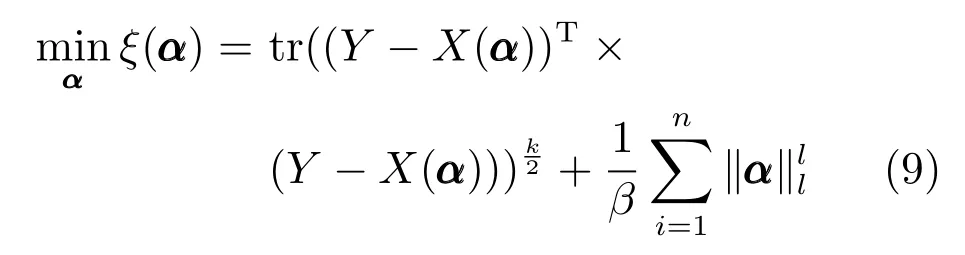
令λ=2/β,且已知矩阵X的核范数表示为向量x的lp范数表示为则可将式(9)调整为
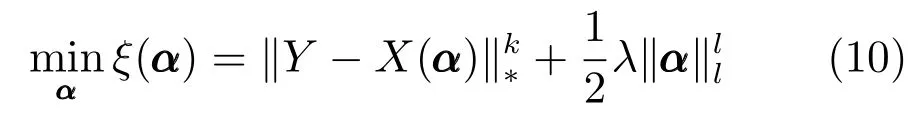
其中,k >0,l=1 或2.当k=1,l=1 或2 时,上式的右边第1 项为核范数,第2 项为l1范数或l2范数的平方,这两项均为非光滑凸函数.此外,当0
然而,由于式(10)具有非光滑性,不利于目标函数的优化求解,本文通过引入辅助变量光滑上式来解决这一问题,则可将一般的平滑矩阵多变量椭圆分布模型归纳为如下优化问题:
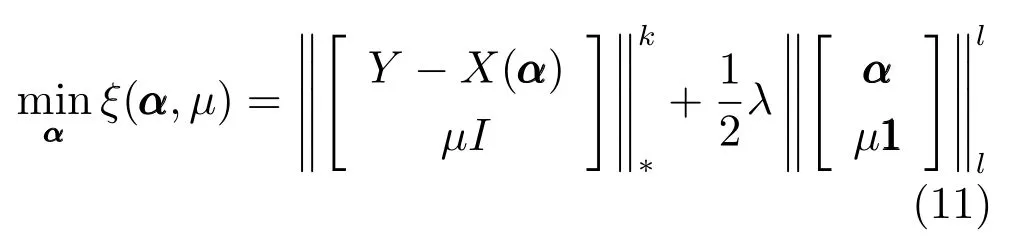
上式能处理的参数范围为µ>0,k >0,k2,l=1 或2,I ∈Rq×q是单位矩阵且111∈Rn是元素值均为1 的n×1 维列向量.
文献[31]和文献[32]中的算法通过不同方法对非光滑目标函数进行了优化求解.相比较而言,式(11)采用µI和µ111 两项辅助变量来光滑目标函数的操作拥有以下优势:1)当µ >0 时,ξ(α,µ)是光滑的,它较非光滑的目标函数更容易进行优化求解;2)当k≥1 时,依据式(11)两项的凸性质可知ξ(α,µ)是一个凸函数,则最小化目标函数即为凸优化问题,可得全局最优解.
此外,根据式(12)可知ξ(α,µ)≥ξ(α),且当且仅当µ=0 时,ξ(α,µ)=ξ(α).这意味着ξ(α,µ)是ξ(α)通过µ的优化函数,如果ξ(α,µ)是递减函数则ξ(α)亦为递减函数.
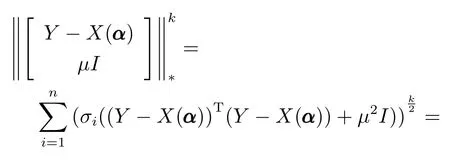
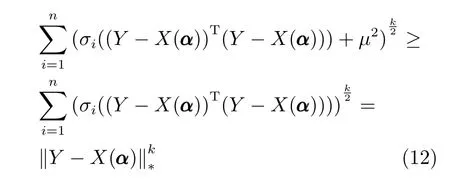
其中,σi(·)代表矩阵的第i个正奇异值.
2.2 模型优化求解
诸多方法可用来优化求解模型(11),例如:半正定规划法(Semi-definite programming,SDP)[33]是在满足约束“对称矩阵的仿射组合半正定”的条件下使线性函数极大(极小)化的问题.加速近端梯度法(Accelerated proximal gradient,APG)[34]是一个求解l1优化问题较快的方法,其收敛速度为二阶收敛,相比较其他方法具有明显的速度优势.交替方向乘子法(Alternating direction method of multipliers,ADMM)[35]又称增广拉格朗日法,是求解约束优化问题的一类重要方法,具有不需要惩罚参数趋向于无穷大等优点[36].然而,SDP 因其算法复杂度高不适用于大规模数据(对于n×n维的矩阵,SDP 的算法复杂度是O(n6)).APG 需要目标函数具有Lipschitz 连续梯度,这使得该方法的使用受到限制.相比较SDP 和APG,ADMM 以其较好的性能和严格的理论保证,成为众多学者研究的热点.但是,ADMM 需要在非光滑目标函数中加入多个辅助变量乘子,这大大降低了算法的收敛速度,且其在优化求解目标函数的过程中需要应用奇异值分解(Singular value decomposition,SVD)[37],增加了算法的复杂度.本节采用迭代加权最小二乘法(Iteratively reweighted least squares,IRLS)[38]对模型进行优化求解,避免了ADMM 需要加入多个辅助变量乘子和进行奇异值分解的缺陷.
依据相关公式,式(11)可优化调整为
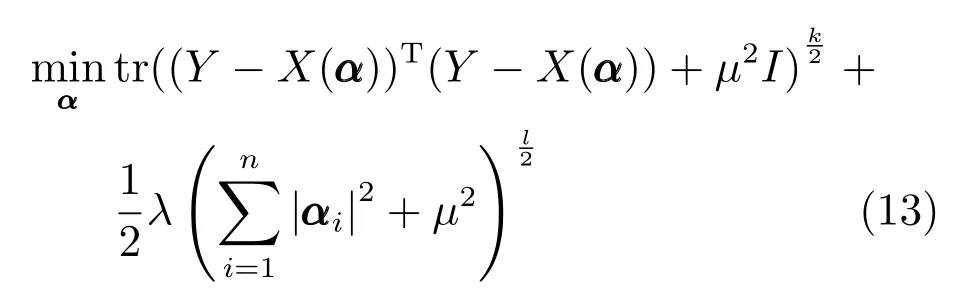
其中,αi代表向量α的第i个元素.
令
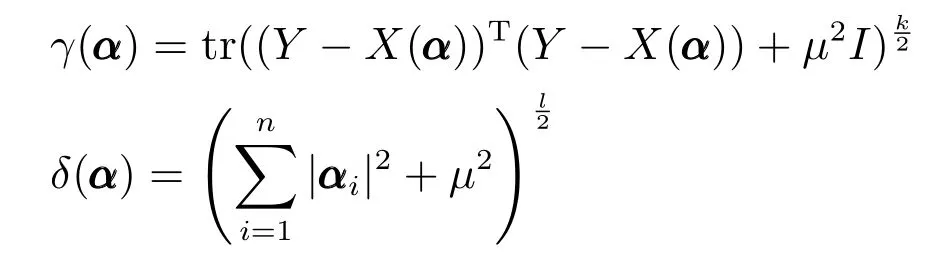
则
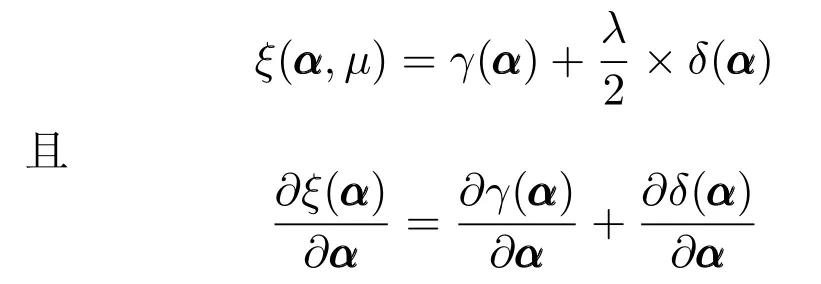
其中,γ(α)针对α的梯度为
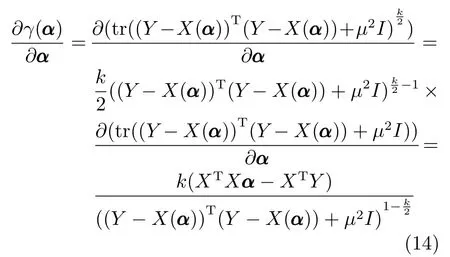
令对应γ(α)的加权矩阵R=((Y −X(α))T(Y −X(α))+µ2I)(k−2)/2,则上式可简化为
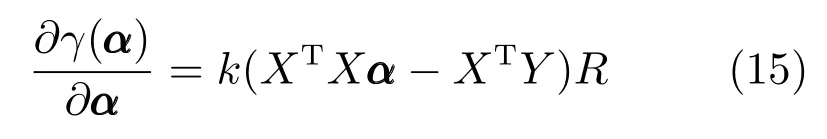
其次,δ(α)针对α的梯度为
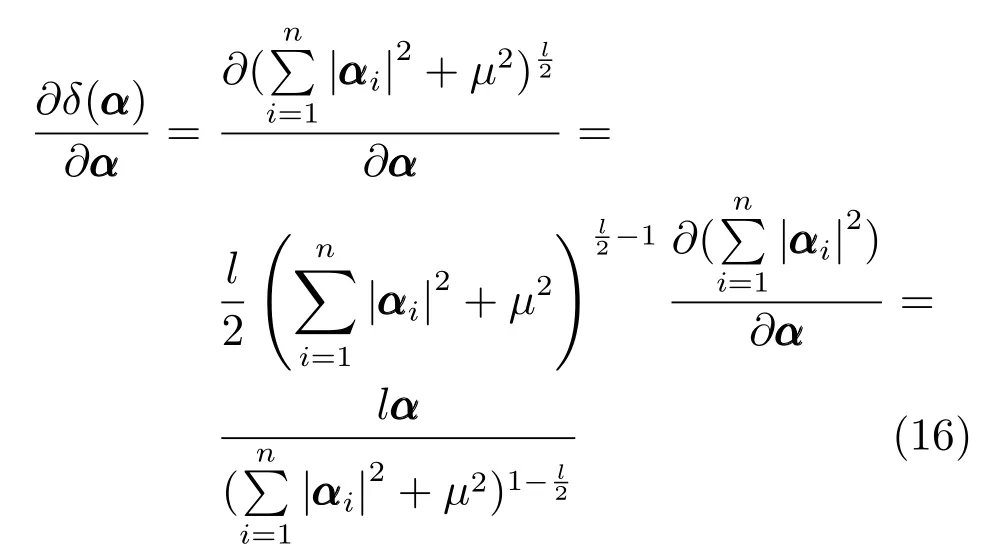
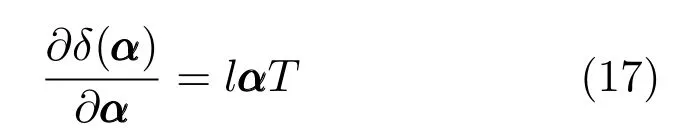
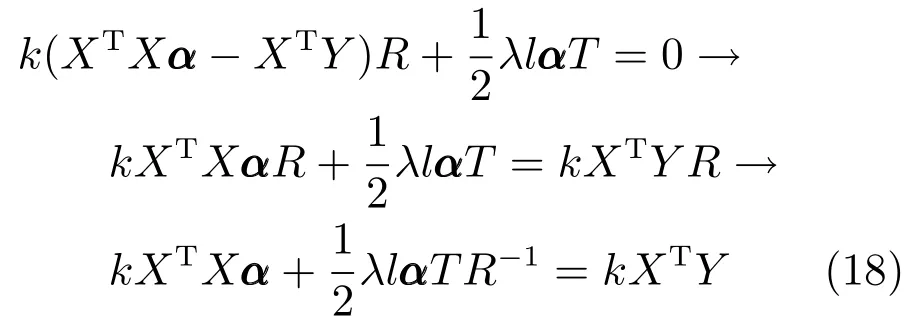
式(18)是经典的Sylvester 方程形式(AX+XB=C),方程求解的算法复杂度是O(n3)[39−40].实验过程中可利用MATLAB 的lyap命令求解式(18).
综上所述,完整的SMED 描述如算法1 所示.其中,Vec(·)代表将矩阵通过列转化为向量的操作,Mat(·)代表将向量转化为矩阵的操作.
算法1.SMED 描述
输入.n个p×q维图像矩阵(n=n1+n2+···+nC);图像矩阵Y ∈Rp×q;模型参数λ >0,µ >0;终止条件参数ε >0.
输出.重构编码系数向量α.
1)令
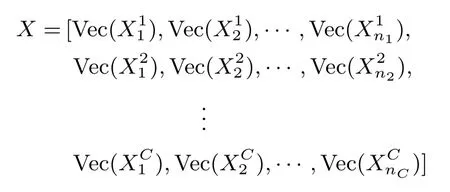
初始化加权矩阵R=I.
2)设迭代次数t=1.
3)固定加权矩阵Rt,Tt,依照式(19)计算更新重构编码系数向量αt+1
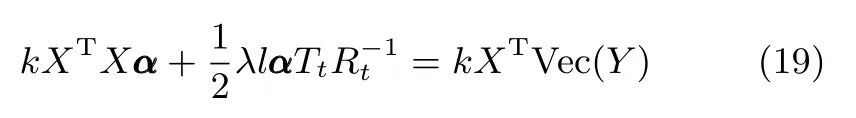
4)固定αt+1,依照式(20)和式(21)分别更新加权矩阵Rt+1,Tt+1
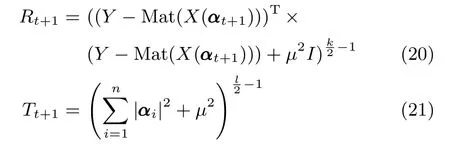
3 收敛性和复杂度分析
SMED 采用迭代加权最小二乘法进行模型迭代求解,在固定部分变量的前提下优化余下未知变量.根据算法1 描述,每次迭代的关键步骤(20)和(21)都是闭式解,因此其单个变量更新都存在唯一解.定理1.说明所提算法在迭代过程中使目标函数(11)的值逐步下降,并最终收敛.
引理1.给定任意矩阵X ∈Rm×n和Y ∈Rm×n,其中,矩阵X和Y的列向量为非零向量.令fi(x),i=1,2,···,n为可微凹函数,可得
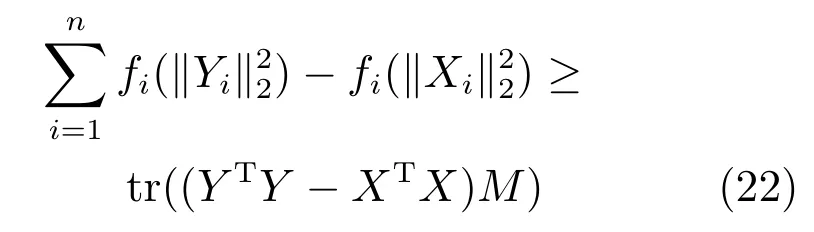
其中,对角矩阵M ∈Rn×n的对角元素为Mii=
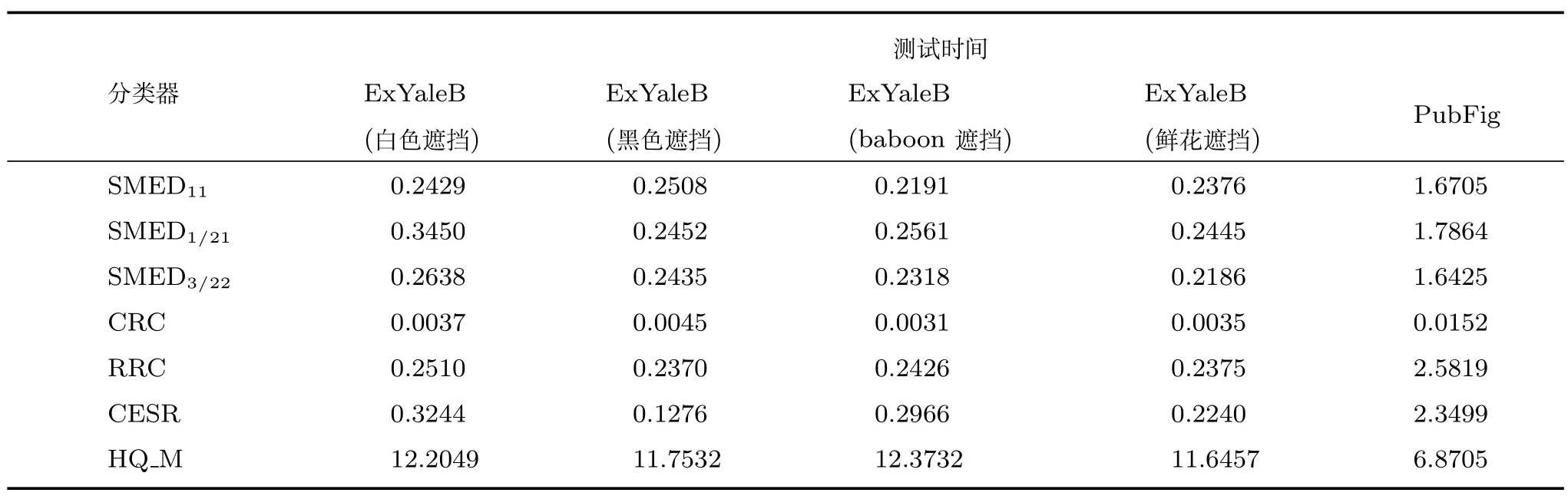
设定fi(x)=xq/2,0 证明.根据凹函数定义文献[41]可知,在定义域(0,∞)中,当p ∈(0,1]时,凹函数xp满足yp −xp+pyp−1(x y)≥0.对矩阵X ∈Rm×n和Y ∈Rm×n,则有 将式(24)中所有的i ∈{1,2,···,n}相加,则式(22)得证. 引理2.给定任意矩阵其中,为对称正定矩阵.令X,Y的特征值λi分别满足λ1(X)≥λ2(X)≥···≥λn(X)≥0 及λ1(Y)≥λ2(Y)≥···≥λn(Y)≥0.则可得 证明.见文献[42]中的引理2. 引理3.给定任意矩阵当p ∈(0,1]时,tr(Xp)为凹函数. 证明.由引理2 可知,对X,有 则通过推论和引理1 可得 由式(26)可知,当p ∈(0,1]时,tr(Xp)为凹函数. 通过上述引理1 可知,假设g(X)为可微凹函数,那么对于X,可得 此外,由引理3 可知,当l ∈(0,2]时,tr(Xl/2)为凹函数.则设定g(X)=tr(Xl/2),将g(X)代入上式可得 定理1.通过算法1 迭代计算,目标函数式(11)的值逐次下降直至收敛. 证明.定义第t次迭代时的误差矩阵Et=Y −X(αt),由于αt+1是式(18)的解,则有 通过对式(29)两边分别点乘αt −αt+1,可得 此外,结合式(23)和式(30)有 将式(31)与式(32)相加可以得到 即目标函数(11)的值在迭代更新的过程中逐次下降,并具有明确的下确界0,则该算法收敛性得证. 定理2.通过算法1 产生的序列αt收敛到最优解α∗. 证明.结合式(25)和式(33)有 上式通过t≥1 次迭代求和得 因序列{αt}有界,故存在和子序列{αtj}使得而作为式(18)迭代过程的其中一解可表示为 式(35)意味着在j →∞的过程中,能收敛到某个 其中,R∗和T∗为对应α∗下的值.至此,收敛到最优解得证. 算法1 的关键耗时步骤是3 个未知变量的更新操作,包括Rt,Tt和αt.其中Rt依式(20)计算,其运算复杂度是O(d),Tt依式(21)计算,其运算复杂度是O(n),重构编码系数αt通过求解式(19)获得,式(19)是一个标准的Sylvester 公式,其求解的典型算法是Bartel-Stewart 法,先通过QR 分解将系数矩阵变换成Schur 形式,再采用回代法求解三角系统,整体运算复杂度是O(n3).一般情况下,dn3,因此,SMED 每次迭代的复杂度是O(n3).假设算法的实际迭代次数是tm,可得SMED 的综合运算复杂度是O(n3tm).通过多次实验发现,迭代次数tm一般满足tm≤30. 为验证所提算法的有效性,以人脸识别为例,分别采用AR[13]、ExYaleB[43]和PubFig[44]三个公开人脸数据库进行实验分析.对SMED 来说,因其模型中k,l的取值范围为k >0,k2,l=1 或2,且当k=1 时,式(10)第1 项为核范数,第2 项为l1范数或l2范数的平方;当0 在本小节中,选用AR 人脸数据库可视化所提算法并对比各算法的重构性能.AR 人脸库包含126人(70 位男性和56 位女性)的4 000 多张彩色图像,图像通过两个不同时段拍摄获取,每个时段每人共拍摄13 张包含在不同表情、光照条件和现实遮挡(墨镜和围巾)下的大小为768 像素×576 像素的彩色图像.与文献[13]类似,本文抽选其中一个子集(50 位男性和50 位女性)作为实验测试.选取每人每时段4 张无遮挡正面人脸图像,即100 人每人8张共800 张图像作为训练样本.此外,构建三个测试样本:1)选取每人每时段3 张在不同光照条件下的人脸图像;2)选取每人每时段3 张在墨镜遮挡下的人脸图像;3)选取每人每时段3 张在围巾遮挡下的人脸图像.3 个测试样本均包含600 张图像(100人每人6 张).本文将AR 人脸库中的图像统一裁剪至83 像素×60 像素.对比算法选用经典的分类器SRC和CRC,抗噪性较强的RRC,能快速提取特征的FFS[45]以及基于半二次相加框架的HQ_A和基于半二次相乘框架的HQ_M[15],实验中SRC,CRC,RRC,FFS,HQ_A 和HQ_M 的参数设置分别参考了文献[3]、[5]、[13]、[15]和[45],且RRC 算法采用识别率较高的l1范数约束. 4.1.1 参数µc 和ρ 的敏感度分析 参数的选择对算法整体运行具有重要的意义.选择适当的参数,有利于加快目标函数的收敛速度并能精确地求解模型.本小节对SMED 算法中参数µ值选择的敏感度进行了分析.实验中通过µt+1=µt/ρ,ρ >1 来递减参数µ,并将µ的初始值设置为因此,参数µ的值取决于µc和ρ.本小节构建两个实验来评估µc和ρ的值对SMED 算法性能的敏感度,其中选择具有代表性的SMED11作为实验对象,测试样本选取第二类包含墨镜遮挡的人脸图像,且统一设置参数λ的值为0.1.图2 所示即为不同参数值及不同迭代次数下SMED11算法的目标函数值.图2(a)固定ρ=1.1,从而评估不同µc值对算法目标函数值的影响,图2(b)固定µc=0.01,从而评估不同ρ值对算法目标函数值的影响. 由图2(a)可知,当µc=0.001 和µc=0.0001时,µc的值极小,对应的算法收敛值曲线显示经过不到5 次的迭代SMED11就达到了收敛,这说明µc的值越小越将导致算法的不精确求解.但是随着µc值的增大,SMED11就需要更多次的迭代才能收敛算法,如图所示,当µc=0.01 时,算法仅需约15 次的迭代就能达到收敛;当µc=0.1 时,需要约40 次;而当µc=1 时,却需要将近约60 次的迭代才能达到收敛.由图2(b)可知,参数ρ值的选择对算法敏感度的情况与参数µc类似.ρ的值越大越将导致算法的快速收敛,使得模型求解不精确,而ρ的值越小越能提升模型求解的精确度.因此,为了兼顾算法对模型求解的效率和精确度,综合图2 的显示情况可知所选参数µc的值不应太小,而ρ的值不应太大.综上所述,本节选取µc=0.01,ρ=1.1 作为实验中的参数值输入. 图2 不同参数µc 和ρ 值下的SMED11算法收敛值曲线Fig.2 Convergence curves of SMED11algorithm on AR with different regularization parameters µc and ρ 4.1.2 可视化重构性能 本小节评估所提算法的重构性能,通过可视化所构建的AR 人脸库的3 个测试样本中的图像来比较SMED11,SMED1/21,SMED3/22和对比算法的人脸重构能力.部分实验结果如图3 所示.图3(a)为重构前的原始图像,从上至下依次为光照影响的人脸图像、墨镜遮挡的人脸图像、围巾遮挡的人脸图像.图3(b)为通过SMED11重构后的图像与对应每类图像的重构误差值其中α∗代表重构编码系数的最优解,则Xα∗为Y的重构图像.δi(α∗)代表α∗向量中除关联第i类的元素含值外其他元素均为零,则Xδi(α∗)为关联第i类的Y的重构图像.而分类识别的原理是ei(Y)=mini ei(Y),即第i类的重构误差值最小,则图像Y就归属于第i类.从图3(b)中可见,圆点为重构误差的最小值,横坐标代表图像的类别,从上至下依次可得在光照影响、墨镜遮挡、围巾遮挡下的人脸图像通过SMED11重构后均归属于第10 人的图像类别,符合实际情况.此外,图3(b)的这三张结果图还说明了光照影响对SMED11算法的分类性能干扰最小,遮挡类的干扰明显大于光照,特别地,围巾遮挡的干扰最大.图3(c)∼3(k)为所提算法与对比算法基于图3(a)的重构图像(左侧)和冗余图像(右侧), 图3 不同光照影响及墨镜和围巾遮挡下的人脸重构性能对比Fig.3 The reconfiguration performance contrast of different algorithms under illuminition changes and sunglass or scraf occlusion 由图3(c)∼3(k)可知,SMED 算法在重构性能上较其他对比算法突出,这揭示了重构编码系数的稀疏性对人脸图像的重构具有一定程度的有效性.而对于SMED11,SMED1/21和SMED3/22这三者而言,从图3(c)、图3(d)和图3(e)的比较中可以看出它们的重构效果非常接近,仅存有细微差别,如对于光照影响,SMED11和SMED3/22的处理效果优于SMED1/21,具体表现在眼睛这块区域的重构;对于墨镜遮挡,SMED1/21重构的图像棱角更为明确;而对于围巾遮挡,虽然三者在眼睛区域的重构都表现不佳,但是对围巾遮挡处嘴巴的修复却表现不错,基本还原了遮挡处的嘴型,而且SMED1/21比SMED11和SMED3/22修复将更清晰.总体来说,对于AR 数据库而言,属于特例的SMED11对光照影响的处理较优,而SMED1/21对大面积遮挡情况的处理表现突出.此外,对于对比算法,从图3(f)和图3(g)可得SRC 和CRC 不太适合遮挡类图像的修复工作,重构的人脸图像都带有明显的光照影响以及墨镜和围巾遮挡.而图3(j)基于半二次相加框架的虽然它的重构效果优于SRC 和CRC,但是同样存在墨镜和围巾的痕迹,且光照影响去除不佳.图3(h)和图3(i)中的RRC 和FFS,前者引入了特征加权特性,后者通过快速提取特征重构图像,其重构人脸有一定程度的光照去除效果,且对于墨镜遮挡,其消除了墨镜效果,但存留明显的眼镜框架,围巾遮挡上RRC 在眼睛区域的重构效果优于FFS,但对嘴巴的修复FFS 比RRC 表现更佳.对于对比算法中表现最佳的基于半二次相乘框架的来说,如图3(k),虽然重构图像的清晰度高于SMED 算法且对光照影响的处理上优于SMED,但是对于遮挡图像,SMED 的修复较更加接近于正面无遮挡无光照影响的原图像,特别是眼睛区域和嘴巴区域. 通过AR 数据库进行真实影响下的人脸识别实验,训练样本和测试样本的选择与第4.1 节一致.实验步骤为:首先采用训练样本和测试样本迭代求解模型中的最优重构编码系数α∗;然后通过α∗和测试样本数据得到重构数据;最后利用分类原理获得每类测试样本的整体识别率.本小节仍然选择第4.1节中的对比算法进行实验且参数设置保持一致. 4.2.1 光照及伪装影响 表1 给出了所提算法和对比算法在真实影响下的识别率对比,其中粗体数据值即为同等条件下的最优识别率.通过表1 可以发现:除在围巾遮挡的测试实验中RRC 算法共享了SMED1/21的最优识别率外,其他情况下SMED 都具有最优的测试值.而对于SMED 来说,SMED1/21在墨镜、围巾遮挡情形下的效果均优于SMED11和SMED3/22,在光照影响下,SMED11表现更突出.这一现象与第4.1.1节表现一致.值得注意的是,在墨镜遮挡情形下效果较优却在围巾遮挡情形下效果较弱,而CRC 则正处于相反的情况.总体而言,在光照影响的样本测试实验中,最优的SMED11较SRC,CRC,RRC,FFS,和分别提升了5.33%,0.50%,7.66%,12.83%,8.00%,2.32% 的识别率.在墨镜遮挡的样本测试实验中,最优的SMED1/21较SRC,CRC,RRC,FFS,和分别提升了8.34%,7.50%,6.01%,11.67%,7.17%,1.34% 的识别率.在围巾遮挡的样本测试实验中,最优的SMED1/21较SRC,CRC,FFS,和分别提升了14.00%,6.33%,19.00%,25.33%,20.90% 的识别率. 表1 AR 人脸库真实影响下不同算法的识别率对比(%)Table 1 Comparison of recognition rates on AR database(%) 4.2.2 像素污损影响 本小节对AR 数据库进行更具挑战性的实验对比.通过对墨镜遮挡及围巾遮挡样本图像进行不同程度的随机像素污损来比较所提算法和对比算法的识别性能.图4 为实验结果图,其中各子图上方显示的即为0%∼50% 像素污损程度下的测试样本图像.由图4 可知,对比SRC,CRC,FFS 和SMED 表现突出,而其与RRC 和的识别率比较呈现竞争状态.总体来说,各算法对墨镜遮挡像素污损图像的识别率均高于围巾遮挡的像素污损图像,符合第4.2.1 节的一般规律,且SMED1/21在不同像素污损程度下较SMED11和SMED3/22突出.此外,从图4(a)和图4(b)可得,随着污损程度的增加,CRC 比SRC 呈现更快的下降趋势,这源于CRC 对于数据间的协作关系描述不适用于处理这类稀疏型噪声.因此,对于像素污损这类稀疏型噪声,SRC 较CRC 更具鲁棒性. 图4 不同像素污损程度下的人脸识别率对比Fig.4 Comparison of recognition rates under the different pixel corruption levels 在本节中,采用ExYaleB 数据库测试SMED在随机遮挡下的人脸识别应用中的算法性能.ExYaleB 包含38 人每人9 种姿态形式、64 种光照变化,总共21 888 张人脸图像.与文献[13]一致,本文抽选其中接近正面,与光照变化有关的2 414 幅图像用于实验.每张图像大小都统一调整至32 像素×32 像素.任意选取其中每个人物20 幅图像共760张作为训练样本,其余为测试样本.对比算法选择在第4.2.1 节表现不错的CRC,RRC 和此外,添加抗噪性较强的CESR[14]算法.CRC,RRC 和的实验参数与第4.1 节一致,CESR 的参数设置参考文献[14].此外,本小节通过参数敏感度分析设置SMED 算法中的参数µc=0.1,ρ=1.1. 实验中,将测试样本做四种不同类型图像的随机遮挡处理:1)不同尺寸大小方形白色图像随机遮挡;2)不同尺寸大小方形黑色图像随机遮挡;3)不同尺寸大小方形baboon 图像随机遮挡;4)不同尺寸大小非方形鲜花图像随机遮挡.遮挡图像的尺寸决定了测试样本图像被遮挡的程度.本小节首先对四种经过遮挡处理的测试样本进行分类识别测验,然后通过图4 比较不同遮挡程度下所提算法与对比算法的识别率,其中各子图上方显示的即为0%∼60% 遮挡程度下的测试样本图像. 由图5 可知,方形白色图像遮挡对各算法识别率的影响较大,而非方形鲜花图像影响较小.此外,方形黑色及baboon 图像对各算法识别率影响的程度相似.具体来说,图5(a)中SMED11表现最佳,虽然在20% 遮挡程度时RRC 的识别率高于SMED11,但当遮挡程度大于30% 时,其识别性能均优于RRC,特别在60% 遮挡程度时,SMED11较RRC 的识别率提升了4.3%.SMED1/21和SMED3/22虽然没有SMED11表现突出,但当遮挡大于50% 时,它们与RRC 的识别率结果不分伯仲.此外,当遮挡低于20% 时,表现不错,识别率高于SMED1/21和SMED3/22,但随着遮挡程度的增加其优势不复存在;同样地,遮挡低于30% 时,CESR 的识别率随遮挡程度的增加递减平稳,基本保持在85%∼90%,此后其识别率急剧下降,特别当遮挡为60% 时,识别率低至6.89%;而对于CRC,随着遮挡程度的增加识别率就开始快速递减,60% 遮挡时,识别率为21.58%,高于CESR.综合图5(a)可得对方形白色图像遮挡表现最佳的SMED11算法在60% 遮挡程度下比CRC,RRC,CESR 和分别提升了22.56%,4.3%,37.25%,16.81% 的识别率.对于方形黑色图像遮挡,图5(b)显示了各算法的识别率对比,可以看出各算法对方形黑色遮挡的处理性能优于方形白色遮挡.特别地,表现突出,非常接近SMED11的识别结果,其在10%∼30% 遮挡时,识别率略优于SMED11,40%∼50% 时,两者识别率基本一致,到60% 时,SMED11显现出高于的识别性能.对于SMED1/21和SMED3/22,虽然它们在低遮挡程度下表现并不突出,但随着遮挡程度的增加,逐渐体现出抗遮挡的能力,尤其在60% 遮挡时,识别结果高于表现不错的SMED11.此外,RRC 并不像在图5(a)中表现的那么出色,反而与CRC,CESR的识别效果类似,表现平平.总体而言,对于方形黑色图像遮挡,在60% 遮挡程度下,识别率最高的SMED1/21比CRC,RRC,CESR 和分别提升了19.52%,12.92%,14.56%,10.22% 的识别率.此外,对于方形baboon 图像及非方形鲜花图像遮挡,图5(c)和图5(d)显示SMED11,SMED1/21和SMED3/22均表现突出.60% 遮挡下,在图5(c)中识别性能最优的SMED1/21比CRC,RRC,CESR和分别提升了33.12%,17.95%,28.02%,11.94% 的识别率.图5(d)中表现最佳的SMED11比CRC,RRC,CESR 和分别提升了8.76%,0.15%,10.44%,0.79% 的识别率. 图5 不同遮挡程度下的人脸识别率对比Fig.5 Comparison of recognition rates under the different occlusion levels 与第4.3 节实验环境一致,本节采用PubFig数据库测试SMED 在非限制场景下人脸识别应用中的算法性能,对比算法仍然选取CRC,RRC 和PubFig 是一个大规模、非限制场景下的真实人脸数据库,包含从网络搜集来的200 人共58 797 幅彩色图像.图像可能受强光光照、自由姿态、障碍物遮挡、配饰遮挡、夸张表情等多种复杂因素的干扰.本文抽选100 人,每人20 张,共2 000 张图像用于实验.每张图像都通过统一的人脸部位裁剪并调整至64 像素×64 像素的灰度图像.选取其中每个人前10 张共1 000 张图像作为训练样本,其余为测试样本.图6 为其中1 人的训练样本和测试样本示例,图7 为本节实验的测试结果. 图6 PubFig 中1 人的训练样本和测试样本示例图Fig.6 Sample images for one person from PubFig face database 图7 中SMED1 代表SMED11算法,SMED2代表SMED1/21算法,SMED3 代表SMED3/22算法.由图7 可知,CESR 对PubFig 数据库的识别效果最差,这是因为它忽视了图像中噪声的空间结构,对比来说,SMED 很好地利用了空间结构所提供的信息,其中,SMED11取得了最优的识别率,即对于非限制场景下的人脸图像来说,属于特例的凸函数模型求解表现突出.此外,由于PubFig 中包含的是非限制场景下的人脸图像,这使得抗噪性强的RRC算法因为训练样本数据的不稳定性,不能有效揭示测试样本数据间的差异而影响识别性能,其识别结果仅略高于CRC.而对于它取得了44.3%的有竞争力的识别结果,略高于SMED1/21算法.综上所述,SMED 由于不需要过多地依赖训练样本数据之间的变化,而是通过考虑图像中噪声的内部结构,采用切合实际的分布来描述误差矩阵,故而能获得相对更佳的识别性能. 图7 PubFig 人脸库中不同算法的识别率对比Fig.7 Comparison of recognition rates on PubFig database 除识别性能外,运行效率是影响分类算法实际应用能力的另一关键指标.本节对AR、ExYaleB 和PubFig 数据库中的几种算法进行测试效率对比.表2 和表3 显示了各算法在不同数据库中单个样本的测试时间. 表2 为第4.2.1 节实验状态下的测试时间对比;表3 中ExYaleB 数据库里白色、黑色、baboon 和鲜花遮挡的测试时间均在60% 遮挡程度下获得.此外,所有数据都通过10 次实验运行并取平均值得到. 表2 AR 数据库中各算法测试时间对比(s)Table 2 Running time of competing algorithms on AR database(s) 结合表1 和表2 可知,CRC 在识别率上虽然与SRC、FFS 以及较为接近,但是其运行效率却远远优于这些算法,达到了ms 级的反应速度.以运行效率减弱为代价提升鉴别性能,从表2 可见其运行时间为CRC 的3 000 多倍,因此实用性欠佳.RRC 在光照影响、墨镜遮挡和围巾遮挡这三种情形下的识别率表现突出,接近SMED 的识别性能,但其在实现过程中需要迭代计算操作,因此运行率较低.最后,在AR 数据库中SMED 的运行效率高于RRC、FFS、和仅次于CRC和SRC,但其识别率却远高于CRC 和SRC.此外,结合表3、图5、图7 中各算法在ExYaleB、PubFig数据库中的表现可知,虽然的鉴别性能在大多数情况下接近于SMED 算法,但在大部分数据集中都需要消耗更多的运行时间,不适宜于实际的分类应用.而抗噪性不错的RRC 算法的运行时间却随数据集的不同浮动较大,稳定性不高.综合而言,SMED 由于采用迭代加权最小二乘法进行模型求解,能在很少的迭代次数下获得算法收敛,因此其综合运行效率领先于除CRC 和SRC 的其他对比算法.而且鉴于SMED 具有较高较稳定的识别性能,故而值得推广应用. 表3 ExYaleB、PubFig 数据库中各算法测试时间对比(s)Table 3 Running time of competing algorithms on ExYaleB,PubFig database(s) 本文提出一种联合平滑矩阵多变量椭圆分布的稀疏表示算法,该算法强调误差矩阵中各个像素间的依赖性并假定误差矩阵作为一个随机矩阵变量服从于矩阵多变量椭圆分布.由于通过上述假定构建的目标函数具有非光滑性,不利于问题的优化求解,故先引入辅助变量光滑模型,而后采用迭代加权最小二乘法优化求解模型.此外,文中对SMED算法的收敛性和复杂度进行了理论分析,并讨论了模型的参数敏感性.以人脸数据为例,采用AR、ExYaleB 和PubFig 数据库验证了所提算法的性能优于经典算法.综上所述,本文的创新点包括:1)采用矩阵多变量椭圆分布描述误差矩阵,增强算法抗噪性;2)引入辅助变量光滑模型,易于获得全局最优解,提升算法识别能力;3)采用迭代加权最小二乘法优化求解模型,加快算法收敛速度. 分析研究发现,所提算法SMED 虽然易于实现且性能卓越,但运行效率上仍受到限制,无法满足视频跟踪等在线应用系统的需求,且其与目前最先进算法的识别率仍有一定差距,后续工作有待进一步提升算法的识别精度.此外,SMED 是否适用于更加复杂的噪声特征样本和遮挡环境,且能否将该算法扩展应用于一般的现实噪声[46],也是后续有待进一步研究探索的问题.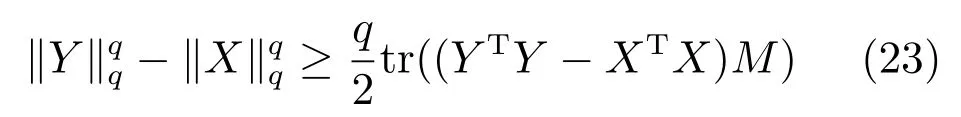
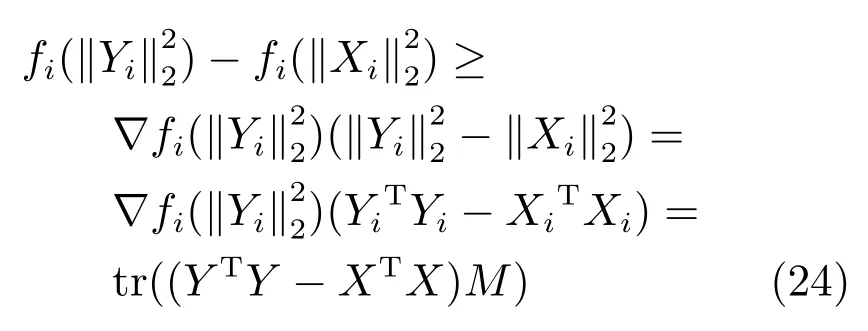
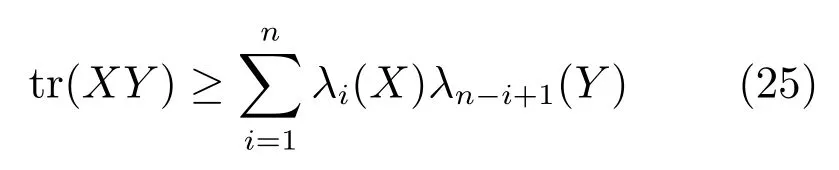
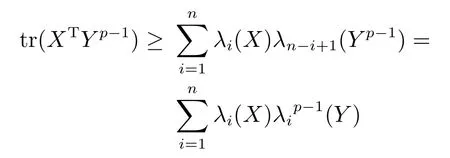
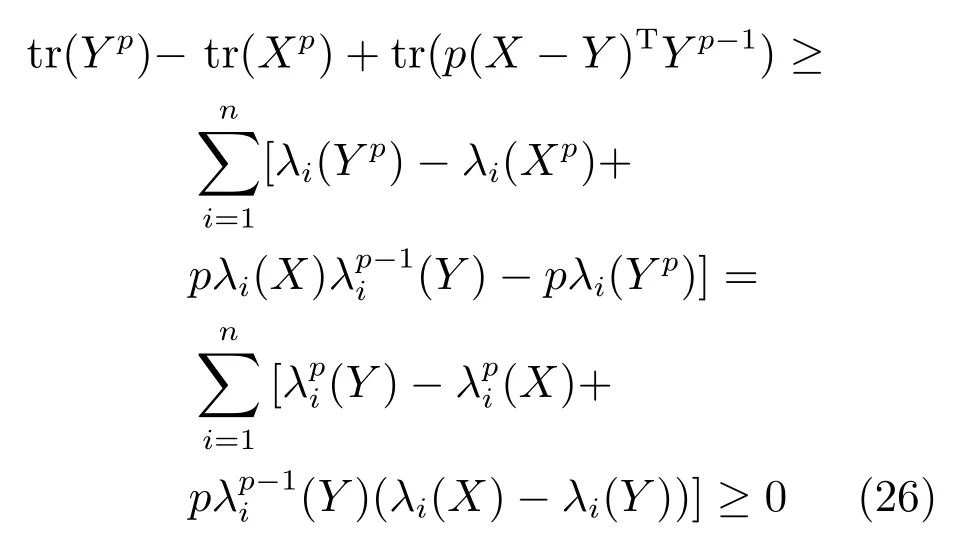
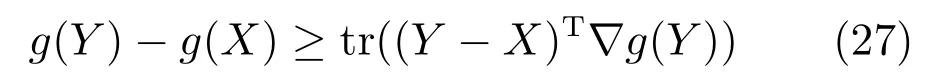
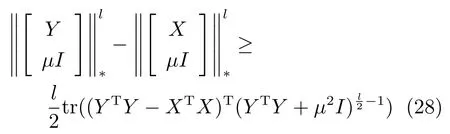
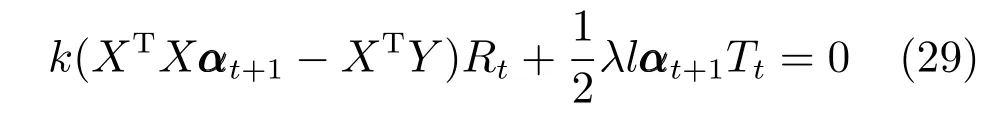
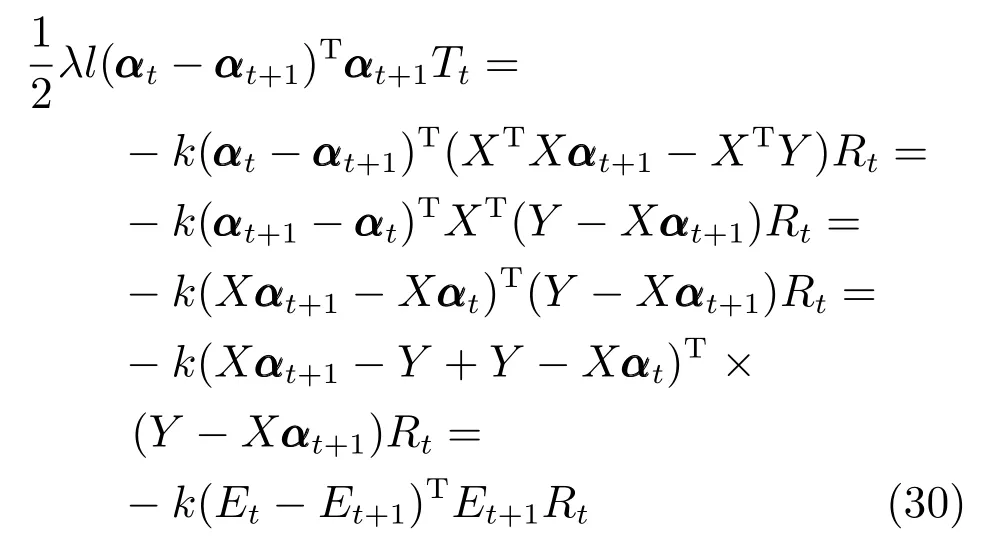
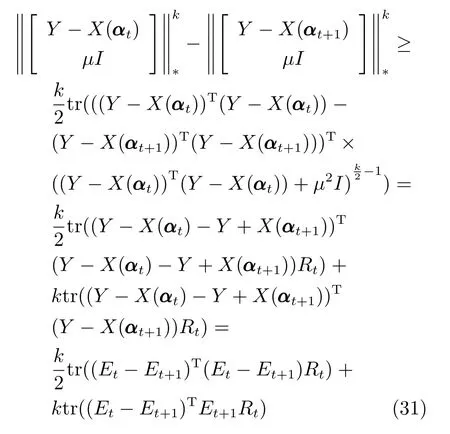
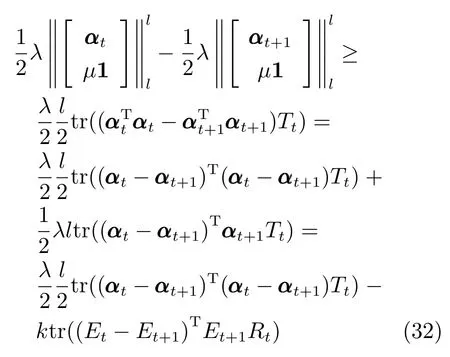
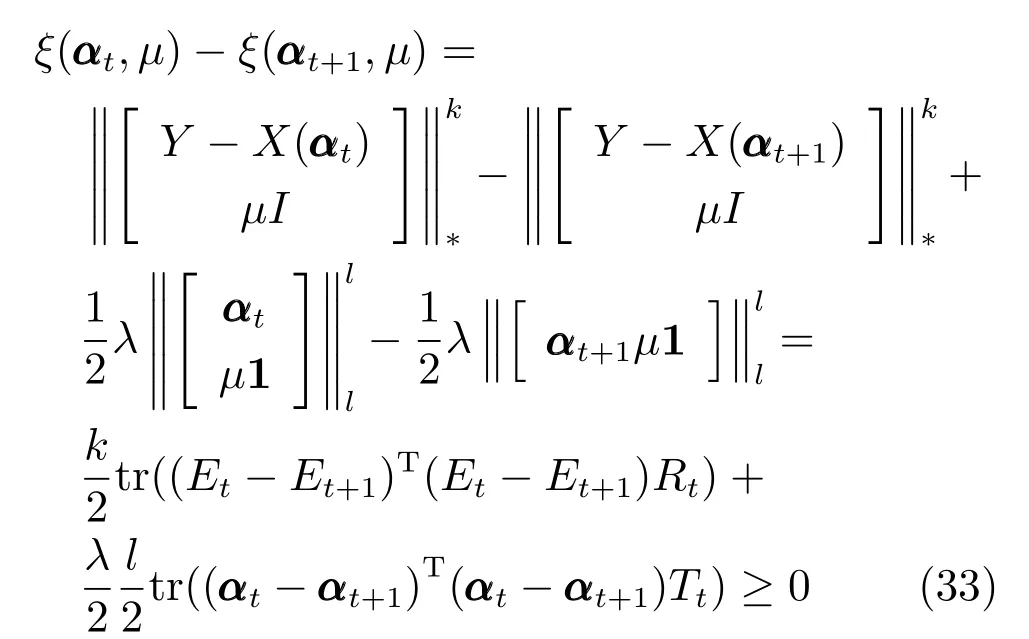
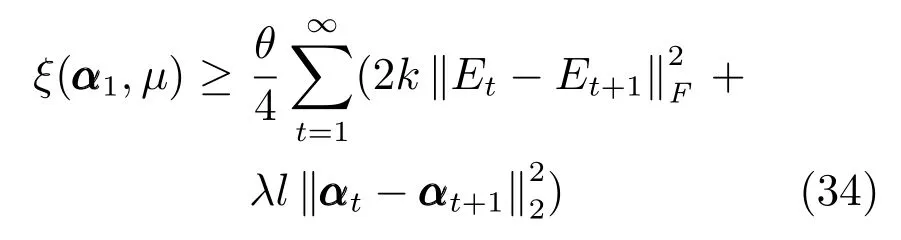
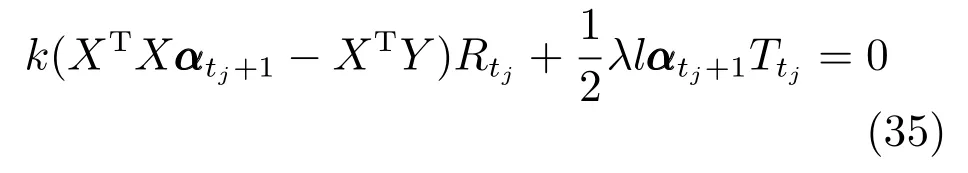
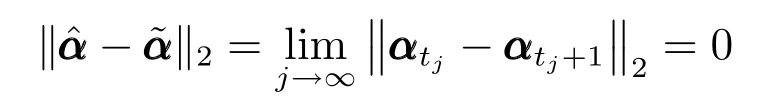
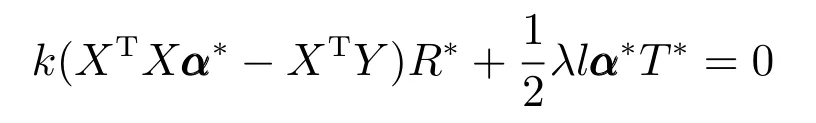
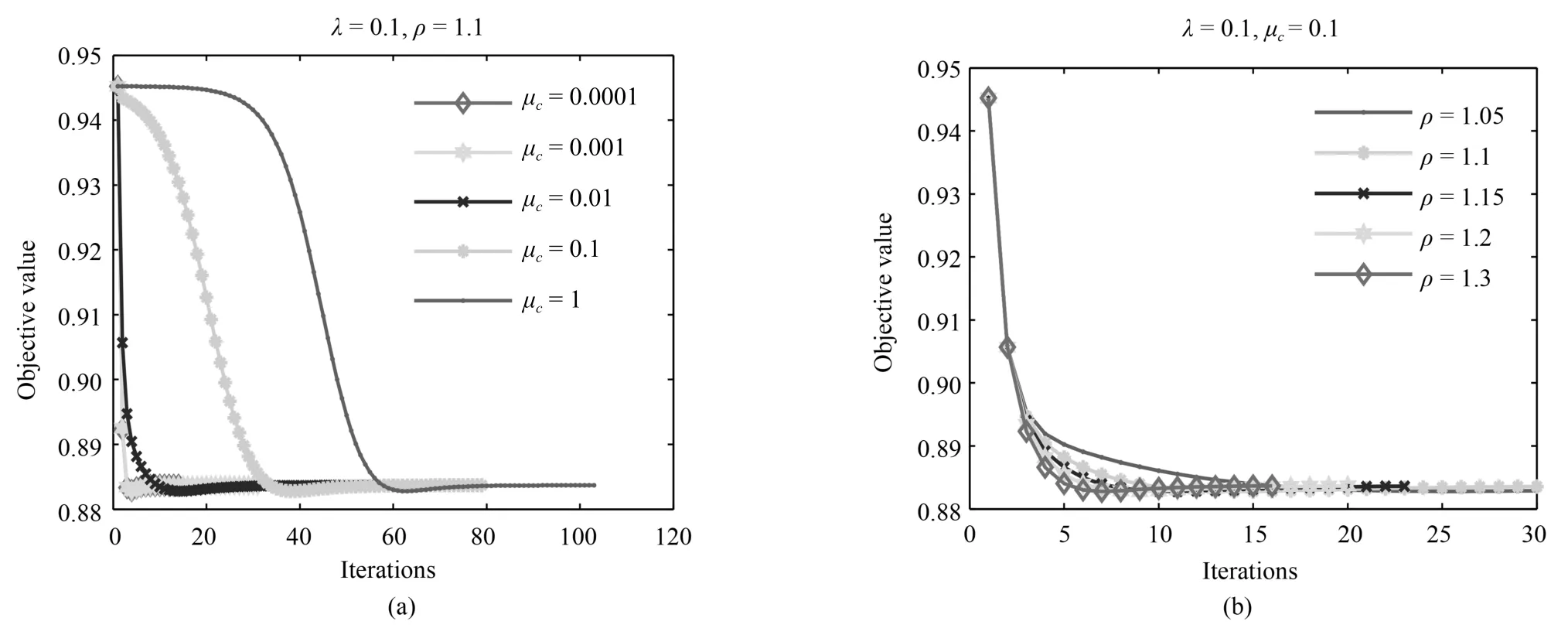
4 实验分析
4.1 人脸重构
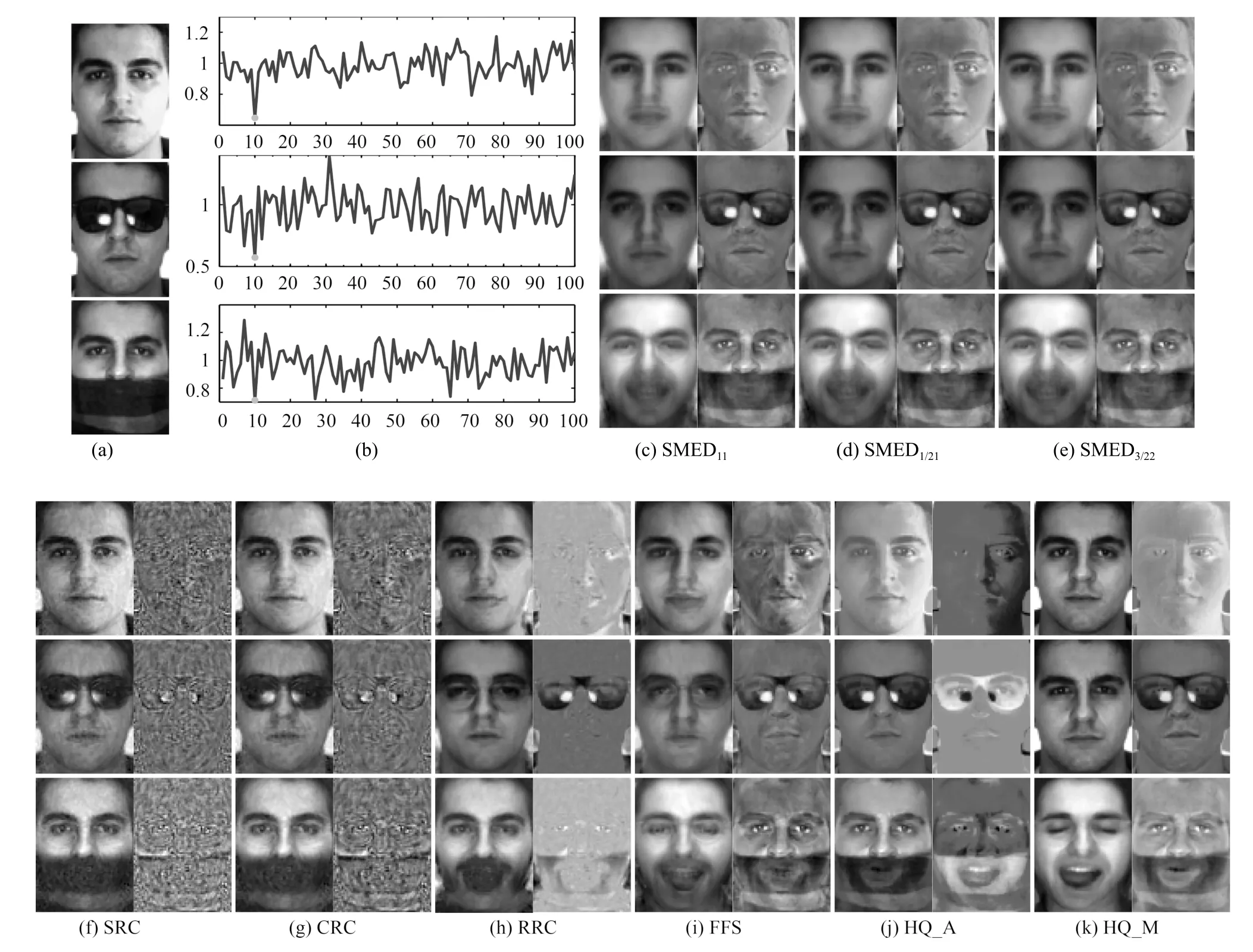
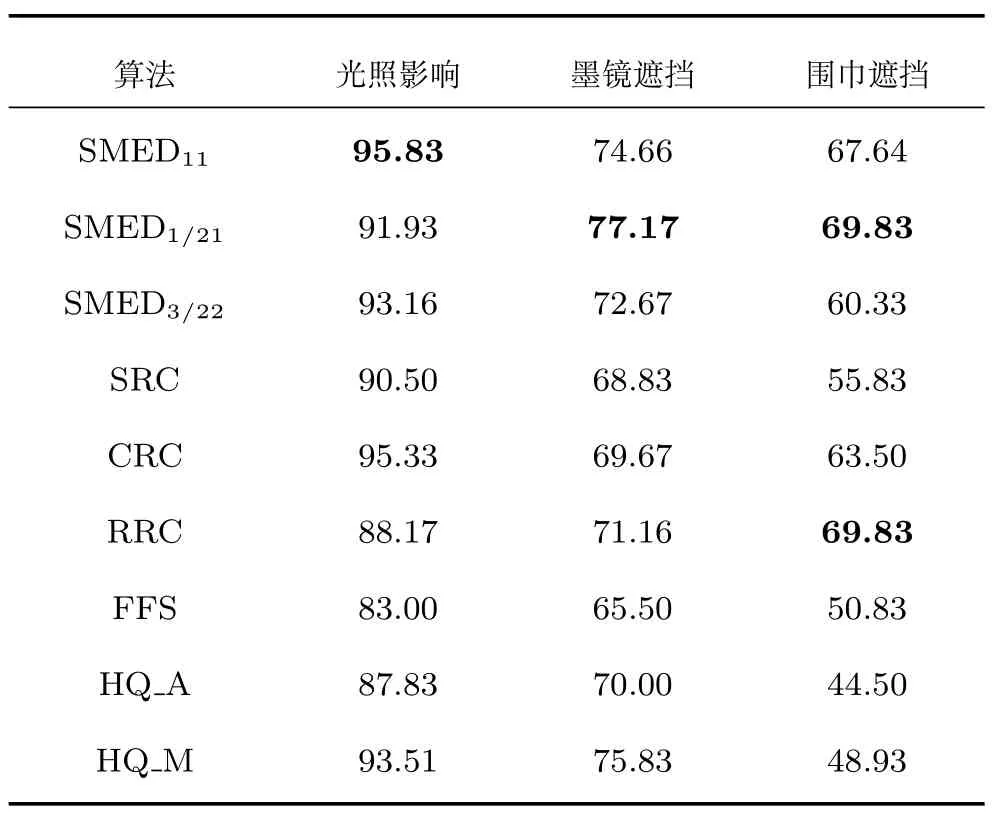
4.2 真实影响下的人脸识别
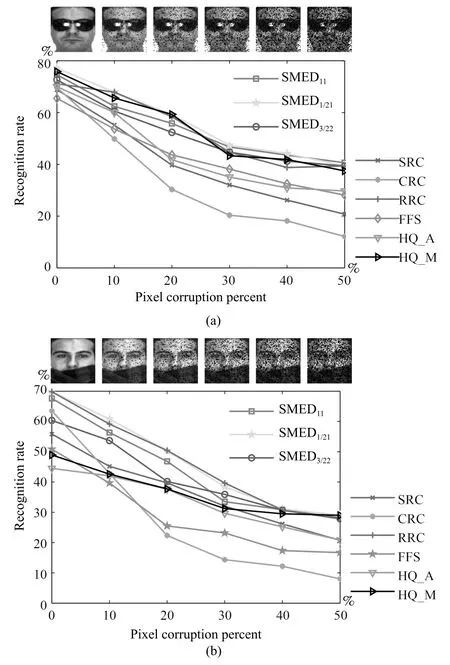
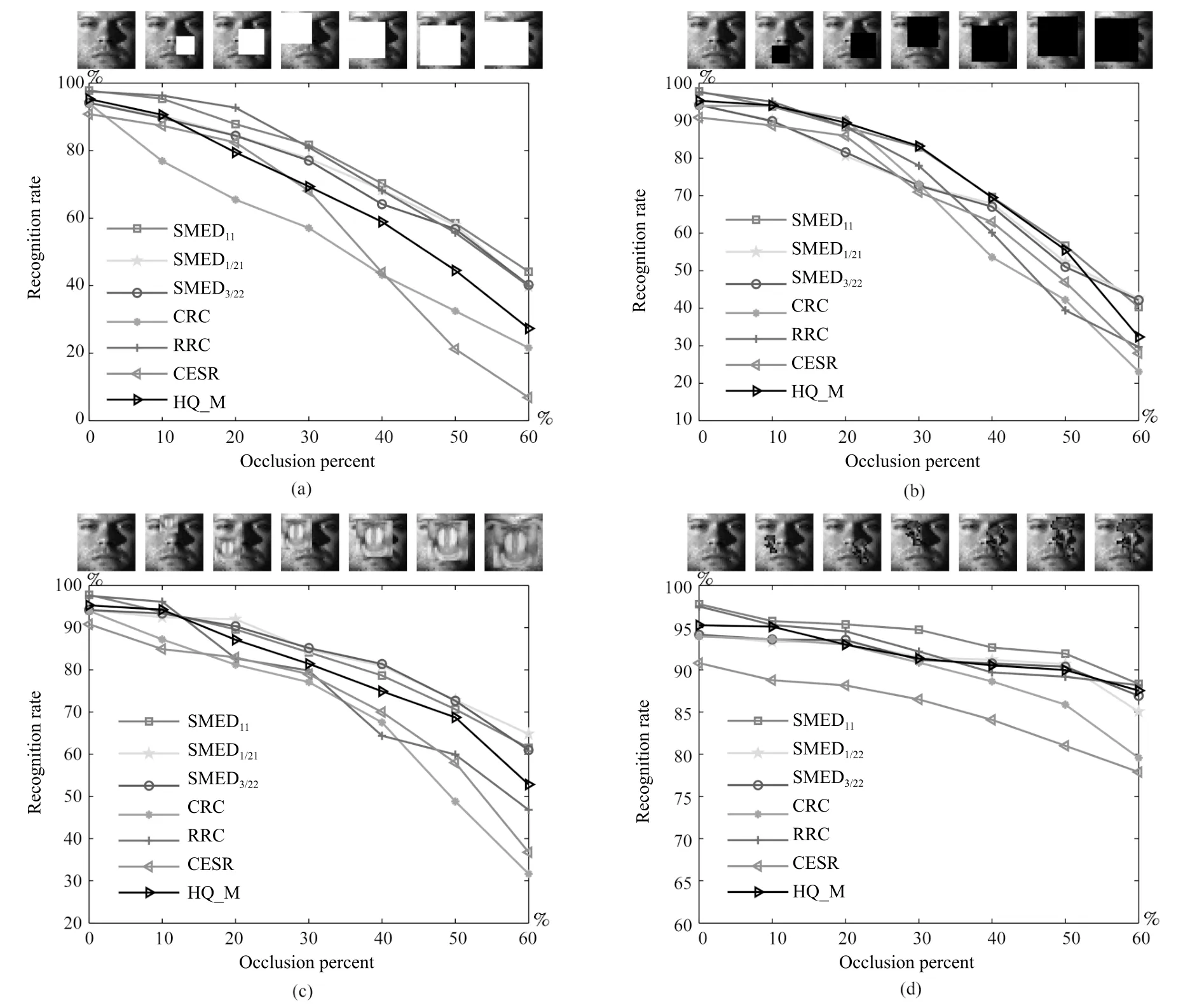
4.3 随机遮挡下的人脸识别
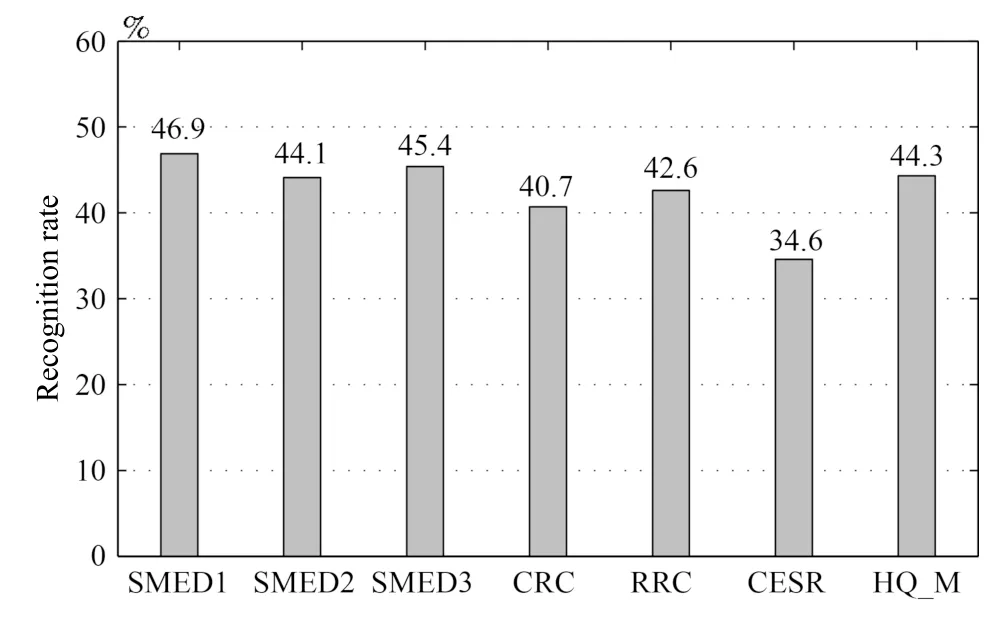
4.4 非限制场景下的人脸识别

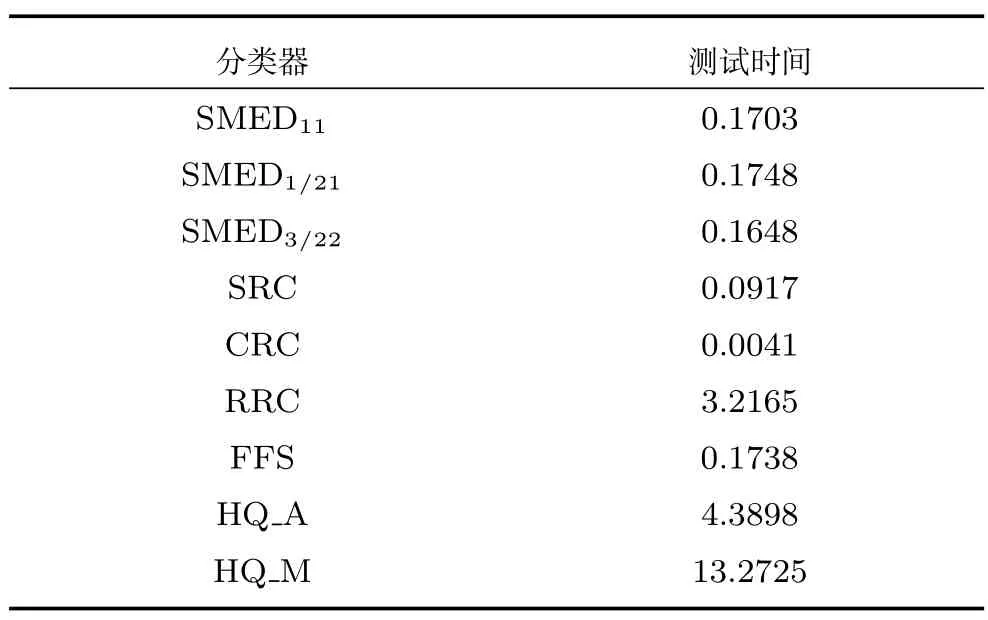
4.5 运行效率分析
5 结束语
