基于修剪策略的D-FNN 直接逆控制算法研究
2019-09-15张彩霞刘国文
张彩霞 刘国文
一个训练好的神经网络可以看成是一种知识的表达,与模糊系统中使用IF-THEN 规则表达局部知识不同,神经网络通过它的结构,更确切地说,通过它的连接权和局部处理单元,以一种分布式的或局部的方法来储存知识.神经网络中的前馈计算与模糊系统中的前向推理扮演同样的角色.这两种系统都能根据当前情况通过对存储知识的操作来执行任务,以得到期望输出.通过给定一个合适的行为来响应新情况是这两种系统的核心.但是,两者完成任务的方法是不同的.模糊系统是基于逻辑推论的插值推理,而神经网络是基于泛化能力的代数计算.模糊系统通常是从领域专家处获取知识,这个知识借助模糊逻辑理论融入系统.相反,神经网络通常从样本中获取知识,这个知识通过训练被吸收到神经网络中.模糊系统和神经网络的结合就形成了模糊神经网络,这种网络致力于两种方法的优点,同时避免它们各自的缺陷.把神经网络应用于模糊系统,可以解决模糊系统中提取模糊规则的问题,把模糊系统应用于神经网络,可以避免任意选择初值.
1 动态模糊神经网络理论分析
1.1 动态模糊神经网络的结构
本文提出的动态模糊神经网络(Dynamic fuzzy neural network,D-FNN)学习算法的特点是:不仅参数可以在学习过程中调整,同时,也可以自动确定模糊神经网络的结构.从功能上看,它等同于一个TSK(Takagi-Sugeno-Kang)模糊系统,该系统采用高斯隶属函数和T-范数乘积算子[1].
D-FNN 结构如图1 所示.

图1 D-FNN 示意图Fig.1 D-FNN schematic
在图1 中,x1,x2,···,xr是系统的输入数据,Y是系统的输出数据,MFru是隶属函数[2].
高斯函数表示的隶属函数为

其中,cij是xi的第j个高斯隶属函数的中心,σj是xi的第j个高斯隶属函数的宽度.
Nj为第j个节点的输出

总输出信号为

其中,y是输出信号,wk是模糊规则.对于TSK 模型[3]

TSK 模型

1.2 分级学习思想
D-FNN 的结构不仅由接收域决定,还由系统误差决定,尽管这两种方法都可以划分为分级自组织方法.由输出误差确定是否应该加入新模糊规则.
输出误差判断描述如下:(Xi,ti)是第i个输入数据,Xi表示第i个输入向量,ti表示第i个期望的输出,动态模糊神经网络输出为yi.
定义

如果

此时,增加一条新的模糊规则.ke值是根据动态模糊神经网络期望的精度预先选定的[4].分级学习主要思想能保证更简洁的结构和更短的学习时间.ke是个变量

这里,最大误差为emax,动态模糊神经网络的精度为emin,收敛常数是β(0<β <1)[5].
1.3 D-FNN 修剪技术
修剪策略采用的是误差下降率(Error reduction rate,ERR)方法.用ERR、SVD(Singular value decomposition)和ED(Eigenvalue decomposition)方法的不同的修剪策略将导致不同的DFNN 结构,即不同模糊规则数以及对于某个特定的性能,每条规则的参数不同.实验说明,ERR 方法具有明显的物理意义和稳定的数值计算,这就是该方法被广泛使用的原因.
T=(t1,t2,···,tn)∈Rn为系统理想输出,Y∈Rn为系统实际输出.Ψ∈R(r+1)u×n和T ∈Rn之间有如下关系[6]
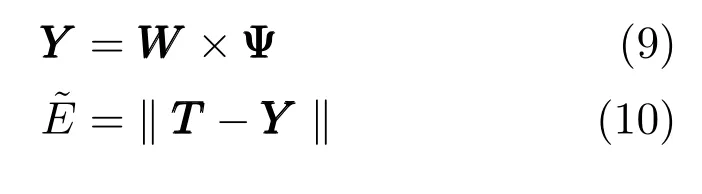

其中,期望输出为D=TT∈Rn,回归向量为H=ΨT=(h1···hv)∈Rn×v,v=u×(r+1),实参数为θ=WT∈Rn,误差向量为EEE ∈Rn,回归量为hi.回归量为qi,期望输出方差为误差下降率为
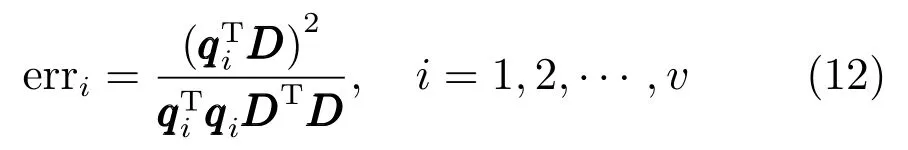
erri值如果很大,那么qi和D的相似程度就很大[8],qi对于输出结果影响显著.式(12)的几何意义也很显著.向量qi和D的夹角设为φi,那么
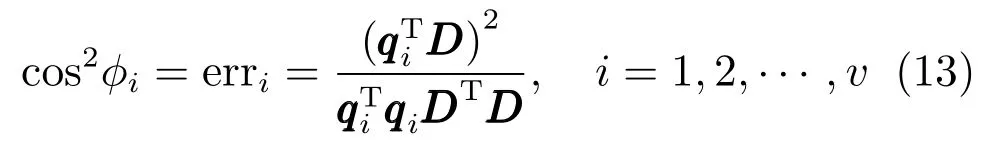
若φi=90◦,erri=0,表示两个向量正交,意味着qi对D无影响,如果,若φi=0,erri=1,意味着qi对D影响显著.∆=(δ1,δ2,···,δu)∈R(r+1)×u为erri(i=1,2,···,(r+1)u)重新排列的矩阵,∆的第i列δi是误差下降率[9].定义
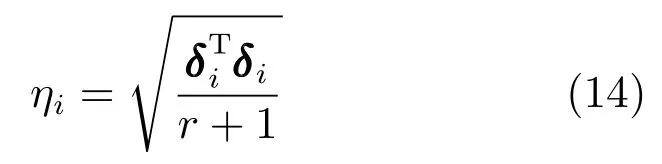
第i个模糊规则的重要性用ηi表达,值ηi越大,表示第i个模糊规则越重要[10].假设

预先设置阈值为kerr,则第i个模糊规则可以剔除[11].
未修剪时的训练误差总是比修剪后的误差小,但是经过修剪,无论是用ERR 还是SVD 或ED 方法,系统的测试误差(用RMSE(Root-mean-square error)来评判)总是小于未修剪的系统.
1.4 结果参数确定的分析
假定u个模糊规则是由n个观测数据产生的,可以写成式(16)N节点的模糊规则矩阵输出形式

Xj(x1j,x2j,···,xrj)是输入的观测数据,yi是系统的输出数据,可写成式(17)形式[12]

对于TSK 模型,W由下式给出

对于S 模型,WT∈Ru,Ψ∈Ru×n.

具有如下表达形式的W∗是属于最优的[13]

其中,Ψ 的转置为ΨT,Ψ 的广义逆为Ψ+=(ΨTΨ)−1ΨT.
卡尔曼滤波算法用于确定以下权值

其中,W0=0 和S0=χI为初始条件.经过i次迭代后的系数矩阵为Wi,第i个观测数据的误差协方差矩阵为Si,χ是一个正数,Ψ 的第i列为Ψi,u(r+1)×u(r+1)为单位矩阵I.
给予最新的数据最大的加权,而最旧数据加权最小,乃至被遗忘[14].其实现方法是加入一个遗忘因子λ.采用数据遗忘法的回归最小二乘法公式如下
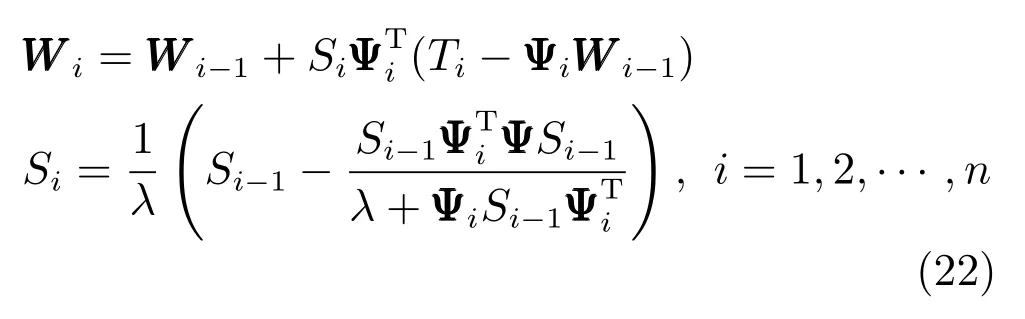
其中,0<λ<1,λ越小,表明数据遗忘越快.
当收集到的数据越来越多时,线性最小二乘法的自适应能力将会大大降低.在这种情况下,就需要减少旧数据的影响.
2 实验结果与分析
∆p是血压的变化,SNP(Sodium nitroprusside)是硝普钠,u为SNP 注射率,它们之间关系的传递函数为
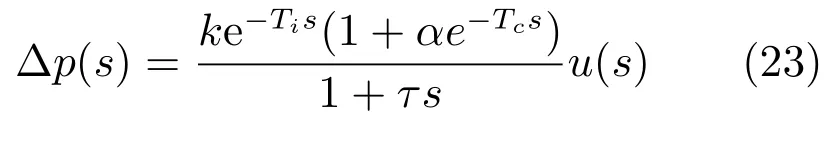
其中,循环延时为Tc,初始传送延时为Ti,硝普钠的敏感性表示为k,滞后时间常数为τ,循环系数为α.
根据式(23),在硝普钠影响下给出了平均动脉血压(Mean artery pressure,MAP)的离散数学模型
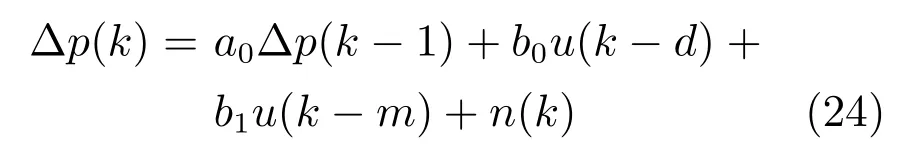
参数m,a0,b0,b1和d在采样时间下通过计算式(19)连续时间模型得到[15].
我们采用直接逆控制方法来检测D-FNN 能否逼近一个动态时变的系统.所谓直接逆控制法,就是基于系统的参考模型,模糊神经网络学习或逼近该模型的逆系统模型,并作为控制器与控制对象简单串接在一起,使合成的系统能够在期望响应r(t)和被控系统的输出y(t)之间形成一个一致的映射.D-FNN 作为直接逆控制方法的原理图如图2 所示.其中参考模型的作用是用来产生训练样本数据.
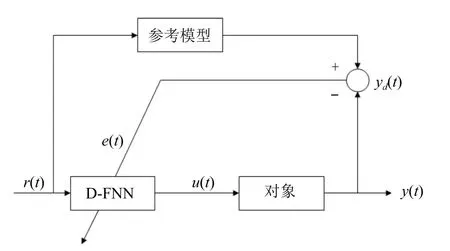
图2 控制方法数学模型Fig.2 Mathematical model of control method
在系统中D-FNN 作为控制器时,为了使输出值y(t)逼近期望值r(t),目标是要得到适当的控制行为u(t).这个仿真实验需要两个阶段即学习阶段与应用阶段.在学习阶段,D-FNN 辨识了潜伏在对象的时变动态逆模型.在应用阶段,D-FNN 作为控制器产生控制行为.
逆模型通常由带外输入的自回归非线性模型(Nonlinear auto regressive with exogenous input,NARX)经过简单的推导得到
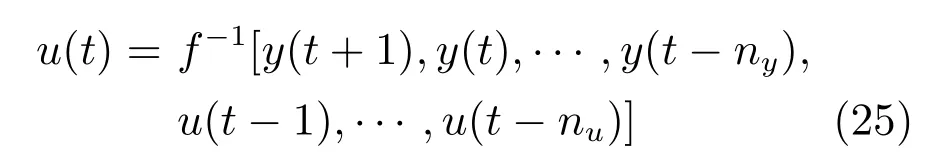
由式(25),可以看到计算u(t)的值需要知道y(t+1)的值,而y(t+1)是未来值.为了解决这个问题,一般情况下用r(t+1)代替y(t+1).由于r(t)与参考信号有关联,这个代替是合理的.
可以用NARX 模型直接构造如下的逆模型:u(t)=g[y(t+1),···,y(t−ny),u(t−1),···,u(t−nu)]
定义4 设[Tk1,Tk2],其中Tk1,Tk2∈T且1≤k1≤k2≤n,T为离散得分集,则称为离散区间得分变量。特别地,当k1=k2时,退化为得分变量。
取g≈f−1.实际上g不是f的准确逆模型,它只是数学上逼近这个逆映射.
在注射系统标准时不变模型与注射系统参数变化模型仿真研究中,通过对血压的控制来验证D-FNN 逼近能力及所提控制方案的有效性.
2.1 注射系统标准时不变模型
病人响应的数学模型表达如下:
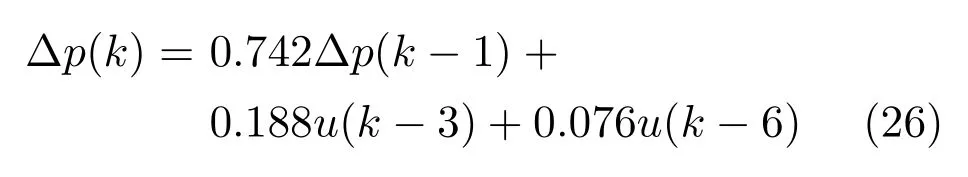
为了产生训练数据,药物注射率u(k)取为
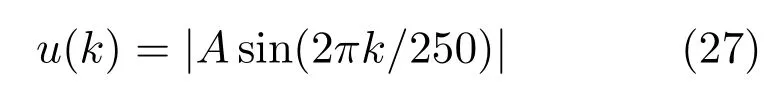
设A=50,初始条件为:当t≤0 时∆p(t)=0,u(t)=0,根据式(26)和式(27)提取200 个样本.式(26)的逆模型取为û(k)=f(∆p(k),∆p(k −3))其中,f是D-FNN,它代表式(22)的逆映射.DFNN 预定义的参数选择如下:dmin=2,dmax=35,emin=0.5,emax=50emin,β=σ0=35,k=2.5,kw=1.05,kerr=0.0007 训练结果如图3 所示.其中,图3(a)是训练阶段期望和实际注射的差别,图3(b)是训练阶段的均方根误差,图3(c)是训练阶段期望(-)和实际注射率(o)比较.
控制器采样间隔是15 s,高血压病人的血压设定为140 mmHg,D-FNN 控制器训练好后用于控制对象,最后病人的血压要求降低到100 mmHg,如图4 所示.其中,图4(a)可以看到血压随着硝普钠注射的变化而平稳地变化,并没有发生时延和震荡,这表明D-FNN 很好地学习了模型的特性,对系统进行了很好的建模.图4(b)是血压的实际的变化和期望的变化,期望的血压变化中含有方差为1 mmHg的白噪声,图4(c)是仿真结果的血压误差.修剪技术对于动态时变非线性系统的辨识是非常必要的,如果在学习进行时,检测到不活跃的模糊规则并加以剔除,则可获得更为紧凑的系统结构以及快速的学习速度.
仿真的结果如下:∆pmax=5.91;∆MAPmax=2.61;∆MAPmin=97.1.
由上述仿真结果可以看到:D-FNN 控制器能使得血压平稳的变化,能够满足实际的要求.
2.2 注射系统参数变化模型
根据式(26),得到了病人在SNP作用下,最大后验概率(Maximum a posteriori estimation)的离散数学模型

图3 标准时不变系统的训练结果Fig.3 Training results for standard time invariant systems
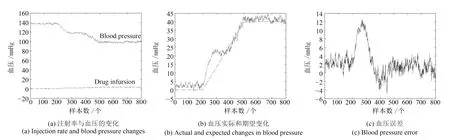
图4 D-FNN 对系统进行的仿真Fig.4 D-FNN simulation of the system
为了观察药物注射系统参数变化模型的时变特性,使用一个移动窗口.设置移动窗口的宽度w=120.其中药物注射系统变化模型的训练结果如图5 所示.图5(a)是D-FNN 控制器训练阶段的期望(+)和实际(o)输出比较,图5(b)是训练时均方根误差,图5(c)是训练阶段的输出误差.其中变化模型的测试结果见图6.图6(a)是药物注射率和血压之间的关系,图6(b)是D-FNN 控制器的实际与期望的血压变化比较,图6(c)是噪声环境下的药物注射率,其中扰动选择方差为1 mmHg 的白噪声.
表1 是文献[16]与D-FNN 中的仿真性能比较结果.IANC 方法与D-FNN 方法相比,D-FNN 的仿真结果(图6(a))非常理想,即使在扰动选择方差为1 mmHg 的白噪声环境下也没有大的延迟和振荡.用最大误差∆pmax来评估期望和实际MAP(平均动脉血压)变化的D-FNN 控制器的性能,IANC方法与D-FNN 方法相比较的结果列于表1 中.

表1 D-FNN 与IANC 的性能比较(mmHg)Table 1 Performance comparison between D-FNN and IANC(mmHg)
仿真时应注意到,移动窗的宽度w在辨识时变系统中有着重要的作用.宽度w较小时,会遗漏一些重要的数据;而宽度w较大时,收集到的样本数据越来越多,D-FNN 逐渐进入饱和而失去调整功能,使得时变参数无法辨识.
通过使用不同移动窗宽度,做了多次的仿真.根据RMSE(均方误差)和∆pmax进行评估D-FNN的性能,仿真结果表明,最优宽度w的范围是90≤宽度w≤110.
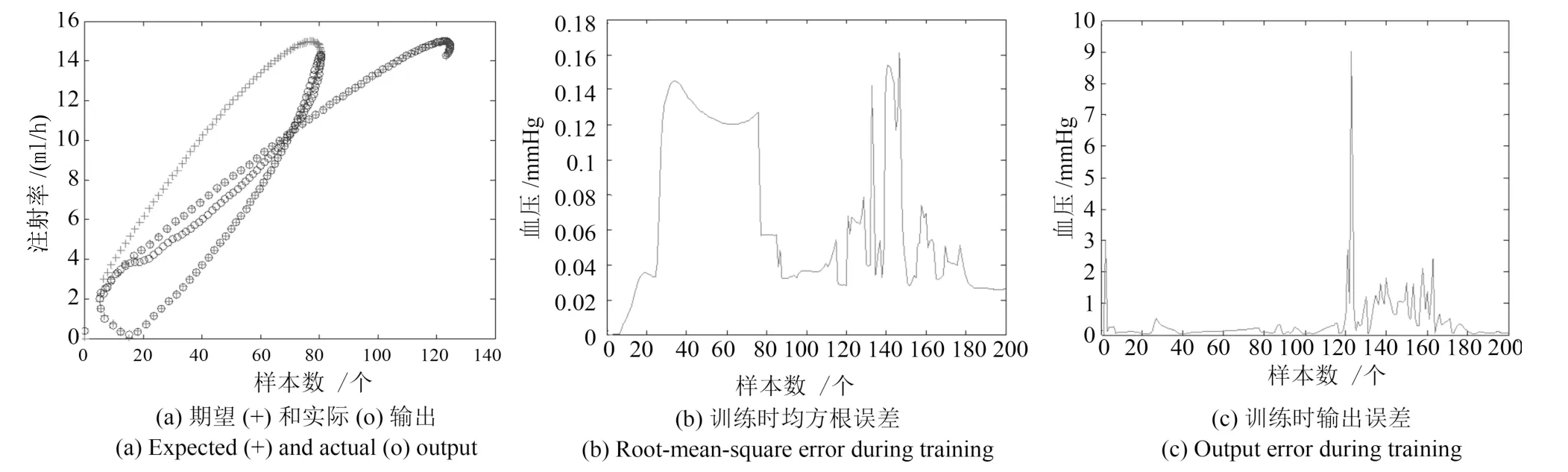
图5 参数变化模型的训练结果Fig.5 Training results of the parameter change model

图6 参数变化模型的训练结果Fig.6 Test result of parameter change model
从仿真结果来看,由于使用了修剪技术与移动窗技术,使得网络结构没有持续增长,可获得更为紧凑的D-FNN 结构,因而确保了系统的泛化能力.
3 结论
采用分级学习的思想能保证更简洁的结构和更短的学习时间,分级学习策略的一大好处是可以缓解学习过程中的震荡问题.实验结果表明,D-FNN控制器具有强大的在线学习能力,特别是当外部环境出现扰动时,D-FNN 具有很强的自适应性和鲁棒性可以把轨迹误差迅速地减少到接近零.D-FNN 可以根据对控制系统的重要性及系统的复杂性自动地产生或者删除模糊规则,在线学习时模型不需要预先设定,可以从训练数据设置次序自适应地学习,从而补偿了非线性系统建模误差处理外部扰动.通过仿真研究,动态模糊神经网络将会在许多实时自动控制系统中得到应用.D-FNN 学习的快速性未来还有进一步改进的空间.
