三维单粒子态的双向受控隐形传态*

彭家寅

内江师范学院 数学与信息科学学院，四川 内江 641199

1 引言

在量子信息科学中，最具特色和最重要的概念之一就是量子纠缠。在过去的二十多年中，为执行包括经典信息和量子信息在内的各种量子任务，量子纠缠在许多领域得到了广泛的应用，比如量子隐形传态[1]、量子密集编码[2]、量子态制备[3]、量子信息集中[4]等。自从1993 年Bennett 等人[1]率先提出量子隐形传态以来，量子隐形传态就引起了人们广泛的关注，并在理论和实验方面的研究取得了很大进展[5-16]；诸如受控隐形传态[7-8]、量子秘密分享[9-10]、量子信息分裂[11-12]和量子算子分享[13-16]等量子隐形传态的拓展版也相继被报道。Huelga 等[17-18]讨论了用双向隐形传态（bidirectional controlled teleportation，BCT）去执行非局域量子门的可能性。受双向隐形传态和受控隐形传态的启发，Zha 和Li 等[19-20]引入了双向受控隐形传态。此后，利用五粒子态[21]、六粒子态[22-24]和七粒子态[25]为量子信道的双向受控隐形传态被报道，并且Shukla 等[26]还指出了双向受控隐形传态的应用。除文献[26]外，还没有报道过关于以非最大纠缠态为量子信道的双向受控隐形传态。尽管在许多量子任务中，最大纠缠态是首选的量子资源，但用最大纠缠资源来实现一个量子信息处理协议仅仅是一个理想的愿望。在噪声环境中，粒子的存储和传输过程中存在退相干现象，纠缠的质量很容易退化，纠缠的数量会迅速减少。因此，不同用户分享的纠缠态通常为非最大纠缠态。由于特定量子任务，高维量子态的应用被研究[27-32]。当然，也包括使用三维纠缠来解决各种相关的量子问题[31]。如果采用三维最大或非最大纠缠态作为量子信道，能否执行双向受控隐形传态呢？为此，本文以两个广义三维最大纠缠GHZ 态为信道，研究三维单粒子态双向受控隐形传态问题，并将之推广到非最大纠缠信道的情形。借助投影测量和正算子值测量，分别提出两个推广方案。在这些方案中，空间分离的两方在遥远的第三方的监控下，以一定的概率同时交换他们任意未知三维单粒子态。

2 基于最大纠缠信道的BCT协议

假定Alice、Bob 和Charlie 是三个合法的使用者。Alice拥有一个任意未知三维单粒子态：

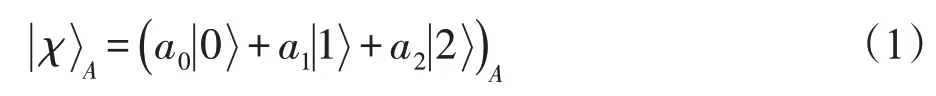
其中，复系数a0、a1和a2满足，而Bob拥有一个任意未知三维单粒子态：

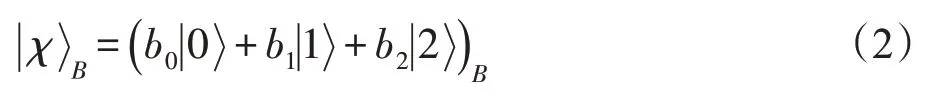
其中，复系数b0、b1和b2满足。Alice 想要把三维粒子A的任意未知态转给Bob，同时Bob也打算把三维粒子B的任意未知态转给Alice，并且要求在第三方Charlie 的许可下安全地进行，否则无法完成。当然，控制者不必知道的任何信息，但他对任务的完成起着至关重要的作用。

连接Alice、Bob 和Charlie 这三方的量子信道是如下两个被预先分享的广义GHZ态：

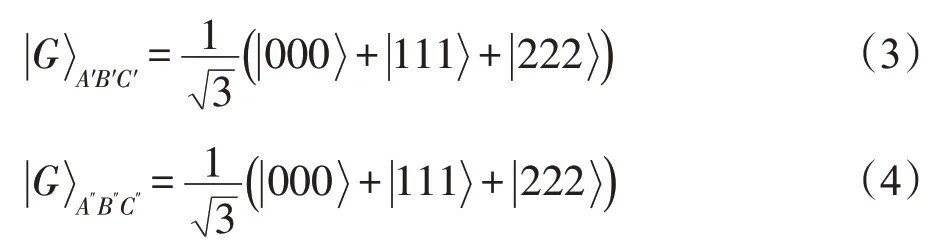
其中，三维粒子对(A′,A″)属于Alice，(B′,B″)属于Bob，而(C′,C″)属于Charlie。所有三维八粒子系统的初始态为：

本文的协议由如下连续的三步构成。

（1）Alice 和Bob 独立地执行如下操作，Alice 用广义Bell-态集：

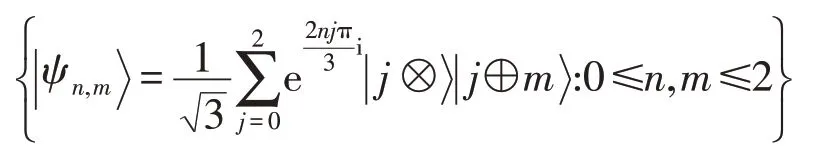
作为测量基去测量三维粒子对(A,A′)（⊕为关于模3的加法）。同时，Bob 也用上述测量基去测量三维粒子对(B,B″)。显然，他们能以相同的概率获得81 种可能的联合测量结果之一，并且余下的三维粒子组(B′,C′,A″,C″)的量子态塌陷为下列81种可能态之一：

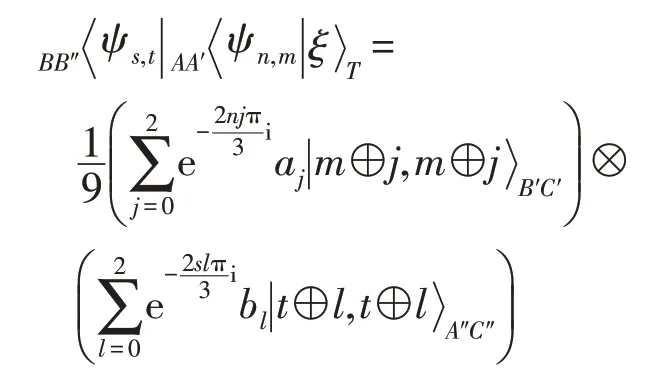
其中，n,m,s,t∈{0,1,2}。之后，Alice 和Bob 按预先的约定分别公布他们的测量结果。这里预先约定是指广义Bell 态分别对应经典三进制数对(n,m)和(s,t)，反之亦然。到此，Alice和Bob能否交换他们的量子信息还依赖控制者Charlie，因为上述塌陷态中仍含有粒子(C′,C″)，控制者Charlie 的作用将在下一步体现。

（2）如果监控者Charlie 允许Alice 和Bob 交换他们的量子信息，则他需要分别对粒子C′和C″施行三维单粒子测量，其正交测量基为：

Charlie测量后，粒子组(B′,C′,A″,C″)将以相同的概率坍塌为下列729种可能态之一：

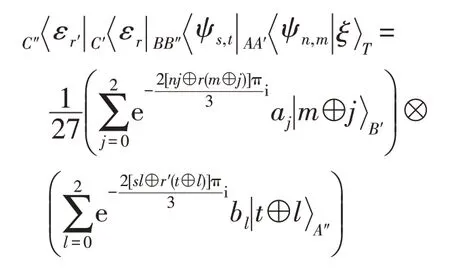
其中，r′,r,n,m,s,t∈{0,1,2}。预先约定三维单粒子态对于经典三进制数r，反之亦然。Charlie通过经典信道将测量结果r′和r分别告知Alice和Bob。从上面的等式可以看出，对于任何可能的测量结果集nmstrr′，三维粒子对(B′,A″)的量子态都是一个乘积态，但它还不是希望的形式。因此，最后一步需要Alice和Bob局部地重构目标态。

（3）Alice和Bob应分别对粒子A″和B′进行酉运算UA″和UB′，这两个酉变换可表示为：

那么，三维粒子A″和B′的态变成：

其中，r′,r,n,m,s,t∈{0,1,2}。这样，三维单粒子态的双向受控隐形传态被成功完成，并且成功为1，因此本文的方案是确定的。

注1在上述方案中，如果把Bob（Alice）和Charlie视为Alice（Bob）的两个代理商，那么Bob（Alice）和Charlie 中的任何一个都能重构Alice（Bob）的原始量子态，因此本文的方案可以修改为双向三维单粒子态分享方案。

3 基于非最大纠缠信道的BCT协议

本章在第2 章的基础上，考虑更一般的情形，即连接三个合法参与者Alice、Bob 和Charlie 的量子信道是如下两个广义的非最大纠缠GHZ态：

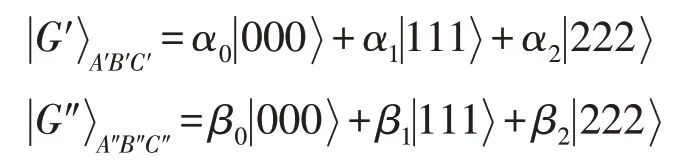
其中，系数αj和βj(j=0,1,2)为实数且满足归一化条件，其中三维粒子组(A,A′,A″)属于Alice，(B,B′,B″)属于Bob，而三维粒子对(C′,C″)属于Charlie。为了讨论方便，不妨假设现在，Alice和Bob希望在控制者Charlie 监控下，交换他们的三维单粒子态和三维八粒子的初始态可以写成如下形式：

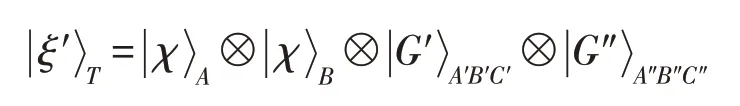
为了完成量子任务，Alice、Bob和Charlie需要执行与第2章中的（1）、（2）和（3）完全相同的操作，并公布他们的测量结果。这样，三维粒子A″和B′的态将变成下列729种可能态之一：

其中，r′,r,n,m,s,t∈{0,1,2}。

下面采用两种方法来交换他们的量子态，即重构他们的原始量子态。

3.1 采用投影测量的BCT协议

现在考虑用投影测量来执行BCT。为此，Bob对粒子对(B′,b)执行在基：

下的一个对角型分块酉变换：

其中：

同时，Alice 也对粒子对(A″,a)执行在基（9）下的一个分块酉变换（空白处表示0矩阵）：

在上述变换后，粒子组(A″,B′,a,b)的态变成：

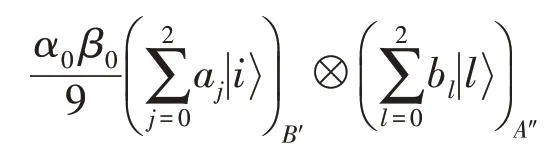
这表明双向受控隐形传态任务被完成。如果Alice和Bob的测量结果是其他情形，隐形传态失败。现在来计算方案成功的概率。归一化式（7）后知，获得测量结果集的概率是：

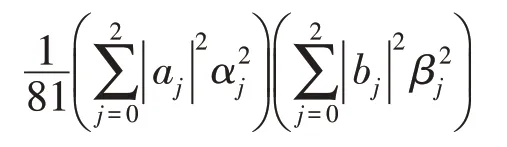
因此隐形传态成功的概率为：

对于其他联合Bell-态测量结果，类似的分析，可以得到完全相同的概率，因此本文方案成功的总概率为：

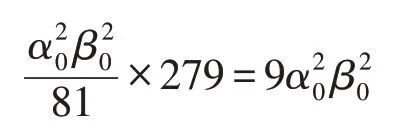
注2当时，本协议成功的概率为1，本方案退化为第2章的方案。换言之，本协议是第2章中协议的推广。

3.2 采用正定算子值测量的BCT协议

从第3.1 节知，酉矩阵U1和U2都是9×9 阶矩阵，这不利于直接实验实现。采用正定算子值测量（positive operator-valued measurement，POVM）所获得的方案较第3.1 节之方案更易实验实现。本节就考虑用POVM去代替投影测量来执行BCT任务。不失一般性，仍考虑式（8），其量子态可写成：

其中：

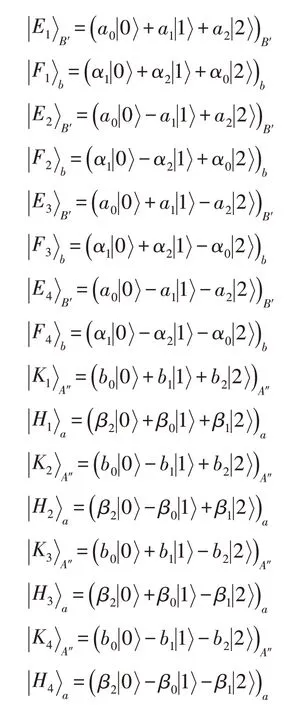
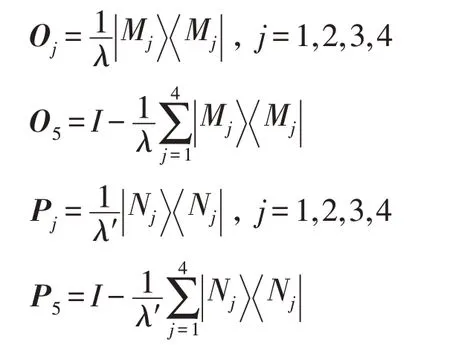
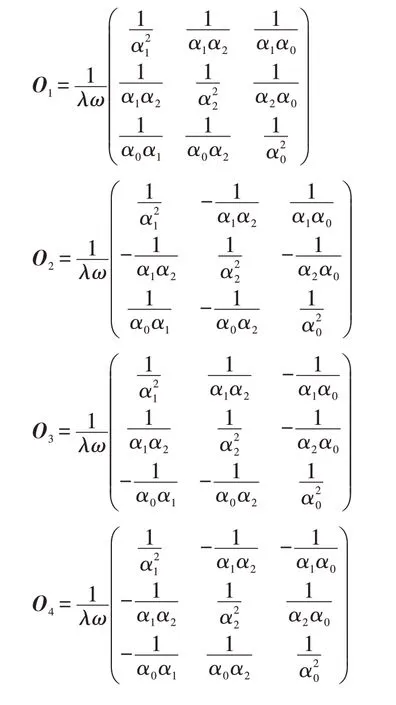
其中：

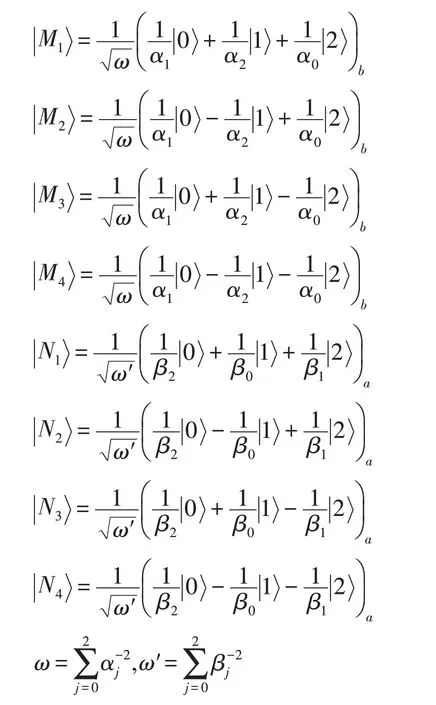
I为恒等算子，与αj(βj)相关参数λ(λ′)应确保O5(P5)为正定算子。为确定λ和λ′，算子O5和P5分别可以写成如下矩阵形式：

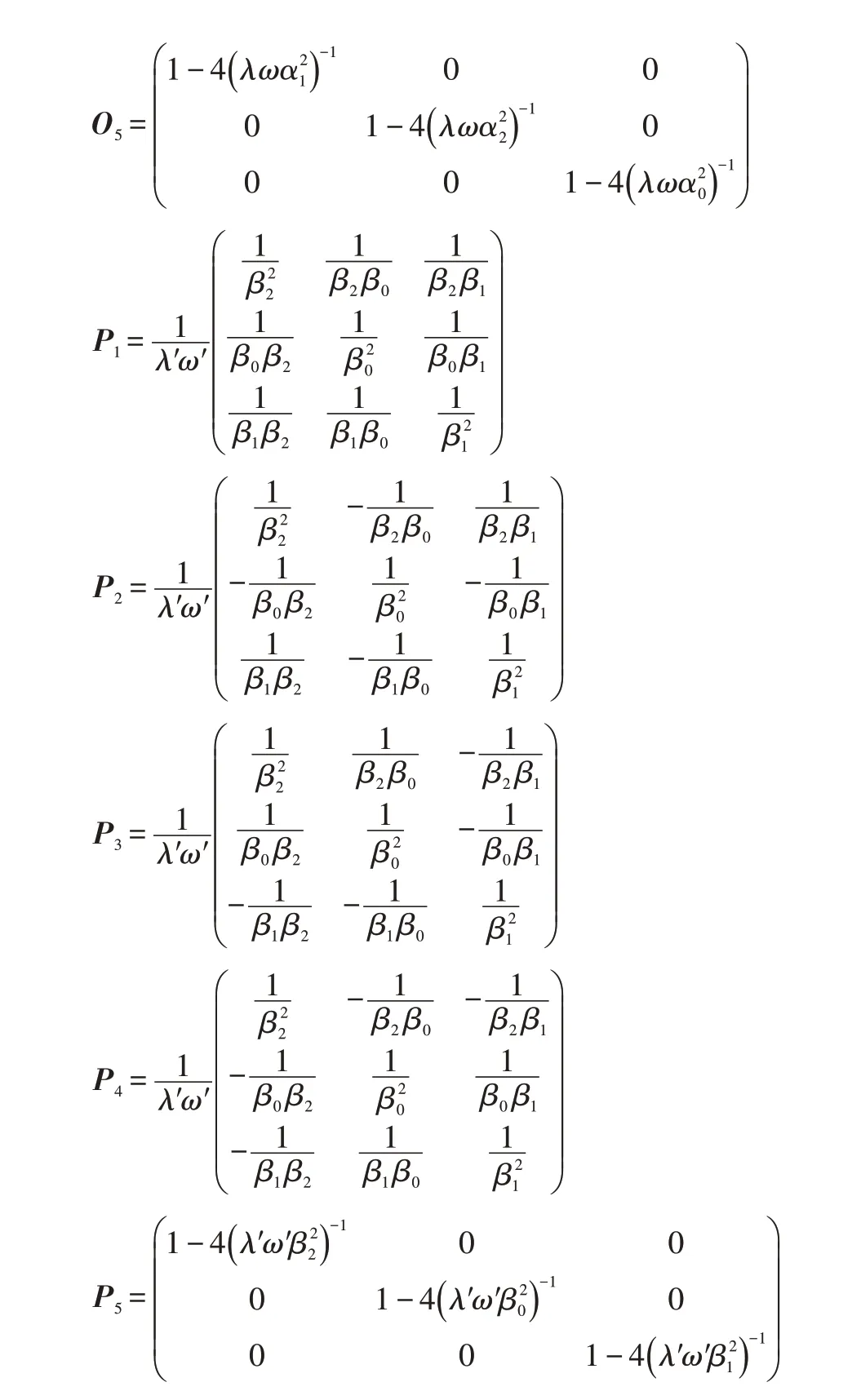
明显地，要使O5和P5都为正定的，参数λ和λ′应分别满足：

现在Bob对辅助粒子b执行POVM，定能以概率：

取得Oj，其中借助POVM值，Bob 推断出辅助粒子b的态。然而用概率他能得到O5，却不能推断出粒子b的态。他一旦获得，就意味着知道了，也就能成功重构Alice 的原始未知态。也就是说，如果Bob 得知，他就在中选择其一对粒子B′作用，就能以的概率获得Alice的原始量子态。类似地，Alice 按以Bob 相似的方式，也能以的概率得到Bob 的原始量子态。因此Alice 和Bob 能以的概率交换他们的原始量子态。

上面仅仅考虑了Alice、Bob 和Charlie 的联合测量结果是的情形。事实上，他们的联合测量结果共有729 种情况。对于其余的728 种情况，类似于前面的分析，Alice 和Bob 也都能以相同的概率交换他们的原始量子态。总之，本方案成功的总概率为：

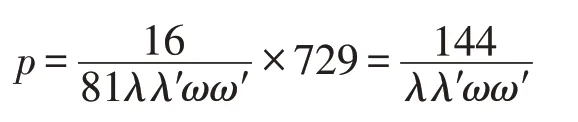
注3（1）容易验证，当，且时，也就是量子信道为两个广义最大纠缠GHZ态时，O5和P5为零矩阵，并且整个方案成功的概率为1。此时，本方案就变成第2章中的方案，即本方案是第2章中方案的推广。

（2）显然，所有的POVM 算子都是3×3 阶矩阵，而第3.1节中的U1和U2都是9×9 阶矩阵，因此本节的方案比第3.1节之方案更容易实验实现。

4 结论

最近，Zha等[19]讨论了利用五粒子团簇态纠缠作为量子信道的双向受控隐形传态。此后，双向受控隐形传态引起了人们浓厚的兴趣[20-26]，这些工作主要是以最大纠缠态作为量子信道的。然而，在现实的环境中，量子态通常是非最大纠缠态，并且在长距离通信网络中，BCT需要用到各种量子资源，包括高维态和非最大纠缠态，但目前却几乎没有这方面的报道。为此，本文考虑三维单粒子态的双向受控隐形传态。首先，以两个最大纠缠广义GHZ 态为信道来执行BCT 任务，推广了Zha 等[19]的方案，并且成功的概率为1。然后，用两个非最大纠缠广义GHZ态去取代先前的量子信道，借助投影测量和POVM，获得了两个三维单粒子的双向受控隐形传态协议，进一步推广了现有的方案。在本文的方案中，空间分离的两方在遥远的第三方的许可下，总能以一定的概率同时交换他们的三维单粒子态。当然，离开第三方的合作，BCT任务是失败的。同时，适当地修改本文的方案就可成为三维单粒子态双向分享协议。