连续负梯度方向获得共轭方向的六寻优化方法*

尹晓丽，孙 凤，李春明+

1.中国石油大学（华东）机电工程学院，山东 青岛 266580

2.中国石油大学（华东）中国石油大学胜利学院，山东 东营 257061

1 引言

优化方法逐渐形成了庞大的理论体系。目前，其主要研究方向多集中在群体智能[1]、聚类算法[2-3]、数据存储[4]等优化问题的研究。

上述算法属于基于其他理论的优化方法。经典的优化方法是针对可解析建模优化问题和可求或可测量目标函数优化问题而提出来的，包括一维优化方法、多维无约束优化方法、多维有约束优化方法、多目标优化方法和离散变量优化方法。在流场模拟[5]、车辆传动机构设计[6]、资源分配[7]、振动控制[8]等领域发挥着重要的作用。

经典的多维无约束优化方法在近几十年没有太大的发展。但是，在求解显式目标函数优化问题、可解析目标函数优化问题、大型稀疏系数矩阵线性方程组[9-10]等方面发挥着重要的作用。

负梯度方向因为其局部最速下降特性而成为许多优化方法的首选方向，比如坐标变换法、共轭方向法、共轭梯度法、由几何法获得共轭方向的算法[11]、优选可用方向法等。

共轭方向的构造方法有多种，比如：从不同初始点出发沿同一寻优方向获得的最优点连线是该寻优方向的共轭方向[12-13]。

在《优化方法》的教学实践和课题相关算法的研究探索当中，发现连续两次沿负梯度方向寻优，初始点与终止点连线符合上述共轭方向的构造特征，于是提出了三个算法。

2 共轭方向的证明

2.1 共轭寻优方向的定义与意义

在以设计变量为坐标轴所张成的设计空间当中，相互平行的矢量指同一寻优方向，任一矢量的正反向为同一寻优方向。在三维设计空间当中，两个寻优方向的最大夹角是90°。

对于一般N维二次目标函数：

沿方向s(0)寻优之后，如果令最优点（该方向上极小点的数值近似点）指向式（1）极值点的方向为s(1)，则s(0)和s(1)满足以下关系式：

称为s(0)和s(1)关于G共轭。这是新方向s(1)指向极值点的必要条件。从任意初始点出发，依次沿相互关于G共轭的寻优方向进行一维寻优，最多经过N次寻优即可找到极值点。对于二维的式（1），沿任一方向寻优之后，再沿其共轭方向寻优即可找到极值点。

2.2 两次同方向寻优获共轭方向的证明

设x(k)、x(k+1)为从不同点出发，沿方向s(j)进行一维寻优而得到的两个最优点。在该两点处，梯度方向g(k)、g(k+1)是目标函数等值面（线）的法线，而s(j)是该面（线）的切线，两者相互垂直，则s(j)和g(k)、g(k+1)之间存在以下关系：

根据式（1），有：

式（3）的两式相减，仍然等于0，即：

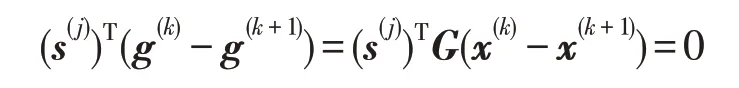
如图1所示，若取方向：

则s(k)和s(j)满足式（2）。

2.3 连续负梯度方向寻优获共轭方向的解释

从x(0)出发，沿目标函数的负梯度方向-g(0)寻优获得最优点x(1)，再从x(1)出发，沿负梯度方向-g(1)寻优获得最优点x(2)，则两个寻优方向分别为x(1)处目标函数等值面（线）的切线和法线，两者相互垂直。x(0)可视为从某点出发沿-g(1)寻优而获得的最优点。因此，根据2.2节，x(0)→x(2)是-g(1)的共轭方向，即：

2.4 连续负梯度方向寻优获共轭方向的证明

最优点的梯度方向与寻优方向相垂直，有：

对于多维一般目标函数，-g(0)和-g(2)不一定平行。根据式（1），x(0)与x(2)点处的梯度为：

g(0)=Gx(0)+b

g(2)=Gx(2)+b

两式相减，得：

上式左乘-g(1)。根据式（7）和式（8），等号左端为0。根据式（2）、式（6）所示方向s与-g(1)关于G共轭，或者说，s为-g(1)的共轭方向。

2.3 节和2.4 节从两个不同角度的分析是本文提出三寻法和六寻法的理论依据。

3 基于辅助方向的共轭方向法

根据2.2 节的证明，每次初始点和寻优方向确定之后，同时以寻优路线之外的某一辅助点为起点沿该寻优方向寻优，两次寻优的最优点连线作为下一次的寻优方向。该辅助点可以是当前点处负梯度方向上的一点。寻优方案（见图2）为：

（1）从x(0)出发，沿s寻得最优点x；

（2）在x点处的-g方向上适当取一点x(1)；

（3）从x(1)出发，沿s寻优获得x(2)；

（4）从x(2)出发，沿方向(x→x(2))寻得x(3)；

（5）如果x(3)满足终止条件，则结束寻优；

（6）令s为(x→x(2))，x(3)为x，转（2）。

Fig.2 Optimal scheme on negative gradient direction图2 基于负梯度方向的寻优方案图

对于一般目标函数的二维优化问题，上述算法相当于每轮两个相互共轭方向的共轭方向轮换法。对于式（1）所示的二维优化问题，每一轮的x→x(2)与s关于G共轭，即指向极值点。

4 基于负梯度方向的三寻法

对于以下二次二维无约束优化问题[11]：

沿负梯度方向的寻优过程如图3所示。由2.3节的分析和2.4 节的证明可知：x(0)→x(2)和x(1)→x(3)两个方向均指向优化问题的极值点，两者交点即为极值点。对于非二次目标函数，两者交点不一定为极值点，也不是任一方向上的最优点，用求交点的方法确定新点不科学。因此，连续沿负梯度方向进行三次寻优，从而获得两个共轭方向，以其交点作为新点的方法不宜采用。

Fig.3 Optimal process of negative gradient direction method图3 负梯度方向法的寻优过程

基于以上分析，提出基于负梯度方向的三寻法，其寻优方案为：

（1）从初始点x(0)出发，沿-g(0)寻优得x(1)；

（2）从x(1)出发，沿-g(1)寻优得x(2)；

（3）从x(2)出发，沿x(0)→x(2)寻优得x(3)；

（4）如果x(3)满足终止条件，则结束寻优；否则令x(3)为x(0)，转（1）。

5 基于负梯度方向的六寻法

对于多维优化问题，图3的两条共轭方向也不一定相交。沿两者的公垂线也不一定寻得较好的最优点。经第6章的算例验证，上述假设是正确的。

连续三次沿负梯度方向寻优所得两条共轭方向上的两个最优点又指示了一条新的寻优方向。利用该方向完善三寻法，即为六寻法。该六步寻优方案为：

（1）从初始点x(0)出发，沿-g(0)寻优得x(1)；

（2）从x(1)出发，沿-g(1)寻优得x(2)；

（3）从x(2)出发，沿-g(2)寻优得x(3)；

（4）从x(2)出发，沿s(3)=x(0)→x(2)得x(4)；

（5）从x(3)出发，沿s(4)=x(1)→x(3)得x(5)；

（6）从x(5)出发，沿s(5)=x(4)→x(5)得x(6)；

（7）如果x(6)满足终止条件，则结束寻优；否则令x(6)为x(0)，转（1）。

第（4）步s(3)上的点x可表示为：

其目标函数为步长α的一元函数。六寻法的程序流程如图4所示。

Fig.4 Program diagram of six search method图4 六寻法程序流程图

6 算例验证

6.1 一般二次三维优化问题

求解以下二次三维无约束优化问题：

目标函数的梯度为：

根据极值条件：

∇f(x)=0

该目标函数的极值点和极值为：

x*=[7.0 5.0 3.5]T

f(x*)=-20.75

二次目标函数的二阶偏导数矩阵为常数阵。该算例的二阶偏导数矩阵为：

正定，因此该点为极小点。

6.2 最佳寻优步长的解析解

当寻优起点x(k)和寻优方向s(k)确定后，以x(k)为坐标原点，以s(k)为正方向建立局部一维坐标系。由式（11），s(k)上点的目标函数值为：

式中：

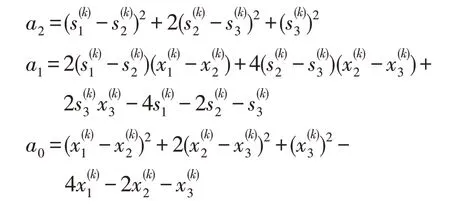
由极值条件：

可得最优步长为：

在s(k)上的最优点为：

6.3 寻优结果

取初始点为：

x(0)=[1 1 1]T

f(x(0))=-6

初始寻优步长取为0.1，终止条件值取为1.0×10-6。采用一维盲人探路法[14-15]获得寻优方向上的最优点。采用六寻法寻优，经12 轮，共72 次一维寻优

获得最优点和最优解为：

x=[7.000 0 5.000 0 3.500 0]T

f(x)=-20.75

采用负梯度方向法寻优，经101次寻优才获得该寻优结果。图5 为寻优过程，点线为负梯度方向法的，锯齿现象较严重，即越接近于极值点寻优效果越差；实线为六寻法的，共轭方向的寻优效率较大，两轮寻优即非常接近于极值点；虚线仅表示寻优方向；蓝色五角星为初始点和极值点。由于三寻法的寻优方向均包含在六寻法当中，从图5可见三寻法的寻优效果明显不如六寻法的好。可见本文提出的六寻法具有计算效率较大，寻优效果较好的特点。

Fig.5 Optimal process of example图5 算例的寻优过程

6.4 沿两共轭方向中垂线寻优的缺陷

在第一轮寻优当中，在第四和第五个方向（s(3)和s(4)）上任意两点之间的距离可表示为：

由极值条件：

可得方程组：

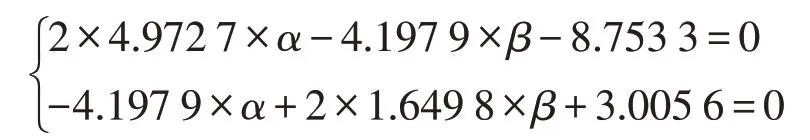
可求得：

α=1.070 5

β=0.451 0

对应于两条直线的公垂线垂足分别为：

x(α)=[3.252 1 1.751 5 1.248 7]T

x(β)=[3.125 1 2.242 7 0.914 3]T

相应的目标函数值分别为：

f(x(α))=-13.443 4

f(x(β))=-12.756 3

两者离第六次寻优所得的最优点较远，因此沿s(3)和s(4)公垂线寻优的效果较差。

6.5 Rosenbrock目标函数的寻优结果

将目标函数换为三维Rosenbrock 函数[16]。取初始点为：

x(0)=[-0.5 0.5 0.5]T

f(x(0))=15

采用负梯度方向法寻优，经过1 000 次一维寻优，调用目标函数34 762 次，锯齿现象极为严重，获得远离极值点的最优点：

x=[0.955 79 0.913 30 0.833 74]T

f(x)=9.491 1×10-3

采用六寻法寻优，经过448 次一维寻优，调用目标函数15 905次，获得最优点：

x=[0.999 93 0.999 86 0.999 72]T

f(x)=2.387 1×10-8

该复杂目标函数更加体现了六寻法的优势。

7 讨论

7.1 本文的研究范畴

任何寻求最优方案、最优参数的方法都称为优化方法。在优化方法理论体系当中，本文的研究属于多维有约束优化方法领域，对其他领域也有参考价值。

7.2 本文的理论意义

对于二维（N=2）二次目标函数的优化问题，沿一个方向寻优之后，再沿任何方法得到的共轭方向进行一维寻优，均是连续N次沿相互共轭的方向寻优，因此这些共轭方向均指向极值点。对于二维一般目标函数的优化问题，共轭方向也是有效的寻优方向。似乎共轭方向已经完成了优化方法的任务。

但是，对于N>2 的优化问题，所有方法得到的共轭方向不一定相同，其寻优效果必然有所差异。本文的研究在于探索有效的寻优方向。期间，进行了许多有效的探索。比如第3 章基于辅助方向的算法和第4章三寻法。作为阶段性研究成果，这些创新算法均可成文发表。但是，探索出六寻法之后，这些算法就显得黯然失色了，因此只作为本文的辅助内容出现。

7.3 先进性分析

优化算法在数学推导的基础上容易获得创新，比如本文的第3 章、第4 章两个算法。但是，只有经过算例的计算机程序验证才称得上是成功的创新。很多成功的创新因为没有程序验证而悄然消失。

本文提供了较完整的C语言计算机程序，研究结果的可重复性强。本文的计算没有依赖于优化计算软件，为难以由优化软件解决的特殊优化问题提供了工具。对优化方法学科的发展具有积极的推动意义。

8 结论

六寻法充分利用了共轭方向的优势，通俗易懂，算法简洁，程序实现容易，寻优效果好。算例证明了其有效性和实用性[17]。一般二次目标函数的计算量比负梯度方向法的减小28.70%，比Rosenbrock 目标函数的减小54.25%。

本文的算例经手算一轮之后，验证了一维盲人探路算法计算程序的正确性。同时检验了沿第四、第五寻优方向的公垂线寻优不能寻得较好最优点的假设。

附录（主要计算程序）：

目前许多研究领域的优化问题依赖于计算机软件，如Matlab 软件的优化工具箱、ANSYS 有限元分析软件、Solidworks建模软件的优化方法插件等。本文研究新的优化算法，必须进行计算机程序设计。采用可移植性和通用性都较强的C语言进行程序设计。

六寻法的计算子程序如下：