关注图形与几何领域教学,发展学生空间观念
2019-09-12林蕊馨
林蕊馨

摘 要:数学是研究数量关系和空间形式的科学,对于空间的探索是数学研究的重要的方面,对空间的认知需要空间观念作为保障。
关键词:转化;实物图形;元素
空间观念应是数学重要的核心素养之一,空间观念是学生在空间知觉的基础上形成起来的,是对物体方向、距离、大小以及形状的知觉,是客观世界空间形式在人脑中的表象。
那么,如何在课堂教学中培养并发展学生空间观念呢?下面谈谈我的一些具体做法。
一、沟通生活的联系,实现图形与物体的转化
(一)由实物到图形
如在教学角的初步认识时,首先让学生说一说生活中在哪见过角,唤起学生对角的生活经验认知,接着教师出示实物图片,让学生在这些图片中找角,随着学生找角,课件出示相应位置角的图形,使学生感受到角的抽象图形存在于具体的实物之中。最后去掉实物只剩下抽象的角的几何图形,这个过程使学生经历了由具体实物到抽象几何图形的转化,感受到角是由生活中具体实物中抽象出来的。
(二)由图形到实物
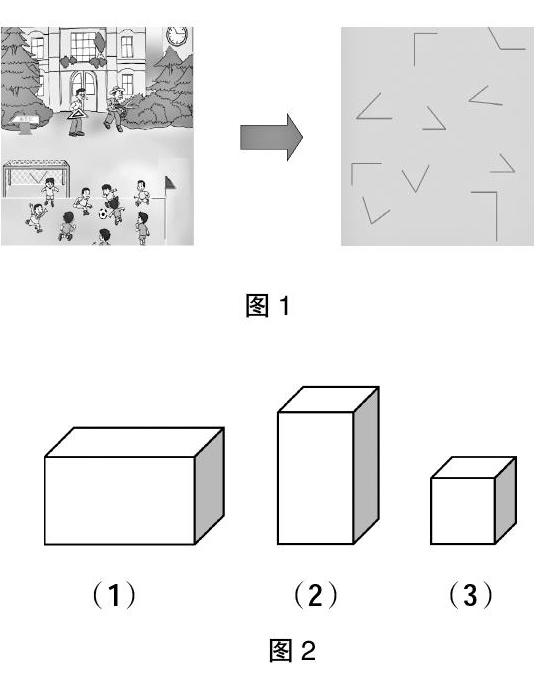
如在教学长、正方体的认识时,在学生初步認识了长、正方体的特征之后,可以进行这样的练习,出示几何图形(如图2),让学生借助几何图形找一找,生活中有哪些物体的形状与这些图形相对应。
借助图2(1),学生想到了多媒体的柜子、装水果的箱子等,借助图2(2),学生想到了音箱、茶叶盒等,借助图3(3),学生想到了魔方、药盒等生活中常见的实物。
二、分解基本要素,实现基本元素与图形之间的转化
(一)由图形分解基本要素
如在教学圆柱的认识这一内容时,我们发现学生经常出现综合应用特征解决问题时茫然不知所措的情况发生,问题出在哪儿?我们思考,每一种要素学生能够清晰地说出它们的特征,但是这些要素之间是否有联系,有着怎样的联系,这些联系与圆柱的特征是否有关系呢?综合全面地掌握要素之间的关系是对圆柱特征进一步刻画的重要环节,它能够让学生对圆柱特征的认识不是点状的、离散的,而是全面的、整体的、有联系的。因此,教学中,我们还可以在上面环节的基础上继续深入设计这样的环节:
圆柱的侧面展开图是长方形、正方形或者是平行四边形,有没有可能出现三角形、梯形?这是为什么?与圆柱的特征有什么关系?
问题引领学生进一步深入思考,结合圆柱的各元素特征综合考虑,建立起各元素之间的关系,因为圆柱的上下底面大小、形状完全相同,而且平行,因此侧面展开图的对边一定相等且平行,又因为圆柱的高处处相等,因此侧面展开图的高也都相等,这样的图形一定是长方形、正方形或者是平行四边形,如果剪开侧面时用了不规则的曲线,形成的图形也可能是异形,但是上面的两个特征依然存在。对元素之间的关系的深度思考引领学生进一步深入刻画图形特征,不仅对图形有了更加深入的认识,而且发展了空间观念。
(二)根据要素构建图形
如在教学长、正方体的认识时,我们可以提供给学生这样的两组学习材料:各种不同长度的小棒若干根、连接器若干个;各种不同大小的长、正方形纸片若干张、胶条。让学生任意选择一组学习材料制作长方体,并思考,通过制作长方体,对长方体有了哪些认识。这些学具材料是组成长方体的基本元素:连接器(顶点),小棒(棱),长、正方形纸片(面),学生会结合自己对长方体的基本认识选择并逐步调整学具完成长方体的制作,由基本元素构建立体图形,这个过程,也是学生对组成长方体基本元素属性及其关系逐步深入认识的过程,学生需要对元素之间的大小、长短、形状、位置关系等综合考量,将元素与心目中的长方体建立一一对应的关系,最终完成制作,可以说,这个过程,不只对长方体的基本特征认识的过程,也是发展空间观念的过程。
三、构建平面与立体的关系,实现二维与三维的转化
(一)由三维到二维
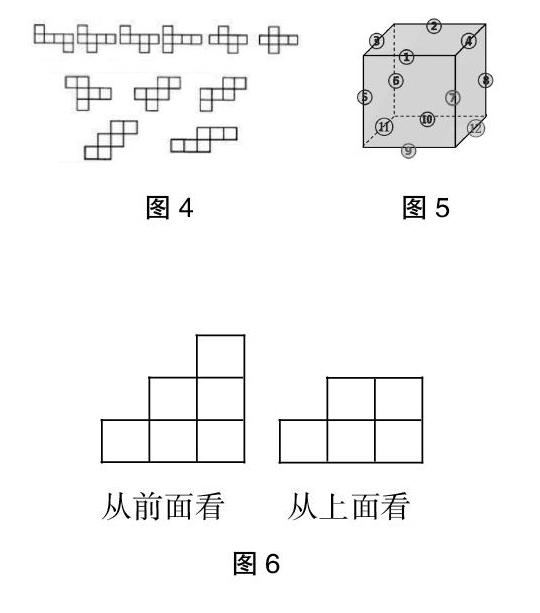
如在教学正方体的认识时,我们可以设计正方体的展开图的活动,首先可以让学生思考如果沿棱将正方体随意剪开,可以怎样剪,剪开后的平面图形是什么样子的,然后让学生动手操作,并反思对比想象中的图形与实际剪出的图形之间的不同,最后总结整理出11种展开图(图4),让学生观察展开图有什么特点?体会展开图与立体图形的关系。在此基础上,引领学生想象,如果这个正方体中的7、9、12 号棱不剪开(如图5所示),还能剪出正方体展开图吗?为什么?在学生想象的基础上再动手亲自做一做,感受到相交于同一顶点的三条棱如果不剪开,无法剪出展开图。
两次剪使学生经历了由三维向二维的解构过程,完成了由感性到理性的升华,学生的空间想象被推向了丰富、深刻的高层次阶段。
(二)由二维到三维
如在《观察物体》一课教学时,除了可以让学生能够依据立体图形画出不同位置看到的平面图形之外,还可以让学生依据不同位置看到的平面图形还原立体图形。教学中,可以设计这样的教学活动:如图,是由一些大小相同的小正方体拼搭而成的,依据这两个不同位置上看到的平面图形形状,想象出立体图形的样子,并把它拼搭出来。
学生依据两幅图示,建构起它们之间的联系,想象出立体图形实际构造,拼搭出立体模型,实现二维到三维的转化,在此过程中,使学生也感受到依据这两幅图拼搭出的立体模型并不是唯一的,进一步发展了学生的空间观念。
四、借助运动和变化,实现静态与动态之间的转化
(一)由静态到动态
图形与几何领域很多知识都是静止的,如果我们转化一下认知视角,让静态的知识元素动起来,能够丰富学生对知识的静态认知,发展空间想象力。
如在教学长方体的认识时,我们可以利用课件演示一个长方形面通过平移形成长方体的过程,然后引领学生站在面动成体的视角上审视长方体,将长方体与二维图形面建立联系,进一步印证长方体面棱顶点的特征,深化特征认识。
(二)由动态到静态
图形的运动和变化有时会让学生觉得事情很复杂,难以提取关键信息,抓不住问题本质,此时,我们也要转变一下认知视角,引领学生慢下来,用静态的眼光审视运动和变化,在运动和变化中捕捉静止的信息,发展空间想象能力。
如在教学平行四边形面积时,学生借助数方格想到了可以将平行四边形沿着高剪开,平移到另一侧,将平行四边形转化为一个长方形,通过平移运动的变化过程,学生实现了将一个新图形转化为学过的图形,此时,引领学生在运动变化中学会捕捉静止信息,用联系的眼光审视平行四边形与长方形,建立二者之间的联系,进而推导得出平行四边形面积计算公式,不仅解决了问题,也发展了学生的空间想象力。
总之,作为核心素养之一的空间观念的培养是小学数学教学的重要目标,作为教师,一定要关注图形与几何领域教学,抓住空间观念不同维度的表现,培养并发展学生的空间观念。
