面向两轮平衡机器人姿态检测系统的研究与设计

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

近些年来，在人工智能大火的背景下，机器人作为人工智能的一个研究领域也频频出现在人们的视线。机器人在一些危险、高难度的工业环境以及狭小空间的工业领域很快就得到了广泛应用。而且人们日常生活中的辅助机器人的工作环境也逐渐涉及到不平坦路面、斜坡、楼梯等复杂环境。因此在不同环境下保证机器人能够稳定地行走成为机器人完成任务的首要条件，在此背景下出现了两轮自平衡机器人。

根据两轮自平衡机器人姿态检测系统中的加速度计和陀螺仪的互补特性，对采集到的数据进行滤波和数据融合研究，并根据两者的互补特性进行了滤波算法设计。由于陀螺仪所测得角速度值只能短时间内处于稳定状态，这是由其本身特性所导致的；而加速度传感器测得的数据又存在很大的白噪声，在进行数据处理时通常会使用加权平均法和神经网络等方法。但是这些方法都存在一些缺陷，或是检测精度达不到要求，亦或是其模型和涉及的参数优化太过复杂不能适应本系统。因此在本系统中采用卡尔曼滤波算法，不仅要对陀螺仪的输出信号进行放大和滤波还要根据其互补特性设计卡尔曼滤波器。采用卡尔曼滤波器对两者的数据进行数据融合可以得出稳定和准确的数据，采用PID算法对车身的倾斜角度和驱动电机进行闭环控制。

1 系统总体设计

系统采用MC9S12X128作为姿态检测的主控制器，利用陀螺仪和加速度计对自平衡机器人的倾斜角度和角速度进行测量，包括陀螺仪的输出信号处理减少直接使用其输出力矩对检测精度的影响，以及利用卡尔曼滤波器对陀螺仪和加速度传感器的数据进行融合以得到更加准确稳定的角度和角速度值。然后通过PID控制算法对直流电机进行闭环控制。设计方案图如图1所示。

图1 整体设计方案

2 自平衡机器人平衡模型的建立

2.1 自平衡机器人的运动分析

两轮自平衡机器人通过车轮与地面接触，车轮和地面发生相对位移而上半部分由于惯性保持原来位置不动，从而造成身体倾斜。图2为通过轮子转动保持平衡的示意图。若保证机器人能够快速恢复到平衡状态，必须准确稳定地实时检测车身的平衡状态，将机器人身体倾斜产生的力矩通过控制车轮转动抵消，从而保持机器人平衡。

图2 轮子转动保持小车平衡

为了使机器人一直处于直立平衡状态，需要对模型运动学模型进行分析，从而建立可靠的数学模型。如图3所示，对机器人的运动姿态进行运动学分析时可以将机器人系统简化成一级倒立摆，而处于静止时的倒立摆是倒立摆模型分析的基础，因此应先对静止状态的一级倒立摆进行受力情况分析。

由一级倒立摆受力分析可以得出回复力的大小为

F=mgsinθ

(1)

在倒立摆的模型中由于其回复力的方向和偏离平衡状态的方向是一致的，因此不能像单摆那样回复到平衡的状态[1]。在系统中增加一种可使得回复力的方向与倒立摆的偏离方向相反的力以满足倒立摆可保持平衡的需要。

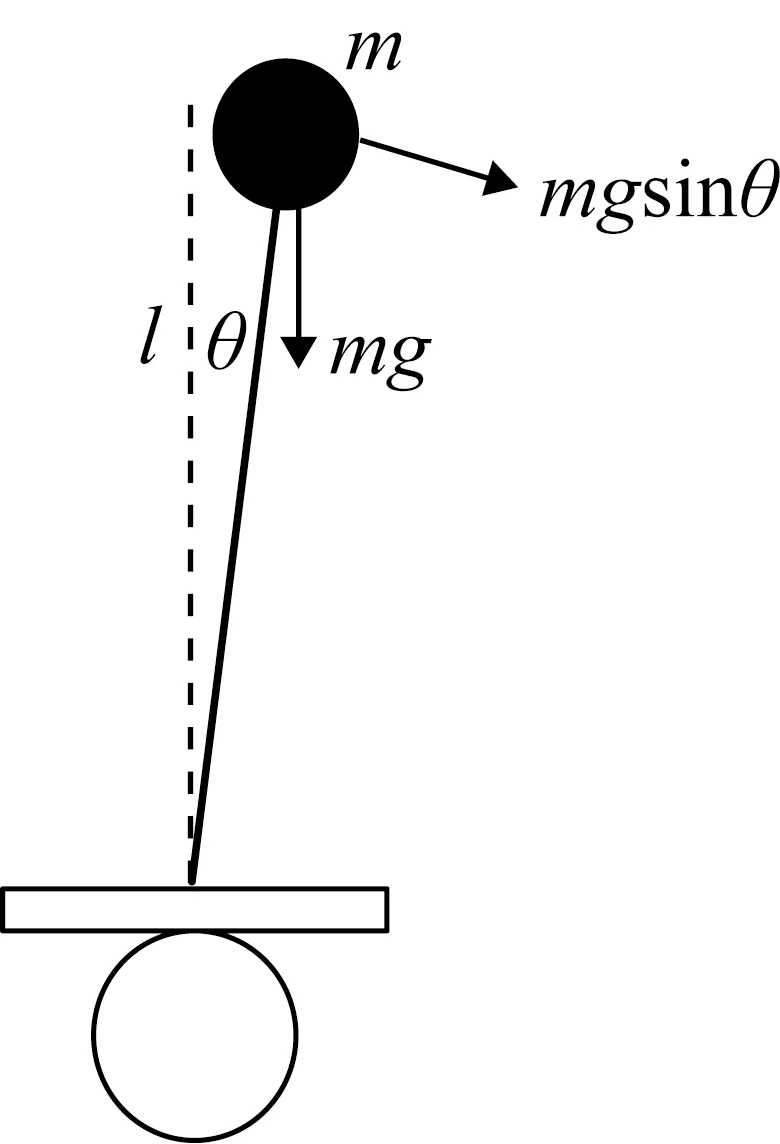
图3 一级倒立摆模型受力分析图

为得到一个与倾斜方向相反的合回复力，需要控制倒立摆下面的车轮做加速度运动。倒立摆在加速情况下的受力情况，如图4所示。

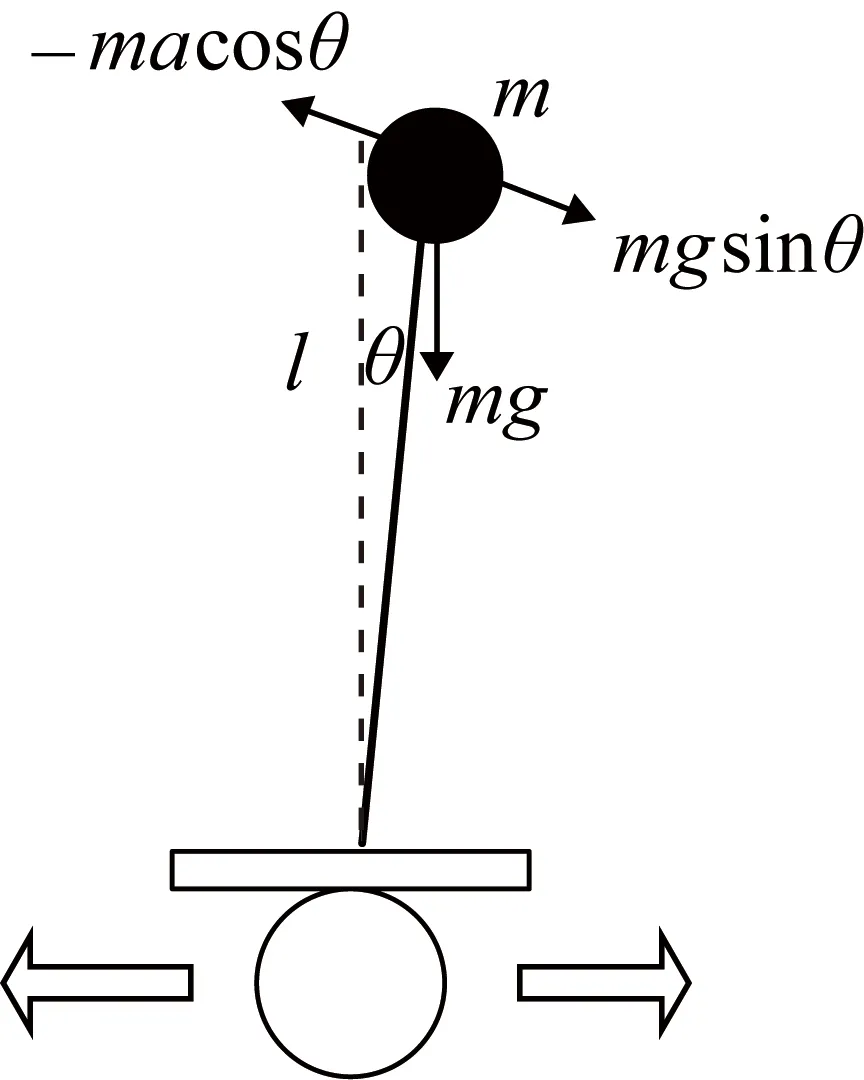
图4 非惯性系中的倒立摆受力分析

假定这种情况下的加速度为α。以地面作为参考系，根据牛顿力学可知倒立摆受到的惯性力为

Fg=macosθ

(2)

此情况下受到的合回复力为

F=mgsinθ-macosθ

(3)

在平衡机器人控制系统中，考虑到可控偏移角度θ值比较小的情况下可以对其进行线性化处理。当车身发生偏移时假设偏移角对机器人产生的加速度α与此时机器人姿态偏移角θ成正比，且二者之间的系数为k1，则式(3)可变换为

F=mgθ-mk1θ

(4)

当两者之间的比例系数大于重力加速度时，就能使合回复与倾斜方向相反。倒立摆在这种情况下可以回到平衡状态，但这个过程需要的时间比较长。因此需要在系统中增加阻尼力，阻尼力的大小应该与倾斜角度的大小成正比方向且与倾斜方向相反。因此可将式(4)变换为

F=mgθ-mk1θ-mk2θ′

(5)

根据上面的分析可以得出车轮加速度与倾斜角度之间的关系为

a=mk1θ+mk2θ′

(6)

式中，θ为倾角；θ′为倾角速度；k1、k2为比例系数。由式(6)可知，k1>g可以保证回复到平衡位置，而阻尼系数k2的大小则决定了倒立摆从倾斜状态回复到稳定状态的时间长短。

2.2 自平衡机器人的运动微分方程

在机器人高度l和质量m已知前提下，可以将自平衡机器人模型简化为放置于车轮上的倒立摆。假定车身在外界的干扰下产生了角加速度为x(t)的倾斜，对平衡机器人进行受力分析，得到车体倾角与车轮加速度为a(t)以及外力产生的加速度x(t)之间的运动方程。受力分析如图5所示。

图5 外力干扰条件下的受力分析

小车运动微分方程表达式为

(7)

当θ很小的时候有：cos(θ)≈1、sin(θ)≈θ，运动微分方程可简化为

(8)

自平衡车静止时a(t)=0,其运动微分方程为

(9)

2.3 PID控制器设计

由静止时运动方程(9)可以得出传递函数：

(10)

按照式(6)，角度θ和角速度θ′的反馈能够得到小车需要加速度值，因此引入θ及θ′之间的PD反馈环节在控制系统中，可得到加入反馈后的传递函数(式(11))和控制系统结构图，如图6所示。

图6 加入反馈后的控制系统结构图

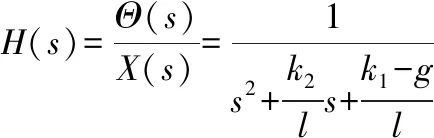
(11)

此时，系统的两个极点为

(12)

k1>g,k2>0时，两个极点都位于s平面的左半平面根据稳定判据系统稳定。因此，k1>g,k2>0时，小车可以保持平衡。

根据对控制系统的分析，系统中PID控制器的输出方程可写为

OUT_Motor=Kp·Angle+Kd·Angle_dot

(13)

式中，OUT_Motor为PID控制输出量；Angle为反馈倾角值；Angle_dot为反馈角速度值；Kp和Kd分别为比例系数和微分系数。

3 姿态检测系统

3.1 姿态检测的方式

自平衡机器人本身是一个不稳定非线性系统，因此在自平衡机器人维持稳定状态的过程中需要实时检测车身姿态。过程中需要对得出的数据进行整合，然后通过控制系统及时调整车身姿态来保持平衡。因此在机器人姿态检测时的精度和控制系统对车身姿态的调整速度对于系统的稳定运转至关重要。

根据平衡机器人自身特点和元器件特性采用MEMS加速度计和陀螺仪构成姿态检测系统[3]。虽然通过单独使用其中一种元件或者同时使用两种元件都可以测量出控制系统所需要的参数，但是由于器件本身的特性使得测出的数据中存在大量的噪声等缺陷。因此并不能将其输出的数据直接作为控制系统输入使用[4]。

利用示波器测得的陀螺仪与加速度计输出波形如图7所示。

图7 陀螺仪与加速度计输出波形

3.2 卡尔曼滤波数据融合

在相对简单的系统中对姿态的检测完全可以通过单一的传感器完成，但是精度受到器件本身特性的限制程度较大。单纯从改善硬件环境来换取精度上的可靠很难完成，并且随着系统使用时间的增加，单一器件输出数据的可靠性会越差。所以单一器件的姿态检测系统并不能完成自平衡机器人这种长时间姿态检测[5]。针对自平衡机器人对精度和反应速度有较高要求的系统，将使用两个传感器采集机器人姿态的数据并将其各自测得的数据先进行处理然后融合以获取更高精度的角度[6]。

由卡尔曼滤波原理可知，由前一状态的估计值和当前状态的观测值产生对状态变量的估计更新，从而得到当前状态的估计值，工作流程如图8所示。首先计算先验状态估计，再根据估计误差和卡尔曼增益矩阵，更新后验状态估计后，得出后验估计误差和协方差矩阵后，再次循环。

图8 工作流程图

卡尔曼滤波器解决离散时间控制系统的一般方法。假设卡尔曼滤波在k时刻真实状态是从前一时刻k-1的状态推算出来的，即

xk=Axk-1+Buk+wk

(14)

式中，xk为k时刻的状态；A为k-1时刻状态变换模型；B为作用在控制器向量uk上的输入控制模型；wk为过程中的噪声，假设其均值为零，协方差矩阵Qk符合多元正态分布，即wk～N(0,Qk)，且k时刻xk与zk满足：

zk=Hkxk+vk

(15)

式中，Hk为将真实控制映射为观测空间的观测模型；vk为观测噪声，且vk=0，协方差矩阵Rk满足正态分布：

vk～N(0,Rk)

(16)

卡尔曼滤波器的预估与更新[7]迭代过程如下，每个公式都假设初始状态以及每一时刻的噪声都是互相独立的。

① 先验状态估计：

(17)

② 先验估计误差协方差：

Pk/k-1=AkPk-1AT+Q

(18)

③ 卡尔曼增益：

Kk=Pk|k-1HT(HPk|k-1HT+R)

(19)

④ 后验状态估计：

(20)

⑤ 后验误差协方差：

Pk=(I-KkH)Pk|k-1

(21)

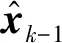
3.3 陀螺仪与加速度计输出值转换

由于陀螺仪输出的是电压值而系统需要的是陀螺仪检测到的角速度，因此需要对陀螺仪测得的电压值进行转换。其输出的电压值与对应加速度值的转换关系为

(22)

式中，G为陀螺仪检测的角速度；Vout为陀螺仪输出电压；Voffest为陀螺仪静止时的输出电压；Vsen为陀螺仪灵敏度；K为放大电路放大系数。

同样加速计参数的转换公式为

(23)

式中，A为加速度计检测的加速度；Vout为加速度计输出电压；Voffest为加速度计在平衡位置的输出电压；Vsen为加速度计灵敏度。

得出上述结果之后可以通过反三角函数得出与重力方向之间的夹角，但是此时得出夹角的单位为弧度，可以通过式(24)进行换算得出角度。

(24)

3.4 调试结果

调试过程首先需要对滤波器的各个参数进行设定。本系统中需要设定的值主要有三个：① Q_gyro为陀螺仪权值；② Q_angle为加速度计的权值；③ R_angle为卡尔曼增益。

前面已经完成了对示波器参数的设置，开始向上位机传输数据。此时平衡机器人处于平衡位置，通过施加外力使其与平衡位置产生一定夹角，通过上位软件的波形显示可以看到输出波形如图9所示，标号“1”表示加速度计测量的倾角曲线；标号“2”表示经卡尔曼滤波后产生的波形。从图9中可以看出将两者的数据融合滤波后得到的波形变得十分平滑，并在波形变化过程中无毛刺出现，并能够精确显示出平衡车的姿态信息。

图9 卡尔曼滤波器输出波形

通过观察放大后的波形如图10所示,可以看出倾角改变会导致滤波器产生一定的滞后，这种滞后情况的存在会影响控制系统对姿态调整过程。这不利于机器人的稳定性，因此需要修正滤波的参数，然后观测修整后输出波形的效果。

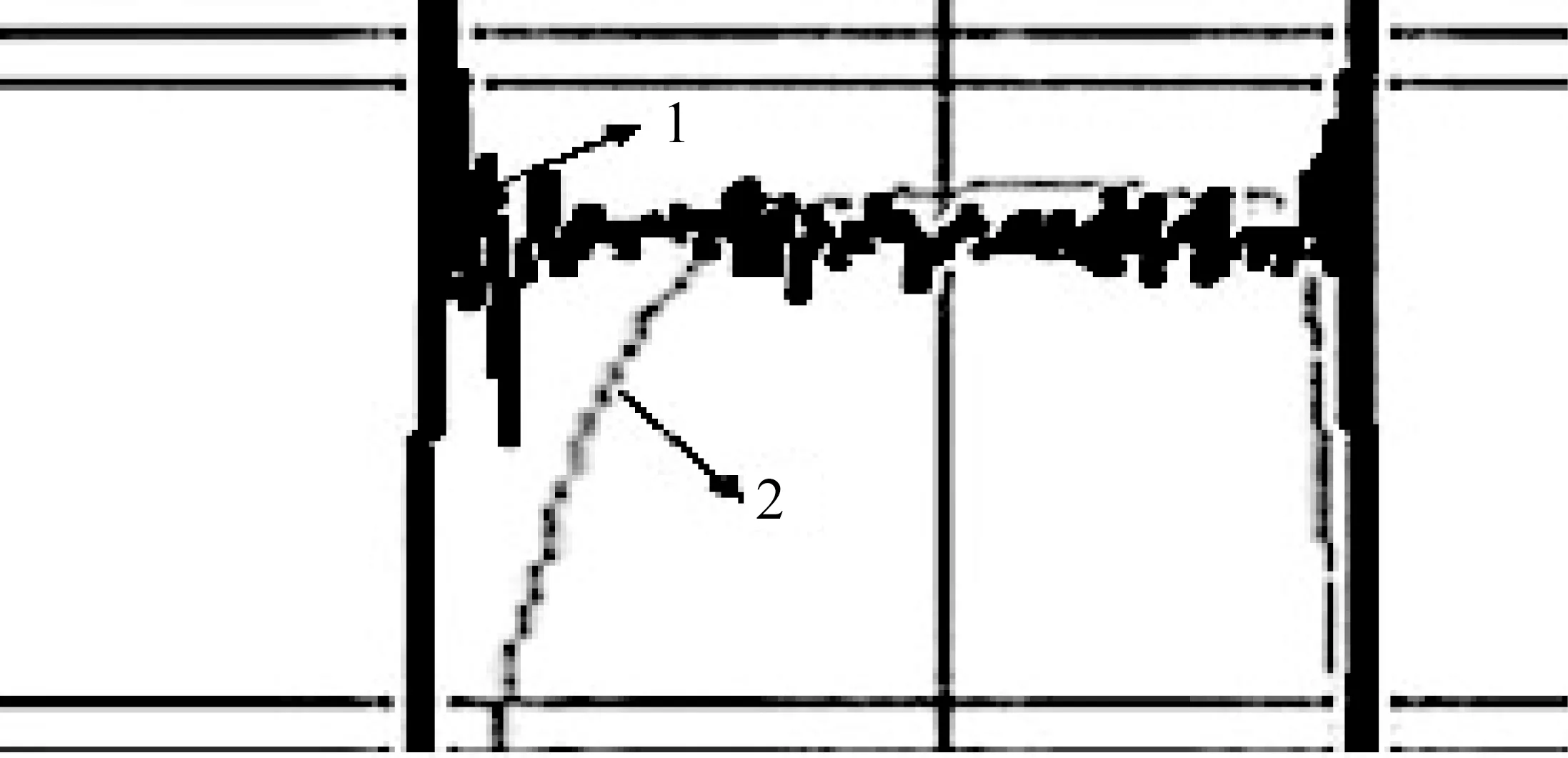
图10 放大后的波形

经过参数调整后，输出波形的滞后情况与未调整之前相比有了明显的改善，波形表面的毛刺大幅减少，波形曲线也更为光滑，如图11所示。

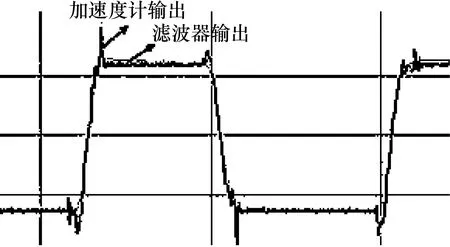
图11 参数调整后输出波形较

4 结束语

针对两轮自平衡机器人运动过程中可能出现的状态进行建模分析，并根据其运动方程设计两轮机器人的控制过程。在姿态检测过程中分析了两轮平衡机器人姿态检测过程中直接使用陀螺仪和加速计输出的数据对检测产生的影响。针对两者产生信号的特性采用卡尔曼互补滤波能够有效消除输出信号的毛刺，减少输出姿态角的动态误差，提高了检测精度，能够满足两轮机器人的姿态控制需要。对数据的处理方式同样适用于医疗健康设备中对人体姿态检测等相似的系统。