局部锈蚀钢箱梁腹板抗剪承载力数值模拟研究

林 春，张利忠

(浙江交工集团股份有限公司，杭州 310051)

0 引 言

沿海地区的钢结构桥梁在服役期间，由于长期处于海洋与工业大气下的复合侵蚀作用，其结构材料性能会逐步降低，甚至出现构件因锈蚀形成累积损伤而失效的现象，从而影响了结构的安全性。对于使用多年的钢箱梁桥，箱梁的锈蚀一般发生在支座处，支座位置的锈蚀使得钢箱梁腹板的厚度减薄，从而影响钢梁腹板的抗剪强度和剪切破坏模式[1]。钢箱梁腹板在剪力作用下的典型破坏模式为主压应力方向的屈曲破坏[1-2]。在钢梁腹板屈曲前，腹板在剪力作用下，其主拉应力与主压应力大小相等，如图1(a)所示；随着剪力增大，达到或超过腹板的屈曲强度时，腹板将不再承受更大的压力，增加的剪力主要依靠增大的拉应力承担，如图1(b)所示；腹板的抗剪极限承载力主要取决于图1(c)所示的拉力场及塑性区(图1(c)中的Cc)。各国文献资料中对钢板梁抗剪极限承载力给出了不同的设计公式，但主要区别为拉力场角度、翼缘对腹板约束条件及横向加劲肋的约束条件等[3]。

影响钢材及钢构件锈蚀问题的因素众多，如温度、相对湿度、空气中氯离子含量及湿润时间等，因此，钢构件腐蚀的形式和形状比较复杂[4-6]。钢梁腹板的锈蚀一般可以分为均匀锈蚀、局部锈蚀和点锈蚀三种类型。对均匀锈蚀，计算钢梁抗剪极限承载力可直接对腹板厚度进行折减[7-9]；而局部锈蚀和点锈蚀的锈蚀(蚀坑)深度、数量、位置、形状具有较大随机性，局部锈蚀或点锈蚀会造成钢板局部减薄或缺失，这会严重降低钢梁的承载力[9]，因此，有必要对局部锈蚀钢梁腹板剩余抗剪承载力及剪切失效模式进行评估。而目前，对于钢梁腹板局部锈蚀后的剩余抗剪承载力还缺少有效的标准和计算方法，另外，关于钢梁腹板局部锈蚀后的剪切破坏模式缺乏足够的分析。

以局部锈蚀的Q345qC钢箱梁为对象，通过数值分析，变换钢梁腹板锈蚀体积损伤程度及几何参数，对局部锈蚀影响下钢箱梁抗剪强度的变化趋势进行研究，并通过数据拟合，获得点蚀影响下钢箱梁的抗剪极限承载力计算公式。

(a) 屈曲前

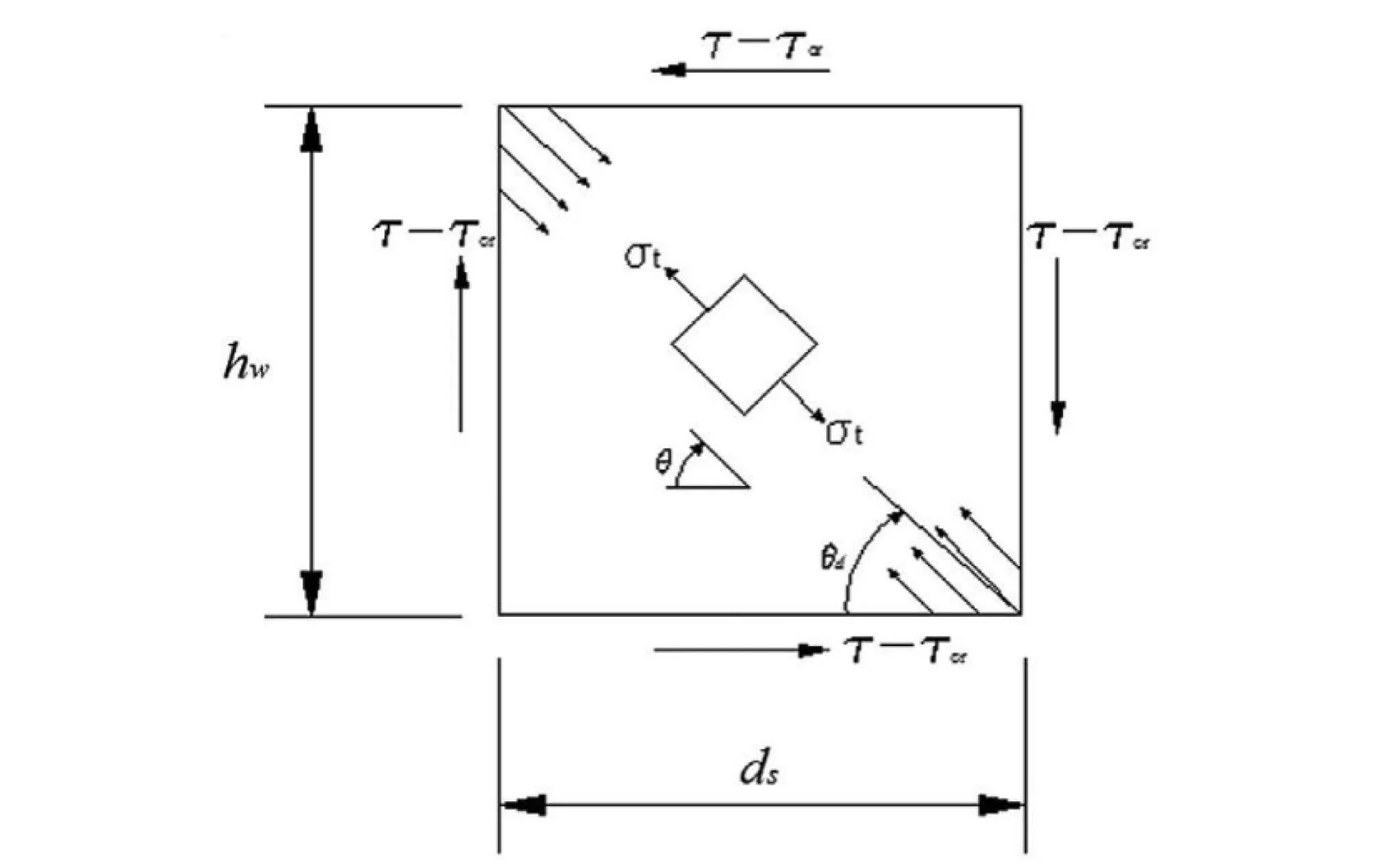
(b) 屈曲后

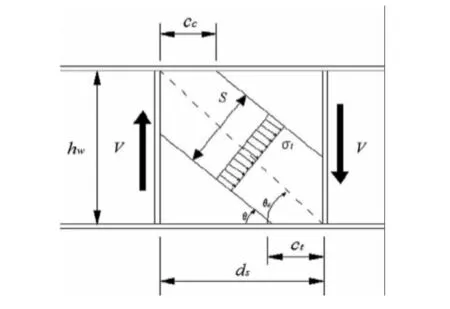
(c) 腹板拉力场及倾角

1 有限元模型验证

采用ANSYS软件进行建模，腹板、翼缘、加劲板均采用壳单元(SHELL181单元)进行模拟，局部锈蚀损失采用壳单元的偏移功能实现。为验证有限元分析模型的有效性，先按照文献[10]的试件尺寸建立了模型，后将有限元分析得到的钢箱腹板剪切强度变化规律和剪切破坏模式与文献[10]的试验结果进行对比。

1.1 有限元分析工况

文献[10]的试验为机械加工减薄模拟局部锈蚀作用的钢箱梁剪切性能试验，该试验共有6根钢梁，分别是5根腹板局部锈蚀的钢箱梁试件和1根腹板未削弱的钢箱梁对照试件。试件尺寸及示意图如图2所示，钢箱梁编号及锈蚀参数见表1。钢箱梁腹板高度及厚度分别为600mm和6mm，钢箱梁翼缘宽度及厚度分别为408mm和6mm。钢箱梁整体采用Q345qC钢材加工，单向拉伸材性试验得到钢材的屈服强度和极限强度分别为358.73MPa和500MPa。在钢箱梁试件跨中进行静力加载。

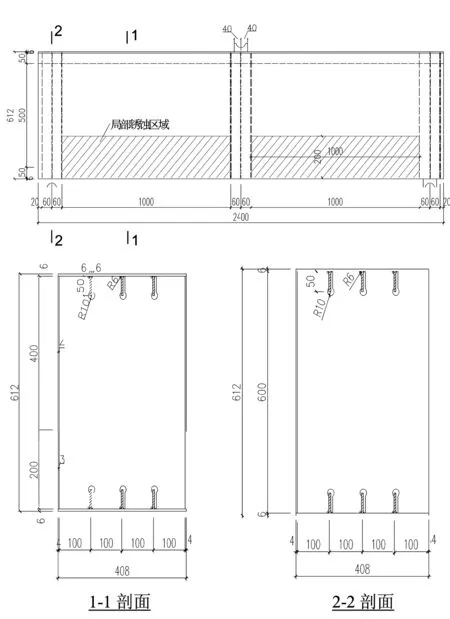
1-1剖面 2-2剖面

(b)试件示意图

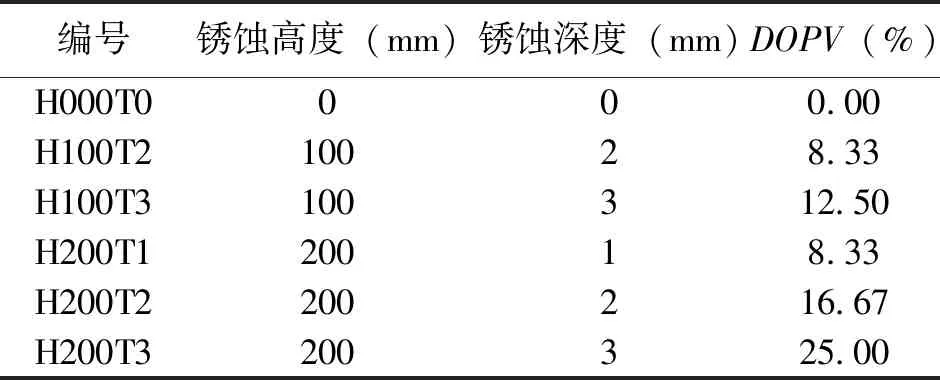
编号锈蚀高度(mm)锈蚀深度(mm)DOPV(%)H000T0000.00H100T210028.33H100T3100312.50H200T120018.33H200T2200216.67H200T3200325.00

注：H表示锈蚀区域高度，T表示锈蚀深度，DOPV表示锈蚀体积损伤程度[10]。

钢板材料采用三折线模型，材料曲线与实际材料特性尽量一致。其中，拉伸屈服强度取值为358.73MPa，抗拉强度取值为500MPa。钢箱梁有限元模型几何尺寸与试验试件保持一致，模型两端支座采用铰支座，约束其中一个支座的平面外位移、平面内水平位移及竖向位移，约束另一个支座的平面外位移、平面内竖向位移，荷载均匀施加在跨中节点处。

1.2 模型验证

关于局部锈蚀钢箱梁腹板抗剪极限承载力，试验值和有限元值的比较如表2所示，各组试件有限元值与试验值吻合度较好，平均误差在8%左右，导致误差的主要因素为试件加工焊缝及残余应力的作用没有在有限元模型中考虑。图3为各试件数值计算与试验破坏形态对照图，可以看出，各试件的有限元计算得到的破坏形态与试验破坏形态较为一致，破坏模式均为钢箱梁腹板面外屈曲破坏。由此可证明，采用通用有限元软件ANSYS可较准确地模拟局部锈蚀钢箱梁的抗剪性能。

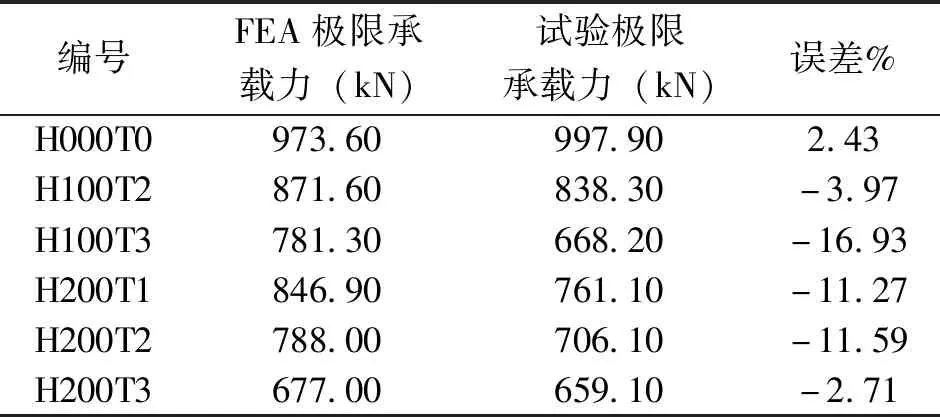
表2 试验及有限元抗剪极限承载力对比

(a) H000T0

(b) H100T2

(c) H100T3

(d) H200T1

(e) H200T2

(f) H200T3

2 钢箱梁腹板抗剪极限承载力的计算

2.1 不同锈蚀体积损伤程度的钢箱梁腹板抗剪极限承载力

建立了如图2所示钢箱梁的有限元模型，研究锈蚀体积损伤程度(DOPV)对局部锈蚀下腹板抗剪承载力的影响规律。计算结果列于表3及图 4，可知，同一钢箱梁腹板抗剪极限承载力的退化与DOPV表现出了极大的相关性，既DOPV越大，承载力下降越多。

表3 极限承载力随DOPV的变化

2.2 不同几何尺寸的钢箱梁腹板抗剪极限承载力

腹板的抗剪极限承载力主要取决于张力场及塑性区，不同几何尺寸将导致腹板产生不同的鼓曲波形和波形偏转程度，进而影响钢箱梁腹板的抗剪极限承载力。设计共11组不同腹板高厚比、宽高比以及翼缘厚度的钢箱梁模型，每组钢箱梁模型又包含了多个DOPV工况，共对多达60多个模型进行了计算，模型参数如表4所示。

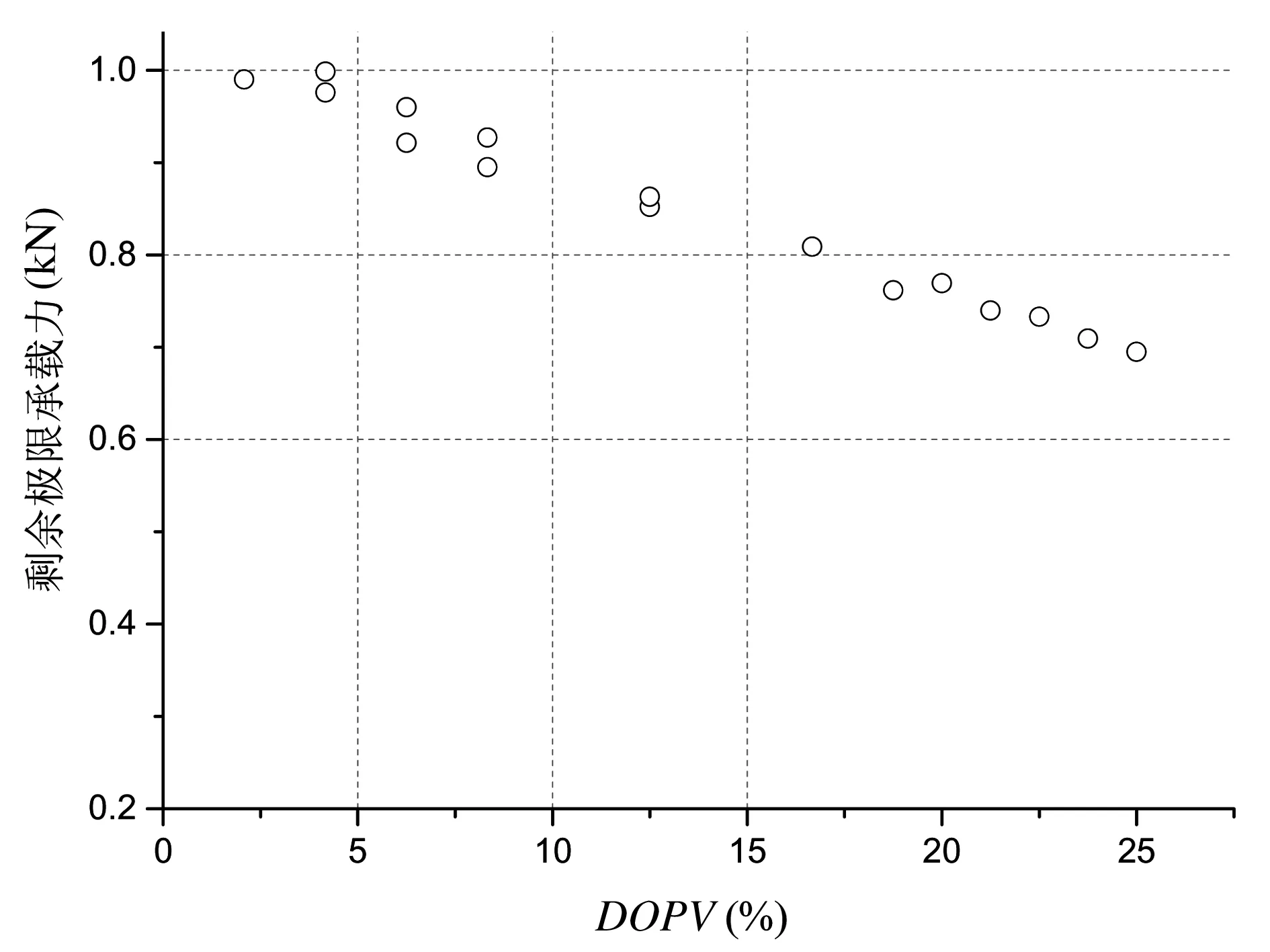
图4 极限承载力随DOPV的变化

编号腹板宽L腹板高hW腹板厚tW翼缘厚度tf1100060046210006003638008004641000100066510008006661000800467100080041281000800369100040046101000600612111000120046

有限元计算所得结果如图 5所示，可知随锈蚀体积损伤程度DOPV的增大，钢箱梁剩余抗剪承载力呈下降趋势；而相同DOPV，不同腹板高厚比、宽高比与钢箱梁的剩余极限承载力的关系表现为较大的离散性，其难以根据散点拟合得到统一的剩余抗剪承载力计算公式。因此，DOPV不适宜作为参数来反映局部锈蚀对钢箱梁极限承载力的影响。

图5 不同几何参数钢箱梁极限承载力随DOPV的变化

2.3 抗剪极限承载力公式拟合

由图 5可知，箱梁腹板剩余抗剪承载力与腹板高厚比、宽高比、DOPV等参数相关，但单一参数均难以衡量抗剪承载力的变化，所以必须提出能综合考虑各种影响的参数。为此，提出综合性影响参数γ，γ可以直观描述剩余抗剪承载力的变化见式(1)：

(1)

式中：β1为反应宽高比的影响系数，

h/t≥150时，β2=150/(h/t)，h/t<150时，β2=(h/t)/150 。

图6显示了局部锈蚀钢箱梁腹板剩余抗剪承载力随γ变化曲线。可以看出，γ能够综合反映锈蚀抗剪承载力的变化，γ值与钢箱梁剩余极限承载力呈现较好的线性关系，可以更为全面的描述不同高厚比、宽高比、锈蚀体积损伤程度对钢箱梁剩余抗剪承载力的影响。对图中所得数据点进行包下限拟合，拟合直线如图6所示。

拟合公式表示为式(2)：

(2)

式中：Vcu为钢箱梁在局部锈蚀作用下的剩余抗剪承载力；Vu为钢箱梁未受局部锈蚀影响的抗剪承载力。

由图6可知，公式值与有限元值相比，较为保守，有充裕的安全储备。

图6 极限承载力随γ的变化

3 结 语

(1) 随锈蚀体积损伤程度DOPV增大，钢箱梁剩余抗剪承载力呈现下降趋势；对于相同锈蚀体积损伤程度DOPV，不同腹板高厚比、宽高比与剩余抗剪承载力的关系离散性较大。

(2)拟合了局部锈蚀钢箱梁腹板剩余抗剪承载力计算公式；公式值较为保守，有充裕的安全余量。

(3) γ较DOPV，在考虑不同高厚比、宽高比、点蚀程度对钢箱梁剩余抗剪承载力的影响方面更为全面。