有关函数图像识别问题的探究——由2019年全国卷Ⅰ理科第5题引发的思考

杨跃山

（福建省漳浦第二中学，福建 漳浦 363200）

一、问题提出

函数图像的识别问题是高考中常见的题型,近三年全国卷均出现这种题型。为何命题老师喜欢以这样的题型来考查学生呢？因为这样的题型以简单的解析式呈现却能考查学生对函数三要素（定义域、对应关系、值域）、函数与导数图像的关系以及函数性质（单调性、奇偶性、周期性、对称性、最值、极值）等问题掌握情况。在解答此类型题的过程中又涉及到两大数学思想（数形结合思想、化归转化思想）。这样的题型有这么重要的作用那么它是否有通用而又简单的方法能以最快的速度找出正确的答案呢？下面对近三年全国卷的函数图像识别题目进行探究。

二、真题呈现

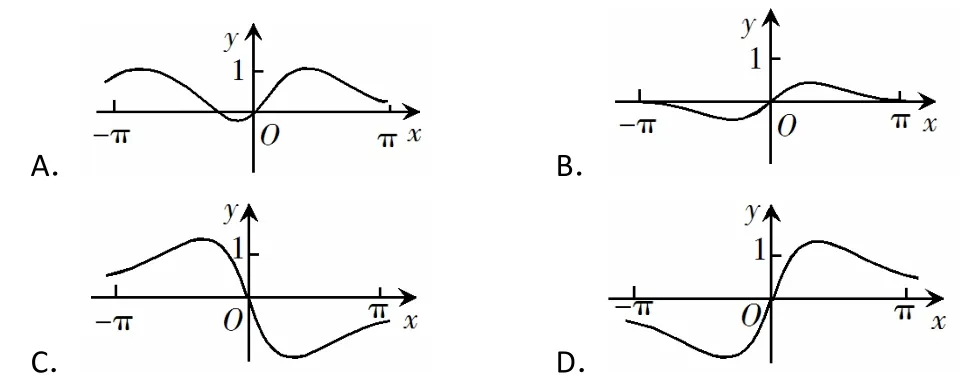
解析：先观察四个选项图像的特点，其中 B,C,D三个选项图像都关于原点对称。因此，我们先从函数的奇偶性入手，由确定该函数为奇函数其图像关于原点对称，故排除A选项。继续观察B,C,D三个选项的不同点，发现f(π)的值都不一样

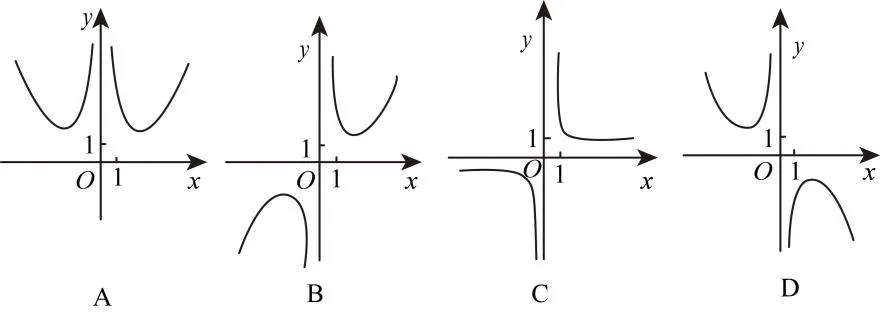
解析：通过研究函数奇偶性以及单调性，确定函数图像.

法一：特殊值法：由 f(3 )＞f (2) ＞0确定选项B

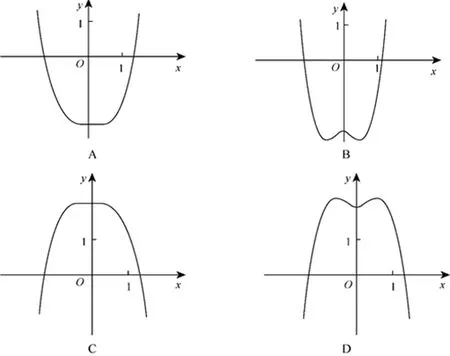
解析：法一：特殊值法：由 f (0)=2排除A和B 选项，由排除C 选项，

故选择D

三、解题思路归纳

由以上四道高考真题我们不难发现：已知函数的解析式确定函数的图象，往往从以下几方面考虑：①定义域： 确定图象是否连续，在哪个区域出现间断；②奇偶性：确定图象的对称性其中奇函数图像关于原点对称，偶函数图像关于y轴对称;③单调性： 确定图象的上升与下降趋势。判断函数的单调性可以通过导数求单调区间或者利用基本初等函数的单调性来确定。④ 最值：确定图象的最高点或最低点。常用求最值方法有导数法、配方法、基本不等式法等等。⑤周期性：常用于三角函数和抽象函数。求周期的常用方法有：定义法、公式法、图像法、转化法。⑥特殊点的函数值：通过特殊函数值排除不符合该函数值的选项。

其中求特殊点的函数值最为好用，但使用特殊值法需要注意以下几点：

第一：要在函数的定义域内取一些特殊值，取完后的特殊值才能满足要求；

第二：取特殊值要根据选项中给出的图像选择恰当的点（函数值不同）；

第三：取特殊值一定要让计算变得简单或者能够直接得出答案；

四、总结

高考对函数图像与性质的考查主要通过给出函数解析式识别函数图像

（一）考查函数类别

二次函数、三次函数、指数函数、对数函数、三角函数以及一些基本初等函数结合，这需要我们平时对高中所学的这些函数图像要熟练掌握，并能灵活运用。

（二）考查函数的性质

函数的定义域、值域、最值、奇偶性、单调性、周期性、对称性、零点等。这需要我们平时要积累求以上性质的常用方法。

（三）数学思想方法

特殊值法、排除法、数形结合方法、转化与化归方法。

因此，解决该类型题我们需要结合图像选择恰当的方法求出函数性质才能以最快的速度选出正确的答案。