船体应力释放孔的设计

谢小龙1，罗仁杰1，次洪恩1，许金波，张鹏

(1.中国船舶及海洋工程设计研究院，上海 200011；2.江苏新扬子江造船有限公司，江苏 泰州 214532)

在设计过程中，由于各种原因，船体构件几何形状会发生突变，例如，散货船横舱壁底凳的上下折角点，油船底边舱内底处的折角点。在发生结构几何突变处，由于应力集中现象的存在，结构构件的局部应力水平特别高，在设计和建造过程中需要重点关注。为了降低这些高应力区域的应力水平，传统的做法是增加板厚[1]或者新增一些局部构件[2]，或者是改变结构型式[3-4],在原设计的基础上做加法。这些做法会导致结构重量增加，使得建造工艺更为复杂。如果在局部高应力区域适当地设置开孔(定义为应力释放孔)，通过做减法的方式也可以有效降低船体结构的局部高应力水平。相对于传统的结构加强方法，在高应力区域设置应力释放孔，可以有效节省船体建造成本，提升船厂经济效益。在船体结构设计领域，关于应力释放孔的设计原则和理论探讨鲜有公开发表的文献记录。因此，考虑通过分析应力释放孔的作用原理，采用数值方法考虑应力释放孔的形状、尺寸和位置等设计参数对应力改善效果的影响规律，得出船体结构应力释放孔的一般设计原则。

1 应力释放孔的作用原理

应力释放孔一般设置在由于应力集中引起的船体结构局部高应力区域，如结构折角点处。以某散货船槽形横舱壁的底凳上折角点为算例，对应力释放孔的作用原理和选择进行阐述。

1.1 作用原理

某散货船槽形横舱壁的典型纵剖面见图1。

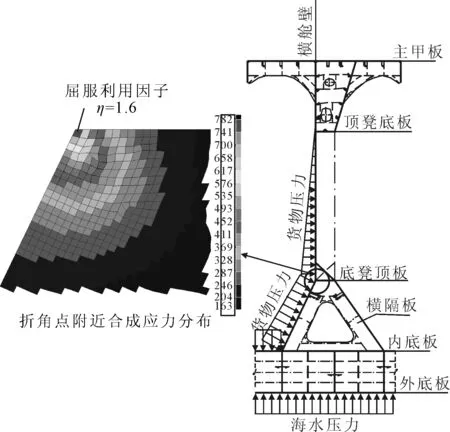
图1 某散货船槽形横舱壁纵剖面结构示意

根据舱段有限元分析结果，对于底凳上折角附近结构的构件尺寸，其决定工况为隔舱装载工况，即在重货舱一侧受到货物压力，船底及舷侧受到海水压力，同时整个横剖面承受一定的船体梁载荷。将槽形横舱壁结构简化为一定间距的单跨梁模型，上下端点处分别由顶凳和底凳提供近似刚性支撑。根据梁理论，最高应力出现在单跨梁的下端点，也就是底凳顶板支撑处。由于底凳顶板处(底凳上折角点)的结构形式复杂，几何形状不连续，且底凳不能视为槽形舱壁的完全刚性支撑点，梁理论无法给出该处结构的精确应力水平。采用三舱段有限元方法，并对底凳上折角点处的网格进行细化(该处结构净板厚25 mm,但为了准确模拟应力释放孔的几何形状，细化网格尺寸取为10 mm×10 mm)，求解该处的详细应力分布。计算结果显示，底凳横隔板在上折角点附近的应力集中现象十分突出，最大应力峰值出现在折角点处。

分析折角附近的主应力分布，见图2，发现折角点附近单元的第一主应力σ1远大于第二主应力σ2，并且越靠近折角点，这一现象越明显。

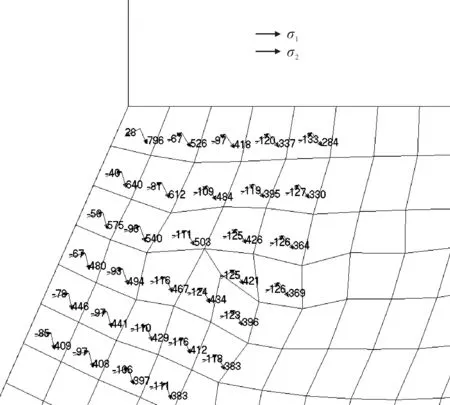
图2 底凳横隔板上折角点处主应力分布

根据材料力学强度理论[5]，由式(1)，在σ1远大于σ2的情况下，如果减小σ1，则能有效减小折角点附近的合成应力σe。再由式(2)，通过减小折角点附近单元的应变ε(变形量)，则可以减小主应力σ1，进而减小合成应力σe，从而达到降低高应力区域应力水平的目的。

(1)

(2)

式中：E为材料弹性模量；u为单元在主应力σ1在x方向上的位移。

根据此原理，通过在折角点附近适当地设置开孔(应力释放孔)，结构材料在开孔边缘得以自由变形，可以有效减小局部结构在外载荷作用下的变形量，降低高应力区域结构的应力水平。

1.2 应力释放孔的选择

并非任意形状和位置的开孔都可以作为应力释放孔，如果开孔的设计不合理，往往适得其反。对于50 mm×50 mm细化网格，邻近焊缝单元的许用应力相对标准网格放大1.5倍，非邻近焊缝单元的许用应力放大1.7倍，即非邻近焊缝单元的许用应力衡准与邻近焊缝单元不同，相比之下非邻近焊缝单元许用应力高出13%。因此，需对不同位置单元的屈服利用因子按式(3)～式(5)进行归一化处理，方能客观评价设计方案的安全性。屈服利用因子η越小，则表明设计方案的安全性越高。

η=max(η1,η2)

(3)

(4)

(5)

式中：[σe]为标准网格的许用应力,算例采用AH36高强度钢，[σe]=326 MPa；η为设计方案的屈服利用因子；η1、η2为邻近焊缝和非邻近焊缝单元的屈服利用因子。

采用10 mm×10 mm细化网格，实船评估时可根据文献[5]的要求，将单元应力按面积加权平均到50 mm×50 mm的区域再进行评估。为了更直观地比较不同设计方案的应力峰值水平，仍采用50 mm×50 mm细化网格许用衡准，对不同位置单元利用因子进行归一化。

图3为船体结构设计中常用的开孔形式，以及开孔后折角点附近单元在决定工况下的应力分布和最大屈服利用因子。

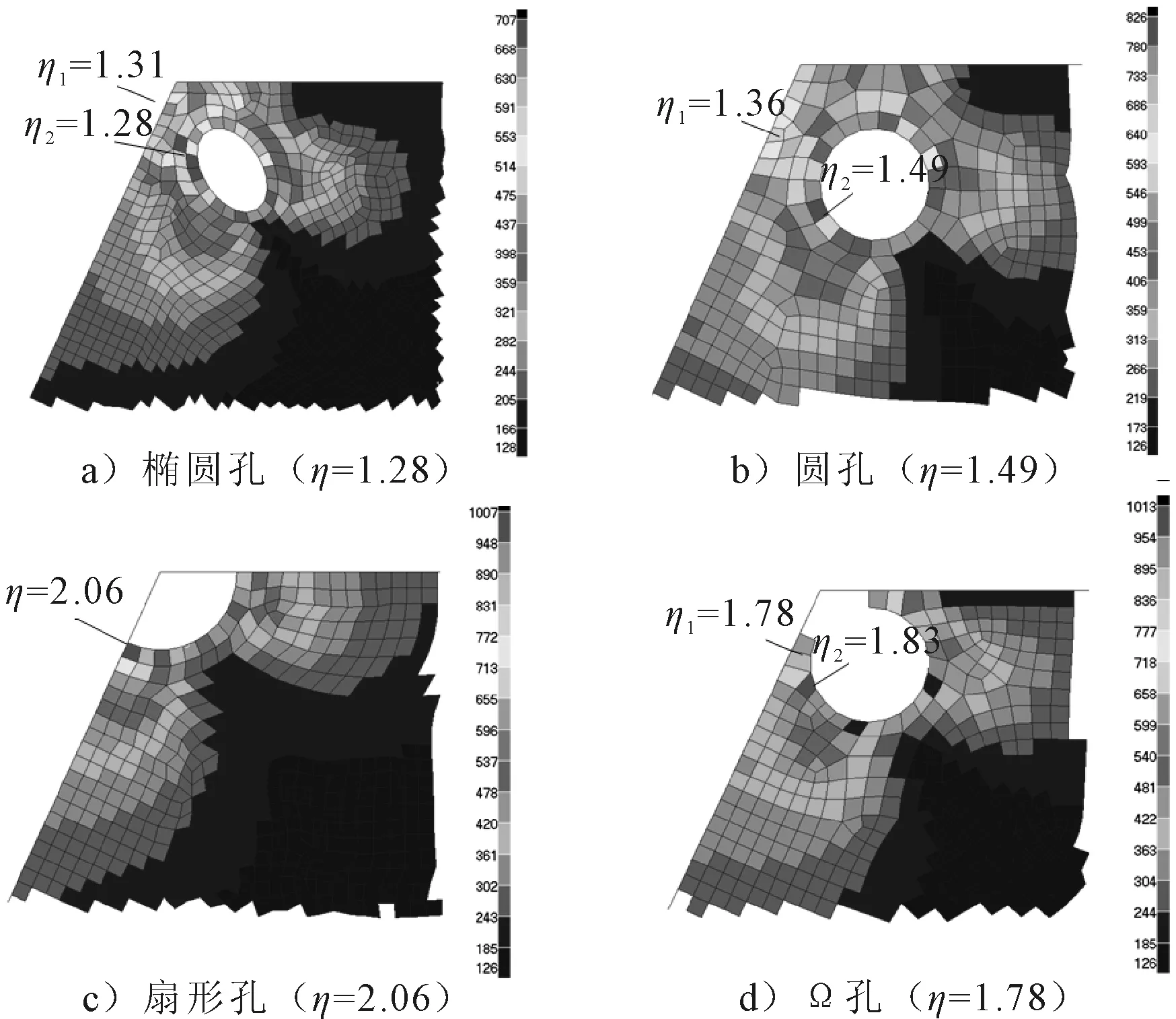
图3 常用开孔形式及决定工况下应力分布

对比图1中开孔前折角点附近的应力分布和最大屈服利用因子，可以得出以下结论。

1)椭圆孔和圆孔可以大幅降低紧邻折角点处单元的应力水平，但应力峰值转移至开孔边缘处；椭圆孔自由边处的应力峰值较开孔前进一步减小，屈服利用因子大幅降低(η由1.6降至1.31)；圆孔自由边处应力峰值较开孔前有所增加，但开孔边缘非邻近焊缝，许用应力衡准也相应提高，综合下来屈服利用因子仍有所降低(η由1.6降至1.49)。

2)扇形孔和Ω孔反而会增加紧邻折角点处材料的应力水平，对结构安全不利，不适合作为应力释放孔；结构共同规范不允许在该折角点处设置切口的要求合理。

比较其他工况下的应力水平，发现椭圆孔和圆孔对折角点附近的应力水平有相近程度的改善。椭圆孔和圆孔均可以作为应力释放孔，可降低折角点附近结构的屈服利用因子，提升结构安全性；椭圆孔的应力改善效果更优。

2 设计参数

应力释放孔对高应力区域应力改善效果的影响主要取决于其形状、尺寸和位置。与圆孔相比，椭圆形应力释放孔的应力改善效果更优。以椭圆孔为例，着重讨论尺寸和位置参数对应力改善效果的影响。椭圆应力释放孔的尺寸设计参数包括短轴a和长轴b，位置设计参数包括开孔距高应力区域中心点的距离d和转角θ。见图4。

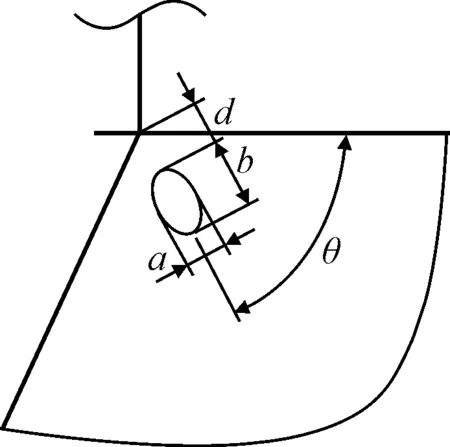
图4 应力释放孔的主要设计参数

采用参数化建模技术，快速自动生成不同参数组合下的有限元模型，分别考虑这些设计参数对应力改善效果的影响。

2.1 开孔尺寸

为了考虑不同尺寸椭圆孔对应力改善效果的影响，将开孔位置参数d和θ设为恒定值，椭圆短轴a的取值范围为30～70 mm，计算间隔为10，共分为5组模型，每组模型长轴b的取值为短轴a的2倍左右，计算结果见表1。

随着a的增加，屈服利用因子η呈先减小后增大的规律，在a为50 mm时，材料的屈服利用因子最低，应力改善效果最好；当a数值一定时，b取略小于2a(最大不超过2a)，应力改善效果最好。

2.2 开孔距离

将开孔转角θ设为恒定值，分别考虑在开孔尺寸40 mm×70 mm，50 mm×90 mm和60 mm×105 mm情况下，开孔距离d对应力改善效果的影响，计算结果见图5。

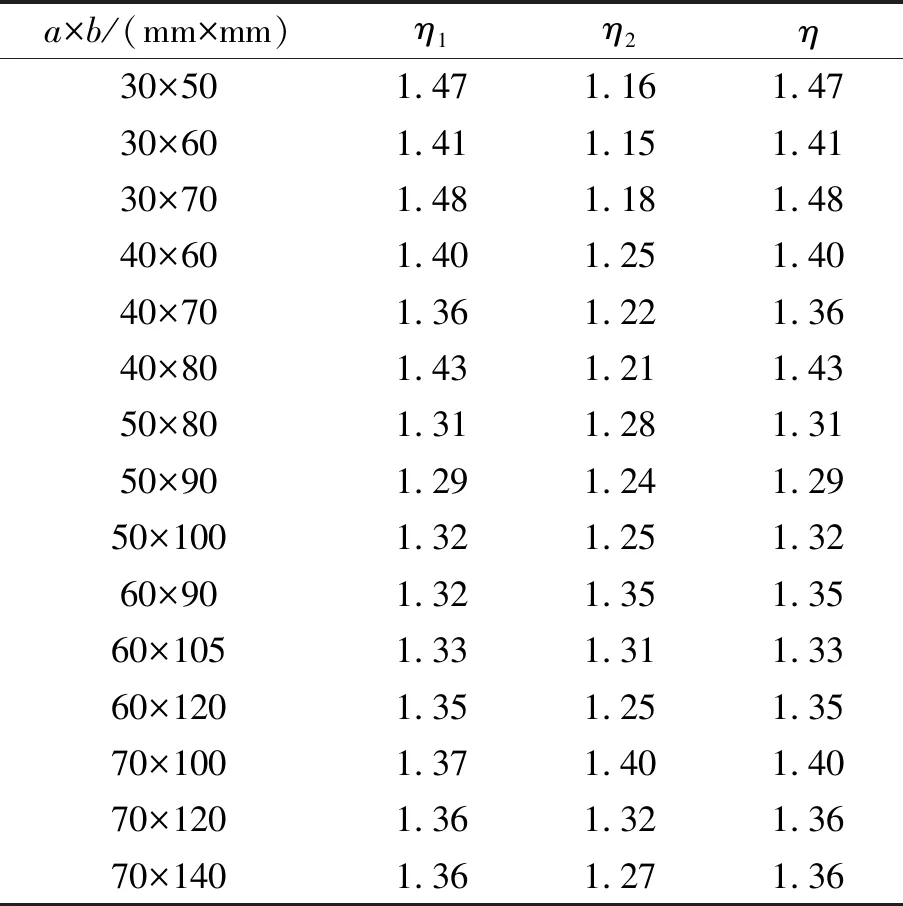
表1 不同开孔尺寸下折角点附近的屈服利用因子(d=50 mm，θ=57.5°)

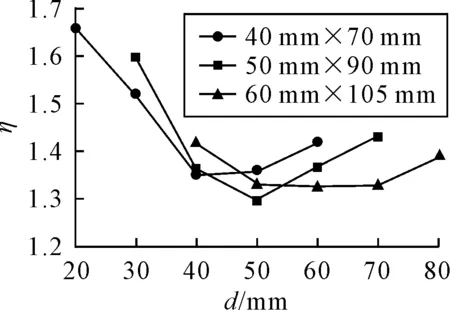
图5 折角点附近屈服利用因子与 开孔距离d的关系(θ=57.5°)

对每一开孔尺寸，随着d的增加，屈服利用因子呈先减小后增大的趋势；对于40 mm×70 mm椭圆孔，最佳应力改善效果出现在d=40 mm;对于50 mm×90 mm椭圆孔，最佳应力改善效果出现在d=50 mm;对于60 mm×105 mm椭圆孔，最佳应力改善效果出现在d=60 mm。因此，可以推断：开孔距高应力区域中心点的最优距离为d=a。

2.3 开孔转角

考虑在图5中3种开孔尺寸情况下，应力释放孔转角θ对应力改善效果的影响，对每一组开孔模型，取开孔距离d=a，计算结果见图6。

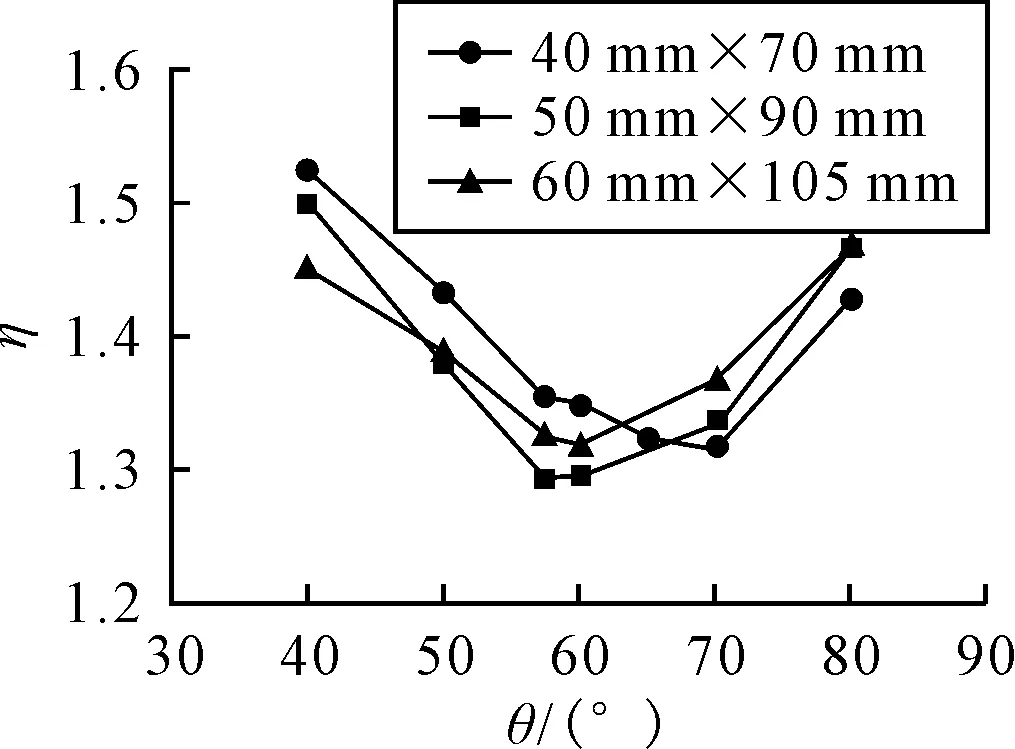
图6 折角点附近屈服利用因子与开孔转角θ的关系(d=a)

对每一开孔尺寸，随着应力释放孔转角θ的增加，屈服利用因子呈先减小后增大的趋势；对于50 mm×90 mm和60 mm×105 mm椭圆孔，最佳应力改善出现在θ=60°，对于40 mm×70 mm椭圆孔，最佳应力改善效果出现在θ=70°，考虑到折角点附近单元第一主应力σ1的方向也在60°左右(见图2)，结合1.1中关于应力释放孔的作用原理分析，可以推断应力释放孔的最佳转角θ应设置在高应力区域第一主应力σ1的方向上。

3 结论

1)通过合理设置应力释放孔，可以改善应力集中构件的高应力水平；椭圆孔和圆孔适合作为应力释放孔，但椭圆孔对高应力区域的应力改善效果更优。

2)对于椭圆应力释放孔，随着短轴尺寸的增加，其应力改善效果呈先增加后减小的规律；一般在短轴取为50 mm左右时，椭圆孔对应力改善的效果最优，长轴尺寸宜略小于短轴的2倍。

3)随着应力释放孔距高应力区域中心点距离的增加，其应力改善效果呈先增加后减小的趋势。对于椭圆孔，在开孔距高应力中心点的距离等于其短轴长度时，应力改善效果最佳。

4)应力释放孔的最佳转角应设置在高应力区域第一主应力的方向上，偏离主应力方向后的应力改善效果变差。