下肢康复机器人的运动控制设计*
2019-09-11徐中华穆载乐陈隆飞
徐中华, 方 娟, 穆载乐, 陈隆飞
(1.江南大学 机械工程学院,江苏 无锡 214122;2.江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
0 引 言
如果脑卒中患者能及时并合理地进行早期步态康复训练可以在一定程度上恢复步态行走的能力[1,2]。所以医学上通常对患者进行重复的、特定任务的训练活动,从而使重组状态下的大脑皮质经过不断地重复特定动作来进行再学习[3]。
相比传统的治疗方法,使用机器人辅助康复训练不仅能够减少治疗师的人员和体力消耗,而且能够更准确地进行康复训练,从而提高治疗效率,降低成本,节省康复医疗资源。
按功能目的康复机器人可分为辅助/替代型和训练/治疗型,按人机结合的方式分为外骨骼式和嵌合式,按移动方式又可分为移动式和固定式[4]。但是目前康复机器人在结构设计和控制方面的关键技术仍未取得较大的突破。本文针对课题设计的治疗型下肢康复机器人进行轨迹控制的研究。
1 下肢康复机器人的结构设计
本文的下肢康复机器人机械系统主要由下肢关节运动机构、减重支撑机构以及床体结构组成。下肢关节运动机构是康复机器人机械系统中的核心部分,主体功能是进行下肢髋关节、膝关节和踝关节的康复训练,机器人应具有较大的运动范围,以使患者在保证安全的前提下尽可能进行大幅度的康复训练。减重支撑机构用于减轻患者自身体重在下肢上的作用力,辅助患者进行康复训练,因承受载荷较大对机构的强度要求较高。床体结构用于连接减重支撑机构和下肢关节运动机构,并且可以给患者提供多种体位的训练模式,以提高对患者的训练效率。
在进行康复训练时,患者需要将身体贴合在机器人上,所以在进行康复机器人结构设计时应满足安全性、兼容性、舒适性、轻便性四个原则[5]。在安全性方面,在进行机械结构设计时选用较大的安全系数,避免出现角棱结构,同时使康复机器人的运动范围不超过人体生理学运动范围。在兼容性方面,按照大多数人的身高进行设计,同时根据人体各部分数据的经验公式算出人体各部分的长度范围,将其作为机器人的可调范围,本文机器人设计的适用对象是身高为1.5~1.9 m的患者[6]。在舒适性方面,应尽量使机器人中与患者贴合部分按照人机工程学进行设计。在轻便性方面,应在保证结构强度的基础上尽量选用材质轻的材料,机器人除了床体和减重机构中的加强筋选用钢,其他结构均选铝合金作为设计材料。根据以上几个原则,最终设计的下肢康复机器人如图1所示。

图1 下肢康复机器人机械结构总装
2 下肢康复机器人的运动控制设计
2.1 系统固有传递函数的确定
下肢康复机器人的关节旋转运动是通过电机带动滚珠丝杠推动相关肢体结构实现的。因各关节驱动装置的结构相似,本文以髋关节驱动装置为例进行研究。如图2(a) 为髋关节驱动装置的机械结构图,图2(b)为其结构简化图,由图知该结构可看作是一个变化的三角形。

图2 髋关节驱动机构
根据其传动结构,得到关节角度和电机驱动器输入信号的关系式
(1)
式中θ为髋关节角度,是图2(b)中∠DAG的角度值,取屈曲为正;θ0为大腿处于直立时∠BAC的角度值;k1为电机驱动器的速度增益;p为滚珠丝杠的导程;u1为电机驱动器的输入电压值;lAB为髋关节A点到大腿板与电机驱动装置铰接点B点的长度;lAC为髋关节A点到床体与电机驱动装置铰接点C点的长度;l0为滚珠丝杠装置处于最短长度时lAC在丝杠轴线方向上的投影长度。
由式(1)看出该髋关节驱动装置为非线性系统,不能进行直接利用线性系统的理论进行分析。针对非线性系统主要有控制方法:1)通过对模型进行简化近似,转变成线性系统进行控制;2)采用现代控制方法如变结构控制、模糊控制、神经网络控制等控制方法直接进行控制[7]。
本文采用前者进行控制设计,由于难以简化输入输出的关系式,为此可以利用实验的方法近似得到系统的传递函数,然后再进行线性控制。将髋关节驱动装置上与传感器、滤波器等接入电路,因机械装置运动受限,采用方波信号代替单位阶跃信号作为系统的输入,可以得到系统的输出响应。取不同周期的方波作为系统输入进行实验,均可得到类似如图3所示的结果。将输出结果与常见的响应曲线对比,发现其与积分环节的响应曲线相似,于是假定该系统的传递函数为
(2)
式中UO(s)为角度传感器输出值的像函数,U1(s)为电机驱动器输入值的像函数,k为髋关节驱动装置开环系统的增益。

图3 开环测试结果
对式(2)进行反拉氏变换,得到
duo(t)/dt=ku1(t)
(3)
式中uo(t)为t时刻下角度传感器的输出值,u1(t)为t时刻下电机驱动器输入值。从图3可以看出,在输入信号保持不变的半个周期内,输出值的斜率也不变,由此在半个周期内任取两点即可求得系统函数的增益
k=Δuo/(u1Δt)
(4)
式中 Δt为输入信号保持不变的半个周期内任取两点的时间差,u1为此时对应的输入值,Δuo为输出曲线上在该两点对应时刻的纵坐标值之差。
为防止偶然误差的出现,求出多组实验的k值,并从中筛选出3组取平均值,将其作为k值的最终结果,得到k=-1,系统的传递函数为
G0hip=-1/s
(5)
2.2 控制器的设计
为使下肢按照目标角度准确运动,同样对下肢各个关节驱动装置采用闭环控制。仍以髋关节为例进行设计控制器。
由于髋关节系统的固有传递函数为一阶系统,不妨采用极点配置的方法将系统配置成典型的二阶系统
(6)
式中ξ为阻尼比,ωn为无阻尼自振角频率。
设控制器
(7)
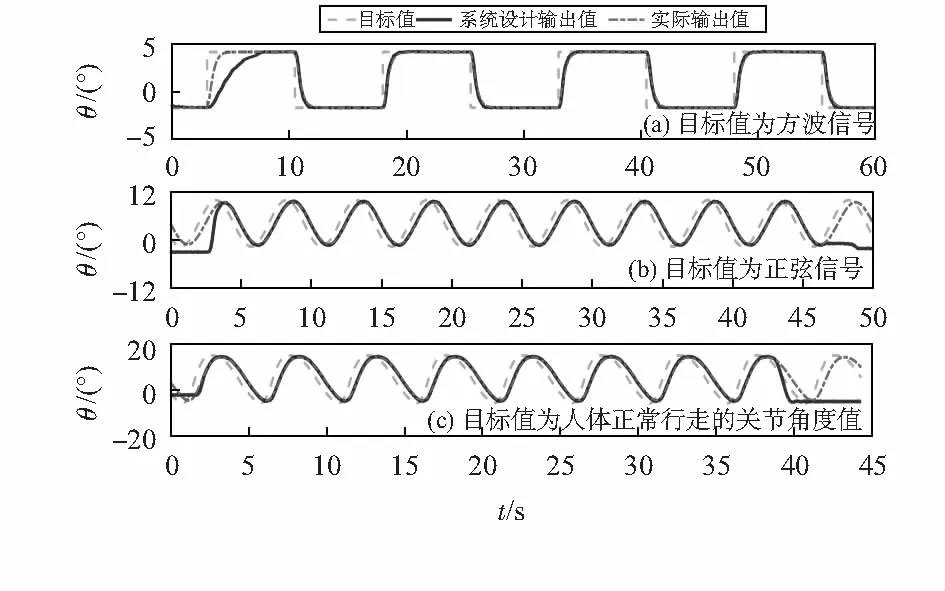
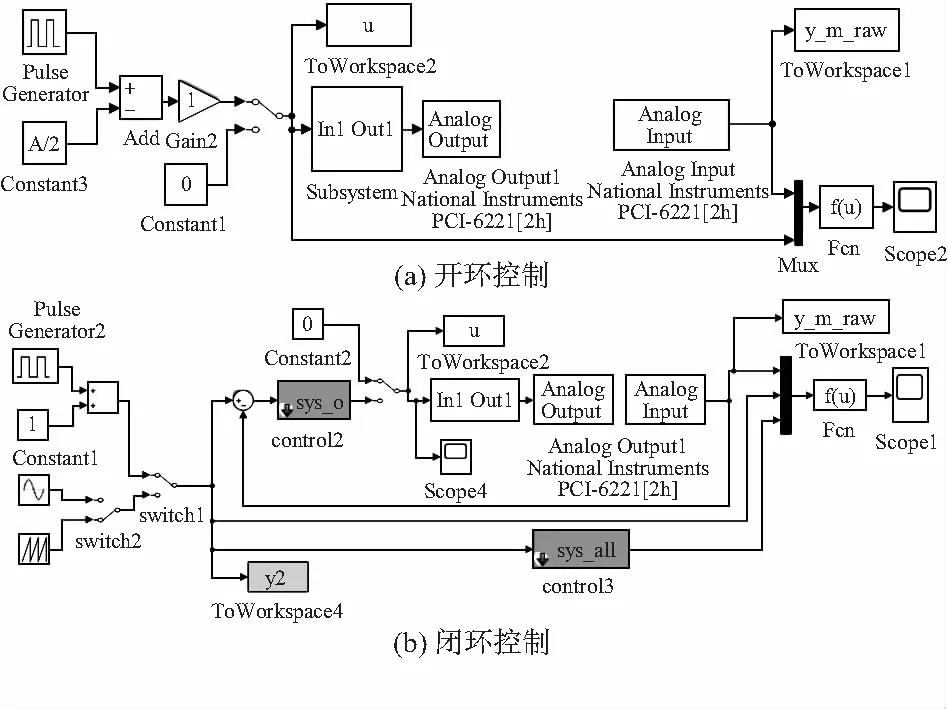
式中ng和nh为自然数,且有ng (8) 两项有理式要相等,首先要保证分子分母对应多项式的阶数要相等,可得 ng=0;nh=1 (9) (10) (11) 再由两项各项系数相等,可得 (12) 根据定义知,上升时间是指响应曲线从稳态值的10 %上升到稳态值的90 %所需的时间。当t>0时 xo(t)=1-(1+ωnt)e-ωnt (13) 令z=1+ωnt>1,则有 xo(t)=1-e(ze-z) (14) 令yo(z)=1-e(ze-z),并令f(z)=ze-z,则,f′(z)=(1-z)e-z,可知在z>1时f(z)为单调递减函数,yo(z)为单调递增函数,由此只需分别求出yo(z)=0.1和yo(z)=0.9在z>1的解,那么系统的上升时间tr即为两个解的横坐标之差的绝对值除以自振角频率ωn。由于难以直接求出方程的解,利用MATLAB绘出曲线的图形如图4,可以估算出上升时间 (17) 图4 上升时间求解 因此髋关节控制器的传递函数为 (18) 测试实验是基于MATLAB/SIMULINK平台上进行的,用户可以直接调用测试的采集模块,而且还提供了所需的实时环境,使得计算机与实物模型的数据能够同步传输。开环控制SIMULINK模型如图5所示。利用模型测得系统的开环传递函数,在图5的基础上加入了前面设计的控制器,建立了闭环控制SIMULINK模型如图5(b)所示。 图5 下肢康复机器人髋关节控制系统的模型 同时分别以方波信号、正弦信号、人体正常行走的关节角度值为输入,依次得到如图6的实验结果。从图6(a)看出系统无超调,计算得到髋关节控制系统的实际上升时间为0.85 s,与设计基本相符。从图6(b)看出控制器的跟踪效果较好,有稍微的延时。从图6(c)看出髋关节机构的运动情况与目标角度也非常接近,故所设计的控制器能够很好地满足实验要求。 因本文设计的下肢康复机器人各关节控制系统属于非线性系统,无法直接利用线性控制理论进行设计控制,为此通过实验的方法得到近似的传递函数,将其转化为线性系统的控制问题。同时采用了一种简单的极点配置方法实现了对控制器的设计。 图6 实验测试结果 下肢康复机器人髋关节控制系统采用上述设计的控制器进行运动控制,实验结果表明该控制系统在速度性和稳定性上都达到了很好的效果。因设计思想简单,可以将该配置方法推广到其他控制器的设计上。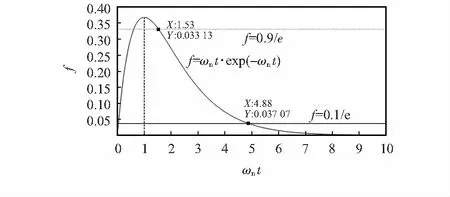
3 下肢康复机器人髋关节控制系统实验
4 结束语