行人紧急疏散仿真研究

王文玉，王希良，李为民

行人紧急疏散仿真研究

王文玉1，王希良1，李为民2

(1. 石家庄铁道大学 交通运输学院，河北 石家庄 050043；2. 石家庄铁道大学 土木工程学院，河北 石家庄 050043)

近几年来，紧急情况下人员安全疏散问题日益被重视。避免重大人员伤亡和经济损失，快速高效地将人员安全疏散，成为亟待解决的问题。以磁力模型为基础，考察独立步行个体的运动行为，将宏观角度上路径移动效益模型与微观角度上磁力模型、社会力模型有机结合起来，以接近现实中的行人移动行为。将个体行人运动上升为群体运动，提出元胞自动机的疏散模型，基于独立步行个体的运动行为添加约束条件，在Pathfinder软件中进行仿真模拟。仿真结果找出限制向出口移动的潜在瓶颈：交叉人流导致的瓶颈现象；疏散通道上不合适的转角造成的瓶颈现象；出口宽度的限制导致的瓶颈现象。并针对瓶颈现象，给出相应的措施。

磁力与社会力结合模型；Dijkstra算法；元胞自动机；Pathfinder仿真模拟

大量的国内外学者对紧急情况下的人员安全疏散问题进行了研究。姚刚等[1]基于P＆M经验公式建立以疏散时间最短为目标函数的数学模型，并通过Matlab仿真分析研究疏散人数、疏散间距以及地震烈度对疏散时间的影响。胡丽娟等[2]基于多智能体仿真平台NetLogo搭建仿真环境，利用智能体建立地铁车站站厅人员紧急疏散仿真模型。孙超等[3]联合使用火灾动态模拟软件和人员疏散模拟软件，开展火灾蔓延和发展规律以及人员紧急疏散情况的数值模拟研究。马建敏等[4]设计一种基于遗传算法的紧急疏散路径规划。李伟等[5]围绕影响轨道交通枢纽人员紧急疏散效果的疏散空间环境设计、疏散人员客流环境分析和疏散行为模式研究等3个关键领域，对国内外城市轨道交通枢纽紧急疏散技术相关现状进行了分析和讨论。SONG等[6]将社会力模型的力概念引入格子气体模型，构建一种新的基于LG的离散模型“多网格模型”，分析了相互作用力对疏散时间的影响。Pursals等[7]提出一个包含疏散路线的建筑物疏散问题的公式。Takimoto等[8]通过出口研究疏散过程中人群的逃逸时间分布。总体说来，研究紧急情况下的疏散问题包括两大方法，即数学建模和仿真模拟研究。现有研究方法没有将2种方法结合起来，单单的数学建模或者仿真模拟已不能满足紧急情况下快速高效地将人员安全疏散问题的需要。因此，本文从建模的宏观角度，将路径移动效益模型与微观角度上磁力模型、社会力模型有机结合，并进一步基于元胞自动机利用Pathfinder仿真，研究在紧急情况下快速高效地将人员安全疏散的问题。

1 行人移动模型

行人抽象有2种情况[9]，即圆形体抽象和椭圆体抽象。为了提高计算精度，接近实际情况，一般情况将行人看作椭圆体模型，但是椭圆体模型运算速度低，计算量大。本文主要研究宏观角度上路径移动效益模型，因此，为提髙运算速度，将行人抽象为圆形体。

该模型采用行人步行的期望速度。期望速度是根据环境影响情况、个人年龄状况等条件预先设置的期望值。参考文献[10]，行人期望步行速度符合均值1.34 m/s，标准差0.36 m/s的正态分布。

1.1 微观行人运动模型

磁力模型[9]的本质是同性相斥，异性相吸。磁铁的正极为行人和障碍物，负极为行走的目标点。在引力和斥力的双重作用下，行人向目的地运动，并避让其他的行人和障碍物。随着时间的改变，相应的周围状况都会影响行人的速度及位置[11]。磁力模型由作用力和加速度组成，作用力表示式如下：

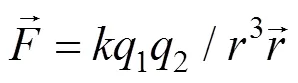
社会力模型是一种典型的微观连续模型，基于数学和物理解析方程而建立。社会力模型认为行人的运动主要受到驱动力、人与人的作用力和人与障碍物的排斥力，并非外力作用。磁力模型与社会力模型都建立了连续矢量空间。磁力模型有效避免行人过程中的碰撞，行为会与他人或障碍物保持一定距离，与社会力模型相比，磁力模型的行走路径相对固定，在行人与行人或障碍物的交互作用方面表现较弱。社会力模型描述行人运动较真实，能够反映行为与环境之间的交互作用。将微观角度上磁力模型、社会力模型有机结合起来，更加接近现实中的行人移动行为。

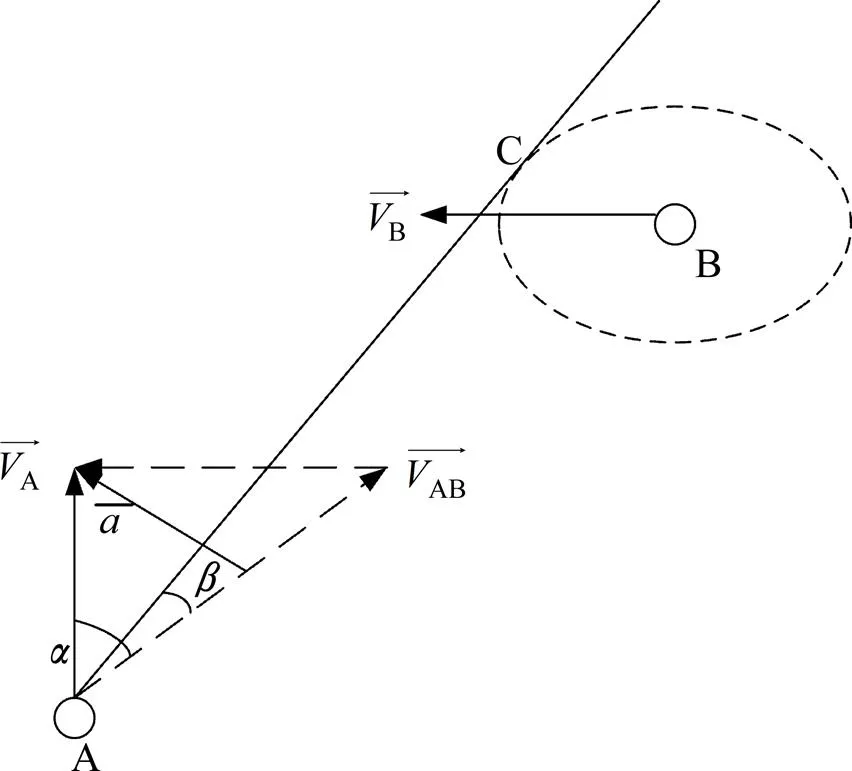
图1 磁力与社会力结合模型

1.2 宏观路径步行模型

在比较复杂的空间里路径有多种情况，简单模式下不能真实地表现群体移动状态。为更深层次地研究宏观运动的群体步行行为，本文利用磁力、社会力模型与移动效益模型相互结合，更加真实地再现紧急疏散情况下群体的移动。

移动效益模型用来表现行人在路径网络上的微观移动，在行人对路径的选择上非常重要。其方法是，假定被研究的空间内出现了拥挤的现象，路径成本不会以最短长度的路径来衡量，于是利用Dijkstra法求最优成本的路径就变得可行。这也意味着行人的步行轨迹是根据自己对周围环境和状况的判断，进行的合理的路径选择行为。具体步骤如下[12]：

1) 首先是建立建筑物仿真模型。观察并截取建筑物场景，从其中抽取典型设施和元素并简化为平面路径图。

2) 利用Dijkstra算法求最优成本的路径，给出路径选择的方法。

3) 利用磁力移动模型，适当变换行人移动 路径。

移动路径网络的路径成本计算需要考虑多种因素。当拥挤情况发生时，行人未必会按照最短的路径方向移动。因此，需要考虑多边形的重心间距离以及各个多边形内的行人密度。以上共同作用形成了路径成本。

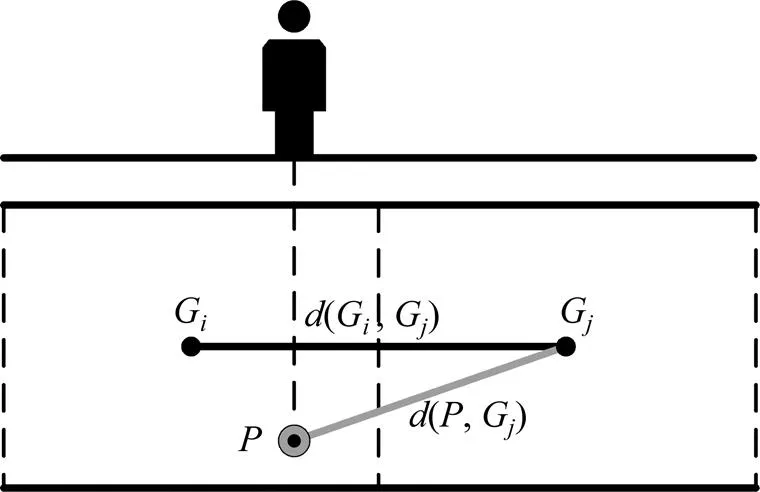
图2 路径距离长度

2 个体行为仿真研究

2.1 移动路径网络

本文研究卢浮宫平面图0层。首先将其平面图分解，原则上说，平面图中元素与周围不同须独立分割出来。但是对于卢浮宫来说，出口较多且布置有规律，大厅与大厅之间连接紧密，按照属性将部分结构各个环节分析出来不是必然，因此，将卢浮宫平面图分解为较有规则的部分。

假定行人将选择合理的路径，因此就能通过这种移动路径网络来表现宏观的个体行人移动行为。同时根据卢浮宫楼梯布置情况，假定出口。假定卢浮宫0层有14个出口，在此基础上有44个节点(注意：节点为线段，序号是所标注的每个点)。

2.2 拥挤时路径成本的计算

模型假设s=1.34 m/s，根据文献[13]可知，当人流密度为1.54 p/m2时，通道处的人流量达到最大值，楼梯处上行和下行人流量最大时对应的人流密度分别为2.14 p/m2和1.99 p/m2，由于模拟卢浮宫0层紧急疏散，不会出现游客上下逃离的情况，则按人流密度为1.54 p/m2来计算。根据公式，可得卢浮宫移动路径网络每个节点的拥挤时路径成本，如表1所示。

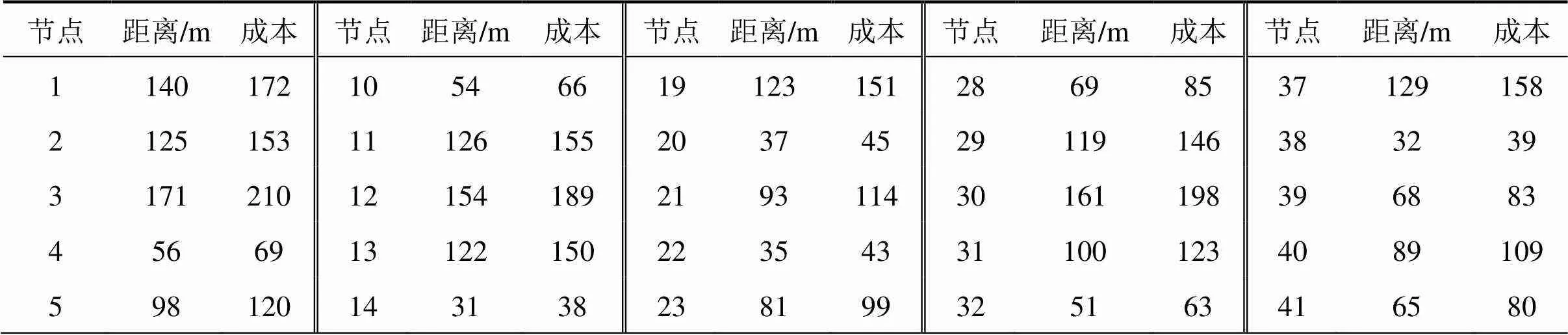
表1 每个节点的拥挤时路径成本

610012315133163244454333543425669 760741692113251111363488108432834 8951171732392682101356883443037 9951171811013527102125366883

2.3 路网中的路径选择表现

用Dijkstra算法来进行计算最小路径成本，从而得到行人移动方案，即行人的总路径。这里定义多边形的边界线是中途目的地，即为步行路上每个被选择的节点。用Microsoft Visual Atudio软件将C++代码实现此算法。结果如表2和图3所示。表2中的出口即为节点。最小路径为1，4，10，11，14，17，22，24，28，29，32，33，38，39，42，43和44。

图3 最小路径

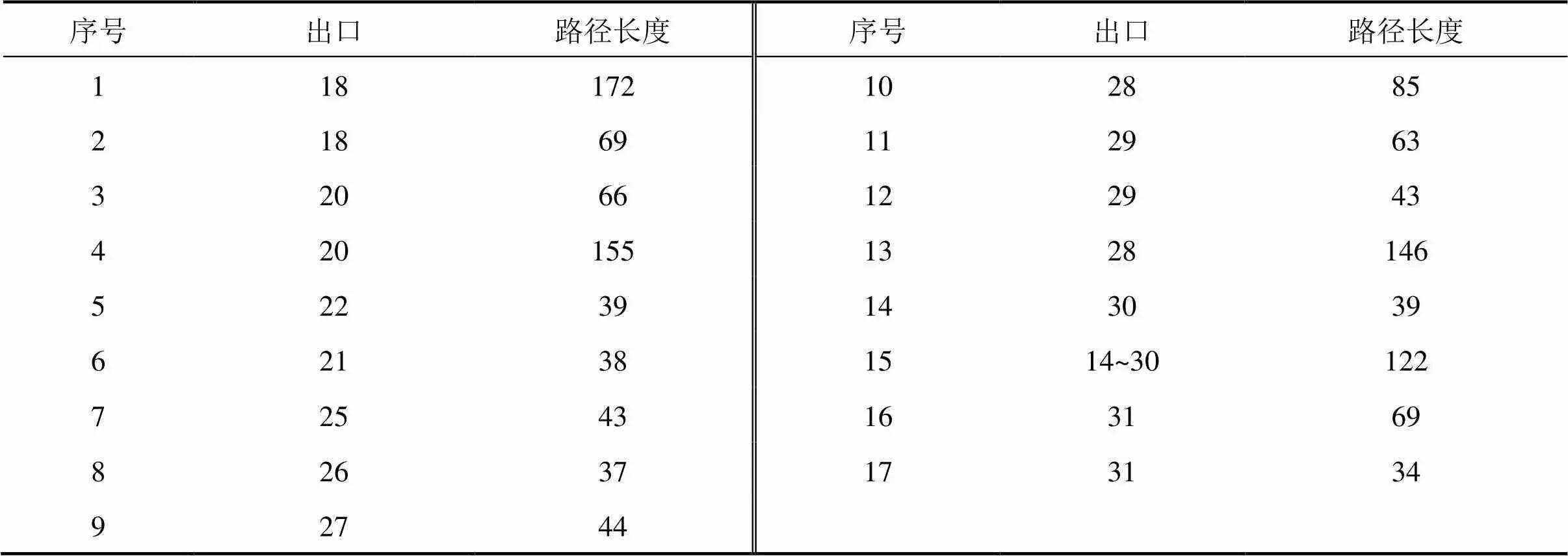
表2 最小路径

3 群体仿真研究

基于对个体行为的研究基础，研究群体紧急疏散行为。根据元胞自动机模型，结合实际情况，建立卢浮宫人群疏散模型。根据个体行为仿真研究设置相应的个体行为参数，利用pathfinder软件对卢浮宫人群疏散进行仿真分析。

3.1 元胞自动机模型

元胞自动机模型是一种把复杂系统简化的模型，可描述复杂现象。一个元胞自动机，由4部分组成：元胞、邻居、局部规则和元胞状态。它强大的建模和运算能力，在仿真中广泛运用。

以7×7网格系统的单出口疏散(如图4)为例，阐述疏散模型。疏散模型建立在大小为7×7元胞网格系统中，游客可移动区域为5×5网格。如图4有一格宽度缺口的区块为墙壁；中间小区块为游客，最大移动速度max=1个细胞/步。

3.1.1 参数计算

游客移动目的是安全出口，会尽可能地选择靠近出口的位置为下一移动目标。在计算方向参数时，首先计算游客到出口的安全距离，其次规定安全出口内距离为0。当行人所在位置不止一个安全出口时 , 游客离开最短距离为距最近安全出口的距离值；当安全出口的宽度大于一个元胞空格时，游客离开的最短距离为距安全出口内最近元胞的距离值[14]。元胞位置距安全出口的最短距离由下式计算：

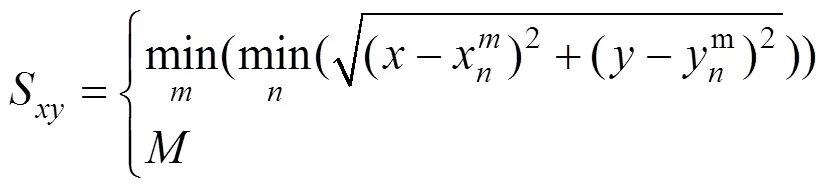
式中：Sxy为距安全出口最短的距离；(x,y)为元胞的坐标；为第m个门第n个元胞的坐标；M为很大的正数，故不用考虑墙的吸引力。

根据上文的个体仿真研究，将移动路径网络每个节点的拥挤时路径成本作为元胞位置距安全出口的最短距离。

3.1.2 移动规则

领域矩阵有8个可移动方向，见图5，较符合人群移动规律，故采用作为游客移动领域。

人群的疏散是一种相当复杂的现象，因此在实际仿真过程中，有着很大的难度。通过元胞自动机模型，能不断添加约束条件来获得新的概率转移矩阵，对疏散模型进行优化(图6)。

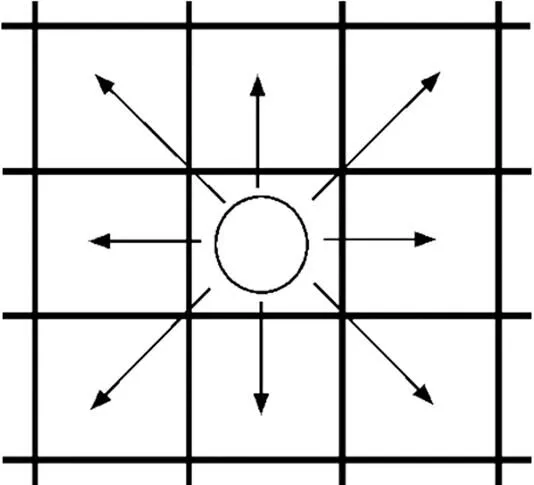
图5 游客移动领域

图6 概率转移矩阵

3.2 基于Pathfinder的卢浮宫疏散仿真

3.2.1 卢浮宫结构仿真环境参数

以卢浮宫结构较为复杂的Cour Marly为例，进行建模和仿真疏散。该区域有4个出口，均假设宽度为5 m：出口A，出口B，出口C，出口D。出口A位于转角处，相对位置较隐蔽，易造成人群堵塞的情况。出口B和出口C位置相对，紧急情况下有多种选择，情况相对来说稍乐观。出口D位于楼梯处，属于危险性较高的电子设备，极易引起人员紧急伤亡事故的发生，应引起重视。出口如图7~8所示。

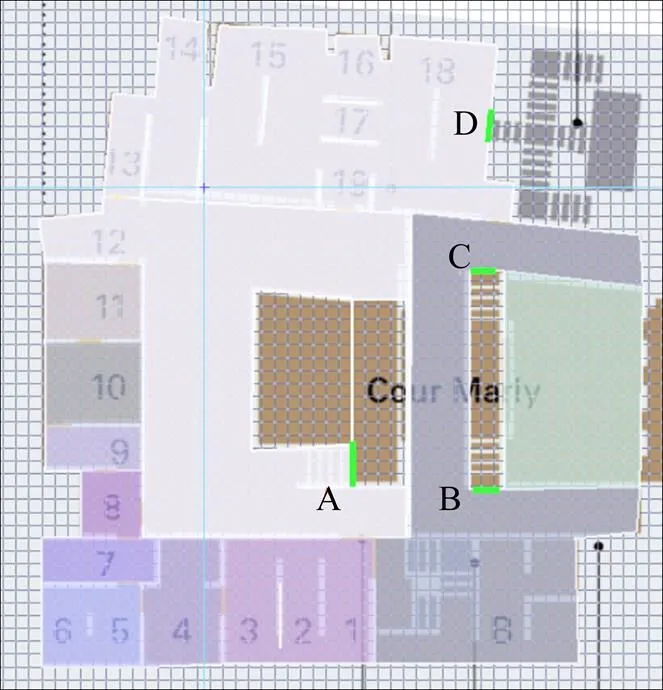
图7 俯视轮廓图

3.2.2 卢浮宫游客仿真环境参数

做如下假设：2018年卢浮宫接待游客超过810万，平均一天接约待22 300人，卢浮宫建筑物占地4.8 ha。假设紧急情况发生时，游客随机分布在0层。故人群密度为0.46 pers/m2。

3.3 分析可限制向出口移动的潜在瓶颈

以卢浮宫结构较为复杂的Cour Marly为例，进行建模和仿真疏散，寻找潜在的瓶颈。通过Pathfinder的密度参数，寻找不同级别的瓶颈。

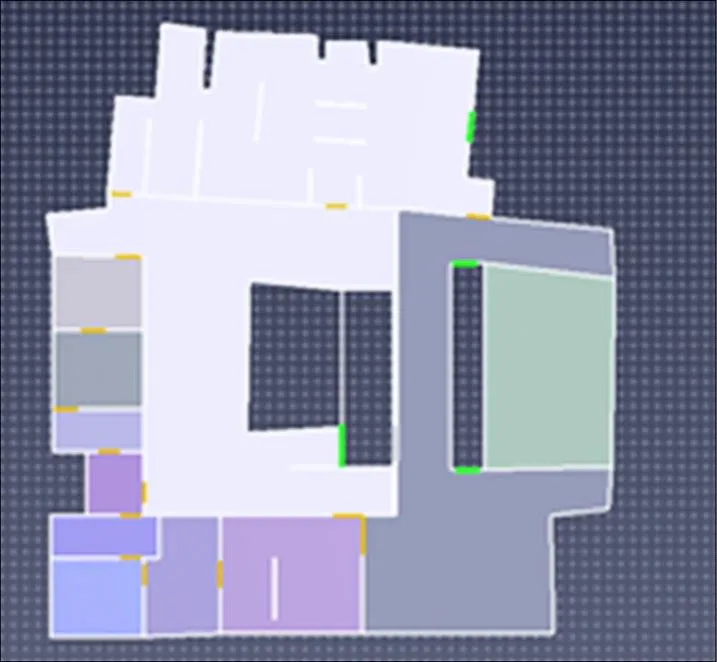
图8 Cour Marly的俯视轮廓图

图9 第10 s的人流拥挤情况

如图9所示，Cour Marly的白框区域均发生Ⅲ级至Ⅳ级的瓶颈现象。其产生原因大概分为以下 几类：

1) 交叉人流导致的瓶颈现象，如A区域。

2) 疏散通道上不合适的转角造成的瓶颈现象，如B和C区域。

3) 出口宽度的限制导致的瓶颈现象，如E和D区域。

4) 以上几种均是造成的原因，如F区域。

为了减少瓶颈现象，应尽可能采取以下措施：减少不同人流疏散路线的叠加；减少疏散通道上的转角；适当加宽人流较大的出口。

根据Cour Marly的白框区域发生Ⅲ级至Ⅳ级的瓶颈现象，找到卢浮宫拥堵进出口。进一步，对卢浮宫复杂部分进行局部仿真模拟，参数设置同上，找到展厅间疏散的拥堵通道。对卢浮宫整体仿真，通过局部与整体相结合，找出限制向出口移动的潜在瓶颈。

4 结论

1) 得出卢浮宫紧急疏散路径选择的方法。

2) 通过对卢浮宫复杂部分进行局部仿真模拟，找到展厅间疏散的拥堵通道；对卢浮宫整体仿真，找到卢浮宫拥堵进出口。通过局部与整体相结合，找出限制向出口移动的潜在瓶颈。

3) 为了减少瓶颈现象，给出应采取的措施。

在求最优疏散路径时，人在遇到危险时的心理因素、行为因素以及反应没有考虑在模型之中。因此，在今后的研究中，在突发事件下,紧急疏散策略的制定以及在设计最优疏散路径算法时，可以考虑这方面的因素。

[1] 姚刚, 陈宇翔, 石立国. 多发地震区超高层施工现场紧急疏散模型研究[J]. 施工技术, 2018, 47(24): 133−138. YAO Gang, CHEN Yuxiang, SHI Liguo. Research on emergency evacuation model of super high-rise construction site in multiple seismic areas[J]. Construction Technology, 2018, 47(24): 133−138.

[2] 胡丽娟, 姚加林, 郑亮. 基于NetLogo的地铁车站人员紧急疏散仿真研究[J]. 铁道科学与工程学报, 2017, 14(12): 2730−2737. HU Lijuan, YAO Jialin, ZHENG Liang. Simulation research on emergency evacuation of subway station personnel based on NetLogo[J]. Journal of Railway Science and Engineering, 2017, 14(12): 2730−2737.

[3] 孙超, 刘月婵, 王博, 等. 教学楼火灾蔓延及人员疏散的数值模拟[J]. 哈尔滨理工大学学报, 2018, 23(5): 106−112. SUN Chao, LIU Yuechan, WANG Bo, et al. Numerical simulation of fire spread and evacuation of teaching buildings[J].Journal of Harbin University of Science and Technology, 2018, 23(5): 106−112.

[4] 马建敏, 李晶, 雷福宝. 基于遗传算法的大型舰船紧急疏散路径规划[J]. 舰船科学技术, 2018, 40(10): 61−63. MA Jianmin, LI Jing, LEI Fubao. Emergency evacuation path planning for large ships based on genetic algorithm[J]. Ship Science and Technology, 2018, 40(10): 61−63.

[5] 李伟, 许强, 张颖. 轨道交通枢纽人员紧急疏散技术现状及展望[J]. 城市轨道交通研究, 2018, 21(4): 119−124. LI Wei, XU Qiang, ZHANG Ying. Current status and prospects of emergency evacuation technology for rail transit hubs[J]. Urban Rail Transit Research, 2018, 21(4): 119−124.

[6] SONG Weiguo, XU Xuan, WANG Binghong, et al. Simulation of evacuation processes using a multi-grid model for pedestrian dynamics[J]. Physica A: Statistical Mechanics and its Applications, 2005, 363(2): 492−500.

[7] Pursals Salvador Casadesús, Garzón Federico Garriga. Optimal building evacuation time considering evacuation routes[J]. European Journal of Operational Research, 2007, 192(2): 692−699.

[8] Takimoto Kouhei, Nagatani Takashi. Spatio-temporal distribution of escape time in evacuation process[J]. Physica A: Statistical Mechanics and its Applications, 2003, 320(320): 611−621.

[9] 刘雯丽. 城市轨道交通车站客流紧急疏散仿真研究[D].成都: 西南交通大学, 2013. LIU Wenli. Simulation study on emergency evacuation of passenger flow in urban rail transit stations[D]. Chengdu: Southwest Jiaotong University, 2013.

[10] FANG Weifeng, YANG Lizhong, FAN Weicheng. Simulation of bi-direction pedestrian movement using a cellular automata model[J]. Physica A: Statistical Mechanics and its Applications, 2003, 321(3): 223−225.

[11] 李得伟. 城市轨道交通枢纽乘客集散模型及微观仿真理论[D].北京:北京交通大学, 2007. LI Dewei. Passenger distribution model and microscopic simulation theory of urban rail transit hub[D]. Beijing: Beijing Jiaotong University, 2007.

[12] 付宇. 轨道站内行人移动模型与仿真[D]. 北京: 北京交通大学, 2012. FU Yu. Pedestrian movement model and simulation in orbital station[D]. Beijing: Beijing Jiaotong University, 2012.

[13] 吴贤国, 刘梦洁, 张立茂, 等. 地铁车站人群集散能力瓶颈风险评价[J]. 铁道标准设计, 2016, 60(2): 130−135. WU Xianguo, LIU Mengjie, ZHANG Limao, et al. Risk assessment of bottleneck capacity of metro station people[J]. Railway Standard Design, 2016, 60(2): 130− 135.

[14] 岳昊, 邵春福, 姚智胜. 基于元胞自动机的行人疏散流仿真研究[J]. 物理学报, 2009, 58(7): 4523−4530. YUE Hao, SHAO Chunfu, YAO Zhisheng. Study on pedestrian evacuation flow simulation based on cellular automata[J]. Acta Physica Sinica, 2009, 58(7): 4523− 4530.

Pedestrian emergency evacuation simulation study

WANG Wenyu1, WANG Xiliang1, LI Weimin2

(1. School of Transportation, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. Civil Engineering College, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

In recent years, the issue of safe evacuation of personnel in emergencies has received increasing attention. Avoiding major casualties and economic losses, and quickly and efficiently evacuating personnel has become an urgent problem to be solved. Therefore, based on the magnetic model, the motion behavior of the independent walking individual was investigated, and the path mobility benefit model was combined with the magnetic model and the social force model at the microscopic angle to approximate the pedestrian movement behavior in reality. Then, the individual pedestrian movement was promoted to group movement, and the evacuation model of the cellular automaton was proposed. The simulation was simulated in Pathfinder software by adding constraints and individual pedestrian movement parameter settings. The simulation results identify potential bottlenecks that limit the movement to the exit: bottlenecks caused by crossover flow; bottlenecks caused by inappropriate corners on the evacuation channel; bottlenecks caused by restrictions on exit width. And for the bottleneck phenomenon, give corresponding measures.

magnetic and social force combined model; Dijkstra algorithm; cellular automata; Pathfinder simulation

U1

A

1672 − 7029(2019)08− 2130 − 07

10.19713/j.cnki.43−1423/u.2019.08.033

2019−03−12

河北省重点研发计划项目(18275406D)；河北省交通运输厅科技项目(Y-201601)；河北省高等学校科学技术研究重点项目(2016120)

王希良(1966−)，男，山东平度人，教授，博士，从事交通运输规划方面的教学科研工作；E−mail：wangxiliang263@sina.com

(编辑 阳丽霞)