基于CCLPSO算法的Y型交路列车开行方案优化研究

谭丽，韦子文

基于CCLPSO算法的Y型交路列车开行方案优化研究

谭丽，韦子文

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

列车开行方案通常包括列车停站方案、交路计划以及编组方案，是地铁组织运输的基础。结合交通运输组织的实践经验以及输送能力与客流需求达到最佳匹配的原则，以乘客出行成本及企业运营成本最低为目标，综合考虑线路最大通过能力、最小发车频率和最大可用车底数量等限制条件，构建城市地铁Y型交路模式下的列车开行方案优化模型，来确定Y型交路模式列车开行方案的主线及支线的列车运行区段及各线的列车开行频率。采用分类学习混合粒子群算法(CCLPSO)对其进行求解，通过实际案例验证了模型的合理性和算法的有效性，并对折返站位置和列车开行频率进行灵敏度分析。研究结果表明：Y型交路的折返站的选取对乘客出行成本影响显著，相比于其他2种算法，采用该算法可使综合成本分别减少16.9%和31.6%。

城市轨道交通；列车开行方案；混合粒子群算法；分类学习

在城市轨道交通发展过程中，由于城市形态、重大项目的建设及城市的多点战略布局[1]等原因，逐渐形成了除传统的单一交路运行模式外的大小交路、衔接交路等多交路运行模式，Y型交路运行模式即是其中一种特殊的交路形式。针对列车在各种交路运行模式下以何种开行方案运行这一问题，国内外学者进行了诸多研究。王永亮等[2]采用遗传模拟退火算法求解以运营网络系统最佳为目标的列车运行交路计划双层模型；朱宇婷[3]研究编制列车开行方案的各项影响因素，分别以单条线路和整个运营网络作为研究对象，建立列车运行交路模型并提出城市轨道交通列车开行方案的优化方法；Szetoa等[4]研究了近郊区公交车的运行交路和发车频率的问题，采用改进的遗传算法对所建立的以乘客出行时间最短和乘客换乘次数最少为目标的双目标优化模型；Chang等[5]构建高速铁路列车交路方案双目标优化模型，用模糊数学的方法将其转化为单目标优化模型，并选取台湾某高铁线路验证了模型的有效性；陈玥[6]综合考虑列车满载率和线路通过能力等约束，设计了遗传模拟退火算法求解以乘客总候车时间最短为目标的交路方案模型。由于遗传算法[7]具有较好的全局寻有能力、鲁棒性高且容易与其他算法结合的特点，与粒子群算法结合(以粒子群算法为主体)可克服其收敛速度慢、局部搜索能力差等缺点，同时引入分类学习[8]的思想有利于求解离散类优化问题，很适合在城市轨道交通这一离散事件动态系统[9]中应用。综上，对城市轨道交通Y型交路的列车开行方案的研究相对匮乏。本文参考研究大小交路[10−15]的方法，构建城市轨道交通Y型交路列车开行方案优化模型，采用分类学习混合粒子群算法对其进行求解并验证模型的合理有效性。

1 问题描述

目前，我国采用Y型交路模式运行的城市轨道交通线路有广州地铁3号线、上海地铁10号线和11号线等，且都仅以如图1所示的2种开行方式运行。在支线独立运营形式中，支线交路上的列车仅在支线(如虚线所示)上行驶；支线全直通运营形式中，支线交路上的列车与主线交路上的列车在部分区段共线行驶。

(a) 支线独立运营形式示意图；(b) 支线全直通运营交路形式示意图

随着线路上客流分布特征愈发不均衡，当前这2种开行方案在高峰时段可能造成乘客等待时间过长、企业运营成本大幅增加等问题。针对以上问题，本文对Y型交路上支线的折返站位置及主、支线上列车的开行频率组合优化，以使线路上客流需求和运输能力达到最佳匹配。

2 建模

本文综合考虑乘客和运营企业双方的利益，构建以乘客等待时间最短、列车走行公里最短和列车运用数量最少为目标的Y型交路列车开行方案优化模型。如图2所示，首先对线路上的各车站编号，主线依次从1编到，支线紧跟由+1编到。其中，a为待优化的支线交路的折返站位置，b为Y型交路主线和支线的接轨站。其中，主线、支线上的列车分别如实线、虚线所示的线路以各自的开行频率行驶，且2条交路上的列车在[a, b]区段共线 行驶。

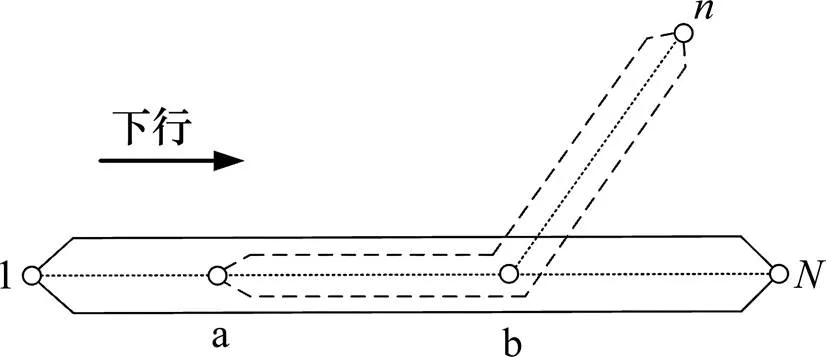
图2 Y型交路基本模型

2.1 模型基本假设及函数定义

根据Y型交路运营模式特点，做出如下假设：

假设1 Y型交路列车均采用站站停车的停车方案；

假设2 考虑乘客出行偏好，乘客会优先选择直达线路，并且不考虑乘客滞留情形；

假设3 车底周转方式独立运用，并且列车选型相同；

假设4 考虑列车运营组织的复杂性，各断面的交路覆盖层数最大为2；

假设5 在研究时段内，主、支线各自的发车间隔不变，并且上、下行列车成对开行。

为方便描述，本文对以下几项函数做以下 定义：

1和2分别表示主、支线交路的列车开行频率；

2.2 乘客出行成本

乘客出行成本主要由乘客的等待时间成本来表征，包括在途等待时间及候车等待时间，如式(1)所示。

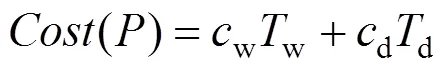
式中：w和d表示候车等待时间和单位在途等待时间的单位时间价值；w和d表示乘客候车等待时间和在途等待时间。

在途等待时间指的是各OD客流运行经过的各区间运行时间及在所经过各车站的停站时间之和。

由于城市轨道交通行车密度大，行车间隔短，乘客到达独立于列车到达时刻，呈现随机正态分布。既有研究表明：在列车行车间隔较短(一般小于10 min时)的条件下，线路上客流的平均候车等待时间趋近于行车间隔的一半。

故Y型交路主线(除主线与支线共线区段以外)上行乘客和下行乘客的候车等待时间分别如式(2)~ (3)所示：

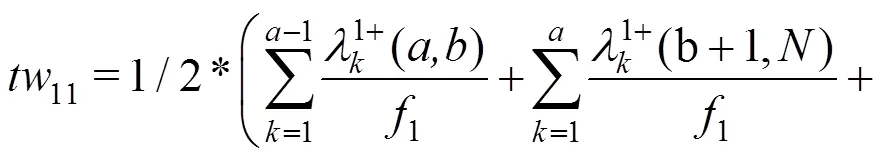
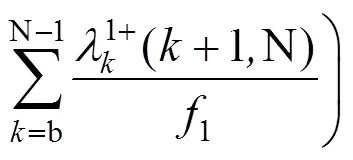
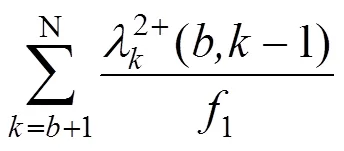
Y型交路支线(除主线与支线共线区段以外)上行乘客和下行乘客的候车等待时间分别如式(4)~(5)所示：

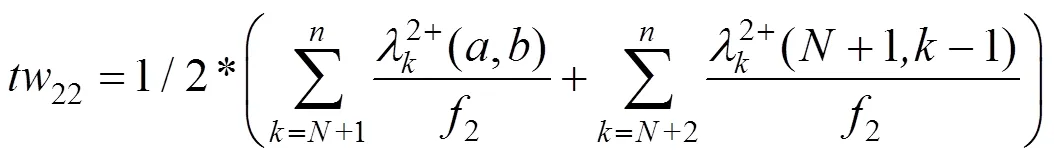
Y型交路主线与支线共线区段上的乘客和换乘客流的候车等待时间如式(6)~(7)所示：

故线路上乘客的总候车等待时间为式(2)~(7) 之和。

2.3 企业运营成本

企业运营成本主要可以分为固定成本(指车辆购置成本)及变动成本(主要由列车走行公里数决定)2部分。企业运营成本如式(8)所示：

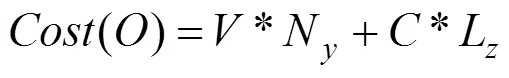
式中：为单位列车购置费用；为单位列车运营耗费成本；N为所需列车数量；L为研究时段内列车总走行公里数。

2.3.1 车辆购置成本

运营所需列车数量可由式(9)求得：

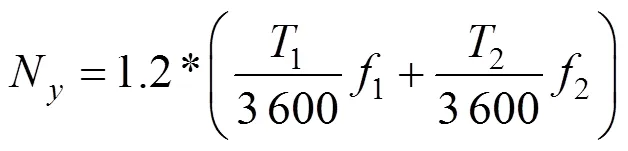
式中：1和2分别表示主线、支线的列车周转时间；乘以系数1.2是考虑了车辆维护等所必需的备 用车。

2.3.2 列车运行耗费成本

列车总走行公里数可由式(10)求得：

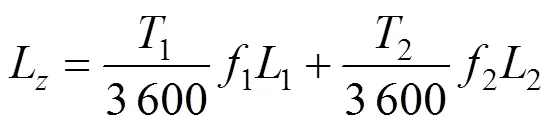
式中：1和2分别表示主线、支线交路的长度。

2.4 优化模型及约束

本文采用理想点法将多目标优化问题转化为单目标优化问题。构建优化模型如式(11)所示：

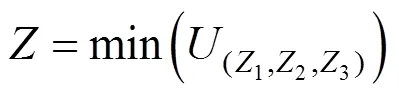
对城市轨道交通Y型线路列车开行方案的影响因素进行分析，它对该模型构成如下几个约束条件：

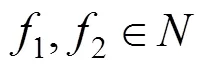
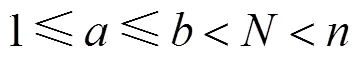
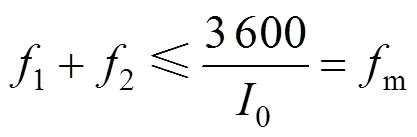
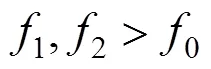
约束条件中，式(13)~(14)为基本约束，规定了折返站的位置及开行频率的整数约束；式(15)是为了满足列车最小追踪间隔；式(16)是为了满足最小发车频率的限制；式(17)为运用列车数量的约束。综上，该模型为多目标优化模型，各目标之间存在矛盾关系。如果侧重考虑乘客的利益，乘客出行成本降低的同时，列车开行频率及所需列车数必然增加；如果侧重考虑运营企业的利益，则地铁运输服务差，严重影响乘客出行。

3 分类学习混合粒子群优化算法

3.1 标准粒子群算法

粒子群(PSO)算法通用性强，控制参数少，操作简单等优点，与传统的数学规划方法相比具有不可比拟的优势。

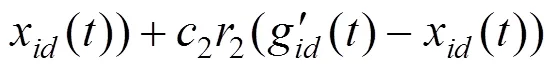
3.2 分类学习混合粒子群算法

首先，以PSO算法为主体，混合(Commix)遗传算法中的交叉、变异策略来解决其搜索中后期收敛速度变慢和“早熟收敛”等问题。其次，由以上所建立的Y型交路列车开行方案优化模型可知，它属于典型的离散、动态多目标优化问题，根据参考文献[8]，引入“分类学习”(Clssified Learning)思想，不仅增加了粒子种类的多样性，而且能获得良好的收敛特性。以下将该改进的算法称为分类学习混合粒子群算法(Commix Classified Learning PSO)。

根据大量数值实验计算，粒子种群将按1:1:2的比例划分为“好”、“中”和“差”3类，并根据各自的学习策略更新粒子速度，粒子位置更新公式与标准PSO算法相同。具体更新公式如式(20)~(22)所示。

同时采用惯性权重对数递减的策略代替以往线性递减的策略，以更好地反映粒子的真实搜索过程，2个学习因子1和2也分别动态变化以平衡算法的全局搜索和局部搜索能力。

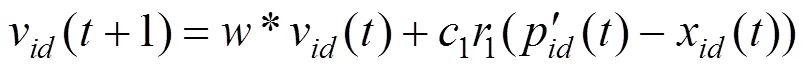
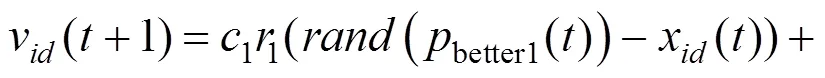
在采用分类学习混合粒子群算法优化Y型交路列车开行方案过程中，每个粒子都是3维的，其速度、位置表示方法与标准粒子群算法相同，各维变量分别表征折返站位置，主/支线的开行频率1和2对/h。

3.3 算法求解流程

该改进算法的求解流程如图3所示。

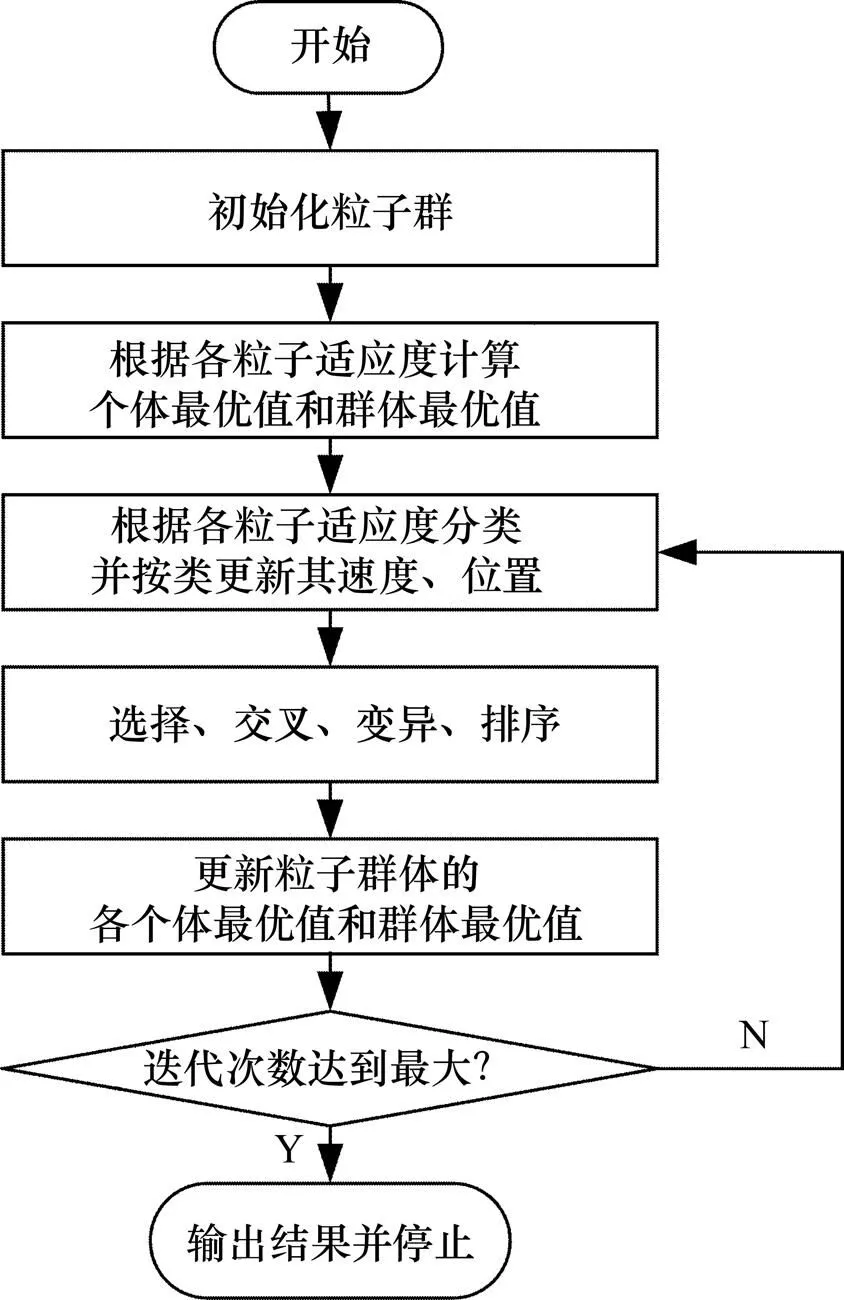
图3 算法流程图

3.4 数值试验

选取Sphere, Noise Quadric和Rastrigin这几个测试函数以测试算法的综合性能，并与混沌粒子群(CPSO)算法和遗传−粒子群(GAPSO)算法对比。其中，Sphere为单峰值函数，Noise Quadric函数中有随机参数，可被看作含有离散问题的函数， Rastrigin函数为多峰值函数。

算法的参数设置如下：粒子群数目设置为40，维数设置为3，最大迭代次数设置为500。对比结果分别如图4~6所示。

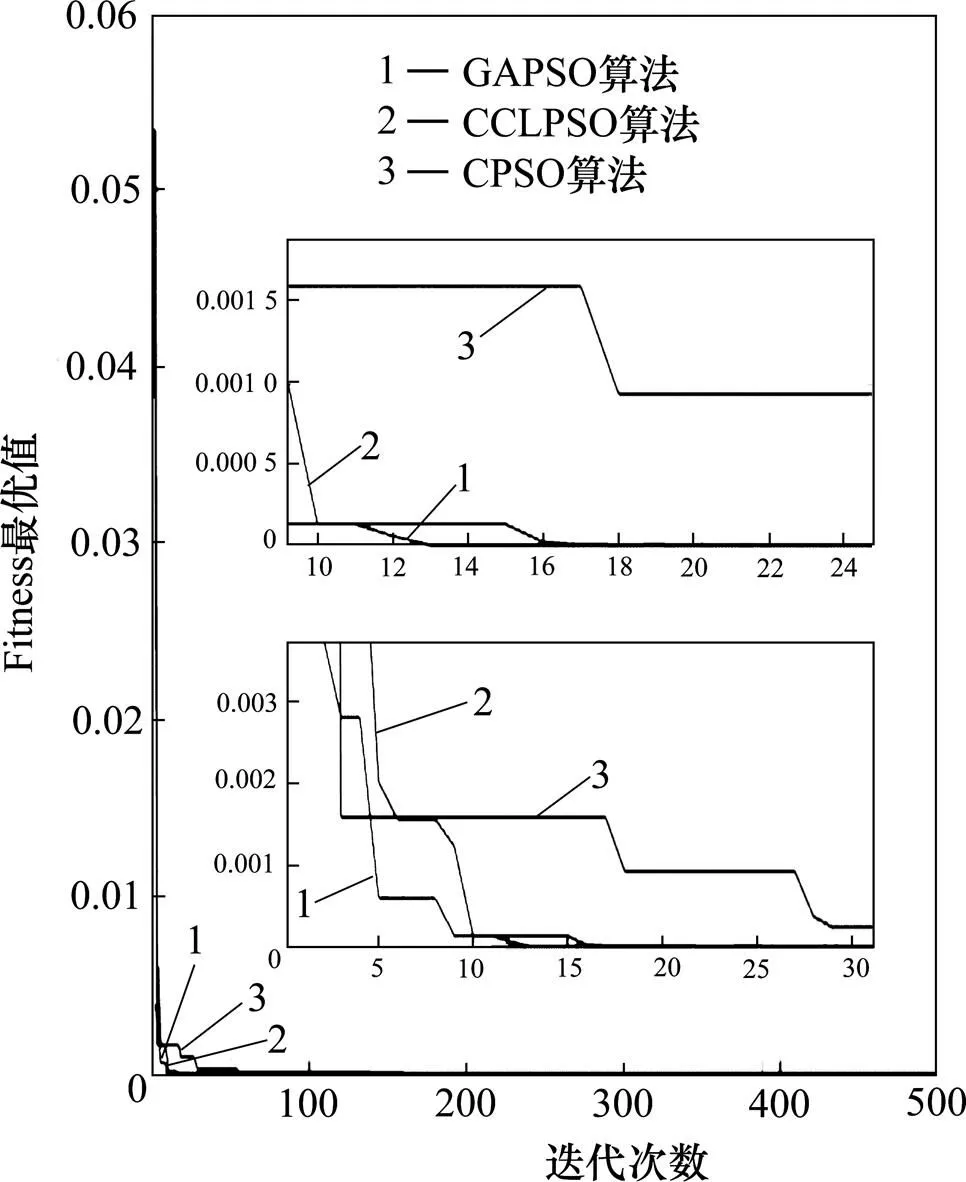
图4 Sphere函数全局最优曲线图

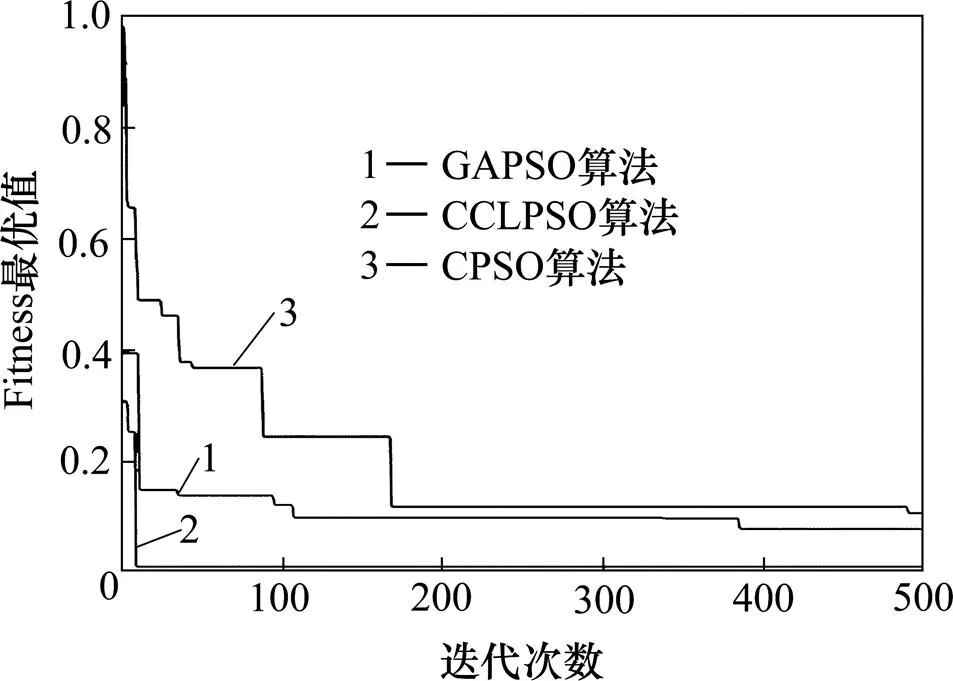
图5 Noise Quadric函数全局最优曲线图

由以上对比结果可知，CCLPSO具有较快的收敛速度和求解精度。

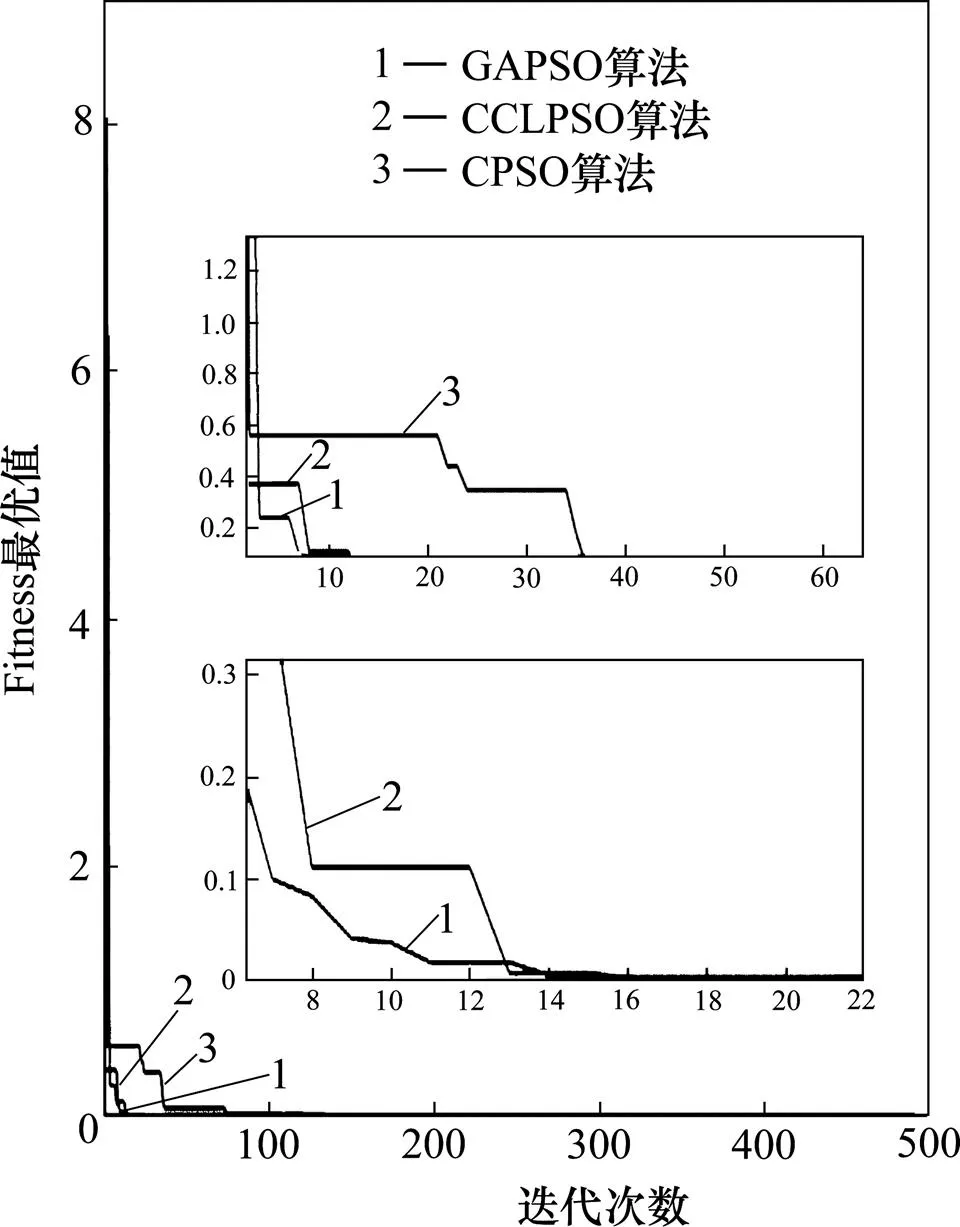
图6 Rastrigin函数全局最优曲线图

4 案例研究与仿真

4.1 参数设置

以某城市轨交通线路为例，该轨道交通线上共设31座车站，线路全长约36 km。对线路上31座车站按先主线后支线的方法进行编号,且研究时段的列车运行参数及线路参数已知。模型中各参数的定义如表1所示。

表1 模型参数符号及定义

4.2 优化流程及案例求解

Y型交路列车开行方案优化流程如图7所示。

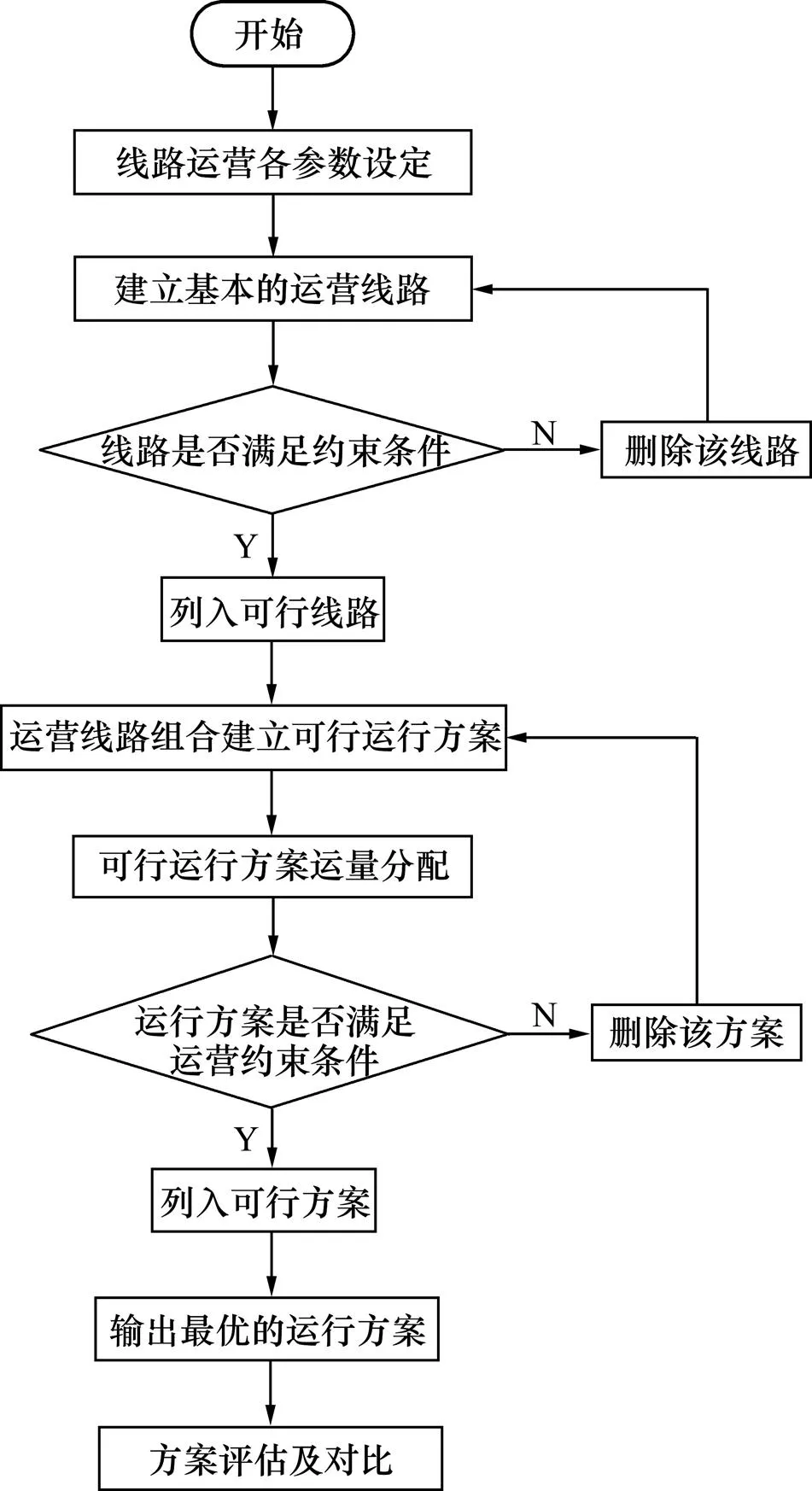
图7 案例优化流程图

如图7，首先，对线路上的客流量进行调查分析，并设定模型的主要控制参数；其次，根据Y型交路的特点以及模型的约束条件，先后形成可行线路集、可行方案集；最后，采用改进的算法在可行解集中寻求最佳列车开行方案，并对该方案进行评估及对比。

通过Matlab软件编程，对上述模型进行求解。表2为用GAPSO，CPSO和CCLPSO算法分别优化交路方案时的仿真对比结果，包括3个决策变量(折返站位置，主/支线的开行频率1和2对/h)和2个中间量(乘客候车等待时间w分钟及列车走行公里数zkm)及综合成本Fitness。

由表2可知，在对第2节所述多目标模型优化时，与另外2种算法相比较，CCLPSO算法使综合成本分别减少约16.9%和31.6%，结果表明：CCLPSO具有较好的寻优性能，极大地优化了该轨道交通线路的列车开行方案，使线路上客流需求与运力资源达到更好地匹配。

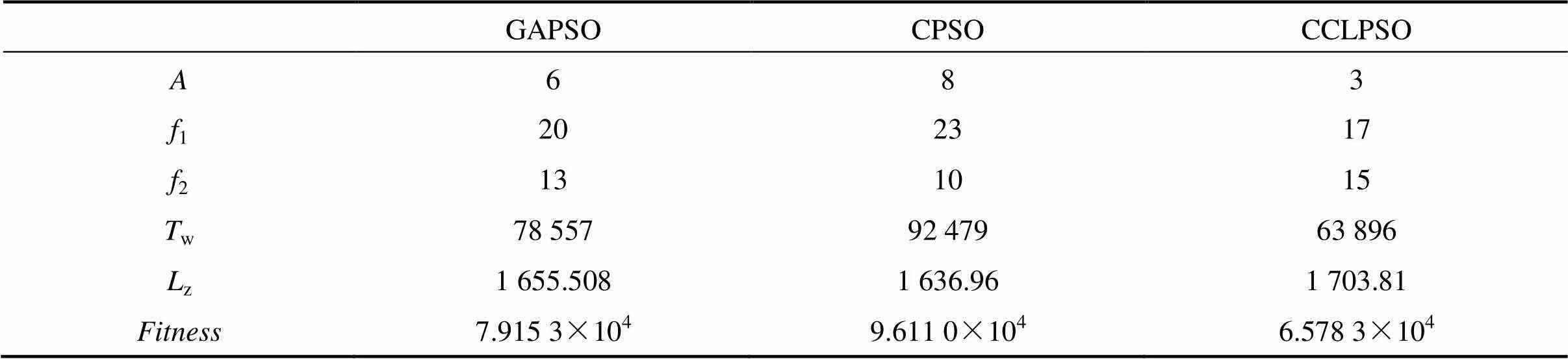
表2 各算法优化方案对比

4.3 灵敏度分析

采用控制变量法对折返站位置的灵敏度进行分析，结果分别如图8~9所示。

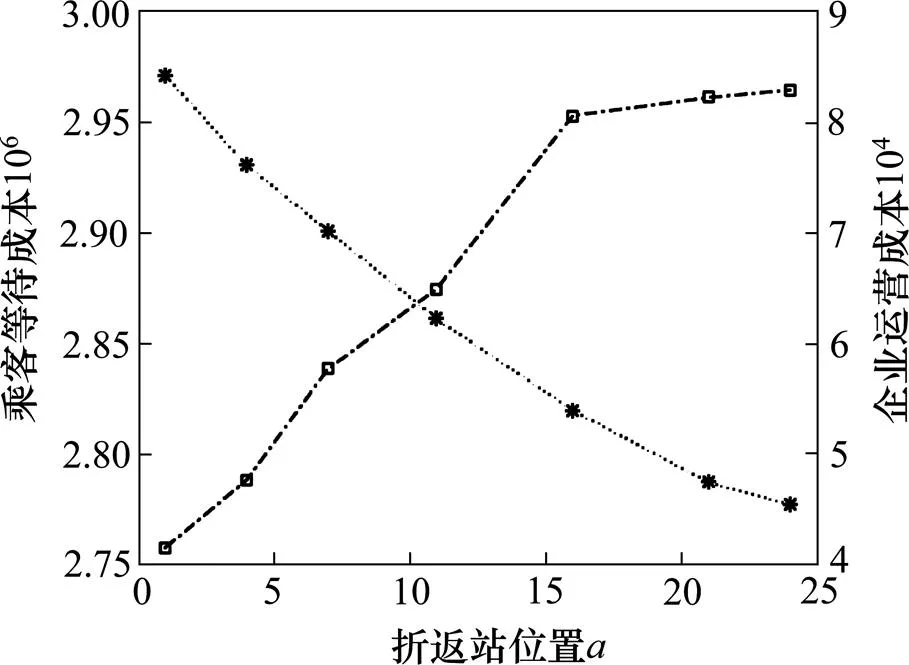
图8 折返站位置灵敏度分析

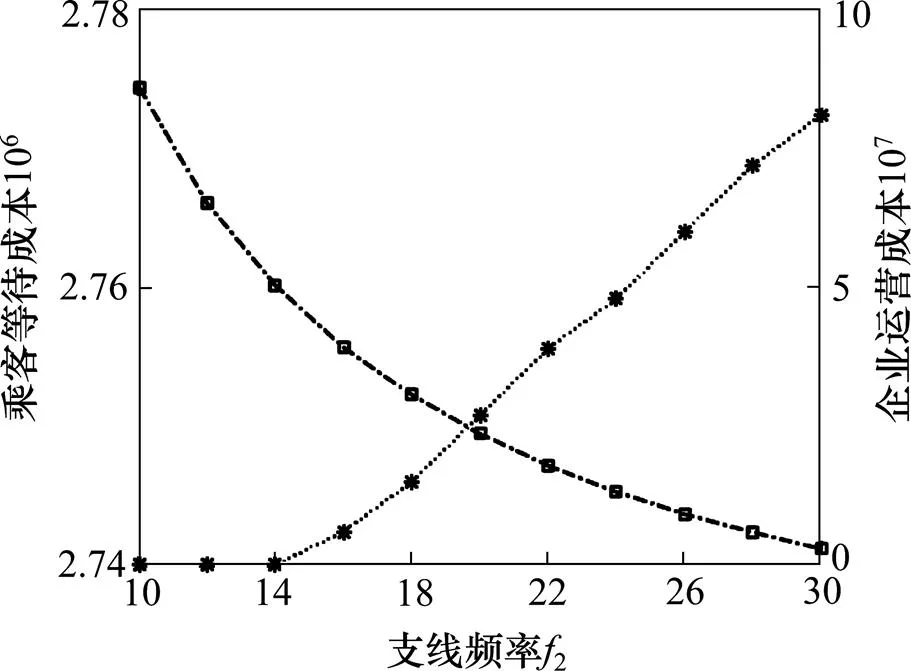
图9 支线频率灵敏度分析

由图8~9可知，折返站的位置对乘客出行成本影响较大，折返站设置得越靠后，乘客出行成本增加越大，当折返站设置在第17站及以后位置时，乘客出行成本的增加才趋于平缓；支线上列车的开行频率在大于15对/h时，企业运营成本开始逐渐增加。

5 结论

1) 根据Y型交路的运营模式建立交路的列车开行方案多目标优化模型。

2) 设计分类学习混合粒子群算法(CCLPSO)求解该模型。

3) 结合实际案例验证模型及算法是可行有效的。在综合考虑乘客和运营企业双方利益求解优化模型时，与GA-PSO算法和CPSO算法相比较，用CCLPSO算法求解效果更佳，综合成本分别减少16.9%和31.6%。为地铁运营企业列车开行方案的编制提供新的技术参考。

[1] 刘猛. 城市轨道交通Y型线路列车交路方案研究[D].北京: 北京交通大学, 2017. LIU Meng. Analysis on the train routing scheme of Y-type urban rail line[D]. Beijing: Beijing Jiaotong University, 2017.

[2] 王永亮, 张星臣, 蒋洋, 等. 城市轨道交通网络运营鲁棒性[J]. 北京工业大学学报, 2013, 39(7): 1014−1019. WANG Yongliang, ZHANG Xingchen, JIANG Yang, et al. Urban rail transit network operation robustness[J]. Journal of Beijing University of Technology, 2013, 39(7): 1014−1019.

[3] 朱宇婷. 考虑乘客出行效率的城市轨道交通列车开行方案优化研究[D]. 北京: 北京交通大学, 2016. ZHU Yuting. An optimization research for train plan of urban rail transit with the consideration of passengers’ travel efficiency[D]. Beijing: Beijing Jiaotong University, 2016.

[4] Szetoa W Y, WU Yongzhong. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong[J]. European Journal of Operation Research, 2011, 209: 141−155.

[5] Chang Y H, Yeh C H, SHEN C C. A multi-objective model for passenger train services planning application to Taiwan’s High-speed Rail Line[J]. Transportation Research Part B, 2000, 34(2): 91−106.

[6] 陈玥. 城市轨道交通列车运行交路方案研究[D]. 北京:北京交通大学, 2016. CHEN Yue. Study on train routing scheme of urban rail transit[D]. Beijing: Beijing Jiaotong University, 2016.

[7] 雷明, 孟学雷. 基于协同进化遗传算法的高速铁路运行调整研究[J]. 铁道科学与工程学报, 2017, 14(6): 1138−1142. LEI Ming, MENG Xuelei. High-speed railway operation adjustment based on co-evolutionary genetic algorithm[J]. Journal of Railway Science and Engineering, 2017, 14(6): 1138−1142.

[8] 张凯, 宋锦春, 李松, 等. 基于分类学习粒子群优化算法的液压矫直机控制[J]. 机械工程学报, 2017, 53(18): 202−204. ZHANG Kai, SONG Jinchun, LI Song, et al. Hydraulic straightener control optimizer based on particle swarm with classification learning[J]. Journal of Mechanical Engineering, 2017, 53(18): 202−204.

[9] 李爱菊. 城市轨道交通系统的极大代数模型研究[D].北京: 北京交通大学, 2006. LI Aiju. Study on the maximum algebraic model of urban rail transit system[D]. Beijing: Beijing Jiaotong University, 2006.

[10] 许得杰, 毛保华, 雷莲桂. 城市轨道交通大小交路列车开行方案优化研究[J]. 交通运输系统工程与信息, 2017, 17(1): 120−126. XU Dejie, MAO Baohua, LEI Liangui. Optimization for train plan of full-length and short-turn routing in urban rail transit[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 120−126.

[11] Cadarso L. Integration of timetable planning and rolling stock in rapid transit networks[J]. Annals of Operations Research, 2012, 199(1): 113−135.

[12] 王媛媛, 倪少权. 城市轨道交通大小交路模式列车开行方案的优化[J]. 铁道学报, 2013, 35(7): 1−7. WANG Yuanyuan, NI Shaoquan. Optimization of train schedules of full-length & short-turn operation modes in urban rail transit[J]. Journal of the China Railway Society, 2013, 35(7): 1−7.

[13] 田晟, 马美娜, 杨锦明. 基于大小交路优化的地铁行车组织方案[J]. 交通信息与安全, 2017, 35(1): 112−117. TIAN Sheng, MA Meina, YANG Jinming. An organizational scheme for metro traffic based on long-short route optimization[J]. Traffic Information and Safety, 2017, 35(1): 112−117.

[14] Alejandro T, Cristian E, Sergio J D. Optimal design and benefits of short turning strategy for a bus corridor[J]. Transportation, 2011, 38(1): 169−189.

[15] Canca D, Barrena E, Laporte G, et al. A short-turning policy for the management of demand disruptions in rapid transit systems[J]. Annals of Operations Research, 2016, 246(1/2): 145−166.

Optimization research of train schedule of Y-type train routing mode based on CCLPSO algorithm

TAN Li, WEI Ziwen

(School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

The train schedule usually includes train stop schedule plan, routing scheme and formation scheme. It is the basis of subway transportation. Combining the practical experience of transport organizations and the principle of the best match between transport capacity and passenger flow demand, taking the minimum value of passenger travel costs and corporate operating costs as the goals, considering the constraints of maximum rail capacity, minimum departure frequency and maximum available electric multiple units, a optimization model for city subway Y-type operation mode is constructed to determine the operation section of mainline and branch line and the train frequency on both lines in the Y-type operation mode. The commix classified learning particle swarm algorithm (CCLPSO) was used to solve the model. The rationality of the model and the effectiveness of the algorithm were verified by a practical case, and the sensitivity analysis of the turn-back station and frequency were conducted. The results show that the selection of turn-back station affects the cost of waiting time of passengers significantly, the comprehensive cost can be reduced by 16.9% and 31.6% by comparing with the other two algorithms, respectively.

urban rail traffic; train schedule; commix particle swarm algorithm; classified learning

U2-9；TP312

A

1672 − 7029(2019)08− 2122 − 08

10.19713/j.cnki.43−1423/u.2019.08.032

2018−11−23

甘肃省教育厅自然科学基金资助项目(2017A-020)；中国铁路总公司科技研究开发计划项目(2017J012-A)

谭丽(1962−)，女，辽宁海城人，副教授，从事交通信息工程及控制研究；E−mail：2403323264@qq.com

(编辑 阳丽霞)