结合单元试验数据的指数型串联系统定时截尾试验可靠性评估方法

金俊坤， 杨宁国， 吕冬雪

(63850部队， 吉林 白城 137001)

0 引言

武器装备可靠性试验一般会产生两部分数据：一部分是以各组成分系统或部件独立工作为基础产生的单元可靠性试验数据(以下简称单元试验数据)；另一部分是以全部单元组装成完整结构进行试验而产生的系统可靠性试验数据(以下简称系统试验数据)。以往的可靠性评估方法只统计系统试验时间，而忽略独立开展的各单元试验时间，各单元故障数计入系统试验故障数中或者舍弃掉，前者试验方法十分严苛，但单元故障和系统故障来自不同的试验环境，直接相加有些欠妥，容易引起争议；后者未充分利用单元试验信息，产生数据浪费。综合利用单元试验数据可提高武器装备的可靠性评估精度，尤其在系统试验数据不足情形下，如射击实弹数不足以评估弹药可靠性时，利用独立开展的单元可靠性试验数据或其他性能试验形成的单元试验数据，在一定程度上可以补充实弹数的不足。

关于单元信息的利用问题，刘春和等[1]、孙怀义[2]和柳超[3]均针对定数截尾方案给出了单元试验数据的折合公式，但鲜有文献讨论定时截尾情况，原因是此时试验时间和故障率没有精确的概率分布函数。

考虑到武器装备试验中经常采用便于计划和管理的定时截尾试验方案，本文针对定时截尾情况，基于指数型串联系统模型，通过引入定时截尾试验方案下失效率的近似Fiducial概率密度，将单元试验时间和故障数折合到系统可靠性意义下的等效试验时间和故障数，用等效试验数据与系统试验数据一起来评估被试武器装备的平均故障间隔时间(MTBF)。分析表明，定时截尾和定数截尾二者利用单元信息的公式是有差异的，有些文献在定时截尾情况下仍然套用定数截尾的单元信息折合公式是值得商榷的。

1 指数型串联系统

机电类武器装备的单元服从指数分布，整个系统也服从指数分布，如果某一个单元出现故障，就会导致整个系统工作异常，在此种情况下可以认为被试武器装备为指数型串联系统。

设系统由m个不同的相互独立单元串联组成，第i个单元的寿命为Ti，可靠度为Ri(t)=P(Ti>t)(i=1,2,…,m),各单元发生故障互相独立，即T1,T2,…,Tm相互独立，串联系统寿命T=min(T1,T2,…,Tm)，系统可靠度R(t)为

(1)

式中：λi(t)为第i个单元的失效率。

由(1)式可知串联系统的失效率为

(2)

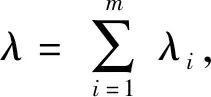
2 单元可靠性试验数据的折合

组成指数型串联系统的m个单元在独立试验时，产生的单元试验数据为(r′i,T′i)，其中r′i为第i个单元在独立试验时的故障次数，T′i为第i个单元独立试验时间。在完整结构下试验时，产生的系统试验数据为(r′,T′)，其中：r′为系统试验时的故障次数，T′为系统试验时的试验时间。

如果能够将单元试验数据(r′i,T′i)依据一定法则折合成等效的系统试验数据，就能够达到充分利用单元试验数据的目的。

对于定时截尾试验，试验截止时间T′不是失效时刻，但由指数分布性质可知,当试验总故障数为r′时，统计量2λT′介于2λTr′和2λTr′+1之间，而2λTr′服从自由度2r′的χ2分布，2λTr′+1服从(2r′+2)的χ2分布，即2λTr′～χ2(2r′),2λTr′+1～χ2(2r′+2)，因此采用Cox的建议[4]，近似认为2λT′～χ2(2r′+1)，由此得到定时截尾情况下失效率λ的Fiducial概率密度函数[5]为

(3)

式中：f(λ)为系统失效率λ的Fiducial概率密度函数；Γ(x)为伽马函数；Γ(y|a,b)表示已知a和b条件下y服从伽马分布。

对于指数型串联系统组成系统的m个单元，每个单元也同样有2λiT′i～χ2(2r′i+1)，单元失效率λi的Fiducial概率密度函数为

(4)

式中：fi(λi)为λi的Fiducial概率密度函数。

由(4)式，可得λi的均值和方差分别为

(5)

(6)

式中：

(7)

假设这m个单元根据单元试验数据(r′i,T′i)折合成系统可靠性意义下的等效故障数为r″和等效试验时间为T″，则由等效数据(r″,T″)可得系统失效率λ的均值和方差分别为

(8)

(9)

从串联系统角度出发，由(2)式得到各单元失效率λi和系统失效率λ的关系，即

(10)

(11)

由(5)式～(11)式，按均值相等和方差相等建立折合方程组:

(12)

解此方程组，得r″和T″分别为

(13)

(14)

对于(13)式和(14)式，需要特别说明的是：

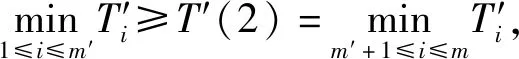
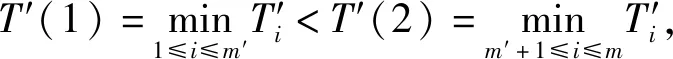
T′i(2)=T′(1)，

(15)

r′i(2)=(T′(1)/T′i)×r′i，

(16)

式中：r′i(2)、T′i(2)为单元i的信息压缩后数据(i=m′+1,…,m)。

由(13)式、(14)式，得到由单元试验数据折合到的等效故障数r″和等效试验时间T″，再加上系统试验数据中的故障数r′和试验时间T′，就得到总故障数和试验总时间，即

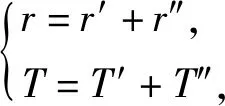
(17)

式中：r为总故障数；T为试验总时间。

有了(r,T)，就可依据国家军用标准GJB899A给出MTBF点估计值和区间估计[θL,θU]或单侧置信下限[11]，此处不再复述。

对于定数截尾情况，统计量2λT′～χ2(2r′)，由此得到定数截尾情况下失效率λ的Fiducial概率密度函数[2]为

(18)

由(18)式仿照定时截尾情况的推导过程，可得到定数截尾情况下的单元试验数据折合公式，推导过程不再赘述，直接给出折合结果：

(19)

(20)

若出现某个单元故障数为0情况，则参照定时截尾折合方法的特别说明内容进行数据压缩处理。(19)式和(20)式是大多数文献利用单元信息的折合公式，这两个公式与(13)式、(14)式是有差异的，直接将(19)式和(20)式应用到定时截尾情况，将会导致折合误差。

3 实例计算

某型装甲车辆火控系统可靠性试验采用定时截尾方案，规定的系统试验总时间为390.0 h. 该火控系统由9个单元组成，单元和系统可靠性试验数据如表1所示。

表1 某火控系统单元和系统可靠性试验数据

以往的MTBF估计方法是只统计全部单元同时参与试验的系统试验时间，即只计390.0 h,将独立开展的单元试验故障数直接计入系统故障数，则故障数为5，因此MTBF的点估计值=390.0 h/5=78.0 h，置信度80%下的单侧置信下限为49.3 h. 这种可靠性数据处理方法有一个问题：单元试验数据和系统试验数据是在不同环境下取得的，单元的2个故障在数值上也不一定等效于系统的2个故障，单元故障数直接和系统故障数相加作为试验总故障数存在不合理性，局部不可能直接等效于总体。

为科学合理地利用单元试验数据，首先采用(13)式和(14)式进行单元数据等效处理，则单元试验数据等效的系统试验时间为39.5 h，等效故障数为2.3；再结合系统试验时间和故障数，由(17)式得到总试验时间为429.5 h和总故障数为5.3，由此得到该火控系统的MTBF点估计值为81.0 h，同样在置信度80%下的单侧置信下限为52.0 h.

上述评估过程表明：

1)由折合公式得到单元的2个故障等效于系统的2.3个故障，进一步验证了将单元故障数直接和系统故障数相加是不合理的，同时单元数据向系统数据等效后，不能简单认为故障数一定减少。

2)各单元试验时间有长有短，单元数据等效的系统试验时间为39.5 h，比最短的车长瞄准镜试验时间33.2 h要长些，因此取最短试验时间作为等效的系统试验时间方法也是不合理的，在一些可靠性试验中曾出现这种错误做法。

3)MTBF点估计值和单侧置信下限均有所提高，这是因为充分利用了单元试验数据，在系统试验信息之外又增加了额外信息，MTBF估计精度得到提高。

4)通过对单元试验信息的利用，可以提高等效后的总试验时间，因此可以适当减少系统试验时间，从而缩短试验周期和减少试验消耗。

4 结论

本文基于指数型串联系统模型，分别给出了定时截尾和定数截尾试验情况下的单元试验数据折算方法，依据折算方法可以充分利用单元试验数据，使得可靠性评估结果更反映武器装备的真实情况。得出主要结论如下：

1)利用只统计系统试验时间和统计所有故障数(单元和系统)的方案进行可靠性评估，是非常严苛的试验方法，试验结果偏于保守，也不够合理，在武器装备定型过程中容易引起生产方的争议。

2)丢弃单元试验数据的做法实际上损失了单元部分的可靠性试验信息，在单元试验时间比较长而系统试验时间比较短的情况下，可以考虑利用单元试验数据提高可靠性评估精度，减少试验消耗。

3)单元试验数据通过上文的折合算法可计算出等效的系统试验时间和故障数，可以合理利用单元试验信息，折合算法见(13)式、(14)式(定时截尾)或(19)式、(20)式(定数截尾)，两组公式是有区别的，定时截尾情况直接套用定数截尾的折合公式是值得商榷的。