随机组合约束下的联合火力打击弹药需求预测模型
2019-09-11薛辉王源张天鹏刘铁林
薛辉, 王源, 张天鹏, 刘铁林
(1.陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050003; 2.空军石家庄飞行学院, 河北 石家庄 050071; 3.国防大学 联合作战学院 联合参谋系, 河北 石家庄 050084)
0 引言
联合火力打击是以诸军兵种精确打击力量为主,在联合作战指挥机构统一指挥下,对敌重要目标进行的综合火力突击。由于联合火力打击涉及到的参战装备类型多,对参战装备的协同配合能力要求高,导致联合火力打击的弹药消耗呈现出很大的不确定性,因此种类合理、数量准确的弹药需求预测是确保联合火力打击作战效能的基本前提。如何科学、准确、合理地对联合火力打击弹药需求进行预测,提高弹药保障效能,进而增强武器装备作战效能,是当前高新技术条件下联合火力打击亟待解决的难题。
弹药需求预计的影响因素主要包括作战任务、作战样式、作战持续时间、对抗双方装备种类和数量以及敌方目标防护程度等[1]。目前常用的弹药需求预测方法有很多,主要包括弹药消耗标准修正法、经验推算法、理论计算法、基于人工智能的作战仿真法以及上述方法的融合,但对于联合火力打击背景下的弹药需求预测仍然缺乏行之有效的方法。弹药消耗标准修正法是以弹药消耗标准为基础,根据实际作战的具体条件进行合理修正,从而预计弹药需求量。弹药消耗标准是由XXX对作战部队规定进行一次或一日战斗任务的弹药消耗定额。该方法论证严密、科学合理且权威性强,是战时各级指挥员和机关制定作战方案、拟制弹药保障计划和组织弹药供应的基本依据。但随着武器装备及弹药性能的快速发展,尚无权威部门研究总结出联合火力打击弹药的消耗标准。经验推算法也称典型战例分析法,是通过对战例的分析研究来总结规律,并根据未来战争发展趋势和弹药特性进行必要的修正来预测弹药需求量。该方法简便易行,但只适用于传统战法下的弹药预测,而且难以从众多历史数据中选择出有一定相似程度的有效数据[2]。理论计算法主要根据敌我双方军事作战理论原则、武器装备编制数量、战术技术性能和战术手段等,用数学方法对弹药消耗数量进行计算,可以分为基于己方能力(LOE)和面向敌方目标威胁(TO)的弹药需求预测方法。基于LOE的研究有:文献[3-6]基于火力毁伤弹药需求理论,考虑武器系统毁歼概率、弹药毁伤机理,研究了敌方目标幅员和分布情况以及进攻策略的静态弹药消耗预测方法。基于TO的研究有:文献[7]利用加权平均的思想,提出了将不同目标的毁伤率综合计算的概念,体现了整体最优的思想,但不同目标之间的权重如何确定,尚缺乏合理有效的方法。文献[8]面向作战任务建立了高炮群的弹药消耗模型。借助人工智能辅助分析的仿真方法,主要以数学模型和Monte Carlo仿真技术为支撑,如文献[9]以对越自卫反击战中某型炮弹消耗量为仿真数据,将部分样本作为训练数据、部分样本作为预测验证数据,并引入遗忘因子,应用反向传播(BP)神经网络对炮弹消耗量进行了预测,但该方法对案例的依赖性较强,且缺乏确定性的数学模型基础。文献[10]对影响弹药用量的因素进行了分类,建立了评价矩阵及综合评价指标,并将其作为输入项训练神经网络,实现了对新战例弹药用量的预测。综上所述,基于能力[6,11]的弹药需求预测是以武器装备和弹药自身战术技术性能指标为依据,基于目标威胁[7,11]的弹药需求预测是以目标威胁的数量、程度和分布为依据,以上方法局限于武器- 弹药或者弹药- 目标二者之间的配置模式,而联合火力打击的对敌毁伤效果体现在武器- 弹药- 目标三者之间的最佳优化配置模式和目标分配原则。
因此,本文在借鉴上述方法基础上,根据联合火力打击的特点规律,首先,基于装备对抗的损失交换比建立装备- 目标的有效战斗力指数评估模型,以双方在交战过程中各自所发挥出来的实际作战能力作为目标分配原则,为弹药需求预测提供依据;其次,根据对敌最大毁伤原则,确立了以最大综合战斗力指数为目标函数的弹药需求预测模型;最后,考虑到弹药需求预测影响因素众多,如受指挥员作战意图、武器装备战术技术性能、作战条件以及保障能力等多种约束条件的随机组合影响,设计的数学模型可以灵活加入各种约束条件,以及设置各种约束条件之间的影响关系,运用智能优化算法求解模型,提高了预测速度及准确度。本文方法可为联合火力打击弹药需求的预测,以及作战方案和保障方案的制定、完善提供理论参考依据和方法支撑。
1 弹药需求预测模型的构建
联合火力打击注重的是火力协同配合,强调的是体系打击能力,追求的是整体毁伤效果。联合火力打击中同一类型武器平台可以打击多种目标,同一目标也可由多种武器平台进行打击,则联合火力打击弹药需求预测需要在火力分配的基础上进行,即由联合作战指挥机构统一分配最适宜的弹药,在最适宜的时机打击最适宜的目标。
进行火力分配的前提条件是制定目标分配准则及依据,本文按照装备- 目标的模式,确定不同目标对不同装备的战场价值,根据战场价值的高低确定弹药的分配方式及打击次序;基于武器装备对抗的损失交换比,互以对方装备为参考对象,按照敌方战场价值最优为原则,建立我方装备- 敌方目标的有效战斗力指数评估模型,以有效战斗力指数作为联合火力打击弹药需求预测的基本依据。
1.1 武器装备有效战斗力指数评估模型
假设我方拥有各类武器装备M种,第m种装备数量为cwm个,我方储备的弹药类型共有K种,敌方目标有N种,第n种目标数量分别为ctn个。我方武器装备和敌方目标用向量表示为
(1)
(2)
我方M种装备类型集合为W={W1,W2,…,Wm,…,WM},其标准战斗力指数为Pw={Pw1,Pw2,…,Pwm,…,PwM}。敌方N种目标类型集合为T={T1,T2,…,Tn,…,TN},其标准战斗力指数为Pt={Pt1,Pt2,…,Ptn,…,PtN}。由于不同装备打击不同目标会产生不同的对抗损失交换比,假设已知我方装备Wm与敌方目标Tn发生对抗时的损失交换比为Rm∶Rn. 针对对抗双方装备编成情况的不同,分别建立不同的有效战斗力指数计算模型,具体如下:
1)我方仅有一种装备,敌方仅有一种目标。如果双方仅有此两种装备发生对抗,则无论双方的战斗力指数取值为Pt(Rm/Rn)、Pt还是Pw、Pw(Rn/Rm),两种取值方式均可保持损失交换比不变。
2)我方仅有一种装备,敌方拥有N种目标。由于我方某种装备可以与敌方多种目标发生对抗,为便于通过对比,体现敌方不同目标之间战斗力指数的大小,并确定其对该装备威胁度的高低,本文规定选取我方装备的标准战斗力指数Pw作为参考对象,敌方目标对我方装备的损失交换比为{Rn/Rw},则敌方N种目标的有效战斗力指数为{Pw(Rn/Rw)}。
3)我方拥有M种装备,敌方仅拥有一种目标。我方多种装备均能与敌方目标发生对抗,在打击目标时存在协同配合问题,需要对我方装备的打击顺序进行排序。以敌方目标标准战斗力指数Pt为参考,我方装备对敌方目标的损失交换比为{Rm/Rt},则我方装备的有效战斗力指数为{Pt(Rm/Rt)}。
4)我方拥有M种装备,敌方拥有N种目标。双方均有多种装备时,无论是选取Pwm(Rn/Rm)还是选取Ptn(Rm/Rn),作为己方或敌方的有效战斗力指数,均会使同一装备存在多种战斗力指数,并会使损失交换比发生变化。考虑到确定有效战斗力指数的最终目的是评估敌方目标对我方装备威胁度的高低,因此首先以我方所有装备的标准战斗力指数为参考,对比所有Pwm(Rn/Rm),选取最大值max{Pwm(Rn/Rm)}作为敌方第n种目标的有效战斗力指数。如果最大值max{Pwm(Rn/Rm)}小于敌方目标的初始值Ptn,则仍取其原值,以确保敌方目标的有效战斗力指数不低于初始值。确定好敌方目标的有效战斗力指数后,根据损失交换比,可得我方装备打击敌方目标的有效战斗力指数,用矩阵表示如下:
(3)
式中:h=1,2,…,M,j=1,2,…,N;zwm,n表示我方第m种装备打击敌方第n种目标的有效战斗力指数。以此作为弹药需求预测的依据,不仅解决了目标威胁度量化评估难的问题,而且符合不同目标针对不同装备威胁度不同的作战规律。
根据装备对抗的损失交换比确定的有效战斗力指数,没有考虑不同装备打击目标所需的时间差异,假设不同装备打击不同目标的时间如下:
(4)
式中:twm,n表示我方第m种装备击毁敌方第n种目标所用的时间。在有效战斗力指数相同时,打击目标所用时间越短则作战能力越高。用装备的有效战斗力指数与其击毁目标所用时间的比值,来表示装备的作战能力,因此可以用swm,n=zwm,n/twm,n作为最终的有效战斗力指数,来表示不同装备对不同目标的作战能力。我方第m种装备打击敌方第n种目标的最终有效战斗力指数如下:
(5)
式中:swm,n表示我方第m种装备打击敌方第n种目标的最终有效战斗力指数。文献[12]为满足多类型武器协同火力优化打击的需求,建立了以对抗双方剩余价值比值为目标函数的协同火力打击决策优化模型,利用突击武器和打击目标的战场价值及相互之间毁伤概率建立了对抗双方剩余价值比值模型,其核心思想与本文有效战斗值指数评估模型是一致的,而且均是以比值方式对比不同武器的作战能力。
1.2 弹药需求预测目标函数的建立
由于联合火力打击是通过对敌整体毁伤效果达到最优来实现打击目的,即弹药需求的预测要符合对敌毁伤效果最优原则。为便于建模分析,做如下限定:
1)假设对抗双方的任一种武器至少可以受到敌方一种或多种武器的打击。因为如果任何一方拥有一种武器能够打击对方,而对方却没有合适武器进行还击,则该方有理由仅使用此种武器即可形成压倒性优势。在1.1节模型中将该类武器的有效战斗力指数设置为无穷大,在火力分配时将所有弹药都用于打击该目标,该情况不符合作战规律。
2)弹药需求预测仅考虑目标自身属性的直接价值,如打击人员时仅考虑杀伤人获得的战场收益,不考虑其丧失操作相应武器而带来的间接战场收益。
3)弹药消耗暂不考虑殉爆情况,即忽略由于敌方目标击中武器发射平台,导致未发射出去的弹药非正常消耗的情况。
4)联合火力打击过程中,如果对抗双方任一种装备被全部击毁,则需要根据1.1节方法重新进行有效战斗力指数评估。
联合火力打击弹药需求影响因素众多,且随着战场态势而不断变化,因此目标函数仅考虑对敌毁伤效果进行单一目标寻优。其他影响因素,如费用、时间、质量、体积、指挥员意图等可作为约束条件进行限制。具体计算过程如下:
步骤1已知我方不同种类的装备使用不同种类弹药,对敌方不同种类目标的命中概率将会不同,用(6)式表示我方第m种装备使用第k种弹药打击敌方第n种目标的命中概率:
(6)
式中:i=1,2,…,K;Pm,k,n表示我方第m种装备使用第k种弹药打击敌方第n种目标时的命中概率。
目标被弹药命中后不一定丧失全部作战功能,且不同弹药对不同目标的毁伤效果差异也很大,用毁伤概率表示为
(7)
式中:ωm,k,n表示我方第m种装备使用第k种弹药击中敌方第n种目标时的毁伤概率。
根据以上武器装备的战术技术指标,可按(8)式、(9)式求出毁伤目标所需的平均有效射弹发数。假设某型武器装备对某型目标的单发命中概率为P,单发目标毁伤概率为ω,则所需的平均有效射弹发数为
(8)
(9)
通过(6)式、(7)式、(9)式计算后,可得我方第m种装备使用第k种子弹击毁敌方第n种目标所需的平均射弹发数,令
(10)

步骤2联合火力打击对敌的毁伤效果不仅取决于充足的弹药,还涉及到己方装备和敌方目标情况,即:一要己方拥有可用的装备;二要敌方拥有可打击的目标。因此将己方装备和敌方目标的打击情况设置如下:
假设Owpm为我方第m种装备的分配情况:
(11)

(12)
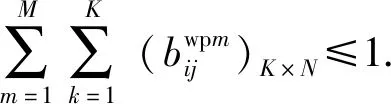
步骤3对抗双方的装备、目标向量以及有效战斗力指数矩阵作如下变换。
令变换后的装备矩阵为
(13)
式中:
cwm,k,n=cwm.
(14)
令变换后的目标矩阵为
(15)
式中:
ctm,k,n=ctn.
(16)
令变换后我方第m种装备的标准战斗力指数为
(17)
式中:
swm,k,n=swm,n.
(18)
步骤4弹药消耗情况与装备- 目标的分配情况有关,随着装备- 目标分配情况的变化而变化,对应的弹药消耗情况为
(19)
(20)
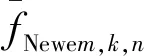
以上弹药消耗情况仅考虑了装备- 弹药- 目标的最优配置,但联合火力打击弹药的实际使用情况还往往受到很多其他因素的影响和制约,为便于设置各种约束条件,作如下设计,我方第m种装备的弹药规划情况如下所示:
(21)
式中:fwpm,k,n为规划的第m种装备使用第k种弹药打击第n种目标时每个装备的平均需求发数。
令SNewwm为我方第m种装备根据火力分配结果实际发挥出来的战斗活力,我方第m种装备打击敌方目标的综合战斗力指数为
(22)
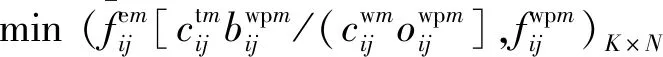
步骤5定义我方所有武器装备在对抗过程中,通过有效毁伤敌方目标而发挥出来的战斗活力之和,称为综合战斗力指数。在满足各种弹药需求预测约束条件前提下,cwm个第m种装备发挥出来的有效战斗力指数为
(23)
则我方所有装备的综合战斗力指数为
(24)
显然,S∑Neww越高,对敌毁伤效果越好,S∑Neww最大时则达到对敌最佳毁伤效果。此时第m种装备消耗的第k种弹药数量为
(25)
我方所有装备消耗的第k种弹药数量为
(26)
2 弹药需求预测约束条件设置
联合火力打击弹药的需求预测除了考虑弹药对目标的毁伤特性、我方装备情况、敌方目标情况,约束弹药需求的因素往往还有很多。
2.1 弹药发射能力约束
弹药发射数量受到发射平台发射速度、发射平台技术可靠性以及作战环境等因素的影响,每一种武器装备并不能完全按最大射速发射,需要结合实际进行调整。根据以往的实际战例统计,假设在规定或假设的战斗时间间隔内我方装备的弹药最大发射发数为已知,可表示为
(27)
式中:fm,k为我方第m种装备在一定的战斗时间间隔内能够发射第k种弹药的最大数量。显然,用来打击所有目标的第m种装备的第k种弹药总数要小于其最大发射发数:
(28)
2.2 弹药体积、质量的约束
战时受作战环境、地形地貌限制,装备保障部门的携运行能力具有很大差异,因此弹药需求预测受到其体积和质量的约束。
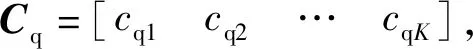
(29)
2.3 弹药准备时间的限制
随着弹药智能化程度的不断提高,其发射前的准备时间也越来越长,有的智能弹药甚至还需使用专用的检测设备进行测试后才能正常使用。因此预测弹药需求量时还应考虑弹药准备时间的限制。
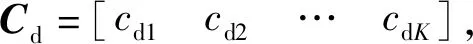
(30)
2.4 指挥员作战意图的限制
战争作为复杂巨系统,战术层次的最优不一定会达到战略层次上的最优。按照武器战术性能指标去规划弹药可以达到战术层次的最优解,但不一定是战略层次的最优解。例如有些目标的重要性或威胁度并不总能从其战术技术特性反映出来,如敌方的运输设备或保障装备,其威胁度及战场价值并不能直接体现,而是通过保障其他作战装备间接实现;如某个指挥所并不具备直接打击能力,但其调度指挥火力的能力使其战场重要度反而很高。因此军事指挥员有时会根据作战意图指定某武器使用某种弹药打击某种目标,则该类弹药的消耗量需要在预测时做出特殊限制。可以采用固定比例或区间的限制方法,如可以指定某种装备对某种目标进行打击时所使用弹药的比例,αwm,k,n为军事指挥员指定的我方第m种装备使用第k种弹药打击敌方第n种目标的情况,未指定的为0:
(31)
规划的弹药发数不应少于指挥员规定的发数,则令
(32)
(32)式可保证第m种装备使用第k种弹药打击第n种目标时所规划的发数不小于军事指挥员规定的数量。
2.5 装备使用优先级的限制
遂行联合火力打击任务的装备不仅需要按照其设计特性打击最适宜的目标,还应根据作战实际适时地打击目标,实现真正意义的联合火力打击,文献[13]基于随机时间网络研究了联合火力打击方案优化问题,突出强调了作战时机对联合火力打击效果的影响。不同时机时敏目标必须在有限的攻击窗口或交战机会内发现、定位、识别、瞄准和攻击,因此当存在多种装备可以打击该目标时,必须设置一定的打击规则,使装备依据各自的优先级有序打击目标,以便准备把握战机,如某航空导弹,在其飞行中段时的速度及轨迹较为稳定、可预测强,便于进行拦截与打击,必须抓住该时机进行有效打击。因此,装备的使用优先级对联合火力打击弹药需求的约束影响如下:
假设敌方N种目标的攻击时间窗口为
(33)
打击不同目标时我方装备从准备、瞄准到击发,完成一次射击动作所需的时间也是不同的,我方装备完成一次发射所需时间如下:
(34)
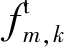
弹药发射后到完成击毁目标并非一瞬完成的,会受到多种因素的制约,如弹药飞临时间、敌方反导武器拦截、做出战术规避等,所以也会消耗一定时间,我方弹药发射后至击毁敌方目标所需时间如下:
(35)
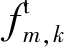
3 算例分析
3.1 参数假设
为了验证模型的可行性和有效性,做出如下参数设置,我方装备及敌方目标编成如表1所示,我方装备对敌方目标的有效战斗力指数如表2所示。
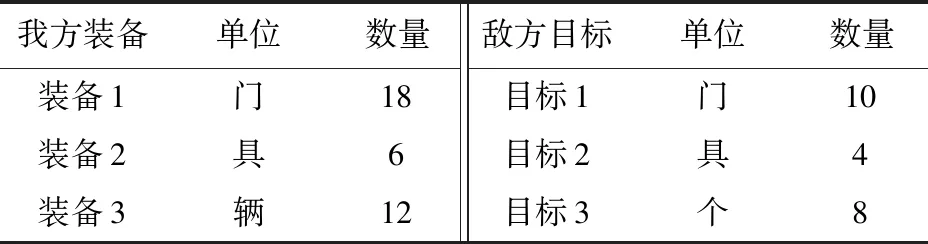
表1 我方装备及敌方目标编成
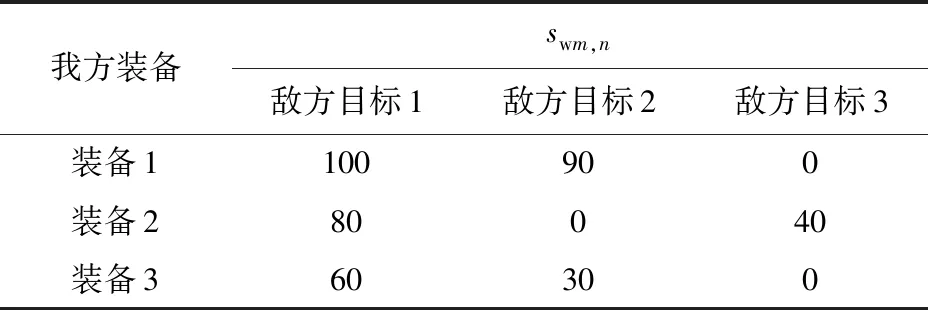
表2 我方装备的有效战斗力指数swm,n
根据武器装备使用不同弹药对不同目标的命中概率和毁伤概率,不同装备使用不同弹药击毁不同目标的平均有效射弹发数如表3所示,最大发射发数如表4所示。
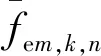
表3 我方装备平均有效射弹发数

表4 我方装备在此次战斗中最大发射发数fm,k
3.2 模型求解
由于弹药需求预测影响因素众多,且数据规模庞大,复杂度是指数级的,其计算时间往往太长,采用现代的智能进化算法是当前解决非确定多项式NP难问题的主要方法之一,本文为快速求解模型,采用遗传算法工具箱,设置如下:function [x,fval,exitflag,output,population,score]=DYGH_GA(nvars,Aineq,bineq,Aeq,beq,LB,UB)。nvars为变量个数,由于本文案例是按照装备- 弹药- 目标优化编组模式下的三维弹药需求预测框架,变量个数为3×N×M×K个,随着约束条件的增多,其变量个数为N×M×K整数倍的增长。Aineq为(M+N+MK)×3×N×M×K阶的矩阵,bineq为M+N+M×K阶的列向量,LB、UB分别为约束条件的上限、下限。设置遗传算法的种群规模为200、进化代数为100以及相应的终止条件。
3.3 结果分析

图1 遗传算法寻优过程示意图Fig.1 Schematic diagram of genetic algorithm optimization process
目标函数的寻优过程如图1所示。弹药需求的预测结果向上取整后,如表5所示。
此时,对敌方目标的最大综合战斗力指数为1 150.22,该弹药需求预测结果达到了对敌联合火力打击的最佳毁伤效果。与文献[14]基于毁伤能力匹配的单目标、单弹种的弹药需求预测核心思想一致,并且进一步实现了联合作战条件下多目标多种类弹药的需求预测。文献[15]提到的基于武器- 弹药- 目标编组的弹药消耗模型方法,指出编组的优化配置主要依赖于军事专家的经验,缺乏科学的定量分析方法。本文最大综合战斗力指数法有效解决了该问题,实现了对敌最佳毁伤效果前提下的弹药需求预测,同时也是装备- 弹药- 目标的最优编组模式。
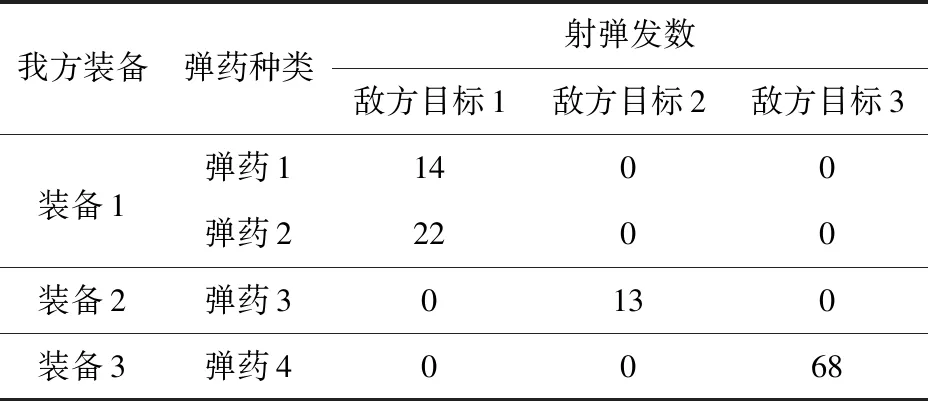
表5 联合火力打击弹药需求预测结果
4 结论
本文以基于对抗损失交换比的武器装备有效战斗力指数评估结果为联合火力打击弹药需求预测依据,按照对敌最大毁伤原则,以最大综合战斗力指数为目标函数,建立了装备- 弹药- 目标最优编组模式下的弹药需求预测模型。该模型具有很强的可操作性,符合作战领域“木桶效应”的实际。所得主要结论如下:
1)基于武器装备对抗损失交换比建立的装备- 目标有效战斗力指数评估模型,将装备的标准战斗力指数转化为对抗过程中实际发挥出来的有效战斗力指数,使得联合火力打击弹药需求预测结果更加符合作战实际。
2)以最大综合战斗力指数为目标函数建立的弹药需求预测模型,体现了武器装备、发射弹种和攻击目标之间的多对多对应关系,以及三者之间的协同效果和相互制约关系,算例结果表明该方法可有效提高联合火力打击的协同效应,促进装备保障方案与作战计划的协调统一。
3)结合战场态势及作战意图随机组合弹药需求预测约束条件的设计理念,使得弹药需求预测更加符合军事需求。
综上所述,本文方法预测的弹药需求可以显著提高武器装备作战效能,增强打赢能力,以及对于预前开展各项装备保障工作具有很强的指导作用。
