事件驱动多关节机械臂轨迹跟踪自适应鲁棒控制
2019-09-11钱前张爱华孙艺瑕
钱前, 张爱华, 孙艺瑕
(上海工程技术大学 机械与汽车工程学院, 上海 201600)
0 引言
多关节机械臂控制系统是具有强耦合性和复杂非线性的系统,可以克服不确定干扰和建模误差的影响是设计控制器要考虑的首要问题,因此非线性鲁棒控制算法得到了广泛应用。文献[1]将负载质量从机器人动力学方程中分离出来,针对负载未知时在广义坐标空间和任务坐标空间中的轨迹跟踪控制问题,研究了扰动有界时的鲁棒自适应控制。文献[2]针对系统中存在有界未知负载等非线性不确定项的影响,通过状态方程匹配将鲁棒控制问题转换为最优控制问题进行求解,得到了控制算法,并验证了控制器的有效性。以上两种鲁棒控制针对的机械臂控制系统形式要求比较严格,解算过程比较耗时。文献[3]通过合理选择与控制目标相关的势函数,根据模型中不确定性的实时变化,通过引入可在线可调参数得到自适应鲁棒控制算法,保证了闭环系统中所有状态半全局最终一致有界。文献[4]针对直流电机驱动的机器人系统,通过Takagi-Sugeno(T-S)模糊模型处理不确定性,设计神经网络鲁棒自适应控制器,节约在线计算量,有利于实时控制。以上控制算法都是基于采样周期的时间驱动控制系统,而随着信息技术和经济的发展,除了对机械臂控制系统稳定性和鲁棒性的要求以外,系统能耗和对通信频率的要求必须考虑。文献[5-6]初步研究了降低系统能耗的控制方法,但仍通过传感器与控制器的周期性采样执行,虽然减少了机器人控制系统的通信频率,但这些算法可能需要较高的采样频率,为此事件驱动控制方法引起了国内外专家学者们的注意。
事件驱动控制系统的控制指令只有满足驱动条件时才会更新,控制器的执行不再具有周期性,是与系统状态相关的。文献[7-8]提出一种连续时间控制与事件驱动控制相结合的方法,解决了2阶非线性系统轨迹跟踪的问题;文献[9]采用连续比例- 积分- 微分(PID)控制与事件驱动控制相结合方法解决了机器人轨迹跟踪问题,但提出算法是基于精确模型的;文献[10]将状态反馈应用到事件驱动控制,但不能完全补偿模型的不确定性;文献[11]将神经网络滑模控制应用到机器人事件驱动控制,有效地补偿了模型不确定性,但缺少自适应;文献[12]提出一种基于事件驱动的轨迹跟踪自适应算法,解决了当机器人控制系统动力学未知时的轨迹跟踪问题;文献[13]将文献[12]的算法应用到全驱动水面船轨迹跟踪系统,但未考虑到外界干扰;文献[14]提出一种基于滑模控制的事件驱动控制方法,解决了带有外部扰动的线性系统中能耗较高问题;文献[15]针对带有外部扰动的非线性系统能耗较高问题,提出了一种事件驱动滑模控制算法;文献[16]将此算法应用到带有外部扰动的欧拉- 拉格朗日轨迹跟踪系统中,但滑模控制是不连续的,系统的稳定性需要牺牲切换面的带宽。
鉴于自适应鲁棒控制处理非线性系统稳定性和鲁棒性问题的良好表现,本文针对带有不确定干扰和建模误差的多关节机械臂跟踪控制系统,提出事件驱动自适应鲁棒轨迹跟踪控制器,来解决高精度多关节机械臂跟踪系统在跟踪过程中高能耗、通信频率要求较高的问题,设计鲁棒控制算法补偿不确定干扰和未知模型动态干扰,自适应地调节系统参数,并通过Lyapunov稳定性理论获得驱动条件,保证系统的稳定性以及系统中无Zeno现象发生,最后通过仿真验证控制器的有效性。
1 问题描述
考虑外界扰动和建模误差的影响,建立多关节机械臂跟踪控制系统数学模型[17]如下:

(1)

多关节机械臂轨迹的跟踪控制目标如下:

(2)
式中:e为系统位置跟踪误差;qd为给定的期望轨迹。
由于外界干扰通常是有界的,对于多关节机械臂跟踪控制系统,本文做出如下合理假设:
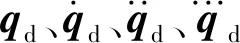
定义系统位置跟踪误差为
e=q-qd,
(3)
并令

(4)
为多关节机械臂轨迹跟踪误差系统,其中u表示控制器的输出,从而可以将数学模型(1)式改写成如下系统模型:
(5)
2 事件驱动鲁棒自适应跟踪控制
2.1 自适应鲁棒控制器
定义θ(t)=[θ1(t)θ2(t)]T为可调自适应参数,设计多关节机械臂跟踪控制器:
(6)
并选择如下自适应律:
(7)


紧集Ω0为
(8)
紧集Ωe为
(9)
式中:η1、η2、t0、T为正常数。
为了方便证明,本文给出如下引理:
引理1[18]令Ω为任意的闭凸集,则有(v-PΩ(v))T(PΩ(v)-w)≥0,v∈Rl,w∈Ω,其中PΩ(v)为Rl→Ω上的投影算子,v、w为实矩阵,l为维度。
证明定义∈R2为常值向量,选择Lyapunov候选函数:
(10)
式中:V0、V1分别为
(11)
(12)

(13)

(14)
式中:
(15)
对(10)式中的V1(θ(t))求微分,可得

(16)
式中:
r(θ)=ψ(θ-β1F(θ))-θ.
(17)
令v=θ-β1F(θ),w=,根据引理1,有
(r(θ)+θ-)T(-r(θ)-β1F(θ))≥0.
(18)
整理(18)式,可得
(19)
将(19)式代入(16)式,得
(20)
由于
(21)
将(4)式代入(21)式,有
(22)
对(22)式取反馈控制律u,有
(23)
将(23)式代入(22)式,有
(24)
进而得到
(25)
针对(15)式给出的c(θ1(t),v),定义如下定理:


(26)
式中:λ1、λ2分别为
(27)

c(θ1(t),v)≤0,t≥t0+T.
(28)

(29)
通过适当选择设计参数η1、η2,可使系统达到规定跟踪精度;又根据假设2,参考信号qd有界,则闭环系统状态q必定有界。证毕。
2.2 事件驱动鲁棒自适应控制器
定义控制力矩τ为
τ=τ(η),
(30)

定义ti{i=0,1,2,…}为由驱动状态决定的事件驱动控制器的时间序列,则事件驱动控制力矩为
τ=τ(η(ti)).
(31)
鲁棒自适应控制器与事件驱动控制器的测量误差为
(32)
式中:
(33)
针对事件驱动多关节机械臂控制系统给出如下假设:


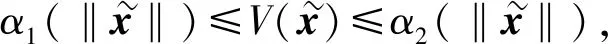
(34)

根据(32)式、(33)式,可得事件驱动控制器:
(35)
将(35)式代入(22)式,有
(36)

(37)
于是,对于∀γ∈Ω1, ∀η1,η2∈Ωe,有
(38)
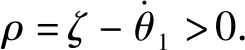
(39)

进而对于t∈[ti,ti+1)得到时间驱动控制器为

(40)
(41)
将(30)式代入(41)式,可得
(42)
根据(37)式与定理1可得
(43)
式中:P1=‖sup (-θ1(M-1)T-C)‖;P2=‖max {M-1P1,1}‖;P3=max {P2,1,L}.
(44)
根据(43)式、(44)式与假设3,可得
(45)

(46)
考虑(40)式与(46)式可知T0存在,并且形式为
(47)
根据(47)式可知T0的下界大于0,因此该系统中没有Zeno现象发生。
3 仿真分析
本文使用文献[20]中给出的3关节机械臂作为仿真对象,机械臂结构与相关参数如图1所示,相关参数如表1所示。图1中:I1、I2、I3分别为关节1、关节2、关节3的转动惯量,l2、l3分别为关节2、关节3连杆长度,m2、m3分别为关节2、关节3连杆质量,r2、r3分别为关节2、关节3连杆质心到转动关节的距离,q1、q2、q3分别为关节1、关节2、关节3的位置。

图1 3关节机械臂结构图Fig.1 Three-links multi-joint manipulator

参数数值参数数值参数数值I1/(kg·m2)3.61l2/m1r2/m0.6I2/(kg·m2)2.35m2/kg30r3/m0.5I3/(kg·m2)1.95m3/kg26g/(m·s-2)9.8
注:g为重力加速度。
惯性矩阵M(q)为
M(q)中各个元素具体表达式如下:
m11=I1+a1cos2q2+a2cos2(q2+q3)+
2a3cosq2cos (q2+q3),
m22=I2+a1+a2+2a3cosq3,
m33=I3+a2,m32=m23=a2+a3cosq3,

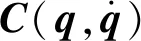



系统初始状态为
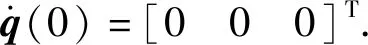
摩擦力为
其中μ1=5 N·m,μ2=5 N·m,μ3=5 N·m.
外部干扰为d1=0.1sint,d2=0.1cos (0.5t),d3=0.1sin (t/3),鲁棒自适应参数为β1=5,β2=5,β3=2,α=2,事件驱动控制参数为σ=0.8,ε=0.5.
设定仿真时间100 s,仿真步长为0.01 s,仿真结果如图2~图5所示。

图2 机械臂3个关节的跟踪效果图Fig.2 Tracking results of three joints

图3 机械臂3个关节跟踪误差变化Fig.3 Tracking errors of three joints

图4 机械臂3个关节控制力矩变化Fig.4 Control torques of three joints

图5 控制器触发情况图Fig.5 Change of inter-update time of controller
为验证本文所提出的事件驱动自适应鲁棒控制方法的有效性与控制效果,仿真时与无事件驱动的自适应鲁棒跟踪控制方法进行对比,即与参数σ=0,ε=0的仿真结果进行对比。图2为事件驱动自适应鲁棒控制与无事件驱动的轨迹跟踪效果对比图,图3为两种控制方法的跟踪误差变化曲线。从图2和图3可看出:两种方法都能够完成轨迹跟踪,无事件驱动时跟踪效果较好、跟踪精度高,说明所提出的自适应鲁棒控制跟踪效果良好,且对干扰变化不敏感;事件驱动的控制方法也能够较好地完成跟踪控制,但因其无需频繁的发送控制指令驱动执行机构,而使得其控制效果稍逊于无事件驱动跟踪控制,控制力矩指令如图4所示。
图4为有无事件驱动两种情况下机械臂3个关节的控制力矩指令变化图。从图4中可看出:系统在有事件驱动策略时的关节1力矩在0~20 s的变化浮动相比无事件驱动策略时更接近0;关节2与关节3的力矩在有事件驱动策略时变化相对更加平稳,可以在保证控制效果的情况下有效减少能量损耗。图5为有无事件驱动策略时控制触发时间间隔变化图,从中可看出有事件驱动策略时的驱动间隔大于0且明显大于无事件驱动策略的驱动间隔,即无Zeno现象发生。对应图4可以看出,系统在触发间隔内控制力矩保持不变,说明了事件驱动控制的执行不再具有周期性,可以有效降低系统的通信频率。
4 结论
为解决存在不确定干扰和建模误差的多关节机械臂轨迹跟踪问题,本文提出了一种事件驱动自适应鲁棒控制器。根据Lyapunov稳定性理论设计了驱动条件,证明了无Zeno现象,并通过一个典型3关节机械臂进行了仿真验证。仿真结果可以看出,所提出的自适应鲁棒控制具有良好的跟踪效果,有效解决了系统高能耗和通信频率较大的问题。具体结论为:1)该控制器可以通过自适应策略调节参数,从而保证系统轨迹跟踪精度,所提出的控制算法保证了事件驱动多关节机械臂跟踪控制系统状态半全局最终一致有界;2)结合事件驱动策略所得到的事件驱动控制系统在保证跟踪效果的同时,有效降低了系统通信频率,减少能源消耗,系统不存在Zeno现象;3)仿真中发现驱动参数σ和ε越大,需要的通信频率就越低,指令更新频率越低,但是过低的指令更新频率会导致大的跟踪误差,从而导致频繁地触发驱动函数,为此设计控制算法来完成驱动参数的自适应调节是下一步的研究工作。
