基于半监督聚类的网络嵌入方法
2019-09-10张静李文斌张志敏
张静 李文斌 张志敏




摘要:GEMSEC(graph embedding with self clustering)在计算节点特征的同时学习节点聚类,通过强制将节点进行聚类来揭露网络中的社区结构,但未考虑类别标签信息,导致学到的节点嵌入缺乏区分性。针对这一问题,提出了一种基于半监督聚类的网络嵌入方法(NESSC),将随机游走序列和少量节点类别标签作为输入,在计算节点特征和学习节点k-means聚类的过程中,利用类别标签信息指导聚类过程,同时重构已知节点类别标签信息,学习具有区分性的节点表示。在6个真实网络上进行节点聚类和节点分类评测实验,实验结果显示,NESSC方法明显优于无监督网络嵌入方法DeepWalk和GEMSEC,可以通过加入节点的标签信息来提高网络嵌入的效果。因此,通过网络节点的嵌入,可以高效地提取网络的有用信息,对于相关网络嵌入研究具有一定的参考价值。
关键词:人工智能其他学科;网络嵌入;聚类;半监督;区分性
中图分类号:TP181文献标志码:Adoi: 10.7535/hbgykj.2019yx04004
Abstract:GEMSEC(craph embedding with self clustering) learns a clustering of the nodes simultaneously with computing their features, and reveals the natural community structure in the network by enforcing nodes to be clustered. However, it fails to consider label information, which leads to the lack of discrimination of learned node embedding. To solve this problem, a network embedding method based on semi-supervised clustering(NESSC) is proposed, which takes the random walk sequence and a small amount labels of nodes as input, and the label information is used to guide the clustering process in the process of learning node features and node clustering learning, and the known node label information is reconstructed to learn the discriminative node representation. Finally, an experimental evaluation of node classification is performed, using six real-world datasets. The results demonstrate that NESSC is obviously superior to unsupervised network embedding methods DeepWalk and GEMSEC, which indicates that the effect of network embedding can be improved by adding the label information of nodes. This method can extract useful internet information effectively by embedding of network nodes, which provides reference for the study of network embedding methods.
Keywords:other disciplines of artificial intelligence; network embedding; clustering; semi-supervised; discrimination
現实世界中的复杂系统通常都可以建模为网络,如社交网络、生物网络、引文网络等,其中数据样本对应于网络的节点,数据样本之间的关联对应于网络的边。对这些网络的分析在许多新兴应用中发挥着重要的作用[1],如在社交网络中,将用户划分为有意义的社交群体对于用户搜索、定向广告和推荐等许多重要任务都是有用的;在生物网络中,推断蛋白质之间的相互作用可以促进形成疾病治疗的新方法。但由于高维度和数据稀疏等问题,使得传统的基于邻接矩阵的网络表示形式很难在大数据环境下推广。因此,寻找网络节点的有效低维向量表示,高效提取网络的有用信息,具有重要的学术意义和广泛的应用价值[2]。
网络嵌入[3-5]通过保留网络拓扑结构等信息,将复杂网络中的节点嵌入到低维、连续的向量空间,使得具有相似结构的节点在向量空间中有相近的向量表示。网络嵌入通过优化算法自动得到网络节点表示,可以有效降低复杂度,方便进行分布式并行计算,同时还可以直接应用前沿的机器学习算法对网络数据进行高效分析与处理。
1相关工作
传统的网络嵌入方法是基于矩阵特征向量计算的,例如,局部线性表示(locally linear embedding,LLE)[6]和拉普拉斯特征映射(Laplacian eigenmaps,LE)[7]。该类方法依赖于关联矩阵的定义和构建,需要对关联矩阵进行特征值计算,时间、空间复杂度较高,不适用于大规模网络的嵌入学习。
近年来,基于神经网络的网络嵌入技术逐渐引起学术界的关注。受神经网络语言模型Word2vec[8]的启发,PEROZZI等[9]提出了DeepWalk方法,将在复杂网络中随机游走得到的节点序列看作是文本中的句子,将序列中的节点看作是文本中的单词,通过Skip-Gram模型得到网络节点嵌入表示。由于随机游走序列只依赖于局部信息,使得DeepWalk模型计算时间、空间消耗較小。之后,Node2vec[10]对DeepWalk的随机游走策略做出了改进,引入深度优先搜索和宽度优先搜索来捕获节点的结构对等性和同质性特点,因此可以得到更高质量的嵌入表示。LINE[11]通过对网络节点的一阶相似性和二阶相似性建模优化,来捕获网络的一阶和二阶邻近特征。为了获取节点的高阶特征表示,GraRep[12]在LINE基础上进行更高阶相似性关系的建模。
保持网络结构是网络嵌入的基本要求,以上方法只考虑网络的局部结构,如节点的一阶和二阶相似性,忽略了全局结构。MNMF[13]将社区结构纳入到网络嵌入中,然后在统一的框架中共同优化基于NMF的嵌入表示学习模型和基于模块的社区检测模型,从而使学到的节点表示能够同时保持网络的微观结构和社区结构。但该方法是基于矩阵分解的,复杂度较高,不能处理大规模网络。GEMSEC[14]将聚类约束引入节点嵌入优化目标,在学习节点特征的同时,对节点进行k-means聚类,用聚类的结果来影响节点嵌入的学习,使得到的节点嵌入表示能够保持网络的潜在聚类结构。同时,由于该方法是基于序列的网络嵌入模型,运行时间复杂度在节点数上是线性的。但以上网络嵌入方法都是无监督的,学到的特征缺少区分性,导致在某些特定任务上效果不好。
网络中除了网络拓扑结构信息,还有着丰富的伴随信息,如节点的类别标签信息。引入节点的类别标签信息可以增强学到嵌入表示的区分性。CHEN等[15]提出一种融合群内部结构和跨群信息的网络嵌入训练模型GENE, 通过在游走序列中添加包含节点标签信息的标签节点, 实现网络结构信息与标签信息的融合。TU等[16]提出基于最大间隔的DeepWalk模型MMDW(max-margin DeepWalk),将节点的类别标签信息融入到节点嵌入向量中,学习有区分性的节点嵌入表示。
本文从融合网络结构与节点标签类别信息出发,提出了一种基于半监督聚类的网络嵌入方法NESSC,该方法首先受GEMSEC的启发,在计算节点嵌入特征的同时对节点进行k-means聚类,使学到的节点嵌入能更好地保持网络的潜在聚类结构,但在聚类的过程中加入了类别标签信息,利用少量已知节点的类别标签指导节点聚类过程;其次,为了更加充分地利用已知节点的类别标签信息,将最小化已知节点所属类别损失加入到节点嵌入优化的目标中,学习最优化的嵌入表示。
2基于半监督聚类的网络嵌入方法
2.1定义
为更好地描述所提出的模型及其具体算法,首先给出以下相关符号及其含义,如表1所示。
定义1网络嵌入:又称网络表示学习,给定一个网络G=(V,E),通过学习一个映射函数f: v→f(v)∈Rd,将网络结构嵌入到低维向量空间,其中d|V|。映射函数f保留了网络G的结构信息,使得具有相似结构的节点具有相近的向量表示。
定义2半监督网络嵌入:给定一个含有少量节点类别标签L的网络G=(V,E,L),通过整合给定少量节点标签与网络拓扑结构来学习网络节点的嵌入表示。
2.2模型描述
笔者提出的基于半监督聚类的网络嵌入方法NESSC,以DeepWalk模型为基础,最大化观察源节点与其上下文邻居节点共现的概率,保留网络的邻近结构特征;其次,添加k-means聚类损失强制节点嵌入表示进行聚类,同时利用已知节点的类别标签对节点聚类过程进行指导,保持网络的全局潜在聚类结构;最后,添加重构已知节点类别标签信息损失,联合训练优化,学习具有辨别性的嵌入表示。
首先基于顶点个数、类别个数和嵌入维度初始化模型参数。之后,进行N次迭代,每次迭代中,先对节点集进行重新洗牌,再逐点遍历打乱后的节点集,采样节点序列,并根据窗口w提取邻居节点集合,更新聚类平衡参数和学习率,最后使用随机梯度Adam算法更新节点和类中心的嵌入向量。在针对每个节点的计算过程中,采用负采样来降低复杂度,计算次数从|V|次减少为m次。遍历整个节点集合,计算次数为(1+m+k)·w·len,迭代N次,整体计算复杂度为O((1+m+k)·w·len·|V|·N)。由于m,k,w,len,N|V|,所以NESSC方法时间复杂度为O(|V|),可以应用于大规模网络嵌入学习任务中。
3实验结果分析
为了充分说明NESSC方法的有效性,在真实数据集Citeseer,Cora及WebKB上进行节点聚类和节点分类2个任务,并将得到的结果与DeepWalk,GEMSEC算法进行比较。
3.1实验设定
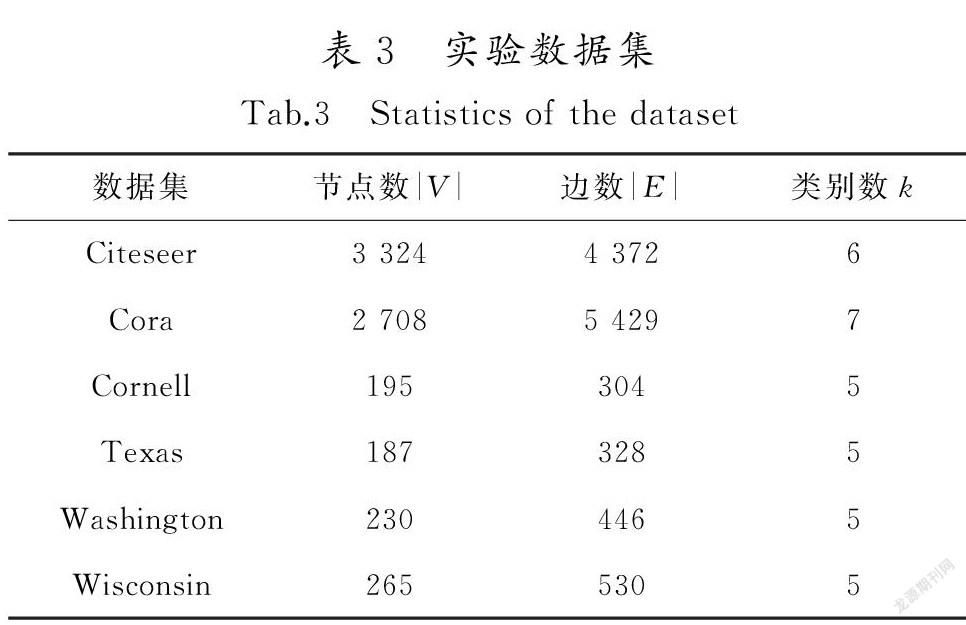
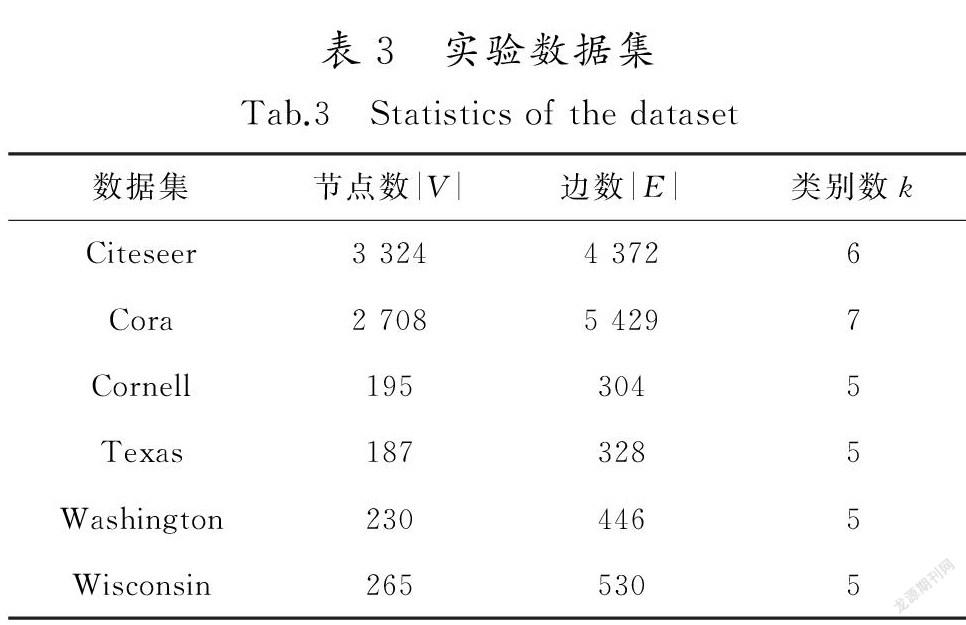
3.1.1数据集
在数据集Citeseer,Cora及WebKB进行评测任务,其中WebKB包括Cornell,Texas,Washington和Wisconsin等4个子数据集。各个数据集去掉孤立点之后,统计信息如表3所示。
3.1.2实验环境及参数设定
实验硬件环境采用联想台式机,操作系统为Windows7,处理器为 Intel Core i7-3770,内存为 8 GB,硬盘为500 GB,软件环境采用 Python3.6。
考虑算法比较的公平性,共同参数设置为嵌入维度d=64,负采样个数m=5,窗口大小w=5,初始学习率ηinit=0.01,最小学习率ηmin=0.001。为了取得最优的节点嵌入向量,针对各数据集的参数设定如表4所示。针对半监督的网络嵌入方法NESSC,设置已知类别标签节点的比例为0.05, 01, 0.15, 0.2, 0.25, 0.3,选取方式为随机选取。
3.2聚类结果及分析
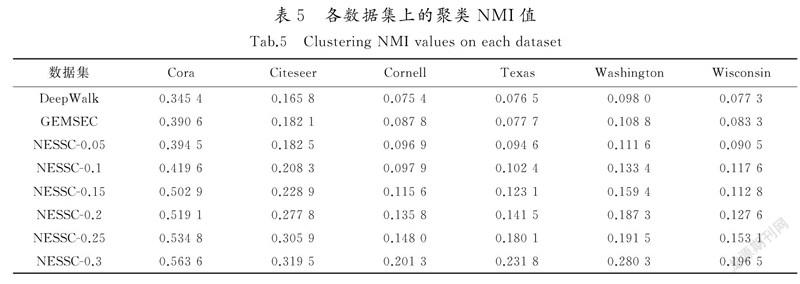
将NESSC学到的嵌入向量用于节点的聚类任务,以此来评估学到嵌入向量的质量。本实验采用k-means聚类,采用标准互信息NMI[18]评估,进行独立重复实验10次,取其平均值作为最终结果。表5记录了无监督方法DeepWalk,GEMSEC和半监督方法NESSC在Citeseer,Cora及WebKB数据集上的聚类NMI值,其中NESSC-0.05表示采用NESSC方法對已知类别标签节点为5%的数据集进行实验,以此类推。
从表5聚类结果可以看出:1)GEMSEC效果优于DeepWalk,在Citeseer数据集上表现更为明显,NMI值提高4.52%,这说明了强制节点嵌入表示进行聚类,可以揭示网络社区结构,使学到的节点嵌入表示保持网络的潜在聚类结构;2)NESSC处理效果明显优于GEMSEC和DeepWalk,这是因为GEMSEC和DeepWalk属于无监督的算法,虽然计算简单,但准确率低。而NESSC充分利用已知节点的标签信息实现半监督的嵌入表示,因此性能更优,而且随着已知类别标签节点的增加,得到的效果更好。在实际应用中,可以通过加入少量节点标签信息的代价来获得网络嵌入算法性能的较大提升。
3.3分类结果及分析
首先利用NESSC方法得到节点的嵌入表示,然后作为节点分类任务的输入,用分类任务的效果来评价学到嵌入表示的质量。分类采用KNN[19],评估方法采用准确率Accuracy,数据集分割方法采用10折交叉验证[19],同时为了减弱随机性,独立重复进行10次实验,取其平均值作为最终结果。表6记录了无监督方法DeepWalk,GEMSEC和半监督方法NESSC在Citeseer,Cora及WebKB数据集上的分类准确率值。
由表6可以看出:1)在数据集Cora,Citeseer,Texas和Wisconsin上,GEMSEC效果略优于DeepWalk,这表明在计算节点嵌入特征的过程中强制节点嵌入表示进行k-means聚类,学习网络的社区结构,对节点嵌入向量的学习产生一定的积极影响;2)NESSC处理效果明显优于GEMSEC和DeepWalk,而且随着已知类别标签节点的增加,得到的效果更好,这在数据集Texas和Washington上表现尤为明显。这表明少量节点类别标签信息的加入可以明显提升节点嵌入表示的质量。NESSC充分利用少量节点的类别标签信息实现半监督的网络嵌入,学习具有区分性的嵌入表示,性能更优,但仍然存在一定的错误率,这是因为NESSC属于半监督模型,加入已知标签的节点较少,但随着已知标签节点的比例增大,NESSC会取得更好的结果。
3.4参数敏感性分析
基于半监督聚类的网络嵌入方法NESSC含有2个主要参数:聚类损失平衡参数γ和重构已知节点类别标签信息平衡参数β。选择数据集Citeseer和Cornell,已知类别标签节点的比例是20%,用Accuracy进行分析它们的分类准确率。首先,分别对γ和β进行大范围搜索,发现γ取值范围为{0.000 1,0.001,0.01,0.1,1},β取值范围为(0,2]时,NESSC方法性能较好。然后对γ和β的详细取值作具体分析,结果如图1和图2所示。
图1是改变γ初始值对算法结果的影响。当γ值为0时,不考虑聚类结果对节点嵌入计算的影响。随着γ值的增大,数据集Citeseer和Cornell的分类准确率逐渐提高,说明聚类过程的加入对计算节点嵌入有积极的影响。当γ值为0.01时,分类准确率最高。之后,又随着γ值的增大,分类准确率逐渐降低,这说明聚类结果的过多加入会影响节点特征的学习,从而导致学到的嵌入表示质量不佳。由此,在数据集Citeseer和Cornell的实验仿真中设置γ初始值为0.01。
图2是改变β值对算法结果的影响。当β值为0时,不考虑重构已知节点类别标签信息对节点嵌入计算的影响,此时学到的节点嵌入表示缺乏区分性。随着β值的增大,数据集Citeseer和Cornell的分类准确率逐渐提高,说明重构已知节点类别标签信息可以积极地影响节点嵌入的计算。对数据集Citeseer而言,当β值为1.8时,分类准确率最高,之后,又随着β值的增大,分类准确率逐渐降低;对数据集Cornell而言,当β值为1时,分类准确率最高,之后,随着β值的增大,分类准确率逐渐降低。这说明可以适当运用重构已知节点类别标签信息结果来提升节点嵌入表示的质量。因此,在数据集Citeseer和Cornell的实验仿真中,分别设置β值为1.8和1。
4结语
笔者提出的基于半监督聚类的网络嵌入方法NESSC,首先在计算节点嵌入特征的过程中强制节点进行k-means聚类,同时利用已知节点类别标签信息来指导其聚类过程,以此来保持网络的潜在社区结构。其次,通过重构已知节点类别标签信息来学习具有区分性的嵌入表示。在数据集Citeseer,Cora及WebKB上聚类和分类实验结果说明,NESSC融入节点类别标签信息提高了网络嵌入的质量。
现实网络中节点不仅包含复杂的拓扑结构信息,还拥有丰富的属性信息。下一步工作中,将在本文的基础上融入节点属性信息,进一步提高网络嵌入的质量。另外,异构信息网络因为包含不同类型的节点和边,可以更加完整自然地对现实世界的网络数据进行建模,后续也将对此展开深入探究。
参考文献/References:
[1]GOYAL P, FERRARA E.Graph embedding techniques, applications, and performance: A survey[J]. Knowledge Based Systems, 2018,151:78-94.
[2]齐金山, 梁循,李志宇, 等. 大规模复杂信息网络表示学习: 概念、方法与挑战[J]. 计算机学报,2018,41(10):2394-2420.
QI Jinshan, LIANG Xun, LI Zhiyu,et al. Representation learning of large-scale complex information network:Concepts,methods and challenges[J]. Chinese Journal of Computers, 2018,41(10):2394- 2420.
[3]HAMILTON W L, YING R, LESKOVEC J. Representation learning on graphs: Methods and applications[J]. IEEE Data Engineering Bulletin, 2017: 1709.05584.
[4]ZHANG Daokun, YIN Jie, ZHU Xingquan, et al. Network representation learning: A survey[J]. IEEE Transactions on Big Data, 2018:2850013.
[5]涂存超,杨成,刘知远,等. 网络表示学习综述[J]. 中国科学:信息科学,2017,47(8):980-996.
TU Cunchao,YANG Cheng,LIU Zhiyuan, et al. Network representation learning: An overview[J].Scientia Sinica (Informationis),2017,47(8): 980-996.
[6]WANG J. Locally linear embedding[C]// Geometric Structure of High-Dimensional Data and Dimensionality Reduction. Heidelberg:[s.n.], 2012:203-220.
[7]BELKIN M, NIYOGI P. Laplacian eigenmaps and spectral techniques for embedding and clustering[J]. Advances in Neural Information Processing Systems,2002,14(6):585-591.
[8]LE Q, MIKOLOV T. Distributed representations of sentences and documents[C]//Proceedings of the 31th International Conference on Machine Learning.Beijing:[s.n.],2014:1188-1196.
[9]PEROZZI B, Al-RFOU R, SKIENA S. DeepWalk: Online learning of social representation[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. NewYork: ACM, 2014:701-710.
[10]GROVER A, LESKOVEC J. Node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. NewYork: ACM, 2016:855-864.
[11]TANG Jian, QU Meng, WANG Mingzhe, et al. Line:Large-scale information network embedding[C]//Proceedings of the 24th International Conference on World Wide Web.Florence:[s.n.], 2015: 1067-1077.
[12]CAO Shaosheng, LU Wei, XU Qiongkai. GraRep: Learning graph representations with global structural information[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management.New York:ACM, 2015:891-900.
[13]WANG Xiao, CUI Peng, WANG Jing, et al. Community preserving network embedding[C]//The 31st AAAI Conference on Aritificial Intelligence. [S.l.]:[s.n.],2017:1-7.
[14]ROZEMBERCZKI B, DAVIES R, SARKAR R, et al. GEMSEC: Graph embedding with self clustering[J]. Computer Science, 2018: arXiv:1802.03997.
[15]CHEN Jifan, ZHANG Qi, HUANG Xuanjing. Incorporate group information to enhance network embedding[C]//Proceedings of the 25th ACM International on Conference on Information and Knowledge Management. New York:ACM, 2016:1901-1904.
[16]TU Cunchao, ZHANG Weicheng, LIU Zhiyuan, et al.Max-margin deepwalk: Discriminative learning of network representation[C]// Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence. NewYork:[s.n.], 2016: 3889-3895.
[17]KINGMA D P, BA J. Adam: A method for stochastic optimization[J]. Computer Science, 2014: eprint arXiv:1412.6980.
[18]STREHL A, GHOSH J. Cluster ensembles: A knowledege reuse framework for combining multiple partitions[J]. Journal of Machine Learning Research, 2003, 3(1): 583-617.
[19]周志華. 机器学习[M]. 北京: 清华大学出版社, 2016.
