基于流形学习的自适应反馈聚类中心确定方法

李天龙+吴晟+吴兴蛟+周海河+曹敏+王昕

引言

现如今，数据存在于我们生活的每一个角落，在大数据快速发展的今天，数据挖掘成了进行数据分析的有效途径，同时也是获取数据信息的关键。

在海量数据下进行研究要求对于数据规律的探索，数据的聚类就显得尤为重要，目前对于聚类算法的研究大致归纳为五大类，分别基于分割、层次、密度、网格和模型。上述的许多聚类算法都在实际中得到了较好地运用，同时也取得了一些效果，但是这些方法都存在一个共同的不足就是需要人工调参。这种方式将给自动化生产编程带来一定限制。

正是由于存在上述问题，寻找一种能反馈调节聚类参数的算法就有其必要。

本文在对谱聚类算法进行探究以后，提出一种基于目标条件的反馈聚类。这种聚类方式对于大多数线性流形聚类参数选择具有一定适应性。

1相关理论

流形学习聚类随着高维大数据问题被提出，经过几年的研究与探索，人们提出了大量的流形学习的理论与算法。比较典型的算法有ISOMAP、LLE、拉普拉斯算子特征映射（Laplacian eigenmaps）、最大方差展开（MVU）、局部切空间分析（LTSA）等。聚类，顾名思义就是根据样本间相似度，将数据分成不同组。其中谱聚类是流形聚类中具有代表性的一种聚类方式。

谱聚类主要由以下四个步骤步组成：

Step1，构建相似度矩阵，即计算每个数据点与其余数据点的相关系数。

Step2，计算拉普拉斯矩阵，并将其进行归一化；

Step3，生成最大的k个特征值和对应的特征向量；

Step4，采用k-means方法对特征向量进行聚类。

2模型建立

提出的反馈聚类算法主要基于谱聚类实现，聚类数目首先随意指定，在一次聚类结束后将聚类结果代入目标中验证，如果未达到目标阈值则调整聚类数，进行新的聚类，直到所得聚类结果满足聚类目标。得到结果后经过多次迭代后计算聚类数的加权平均以后得到的聚类数。反馈聚类流程图如图1。

2.1数据集设置

谱聚类的前提是构造相似矩阵，这就要求将不同构型或者不同维数的数据进行处理。一般根据特征值或者矩阵实际运用得到新的n阶方阵。

2.2构造相似度矩阵

基于谱聚类的方法是建立在谱图理论基础上，其基本思想是将样本看作顶点，样本间的相似度看作带权的边，从而将聚类问题转为图分割问题，即找到一种图分割的方法使得连接不同组的边的权重尽可能低，组内的边的权重尽可能高。与传统的聚类算法相比，其具有能在任意形状的样本空间上聚类且收敛于全局最优解的优点。可根据公式1构造聚类相似矩阵。

2.3反馈谱聚类

建立如下谱聚类模型：

Step1：输入一个MN的矩阵w，即w中一共包含N个数据点；

Step5：计算矩阵L的归一化矩阵E的k个最大特征值及对应的特征向量，形成一个N K的特征矩阵，记为Q；

Step6：对特征矩阵Q做k-means聚类，得到一个N维向量c，c中分别对应相似度矩阵w中每一行所代表的对象的所属类别，即最终的聚类结果。

Step7：验证聚类结果包含目标最大子集数是否大于阈值，大于阈值则得到结果，否则调整聚类数执行Step6。

Step8：多次迭代算法得到聚类列表ListC。

2.4计算加权平均

得到列表ListC以后，针对列表中的数求加权平均数成为新的聚类数。如公式5。

3实例验证

3.1数据集设置

实验数据取自2016年研究生数学建模B题数据。

先从数据清洗，缺失值处理以及数据变换方面进行预处理。

数据清洗，主要通过数据统计查看有无存在ATCG四种碱基以外的其他构成。寻找到除了ATCG以外，数据还存在I和D，后来根据官方文件修正为T和C。

缺失值处理，使用函数查看数据有无空值，最后发现无缺失现象。不必进行插值以及增补。

数据变换，由于数据直接使用ATCG字符难以计算距离，所以对其进行编码形成编码文件。

首先将文件gene info导入后根据每一条基因对应的位点构建合适的碱基对矩阵，构建相似矩阵。

附件gene info文件夹中有300个dat文件。每个dat文件数据表示每个基因的位点信息，每个dat文件表示一个基因。和附件文件genotype.dat中的位点信息相结合进行数据挖掘和分析。附件所给出的数据格式不能满足数据挖掘的要求，所以进行数据预处理。

将附件给出的300个文件合并导入EXCEL文件中，并对基因从上到下依次编号。局部结果如表1所示。

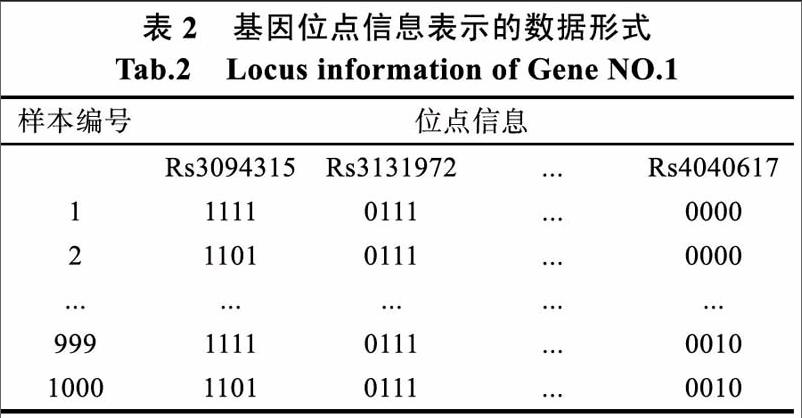
数据的初级预处理得到如表2所示的数据格式，表的第一列为300个基因编号，其余列为基因的位点信息。由于基因含的位點数目不同，所以在基因信息和位点信息合并时需要对缺省基因进行补缺省值得处理，采用补0。把基因位点对应表和genotype.dat导入MATLAB进行数据的第二步数据预处理，把两个数据相互融合。以编号为l的基因为例，融合后得到如表所示的数据形式。

300个基因的数据格式如基因1位点信息格式。经过两步数据的预处理，数据的各项要求满足数据挖掘的信息。

3.2模型求解

硬件环境：2.6 GHz CPU，8G内存。

软件环境：Windows7，matlabR201 3a。

根据反馈聚类操作流程，如图2，在1000"9446高维矩阵下，设定参数最大子集阈值为4，迭代次数为100。使用MATLAB实现流行聚类算法，本文采用谱聚类方法对数据进行100次聚类分析，每次聚类会产生一种聚类分组，从基因组中选取满足致病基因覆盖点大于等于4的基因组作为候选组。执行完成算法后会产生100组候选数据。使用统计学方法统计100个候选组基因出现次数最多的基因。并计算中位数以及加权平均数描绘其实时曲线，进行对照。

4实验结果与分析

迭代一百次以后，统计聚类次数，得到各次聚类曲线图，分别计算聚类集合中位数以及聚类集合加权平均数，如图3所示。

观察曲线可以初步得知加权平均数更能体现统计规律。

分别将得到的中位数以及加权平均数进行聚类。得到聚类后数据与统计数据对比，对比图4，图5中包含统计值的数量。

最后对比得出，使用加权平均分类数得到的聚类集合更能体现统计数据。

5结论

通过反馈谱聚类方法迭代后的中位数以及加权平均数来确定聚类数，改善了流形聚类中聚类数难以确定的难题，通过不断的适应目标从而调整聚类数，然后再通过不断迭代后的加权平均数来得到最后的聚类值。再和得到的中位数进行聚类效果的比较，这种方式下得到的结果是：使用加权平均数获得的聚类数更加锲合要求。endprint