转化思想在数学解题中的运用策略

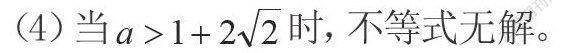
【摘 要】转化是一种重要的解题思想，是一种有效的思维方式和最基本的思维策略。转化思想就是指在研究和解决问题时，采用某种方法和手段将问题通过变换使之转化，让问题最终得以解决的一种思想方法。转化思想的本质，就是实现由难到易、由繁到简、化抽象为具体、从未知到已知等。本文探讨了在数学解题过程中常用的几种转化策略。

【关键词】转化思想;数学解题;运用策略

【中图分类号】G712  【文献标识码】A  【文章编号】1671-8437（2019）28-0024-03

数学家G·波利亚在《怎样解题》中说过，数学解题是命题的连续变换[1]。苏联数学家雅诺夫斯卡哑在阐述解题意味着什么时说：“解题——就是意味着把所要解决的问题转化为已经解决的问题。”从这个意义上说，解题就是转化，解题的过程就是运用相应的方法和技巧把待解决的问题转化为已解决问题的过程。由此可见，转化思想在数学解题中的重要作用。

1   结构转化

有很多数学问题，在对题目的数式结构进行认真分析和研究后发现，可运用相应的数式变换方法，把所求问题的结构转化为已知或熟知的结构，以达到化未知为已知，化陌生为熟悉。这一转化策略在数学解题中应用

广泛。

例1.求函数的最值。

分析：通过观察发现，可利用公式对题目中函数的解析式进行结构转化，将问题转化为关于的一元二次函数的最值

问题。

解：函数，可化为。因为，所以当时，有;当时，有。

例2.在代数式的展开式中，常数项为____。

解析：分析后发现，可将题目中代数式的结构转化为

，前面一部分的展开式中不含常数项，后一部分的展开式中的常数项为-5，所以答案为-5。

2   数形转化

在解决问题时，根据题目中的数式特征，把相应的数量关系转化为图形的性质，或者把图形的性质转化为数量关系，从而使复杂问题简单化，抽象问题具体化。

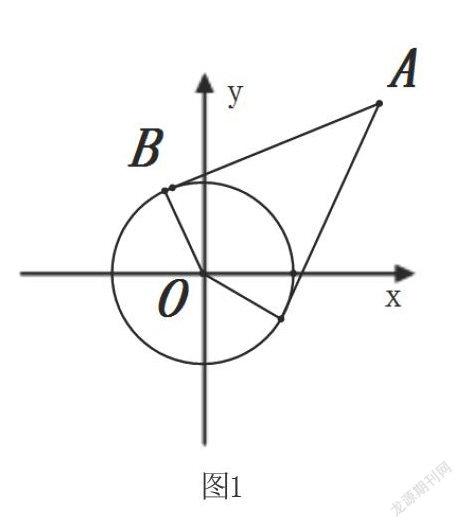
例3.已知，求函数的值域。

分析：由函数表达式的结构特点很容易联想到直线的斜率公式。因此，原问题可转化为求直线斜率的取值范围。

解：可看作是点与单位圆上的点连线的斜率，如图1，设直线的方程为，联立方程消去得，令，解得，结合图形得直线斜率的取值范围是，即所求函数的值域为。

3   正反转化

当正面解决问题遇到困难或解决方案相对繁琐时，可试着考虑问题的反面，以探求解决方案，这就是“正难则反”的转化策略。若题目中出现“至多”“至少”等存在量词，通常可考虑采用这一转化策略。

例4.已知非空集合中至少有一个元素小于零，求实数的取值范围。

分析：集合中的元素即為关于方程的实数根。因此，题意为方程有实数根且至少有一个负的实数根。若是从正面入手，则要对所有可能情况进行分类讨论，较为繁琐.而若考虑其反面（即没有负根），则要简单得多。

解：由解得或

，这是集合非空（即方程有实数解）情况下实数的取值范围。

当方程有两个非负实根时，有

解得，

所以非空集合中至少有一个元素小于零时实数

的取值范围是。

例5.从5名男生、3名女生中选派4人参加某项社会实践活动，若要求至少有1名女生，则不同的选派方案种数为（   ）。

A.28     B.65     C.56     D.60

解析：由总的选派方案种数，减去女生都不参加（只有男生参加）的选派方案种数得，选B。

4   动与静转化

数学中的动态问题反映的是运动变化中的数量和位置关系，是解决问题的一个难点，学生常常感到无从下手。面对此类问题，首先应明确动与静是相对的，可以相互转化。接下来关键是抓住图形运动的规律，或者是动点的运动轨迹，也就是找到运动中的不变性，以静制动，将动态问题转化为静态问题来解决[2]。

例6.在坐标平面上有一运动着的梯形ABCD，AD∥BC，∠C=45°，∠A=90°，AB=AD=，梯形在OA+OB=4的条件下运动，求原点O到直线CD的最短距离。

分析：题设中的条件概括起来有两个：一个是运动的梯形ABCD，另一个是其运动的条件OA+OB=4。该梯形的结构已经清楚，解题的关键是紧扣第二个条件。数学公式OA+OB=4的含义让我们想到椭圆的定义，但问题是，这里A，B是动点，O是定点。怎么办？其实只需认识到“动”和“静”是相对的，可以相互转化，问题便可以迎刃而解。

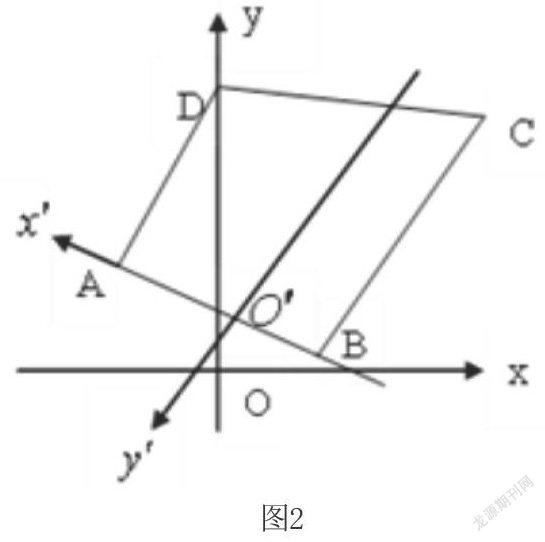
解：这里视梯形静止而原点O是运动的，则由OA+OB=4，AB=可知，动点O的轨迹是以A，B为焦点的椭圆。如图2，建立以AB中点O′为“原点”，AB中垂线为轴的新坐标系，则CD的直线方程为

。动点O的轨迹方程是，设O在新坐标系下的坐标为，则O到直线CD的距离为≥，当且仅当时，原点O到直线CD的距离最短，为。

5   整体与部分的转化

5.1  整体化为部分

整体由部分组成。在解决问题时，如果研究对象包含多种情形，则需要把研究对象化整为零，通过各个击破，来实现整体问题的解决。

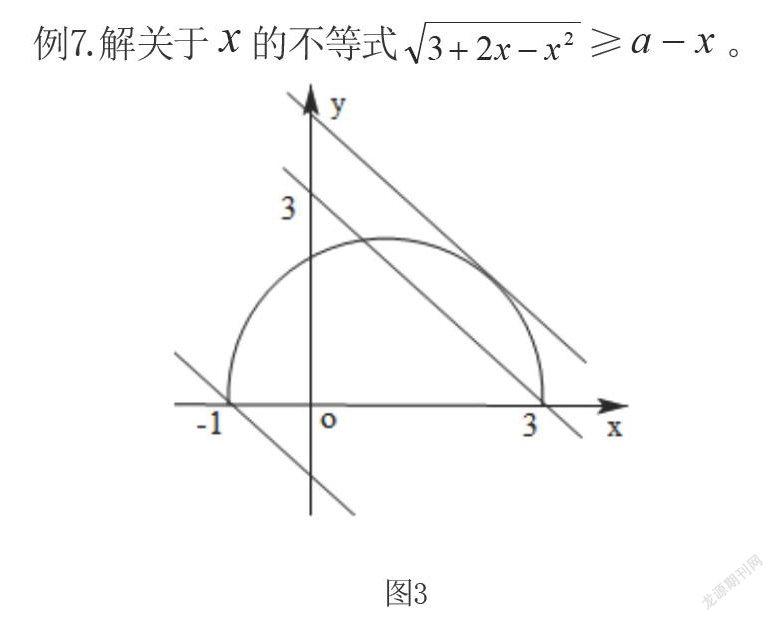
例7.解关于的不等式≥。

分析：这是一个含参数的无理不等式，因此要考虑参数取值的不同情形下不等式解的情况。

解：在同一平面直角坐标系中画出函数和的图像，即一个半圆≥和一条直线（如图3），为直线在轴上的截距，直线和半圆相切时，算得，根据直线与半圆的交点情况，结合的范围，得：

（1）当≤时，有≤≤3;

（2）当≤3时，解方程得直线与半圆交点的横坐标，从而得不等式的解为≤≤3;

（3）当≤时，≤≤;

（4）当时，不等式无解。

5.2  部分化为整体

当孤立地考虑一个数学问题而难以解决时，不妨对研究对象展开关系联想，尝试将研究对象视作某一更为熟悉的“整体”的部分，从整体上把握与处理问题，往往能化陌生为熟悉，化难为易。

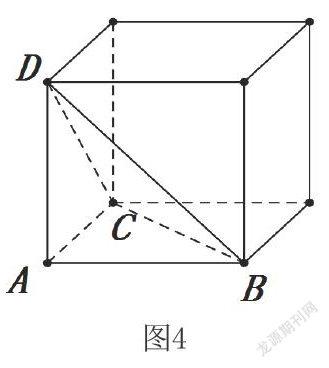
图4

例8.若三棱锥的三个侧面两两垂直，且侧棱长均为2，求其外接球的表面积。

分析：本题的关键是怎样得到三棱锥的外接球，进而求得外接球的半径长。单独考虑三棱锥的外接球是很难想象出的，而若根据题中三棱锥的特征，将该三棱锥放在一个相应的正方体中来考虑，则可将三棱锥的外接球问题转化为熟悉的正方体外接球问题。

解：把满足题设条件的三棱锥“补”成如图4所示的正方体，则三棱锥的外接球即为图中正方体的外接球。求得正方体外接球的半径为，故所求三棱锥外接球的表面积为。

转化思想是数学解题中一种重要且有效的思维方式和思维策略。鉴于其在数学解题中的重要作用，教师在解题教学过程中，应注重引导学生运用转化思想解决问题，掌握常用的转化策略，提高解题能力。

【参考文献】

[1]G·波利亚.怎样解题[M].科学出版社，1982.

[2]朱其超.借助数形结合简化和避免分类讨论问题[J].中学数学教学参考，2012（10）.

【作者简介】

朱其超（1973～），男，安徽宿州人，讲师，学历：硕士，研究方向：数学课程论、数学学科教学论。