2021年PISA数学

[美]桑贾伊·马汉贾恩 [波兰]兹比格涅夫·马齐尼亚克 [美]比尔·斯密特 [美]查尔斯·菲德尔 王铭军 盛群力

摘 要：数学是理解世界、公民身份和经济增长的基石。为了满足全社会对教育的需求，21世纪教育应该注重对知识理解的深度和多样性的培养。PISA关于数学能力的测试中，最重视学生运用数学推理来解决问题的能力。我们建议扩展数学过程的描述（表述、应用、解释、评估），并在PISA数学框架内确定这些处理过程为数学建模的主要组成部分，其中有七个最常用于寻找正确推理方法的推理工具：比较、比例推理、应用乘法量表、拆分、归并、由简入繁、概率推理和逻辑推理。PISA数学的素养领域涉及形状与空间、变化与关系、不确定性与数据、数量等，还要特别注意创造性思维能力、品格和元认知技能的培养。

关键词：数学素养与能力;PISA数学框架;推理工具;问题解决能力

中图分类号：G434 文献标志码：A 文章编号：2096-0069（2019）05-0083-010

收稿日期：2019-06-18

一、引言——数学一直很重要

數学是理解世界、公民身份和经济增长的基石。

全球教育体系已经逐步适应了工业时代的需求，正在为迎接创新时代的来临做准备，为促进学生在快速转型的过程中获得成功而努力。19世纪后期，社会和人力资源需求的迅猛增长促进了课程的最近一次重大变革。21世纪与19世纪的教育课程完全不同，为了满足全社会对教育的需求，21世纪教育应该注重对知识理解的深度和多样性的培养。

数学是以下各领域的基础：以科学、技术和工程为创新原动力的经济发展;理解现实世界与公民身份。

PISA（国际学生评估项目）对数学素养给出了如下精确描述：①“一个具有数学素养的人，能认识和理解数学在现实世界中所起的作用，能利用数学作出有根据的判断和决策，是一个具有建设性、参与意识和反思能力的公民。”

科学/技术/工程/数学（STEM）是课程的重要因素，尤其是在当今世界范围内供不应求，STEM教育需求很大，而STEM素养被认为是通过创新促进增长的关键驱动力。①数学是STEM的基础，也是培养创新者的关键要素，更应受到格外关注。

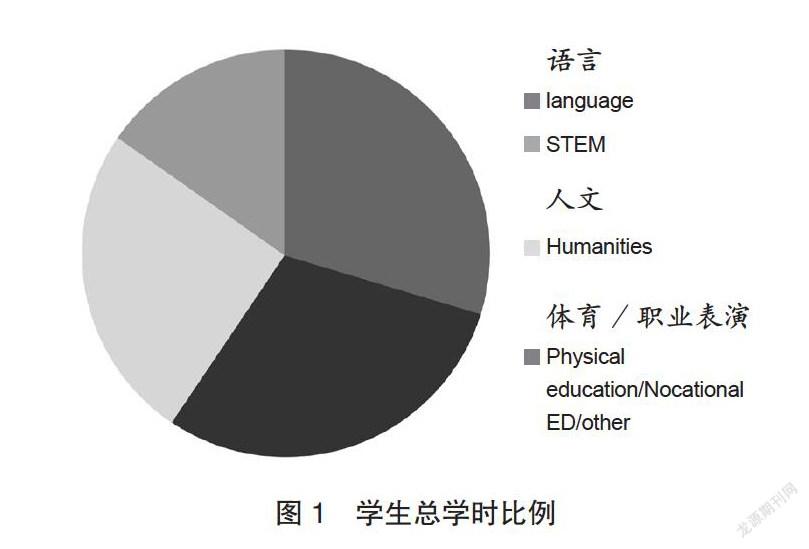
如图1所示，在目前的教育系统中，STEM课程占学生总学时的比例——在经合组织（OECD②）调查的国家中约占30%的学时：

进一步分析可知，数学在STEM课程总学时中约占45%的学时，或者大约占总的授课时间的11%。（而对于经合组织国家大约占15%的时间，每年为此课程约花费2.35万亿美元。③）

二、应对2021年PISA的改进理由

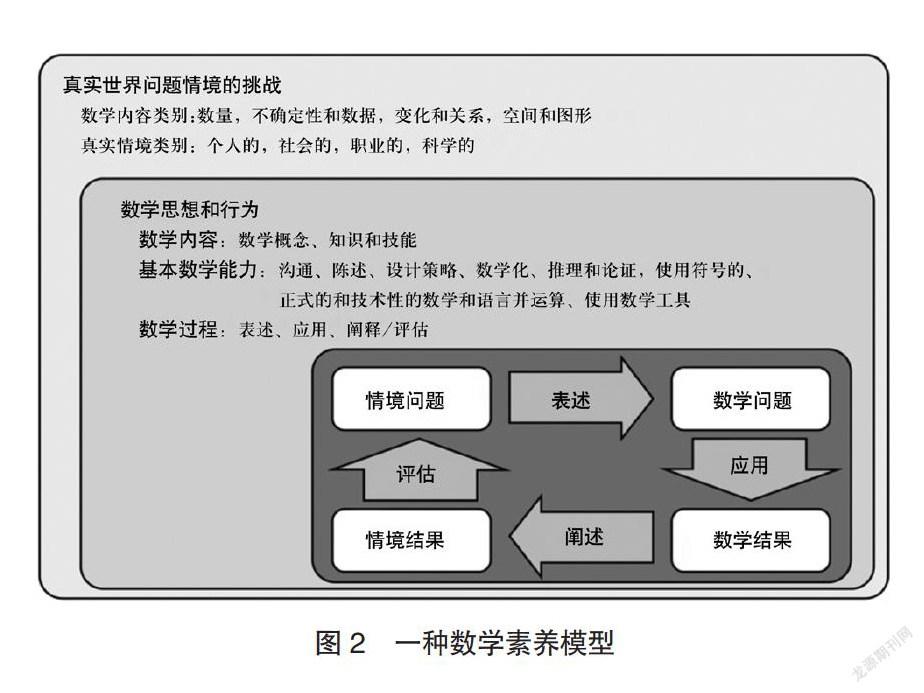
我们将描述基于PISA 2015数学框架的非常有效和有意义的概念，并作为本文的参考（如图2所示）。

（一）数学推理是理解世界的钥匙

正如PISA数学框架中定义的，数学素养的一个重要方面是个人的数学推理能力。

从数学本质来说，任何数学问题都离不开数学推理。一些复杂问题需要分解成一系列简单问题，然后再求解。但是，即使将问题简化后能产生用“心算”来计算的解，也要利用数学推理来证明这些解的合理性。数学难题一旦被正确演绎的数学推理所解决将会给世界带来创新的动力：我们得出了这个不可辩驳的永恒真理。

在日常生活中从现有事实推演出合乎逻辑推论的能力是至关重要的，因为这种能力可以用于数学之外的情境。当我们想要在事实的基础上准确地证明我们的观点时，就会运用数学课上学过的逻辑推理：一个结论暗含了另一个结论，而一个精心挑选的反例可以将虚伪对手的论据化为灰烬。

在提出自己的观点或分析他人的观点时，具有建设性、参与意识和反思能力的公民会运用数学推理的能力做出有根据的判断和决策，这是至关重要的（PISA 2015数学框架草案，第5页）。因此，数学教师应特别注意培养学生这一能力。培养这种能力比教学生用常规方法解决标准数学问题要困难得多。在没有老师直接参与的情况下，学生想要取得成功，就需要构建一系列论据链。当学生将这种训练转变成他们的习惯时，不仅会主动表达他们的观点（例如，通过点击Facebook上的“喜欢”），而且还会辩护和捍卫自己的观点。④

（二）全球就业能力需求的变化

几十年来，随着对数学需求的不断增长，数学已经出现了许多新的分支和主题，这反映在表1的经合组织工业调查中;①简言之，现代工业需要不同的数学，现代数学的分支已经超越传统的分支，如算术、几何和代数。今天与数学相关的分支和主题已经远远超出了15年以前的范围。

显然，对测量师和木工的需求表明当时社会需要精通三角函数这一数学分支的人才，然而，现代社会对他们的需求量已经下降了，取而代之的是对数据分析人才的需求。谷歌（Google）首席经济学家哈尔·瓦里安（Hal Varian）曾表示：②“我一直在说，未来十年最令人羡慕的人将是统计学家。大家认为我是在开玩笑，但谁会想到计算机工程师会是20世纪90年代最诱人的职业呢？”

三、清晰的推理及过程

PISA关于数学能力的测试中，最重视学生运用数学推理来解决问题的能力。这种推理能力的测试题目，对参与的学生来说，通常是困难的。许多学生不能给出预期的对问题分析的一系列论据链。

尽管如此，许多未通过测试的学生仍然试图解决这些测试题目，因为他们喜欢做这些有趣而富有挑战性的问题，不喜欢那些只需要简单计算的题目。正因为如此，由于数学推理对数学素养的重要性，在未来的PISA测试中评估这些试图解决问题的尝试③是非常重要的，以奖励那些使学生能接受正确教育的教育体系，通过认真筛选将要构建的项目，使学生利用正确的推理方法来解答，实现对学生数学推理能力的培养。

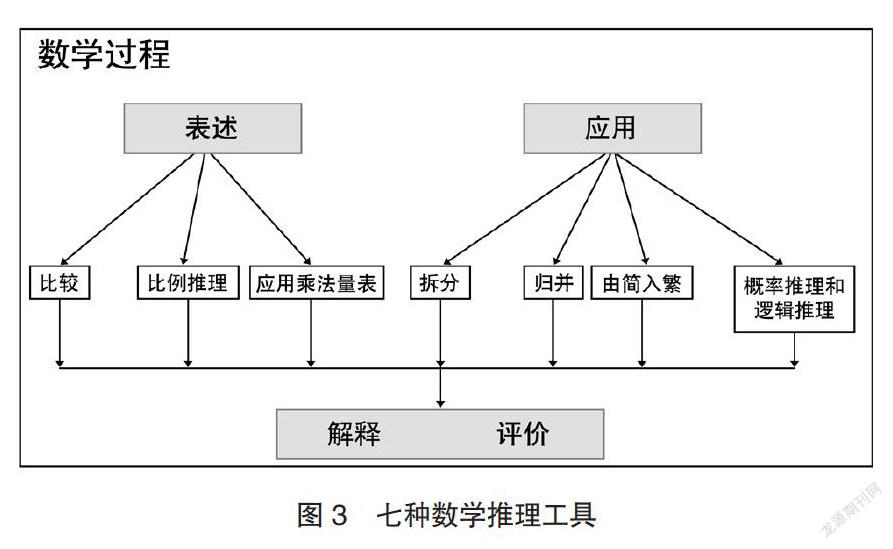
因此，我们建议扩展数学过程的描述（表述、应用、解释、评估），并在PISA数学框架内确定这些处理过程为数学建模的主要组成部分，其中有七个最常用于寻找正确推理方法的推理工具，④如图3所示。

学生给出的解答中对上述工具的成功运用可以衡量他们使用数学推理方法解决问题的能力。⑤通过这种方式，学生数学推理能力的测量将变得更加精确。

2015年PISA数学框架草案规定：“2015年PISA数学测试题目将分布于以下三个数学过程之一：1.以数学方法表述问题情境;2.运用数学概念、事实、过程和推理;3.解释、应用和评估数学结果。”

请注意，解释原始现实问题的数学化结果的过程，以及从有用性角度来评估前面结果的过程，在图2中是分开呈现的，在这里放在一起考虑。这是因为它们有一个共同的目标：重新评估数学模型的约束条件，以确定所获得的解答是否合理，或者是否有必要继续修改该模型。

当以数学方法解决问题时，人们经常会面对量化的数据。单独的数量是没有任何意义的，它的意义来自与其他数量的关系。为了识别这些联系，我们有三个基本工具：比较（comparison）、比例推理（propor-

tional reasoning）、应用乘法量表（applying multi-plicative scales）。在利用数学方法进行公式化过程中，使用这些工具的能力是非常重要的。

比较：当一个数量与另一个相关的数量进行比较时，这个数量才有意义。例如，每年1万亿美元的货币利率本身意义不大，但如果它是政府预算或GDP的一部分，那么它就有意义了。另一个例子：在一篇报纸文章中仅仅读到带一个数字的句子，例如“100万粉丝走上街头庆祝体育团队的胜利”（波士顿报纸上经常出现）传达的信息很少。只有将100万与波士顿和内城区的总人口（约为100万）进行比较时，这个数字才有意义（因为令人非常难以置信）。

比例推理：通过比较产生比率。理解比率变化之间的相关性（例如，长度加倍可获得四倍于原来的面积），即比例推理的实质，对于利用数学方法描述现实世界问题是至关重要的。在PISA框架之下，比例推理为PISA问题的解答提供了简单的方法。

应用乘法量表（包括指数增长）：下一个工具是以比率为单位进行计数——例如：太阳质量大于地球质量的多少可以用以2（或10）为底数的指数形式来表示。基于数量有较大范围的差异，使用对数和指数尺度来表示数量。对数尺度能表示宇宙中长度、时间和能量的巨大的动态数量范围。在人类社会中，指数增长模型有助于模拟人口、经济、流行病传播或资源利用的增长。

由于模型的复杂性，在数学模型中运用数学概念和公理来推理也很困难。学生可能会被模型中出现的许多数学符号的含义搞得晕头转向。因此，简化模型的能力是数学过程中运用阶段的一个非常重要的方面。有四种基本的简化工具，可帮助我们以可理解的方式表达现实世界的复杂性：拆分（divide and conquer）、归并（lumping）、由简入繁（consider first easy cases）、概率推理和逻辑推理（Probabilistic and logical reasoning）。

拆分：这个工具很久以前就被广泛使用了。我们将难题分解成许多容易解答的部分。例如，在计算24+ 38时，学生可以将38分解为6和32，然后先计算24 +6= 30再计算30+32=62。对于PISA年龄的学生来说，可使用拆分来推理的一大类问题就是所谓的费米问题。例如：“一条繁忙的铁路能运送多少乘客（每小时运送乘客数）？”为了解决这个问题，可将此问题化简为该铁路每小时有多少列车通过，每列车有多少车箱，每节车厢有多少乘客。费米问题有时也需要进行近似估算，这可由下一个推理工具——归并来实现。

归并：通过对数字的舍入运算或利用简单形状逼近复杂形状的方法，忽略不太重要的细节问题，解决主要问题。因此，可将复杂的问题转化为简单的问题。例如，登富士山问题要求学生计算一个人步行的长度，这个人走了22，500步，总路程9公里，登上了富士山。简单的归并计算给出了近似的估计：大约20，000步走了大约10，000米，意味着每步约0.5米。

由简入繁：当问题仍然太难时，可利用该问题的若干特例来理解这个问题。例如，在求解数学推测时，我们首先用n=0和n=1的特例来尝试一下。或者，在个人和社会背景下，抵押贷款的利息就像年金保险一样，在某种特殊情况下，它的利率乘以贷款期远远大于1;或者，在另一种特殊情况下，抵押贷款分期偿还，它的利率乘以贷款期远远小于1。在每一种特殊情况下，支付额度是容易计算的，并且这个计算过程比一般的情况更容易理解。

概率推理和逻辑推理：数学过程中的完整“推理”流程要求利用概率推理或逻辑推理。利用概率推理来表示那些不确定的知识——特别是利用概率来假设事件发生的可能性。如：贝叶斯定理，它与证据和可信度有关，它是通过计算收集来的数据和证据来推理不确定的知识，这些知识用概率来描述它的改變。概率推理包括逻辑推理：在概率为0（假）或1（真）的简单（极端）情况下，概率推理简化为逻辑推理。

解释和评估是由原始现实问题引出的，并通过比对数学推理所获得的结果与现实生活的实际约束之间是否存在对应关系。从数学推理计算中得到的数字必须与它所表达的实际情况数据相吻合。这样做的同时，几乎所有前面提到的数学过程都可以得到有效利用。例如，我们经常发现学生不符合现实情况的解答：有人以50公里/小时的速度行走，或者200人同时进入电梯。如果这些学生养成了应用“比较”“比例推理”“量表”或“归并”算法的习惯，他们会很容易发现他们不符合现实情况的解答是不可信的。应用简单的逻辑也可以很容易排除其他类型的错误，例如坐在教室里的学生人数为负数。

四、知识相关性

持续关注现有重要的知识领域，纳入新的重要/相关领域。

弗莱登塔尔研究所在描述“工作场所数学”时说：①“在许多职业中，最重要的是数字、数量、估算、数据处理和数据的不确定性;其次是空间和形状、关系、变化、公式。”

英国皇家学会描述了以下工作场所的数学要求：②数学建模（例如自来水公司的能源需求、三明治的成本等）;软件使用，问题应对（例如采油、污水排放等）;成本核算（分配、争议管理）（例如医院保洁承包合同、铁路管理等）;业绩和比率（例如保险比率、血糖指数等）;风险（例如临床管理、保险等）质量/ SPC控制（例如家具、机器停产时间、轨道偏差等）;

更一般地说，美国国家科学基金会已声明：③“更加重视估算，心理数学……”“不太重视纸张/铅笔的演算……”“……代数，几何，预科微积分和三角学中的内容需要精简，为重要的新主题腾出空间。”“必须引入离散数学，统计/概率和计算机科学。”

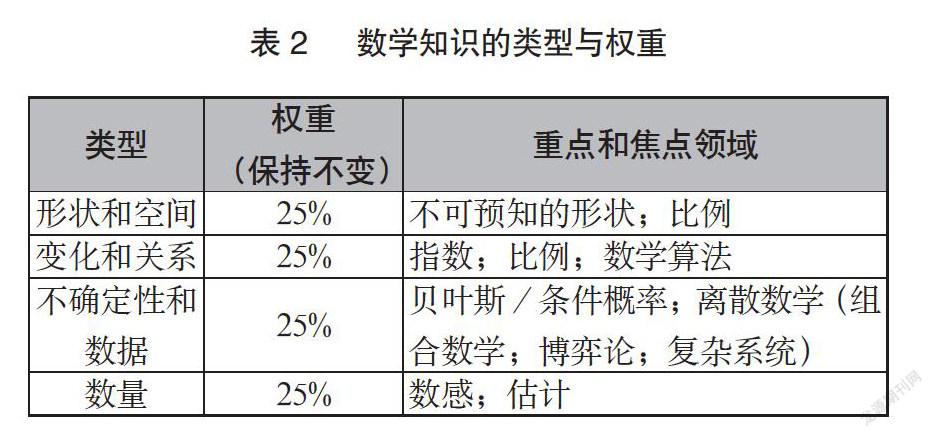
基于本文至此所涉及的所有讨论，针对相关数学知识的领域需求，以及个人、社会和职业④需求（同时尊重PISA分类和聚焦）的重要性，特提出以下建议（表2、表3）。

上述内容对于重点领域的定位，与先前描述的推理/过程技能是非常一致的，并成为数学过程不可分割的部分，并且提供了解决这些领域问题所需的工具，特别适合于应对现实世界的各种情境。

五、培养能力（技能、品格、元学习）

注意：对于批判性思维（技能），上面关于显性推理的部分已经描述了一些需要学习的高阶思维技能，此外还有技能和元学习。有关创造力（非规范性答案）和元认知，CCR（美国课程再设计中心）在数学创造力和元认知方面确定了以下发展过程：使用标准解题思路解答练习和问题;使用非标准解题思路解答练习和问题（创新思维）;发现新的现实问题，并使用标准和非标准解题思路解答（创新思维）;创建新问题，并使用标准和非标准解题思路解答（创新思维）;创建新的问题类（元认知扩展）并探索可解性。

（一）衡量数学思维中的创造力

学习数学的学生能够将他们学到的数学知识、技能和工具灵活地应用于现实中面临的各种问题和挑战，是这些学生应该达到的基本学习要求。这也是PISA数学素养中明确规定的基本要求之一。将知识灵活地应用于新情况和新问题通常包含认知方法的创新，尤其是非常规方法的创新。这被认为是教育/学习难以攀登的高峰。这种灵活应用数学知识的思路是与创造性思维和解决数学难题的能力密切相关的。

教育工作者在实现登顶“珠峰”的过程中面临着巨大的挑战：学生如何才能灵活地将他们的知识从已知领域迁移并应用到未知领域？以标准解答来评估学生知识的传统多项选择题，这些题包含基本算法和概念的使用，这样的题目是不可能训练出能灵活运用知识并具有创造性思维的学生的。要想培养创新思维的学生，这些题目应该要求学生解释他们是如何用一种或多种方法来思考解决这个数学问题的，或者要求学生说明包括非常规的解题方法在内的几种不同的解题方法。这类题目已成功应用于衡量教师在数学教学方面的知识技能①。以下题目原型展示了一个例子（如例1所示），用以说明这些题目在尝试评估学生对数学情境的创造性方法时可能会是什么样子。

例1

下面关注创造力的例子，要求受试学生评估四个样本学生分别给出的解答。学生Allan的解答很可能被认为是标准解答，但学生Cristine的解答也是正确的。受试学生必须根据提供的解题标准来评估每个人的解答。这要求受试学生不能只是简单地选择标准解答，还要评估非标准解答。因此，他们必须运用他们的知识来评估所给出的每个解答，以便找出正确的选项。只有一个选项是正确的（选项6）。

C是线段AB上的点。ACM和BCN为等边三角形，请问：AM=BM是否成立？

四位学生所作图如图4所示：

哪位学生或者哪几位学生的图形满足上述条件？

（1）Allan的图

（2）Betty的图

（3）Cristine的图

（4）Dave的图

（5）Allan和Betty的图

（6）Allan和Cristine的图

（7）Betty和Dave的图

（8）全部四个人的图

有些人②将创造力定义为能利用现有信息做出创新决策，在PISA案例中现有信息包含定量的信息。下面的示例（如例2所示）包含这种情况：

例2

国防预算项目：③

在某个国家，1980年的国防预算为3000万美元。该年度的预算总额为5亿美元。次年，国防预算为3500万美元，而预算总额为6.05亿美元。两个预算期间的通货膨胀率为10%。

（1）邀请某人为和平协会举办讲座。他们想解释一下这一年国防预算有所减少。如何解释才能说明预算的减少。

（2）邀请某人到军事学院演讲。他们想声称这一年国防预算有所增加。如何解释才能说明预算的增加。

（二）涉及元认知的数学能力

在下面的例子（如例3所示）中，要求受試学生评估由三名样本学生给出的问题解答。为了正确评估这些解答，学生必须理解三个概念：自然数的定义、数字平方的定义以及如何确定概率。一旦受试学生确定了自己认为正确的解答（Monica的方案），就需要解释余下的两个自己认为错误的解答，并说明其错误的原因。这要求受试学生反思每个学生给出的推理，并找出导致对问题不恰当解答的潜在错误推理。这类题目要求学生思考不同的解题方案，并提出假设，捕捉不同解题方案中所体现的思想——元认知任务。

例3

John选择了一个任意自然数，然后加以平方，取平方后最后一个数字，这个数是1的概率是多少？

下面是三个学生的回答：

Lisa：总共有10位数。每一个数字成为最后一位数字的机会相同，因此概率为1/10=10%。

Monica：个位数的平方只与被选择的自然数的个位数的平方有关。个位数的平方只有10个数字可能：1，4，9，6，5，6，9，4，1，0。因为有两个1，所以概率为2/10=20%。

Silvia：概率無法确定，因为有无数多的自然数，无法测试所有可能性。

以上答案中，哪一个最恰当（只选一个答案）？

Lisa…………………（）

Monica………………（）

Silvia…………………（）

下面哪一个选项最恰当地表示了其他两个学生存在的问题（至多两个选项）：

（1）不理解平方是指什么

（2）不理解自然数是指什么

（3）没有考虑到最后一位数已经确定是1了

（4）觉得题目太难放弃了

（5）没有考虑恰当的自然数

（6）不理解概率是指什么

有关品格（修复力/坚毅）的数学能力，请参阅下面有关日志数据的部分。

六、创新工具

PISA近期最重要的教学方法变化是从纸质评估过渡到基于计算机的评估（CBA），大多数PISA的参与国在2015年已经实现这一转变。这项创新变化提高了评估的可靠性，并能持续与社会数字化保持同步。在数学素养的评估中，CBA的出现为衡量学生数学推理能力提供了新的途径。

（一）数学中的计算

注意：这不是计算机辅助教学！也不是计算机科学或编程。①

从本质上讲，数学是一项解决问题的思维活动。根据PISA 2015数学框架草案，数学是一个不断迭代的循环过程：问题定义—数学化转换—结果计算—解释。原来数学教育和评价都专注于利用纸质化来实现这一循环过程。随着计算机在数学上应用的增长，这一循环的关注点发生了转移，为PISA提供了一个创新的机遇——引入新的评估方式来衡量更广泛的数学技能。

在计算机的创意编码环境中可以构建数学技能评价的交互式场景，计算机能以受控方式自动评价数学技能的完整循环。基于云计算的数据传递确保了对数学技能评价的安全便捷，并确保每位学生可以获得唯一和真实的测试数据，想要在传统纸质版本中实现这样的测试几乎是不可能的。团队协作技能也能在计算机模拟的逼真情境下得到充分的训练。

例如，使用短闭合问题将被评估学生的能力抽象成编码，就可实现自动评估。这样的话，通过更广泛地拓展任务，以端对端的方式，沿着完整问题的解决路径，去评估开放性问题也是可能的。任务示例见表4、表5（见下页）。

（二）使用日志数据

在评估过程中分析学生采取的步骤和思路有助于了解学生如何尝试解答问题，如应用数学推理，遵循反复学习原则，通过不断尝试或简单地猜测来解答多项选择题。为此，应设计开发这样的数学PISA项目，项目的解答既可以通过一个较长时间反复的推理过程来解答，又可以应用涉及一定难度的数学知识的快速推理过程来解答。最终目的是对评估结果错误/正确的二分法的补充，了解了学生运用数学推理的能力。①

使用日志数据的另一个作用是衡量学生的修复力/坚毅，这两点品质对数学学习的成功至关重要。坚毅与数学学业成绩之间的关系如图5所示（见上页）

参考文献

文献来源：Sanjoy Mahajan，Zbigniew Marciniak，Bill Schmidt，

Charles Fadel PISA Mathematics in 2021：An analysis of the CENTER FOR CURRICULUM REDESIGN.2016.CCR。原文报告共45页。后20页是数学试题实例，根据作者建议未做翻译。

报告原文下载https：//curriculumredesign.org/wp-content/up-

loads/Recommendations-for-PISA-Maths-2021-FINAL-EXTENDED-VERSION-WITH-EXAMPLES-CCR.pdf.

（责任编辑 杜丹丹 王策）

PISA Mathematics in 2021

—An analysis of the CCR

Authors：Sanjoy Mahajan，Zbigniew Marciniak，Bill Schmidt，Charles Fadel

Translators：WANG Mingjun，SHENG Qunli

（1.Olin College of Engineering，America;

2.University of Warsaw，Poland;

3.Michigan State University，America;

4.Center for Curriculum Redesgin，America;

5.School of Education，Lishui University，Lishui，Zhejiang，China 323000;

6.School of Education，Zhejiang University，Hangzhou，Zhejiang，China 310028）

Abstract： Mathematics is a foundation for understanding the world，citizenship and economic growth.As the 21st century bears little resemblance to the 19th century，education curricula are overdue for emphasizing depth of understanding and versatility，to meet the needs of our global society.The PISA test on mathematics measures，among other things， students’ability to employ mathematical reasoning while solving problems.We suggest enriching the descriptions of the mathematical processes（formulate，employ，interpret，evaluate），identified in the PISA Mathematics Framework as the main components of the modeling cycle，with seven reasoning tools which are most commonly used in search of the right approach：formulating situations mathematically（comparison， proportional reasoning，applying multiplicative scales）;employing mathematical concepts，facts， procedures，and reasoning（divide and conquer，lumping，consider first easy cases，probabilistic and logical reasoning）;and interpreting，applying and evaluating mathematical outcomes. PISA Mathematics Literacy Areas involves Shape & Space，Change & Relationships，Uncertainty & Data and Quantity， also developing creativity in mathematical thinking and competencies（Skills，Character，Meta-Learning）.

Key words： mathematics literacy and competencies;PISA mathematics framework;reasoning tools; problem solving ability.