基于混合算法优化支持向量机的供热负荷预测模型

于晓娟　齐先硕　顾吉浩　齐承英　孙春华

摘要 支持向量机回归（Support Vector Machine Regression，SVR）作为供热预测领域的一种新型算法，普适性强，但预测精度在一定程度上受参数选择的影响。为提高预测精度，提出一种基于差分进化（Differential Evolution，DE）和灰狼优化（Grey Wolf Optimization，GWO）的混合算法（DE-GWO）对支持向量机的回归参数进行寻优。该算法首先利用DE的变异、选择维持种群的多样性，然后利用GWO的全局寻优能力搜索SVR的最优参数组合，并采用均方误差（MSE）、平均绝对百分比误差（MAPE）、平均绝对误差（MAE）和判定系数（R2）对各种预测模型进行了评价。研究结果表明，DE-GWO-SVR预测模型的MAPE值为3.23%，优于SVR、DE-SVR、GWO-SVR模型，可为实际应用提供一定的参考。

关 键 词 热负荷预测;支持向量机;差分进化;灰狼优化;混合算法

中图分类号 TU833     文献标志码 A

Heat load prediction model based on support vector machine opti-mized by hybrid algorithm

YU Xiaojuan1， QI Xianshuo2， GU Jihao1， QI Chengying1， SUN Chunhua1

（1. School of Energy and Environmental Engineering， Hebei University of Technology，  Tianjin 300401， China; 2. College of Mathematics and System Science， Shandong University of Science and Technology， Qingdao， Shandong 266590， China）

Abstract As a new algorithm， support vector machine regression （SVR） has an obvious advantage in heat load prediction. However，  the prediction accuracy of SVR is generally influenced by parameters selection. In order to improve the prediction accuracy， a hybrid algorithm based on differential evolution and grey wolf optimization is proposed to optimize regression parameters of SVR. In this paper， the hybrid algorithm based on mutation and selection was used to maintain the diversity of the population. Then， the global optimization ability of GWO was adopted to get the optimal parameters of SVR.  In  addition， mean square error （MSE）， mean absolute percentage error （MAPE）， mean absolute error （MAE） and coefficient of determination （R2） were used to evaluate those forecasting models， respectively. The results show that the MAPE of DE-GWO-SVR model was 3.23%， and the accuracy of DE-GWO-SVR was the highest compared with the SVR， DE-SVR and GWO-SVR. Therefore， this hybrid algorithm can be recommended to guide the engineering application.

Key words heat   load  prediction;  support  vector  machine;  differential  evolution;  grey  wolf  optimization;  hybrid algorithm

0 引言

我國建筑能耗占总能耗的40%，其中供热、制冷能耗占建筑能耗的68%[1]。目前，我国城市和工业园区供热已基本形成“以燃煤热电联产和大型锅炉房集中供热为主、分散燃煤锅炉和其他清洁能源供热为辅”的供热格局。随着城市和工业园区经济的发展，供热需求不断增加，但由于许多地区发展规划过于超前，热电布局与城市发展不相符、不协调，缺乏科学合理的热负荷预测，热电联产集中供热的能源综合利用效率较低。因此，进行及时准确的热负荷预测，对于建设规划科学、布局合理、利用高效、供热安全的新一代热电联产产业格局尤为重要。

传统的负荷预测方法主要有回归分析法、时间序列法、神经网络法等[2]。Park等[3]运用多元线性回归（Multiple Linear Regression，MLR）和人工神经网络模型（Artificial Neural Network，ANN）进行了大型地源热泵系统的供热性能分析和预测，MLR和ANN的根均方根误差变异系数分别为3.56%、1.75%。Fang等[4]提出一种结合线性回归的季节性差分自回归滑动平均模型，综合考虑用户的行为习惯对冷热负荷的影响，对未来168 h的负荷进行了预测，MAPE值为5.58%。孙育英等[5]以海南三亚2座五星级宾馆的空调运行负荷实测数据为基础，利用广义回归神经网络建立了混沌预测模型，对未来1 h预测结果的期望偏差百分数分别为6.1%和8.2%。Xie[6]将BP神经网络预测理论与马尔科夫预测方法相结合对未来10 d进行了热负荷预测，预测结果的相对误差均低于0.002。刘倩颖等[7]将Kmeans聚类与BP相结合预测办公建筑日用电负荷，预测相对误差的绝对值控制在2.5%以内。Jovanović等[8]将多种神经网络组合预测供热负荷，研究表明预测精度优于单一的神经网络。

支持向量机是90年代中期发展起来的一种新型监督式学习预测方法，该方法基于结构化风险理论，相对于神经网络，拥有可靠的统计理论基础，实现了全局寻优，且对于高维度、小样本数据有较高的预测精度，在负荷预测技术领域频繁使用。刘庆典等[9]提出一种基于混沌相空间重构和支持向量机的短期空调负荷预测方法，仿真结果表明，混沌支持向量机方法的预测精度比单一支持向量机法预测结果期望误差百分比降低了31.4%，预测精度有了明显提升。Idowu等[10]以室外温度、热负荷历史数据等为输入变量，采用支持向量机回归、回归树、前馈神经网络和多元线性回归模型进行了热负荷预测，其中支持向量机回归精度最优，均方根误差为0.07。

支持向量机预测结果的精度与其参数的选择密切相关。Mirjalili等[11]于2014年提出一种新的基于种群的灰狼优化算法，近年来，在各个领域广泛应用。Jayakumar等[12]应用灰狼优化算法进行了热电联合调度的优化，实现了成本和排放的折中方案。Shakarami等[13]提出一种基于灰狼优化算法的广域电力系统稳定器的设计方法，并在小型和大型电力系统验证了该方法的有效性。Wang等[14]运用基于灰狼优化的核极限学习机算法进行破产预测，并分别与粒子群、遗传算法、网格搜索进行对比，结果表明灰狼优化预测模型具有优异的破产预测性能。Kohli等[15]提出一种混沌灰狼优化算法来解决约束优化问题，并采用了5种工程设计约束问题验证了该算法的优越性。Gupta等[16]运用一种新的随机漫步灰狼优化算法提升灰狼的搜寻能力，运用2014国际进化计算会议的30个基准问题来验证该算法的鲁棒性，证明了该算法针对连续目标优化和现实生活优化问题中的有效性和可靠性。Bian等[17]提出一种基于灰狼优化的支持向量机算法进行超临界二氧化碳中溶质溶解度的关联预测，并与27种常用经验模型对比表明，所提出的模型总体平均绝对相对偏差最低（3.20%）。

综上，本文提出一种基于差分进化和灰狼优化的混合算法对支持向量回归机参数寻优，对某住宅建筑进行供热负荷预测，以下统称DE-GWO-SVR，以提高单一支持向量机预测方法的精度，该供热负荷预测的方法同样适用于换热站和热源。

1 支持向量机回归

支持向量机回归（Support Vector Machine Regression， SVR）基本原理主要是通过适当的非线性变换将输入变量映射到1个高维特征空间，并在该空间寻找线性回归最优超平面归结为凸规划问题，求取全局最优解。数学描述如下

[max     -12i，j=1nα*i-αiα*j-αjKxi，xj+i=1nα*iyi-ε-i=1nαiyi-ε] ， （1）

[s.t.  i=1nαi=i=1nα*i0≤αi，α*i≤C   i=1，2，…，n]  。 （2）

式中：[αi，α*i，αj，α*j]为Lagrange乘子;[yi]为观测值;C为误差惩罚参数，C>0;ε为误差上限;[Kxi，xj]为核函数。

文献[18]给出了具有良好非线性能力且处理多输入变量具有自适应性的径向基内积函数[Kxi，x=exp（-xi-xj22σ2）=exp（-gxi-xj2）]，本文选用该函数作为SVR核函数。

综上，SVR计算过程中主要涉及2个影响参数，即惩罚参数C和核函数参数g。SVR参数的选择对模型的预测精度有很大影响，参数选择不当易出现过学习或欠学习现象。因此，本文分别以差分进化、灰狼优化和基于差分进化和灰狼优化的混合算法对SVR的参数C和g进行优化。

2 优化算法

2.1 差分进化（Differential Evolution， DE）

DE是一种模拟生物进化的随机选择模型，基本操作包括变异、交叉和选择[19]。

2.1.1 变异

目标矢量[Xti]，变异个体由式（3）生成

[Pt+1i=Xtk1+F（Xtk2-Xtk3）]  ， （3）

式中：F为缩放因子，取值范围为[0，1];[Xtk1，Xtk2，Xtk3]为第t代群体中3个随机矢量[k1，k2，k3∈[1，2，…，NP]]，且[k1≠k2≠k3]。

2.1.2 交叉

目标矢量[Xti]与变异矢量[Pt+1i]进行交叉，产生试验个体[Ut+1ij]。交叉操作的方程为

[Ut+1ij=Pt+1ij，     rand（j）≤CR  or  j=rand n（i）Xtij，        rand（j）>CR  or  j≠rand n（i）]  ， （4）

式中：[rand（j）∈[0，1]]，為均匀分布的随机数，[j]为第[j]个变量;[randn（i）∈[1，2，…，D]]，为随机选中的维数变量索引;[CR]为交叉概率，[CR∈[0，1]]。

2.1.2 选择

变异与交叉操作生成的试验个体[Ut+1ij]与[Xti]竞争，选择适应度较优的作为子代。选择方程为

[Xt+1i=Ut+1i，     f（Ut+1i）<f（Xti）Xti，      f（Ut+1i）≥f（Xti）]   。 （5）

2.2 灰狼优化（Grey Wolf Optimization， GWO）

灰狼算法是通过模拟灰狼群体等级制度和捕食行为而提出的新型启发式算法。该算法具有结构简单、收敛迅速、可调参数少等优点。

随机产生一群灰狼，定义优化目标函数为适应度函数，将适应度值最优、第2、第3的解定为[α，β，δ]，剩余候选解为[w]。[α，β，δ]狼最接近猎物，依靠[α，β，δ]狼估计猎物的位置，[w]通过计算自身与[α，β，δ]狼的距离来更新自身位置，并跟随[α，β，δ]进行搜素、追踪和包围猎物，其中猎物的位置即所求最优解。

假设搜索空间为d维，[xi=（xi1，xi2，…，xid）]，表示第[i]只狼的位置，灰狼包围猎物的公式为

[d=c∙xtp-xt]，[c=2r1]。 （6）

灰狼位置更新为

[xt+1=xtp-bd]，[b=2ar2-a]， （7）

式中：[xt]为第[t]次迭代灰狼的位置;[xtp]第[t]次迭代猎物的位置;[c]为摇摆因子;[r1∈[0，1]];[b]为收敛因子;[r2∈[0，1]];[a]随迭代次数的增加从2线性递减为0。

[w]狼计算自身与[α，β，δ]狼的距离公式为

[dα=c1∙xtα-xt]，[dβ=c2∙xtβ-xt]，[dδ=c3∙xtδ-xt]。 （8）

[w]狼更新自身位置公式为

[xt+11=xtα-b1∙dα]，[xt+12=xtβ-b2∙dβ]，[xt+13=xtδ-b3∙dδ]。 （9）

猎物所在位置为

[xt+1=xt+11+xt+12+xt+133]  。 （10）

2.3 混合算法（DE-GWO）

DE-GWO为结合DE与GWO算法的一种全新的优化方法，该方法首先利用DE算法变异、选择保持种群的多样性，再将其作为GWO初始种群找出适应度值最优的[xα，xβ，xδ]，最后利用DE的交叉、选择更新灰狼位置，重复上述过程，直至选出最优目标函数值。

3 研究对象

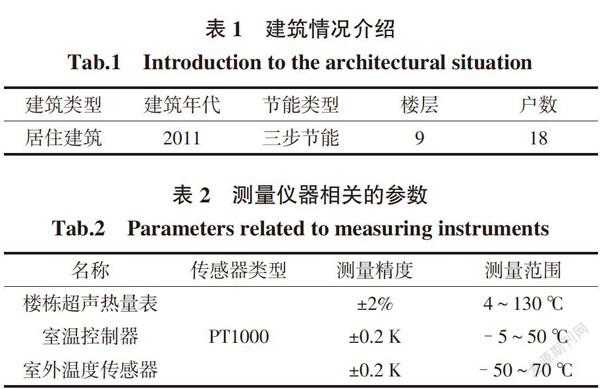
本文以石家庄市某栋居住建筑为研究对象，该建筑在2013年采用通断时间面积法进行了供热计量改造，建筑类型等情况详见表1。

选取该楼栋2016年11月15日至2017年3月14日的采暖数据为样本，样本数据共计17 280组。采集参数主要包括楼栋和用户的供/回水温度、楼栋的供/回水压力、室内温度、室外温度、楼栋的累计流量、楼栋和用户的累计热量等。测量仪器相关参数如表2所示。其中，室外温度、室内温度的采集频率均为1次/10 min，楼栋热量表的采集频率为1次/2 h。由于数据采集的周期比较长，易出现异常数据，且异常数据会对预测模型产生较大影响，因此本文采用多项式拟合和插值方法进行了修正。

Jie等[20]对供热负荷的影响因素进行了评价，其中室外温度是影响热负荷的最重要因素。张佼等[21]将预测日前3天的历史日累计耗热量输入预测模型，预测结果的平均绝对百分比误差为4.33%。室内温度作为热负荷的影响因素，以往难以获得长期的监测数据。文中居住建筑经节能改造后，室内温控器可对各个用户的室温进行定期采集。结合实测数据以及供热计量的特性，本文考虑采用室内日平均温度[tn]、室外日平均温度[tw]和历史日累计耗热量作为预测模型的输入变量，供热负荷预测模型的表达式为

[Qt=f（tn，tw，Qt-1，Qt-2，Qt-3）]  。 （11）

该研究对象中的所有用户均安装了室温控制器，且统一安装于内墙的统一高度（1.5 m左右）。日均室内温度的计算方法为

[tjn=1Ni=1N（1KTin，j）]   ， （12）

式中：[tjn]为该栋第[j]天的室内日均温;N为末端热用户数;[Tin，j]为用户[i]在第[j]天的室内温度实時值;K为日采集次数。

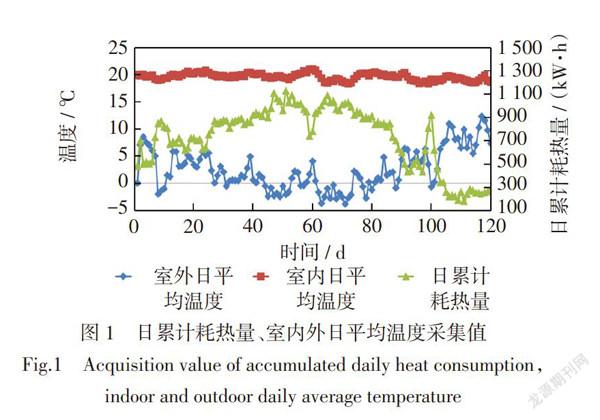
图1为整个采暖季（120 d）供热数据输入变量的实际采集值。

由于目前可以获取未来7 d的气象参数，因此作者考虑对未来7 d的供热负荷进行预测。综上，本文分别采用SVR、DE-SVR、GWO-SVR和DE-GWO-SVR对采暖季前113 d的数据进行训练，采用采暖季后7 d的数据对预测结果进行检验。

4 仿真建模

4.1 模型评价

本文选取平均绝对百分比误差（MAPE），平均绝对误差（MAE）、均方误差（MSE）和判定系数R2作为模型效果测试的评价指标，各指标具体表达式为

[MAPE=1Nt=1NQt-QtQt×]100%， （13）

[MAE=1Ni=1NQt-Qt]   ， （14）

[MSE=1Nt=1N（Qt-Qt）2]  ， （15）

[R2=[Ni=1NQ∙Qt-i=1NQi=1NQt]2Ni=1NQ2-[Ni=1NQ]2[Ni=1NQt2-（i=1NQt）2]] ， （16）

式中：[Qt]为预测值;[Qt]为实际值;N为预测的天数。MAPE、MAE、MSE越小，R2越接近1，则预测精度越高。

4.2 DE-SVR

设置种群规模为20，迭代次数为100，缩放因子下界为0.2，缩放因子上界为0.8，交叉概率为0.2。在该参数下根据公式（3）～（5）进行变异、交叉、选择操作，选出适应度最优的个体。

4.3 GWO-SVR

初始参数设置同DE-SVR。在该参数下初始化[α，β，δ]狼的位置，由式（10）～（11）计算出其他灰狼个体与[α，β，δ]的距离及灰狼的位置更新，由式（12）确定猎物所在的位置，即最优解。

4.4 DE-GWO-SVR

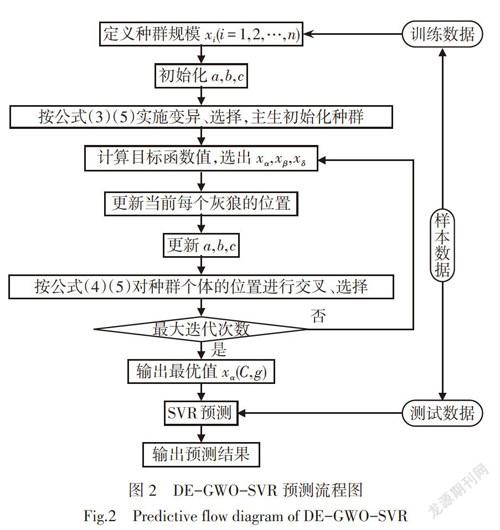
采用DE和GWO混合算法的预测流程图如图2所示。

DE-GWO-SVR模型具体实施步骤如下：

1）参数设置初始化，设置方法用DE-SVR;

2）根据式（3）、（5）实施DE变异、选择，生成初始种群;

3）根据式（6）～（9）计算其他灰狼与最优个体距离，并进行位置更新;

4）根据式（4）、（5）实施DE交叉、选择新的个体;

5）计算适应度值，并与原来的适应度值进行比较，保留最优解，并更新最优的3个灰狼[xα，xβ，xδ]位置;

6）重复迭代，判断是否达到最大迭代次数，若达到，输出全局最优解[xα]的目标函数值;

7）将该位置坐标作为SVR预测参数输入SVR模型，进行预测。

5 结果与讨论

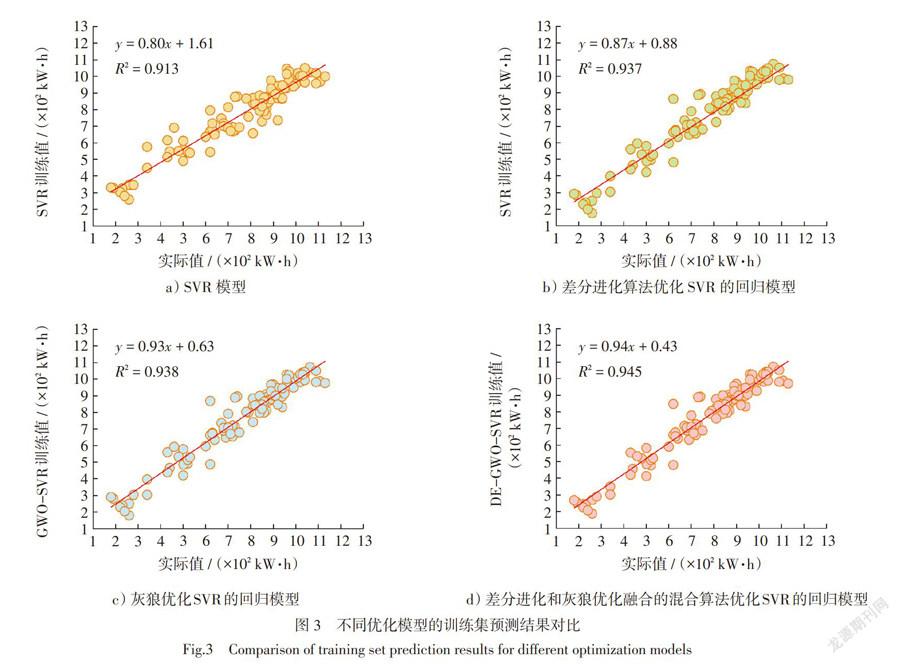
以该楼栋整个采暖季运行数据为基础，利用2016年11月15日至2017年3月7日的数据构建样本，进行了仿真建模。SVR、DE-SVR、GWO-SVR、DE-GWO-SVR预测模型的训练集建模结果对比如图3所示。

图3a）为SVR模型训练集的实际值与预测值对比结果。判定系数R2表示因变量的变异中可由所选自变量解释部分所占的比例。可以看出，判定系数R2=0.913，表明所选自变量能较好地解释因变量的变化。图3b）为差分进化算法优化SVR的回归结果对比，其中R2=0.937，相对于单一的SVR模型预测精度有所提高，主要是SVR模型参数的优化选择对于预测精度起到一定的提高作用。图3c）为灰狼优化SVR的回归模型的实际值与预测值对比。可以看出，该模型拟合精度与差分进化优化SVR模型精度相接近，且实际值与预测值间具有较高的拟合精度。图3d）为将差分进化和灰狼优化融合的混合算法优化SVR的回归结果对比。混合算法优化SVR预测模型后的实际值与预测值的判定系数R2=0.945，图形数据点在拟合曲线周围分布集中，表明实际值与预测值的线性依存能力很强，模型对因变量具有较高的解释能力。

综上，4种预测模型的回归结果都具有较高精度，其中DE-GWO-SVR预测模型判定系数R2均高于SVR、DE-SVR、GWO-SVR预测模型，具有更高的预测精度。

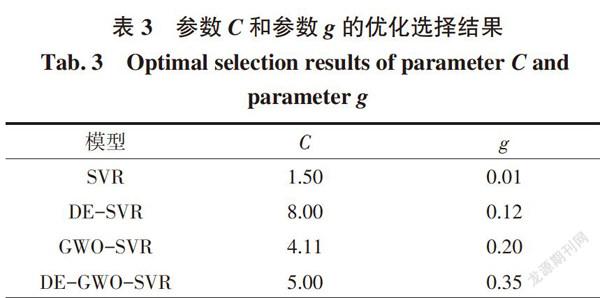
表3为参数C和参数g的优化选择结果，将最优参数对输入SVR模型并进行下一步预测。

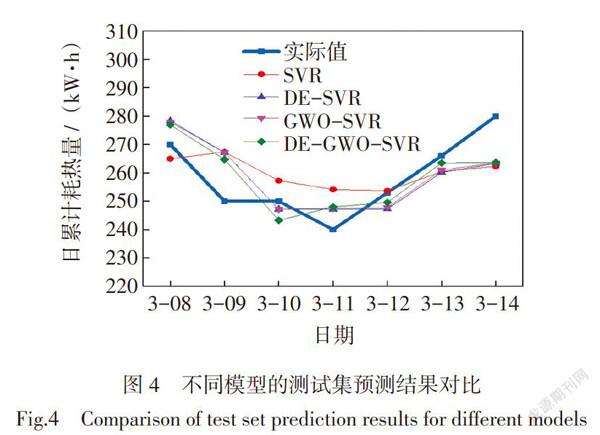
利用2017年3月8日至2017年3月14日的数据进行检验。基于上述的4种预测模型，分别将未来7天的自变量输入模型，得出热负荷预测值，将预测结果与实际采集的数据进行了对比，预测结果如图4和图5所示。

由图4可以看出，SVR、DE-SVR、GWO-SVR和DE-GWO-SVR均相对成功地预测了负荷的变化趋势，但SVR相对于其他优化模型的预测误差较大，进一步说明了参数优化对于预测结果的重要影响。

图5给出了不同模型测试集的预测结果误差对比情况。由上图可知，本文建立的4种预测模型相对误差的平均值在±3%左右，预测模型相对误差量最小值为0.8%，最大值为8%。其中，DE-GWO-SVR的相对误差平均值低于其他预测模型，预测精度更高，在实际中推荐使用。

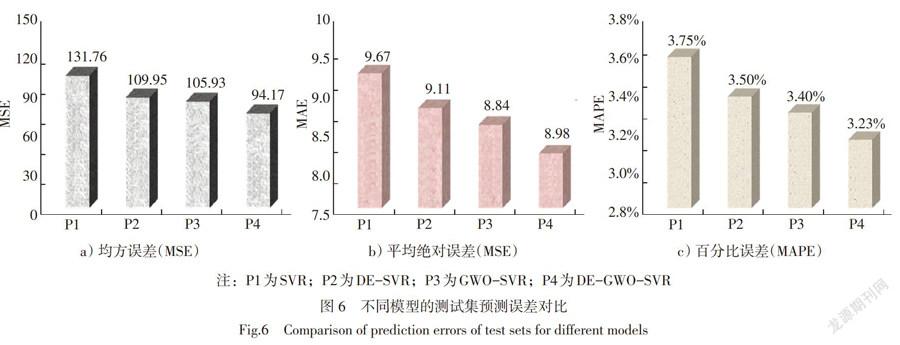
图6为不同预测模型测试集预测误差结果对比。由图6中可以看出，4种预测模型的MAPE值均低于4%的平均水平。其中，DE-SVR、GWO-SVR、DE-GWO-SVR预测模型的MSE、MAE、MAPE值均低于传统的SVR模型，说明了参数优化模型具有更好的预测精度。DE-GWO-SVR的MAPE值为3.23%，与SVR、DE-SVR和GWO-SVR相比，MAPE分别降低0.52%，0.27%和0.17%。DE-GWO-SVR的MSE值为94.17，与SVR、DE-SVR和GWO-SVR相比，MSE分别减少37.59、15.78和11.76。另外，SVR的MAE值最大，与DE-SVR、GWO-SVR和DE-GWO-SVR相比，MAE分别增加0.56、0.83和1.29。

綜上，DE-GWO-SVR模型证实了本文提出的混合优化算法的优越性，该算法较单一的差分进化、单一的灰狼优化具有更高的预测精度。

6 结论

1）分别采用差分进化、灰狼优化和基于差分进化和灰狼优化的混合算法对SVR的参数寻优选择，克服了传统SVR参数选择的随意性，为建立可靠的预测模型提供了良好的基础条件。

2）采用混合优化后的预测模型DE-GWO-SVR，对未来7天的供热负荷进行了预测，并与其他3种模型的预测精度进行了对比。结果表明，DE-GWO-SVR预测模型的最大相对误差为5.9%，MAPE值为3.23%，预测精度最高，可在供热企业的能源储备和生产调度应用中推荐使用。

参考文献：

[1]    DING Y，ZHANG Q，YUAN T H，et al. Model input selection for building heating load prediction：A case study for an office building in Tianjin [J]. Energy and Buildings，2018，159：254-270.

[2]    景胜蓝，王飞，雷勇刚. 热负荷预测方法研究综述[J]. 建筑热能通风空调，2015，34（4）：31-35.

[3]    PARK S K，MOON H J，MIN K C，et al. Application of a multiple linear regression and an artificial neural network model for the heating performance analysis and hourly prediction of a large-scale ground source heat pump system[J]. Energy and Buildings，2018，165：206-215.

[4]    FANG T T，LAHDELMA R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system[J]. Applied Energy，2016，179：544-552.

[5]    孫育英，王伟，朱佳鹤，等. 空调运行负荷的混沌特性分析及GRNN混沌预测方法研究[J]. 建筑科学，2014，30（10）：13-17，40.

[6]    XIE L. The heat load prediction model based on BP neural network-Markov model[J]. Procedia Computer Science，2017，107（Supplement C）：296-300.

[7]    刘倩颖，阮应君，时翔，等. 基于kmeans聚类与BP神经网络算法的办公建筑逐时电负荷预测[J]. 热能动力工程，2018，33（3）：138-144.

[8]    JOVANOVIĆ R Ž，SRETENOVIĆ A A，ŽIVKOVIĆ B D. Ensemble of various neural networks for prediction of heating energy consumption [J]. Energy and Buildings，2015，94：189-199.

[9]    刘庆典，周璇，凡祖兵，等. 基于混沌支持向量回归机的短期空调负荷预测[J]. 建筑科学，2016，32（6）：102-107.

[10]  IDOWU S，SAGUNA S，ÅHLUND C，et al. Applied machine learning：Forecasting heat load in district heating system[J]. Energy and Buildings，2016，133：478-488.

[11]  MIRJALILI S，MIRJALILI S M，Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software，2014，69：46-61.

[12]  JAYAKUMAR N，SUBRAMANIAN S，GANESAN S，et al. Grey wolf optimization for combined heat and power dispatch with cogeneration systems[J]. International Journal of Electrical Power & Energy Systems，2016，74：252-264.

[13]  SHAKARAMI M R，FARAJI DAVOUDKHANI I. Wide-area power system stabilizer design based on grey wolf optimization algorithm considering the time delay [J]. Electric Power Systems Research，2016，133：149-159.

[14]  WANG M J，CHEN H L，LI H Z，et al. Grey wolf optimization evolving kernel extreme learning machine：Application to bankruptcy prediction[J]. Engineering Applications of Artificial Intelligence，2017，63：54-68.

[15]  KOHLI M，ARORA S. Chaotic grey wolf optimization algorithm for constrained optimization problems[J]. Journal of Computational Design and Engineering，2018，5（4）：458-472.

[16]  GUPTA S，DEEP K. A novel random walk grey wolf optimizer[J]. Swarm and Evolutionary Computation，2019，44：101-112.

[17]  BIAN X Q，ZHANG Q，ZHANG L，et al. A grey wolf optimizer-based support vector machine for the solubility of aromatic compounds in supercritical carbon dioxide[J]. Chemical Engineering Research and Design，2017，123：284-294.

[18]  PROTI M，SHAMSHIRBAND S，PETKOVIĆ D，et al. Forecasting of consumers heat load in district heating systems using the support vector machine with a discrete wavelet transform algorithm[J]. Energy，2015，87：343-351.

[19]  刘振泽，许洋，王峰明. 改进差分进化算法在非线性模型预测控制中的应用[J]. 北京工业大学学报，2015，41（5）：680-685.

[20]  JIE P F，ZHU N，LI D Y. Operation optimization of existing district heating systems[J]. Applied Thermal Engineering，2015，78：278-288.

[21]  张佼，田琦，王美萍. 基于遗传算法优化支持向量回归机参数的供热负荷预测[J]. 暖通空调，2017，47（2）：104-108，25.

[责任编辑 田 丰]