中欧集装箱多式联运路径选择优化研究

万杰　魏爽　耿丽

摘要 在中欧集装箱多式联运现状研究的基础上，采用模糊等级评价法对港口城市和中欧班列城市的物流服务质量进行评价，综合考虑多式联运物流网络中物流成本以及物流服务质量，建立了多式联运路径优化数学模型，设计了求解多目标的遗传算法，为中国运输至欧洲的多式联运路径选择提供参考。

关 键 词 综合交通运输;路径选择优化;遗传算法;中欧集装箱运输;多式联运

中图分类号 U15     文献标志码 A

Research on the optimization of logistics routing in China-EU container intermodal transport

WAN Jie， WEI Shuang， GENG Li

（School of Economics and Management， Hebei University of Technology， Tianjin 300401， China）

Abstract Based on the current status of China-EU container multimodal transport， this paper uses fuzzy evaluation method to evaluate the logistics service quality of port cities and Central European cities， and considers the logistics costs and logistics service quality of multimodal transport logistics network. The mathematical model of intermodal route optimization was designed and a multi-objective genetic algorithm was designed to provide a reference for the multimodal transport selection from China to Europe.

Key words integrated transportation; path selection optimization; genetic algorithm; China-EU container transport; multimodal transport

過去的一个多世纪以来，由于海运技术的不断发展及其运输成本的优势，中欧贸易集装箱运输主要是通过海上通道来完成，随着“一带一路”的提出，在国内各地政府对开行中欧班列的大力推进下，中欧班列货物分担率在不断提高。目前关于中欧集装箱运输的研究主要为中欧班列集装箱运输公司选择的研究[1]、中欧班列开行方案的研究[2]、中欧航线集装箱运价的研究[3]以及中欧集装箱多式联运的研究。对于多式联运物流路径选择的研究主要集中在不同的因素而模型构建和算法优化。多式联运物流路径选择受运输费用、运输时间、服务质量、运输风险、技术水平、环境因素以及行程利用率等因素的影响[4]，例如Cho等[5]选取成本和时间为目标，应用从釜山到鹿特丹的实际运输路线来验证标签算法;Seo等[6]选取运输费用、运输时间以及信心指数研究重庆到荷兰鹿特丹的笔记本电脑出口多式联运路线选择问题;付新平等[7]选取运输时间和运输费用，研究从武汉到欧洲的国际集装箱多式联运线路问题;李玉民等[8]选取运输时间、运输费用和碳排放，构建中多式联运路径优化的多目标优化模型。目前对于物流服务质量的概念界定和构成要素还没有统一的见解，最广泛使用的是以时间、地点、效率、仓储为基础的物流服务质量。如Limbourg 等[9]设计了SERVQ UAL量表，将物流服务质量划分为4个维度，用越南岘港市的200家物流客户进行实证研究;郑茜[10]将运输时效性作为物流服务质量指标，构建多式联运优化模型。对于多式联运路径选择优化研究的求解算法多为启发式算法，其中包括蚁群算法[11]、遗传算法[12-13]、模拟退火算法[14]和声搜索算法[15]等。

前期对于该问题的研究多集中在多式联运运输费用方面，对于多式联运物流服务质量的研究较少，同时考虑到前期的研究多集中在国内领域，缺少基于现状的国际多式联运研究。综上所述，本文从中欧集装箱运输现状出发，分析了中欧班列开设城市节点以及主要港口城市物流服务质量影响因素，构建指标体系;抽象出物流网络模型，建立了综合考虑运输费用和物流服务质量的多目标优化模型，并设计求解该模型的遗传算法，能够较好的为中欧集装箱多式联运路径优化提供方案。

1 数学模型构建

1.1 问题描述

假设货物需要从出发点O运送至目的地D，途中可选择n个城市节点中的若干个作为中转，构建从出发点到目的点的完整路径。货物可由中欧班列开设城市节点B通过阿拉山口（霍尔果斯）、二连浩特或者满洲里（绥芬河）出境到达目的地;还可以由沿海港口城市C运输至国外港口D再到达目的地，任意相连的两个节点之间有公路、铁路和水运3种运输方式可供选择。除起点和终点外每个节点都可实现货物在不同运输方式之间的相互转载，客户对货物的运输时间有合理的区间要求。本文选取运输费用以及物流服务为主要因素来选择整个运输过程中所途经的节点及节点间最佳的运输方式和运输路径组合。多式联运网络结构如图1所示。

1.2 路径选择需考虑的因素

1）运输费用：中欧集装箱多式联运运输成本即在运输过程中所产生的费用成本函数，主要包括节点与节点之间的运输成本，节点上的换装成本，以及货物因没有准时到达而产生的惩罚成本。

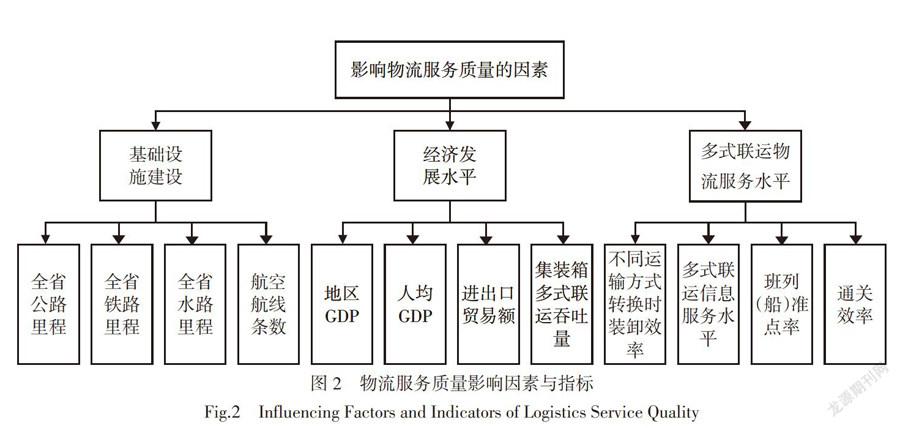
2）物流服務质量：中欧集装箱多式联运选择不同的运输路线会导致不同的服务质量。各城市节点依据自身资源（如基础设施建设、经济条件和运输组织资源等）与各种能力（如安全性、可靠性以及便利性等）为货物提供物流服务，对于不同的城市节点来说，自身资源和能力越好，所提供的物流服务质量越好。因此，综合港口城市和开设中欧班列的城市状况与特点，选取基础设施建设水平、经济发展水平以及多式联运物流服务水平来对城市节点进行分析。影响因素与指标如图2所示。采用模糊等级评价法[16]对各指标进行比较，根据不同指标的数字特征对建立评价准则集合{好，一般，差}，其对应的分值为{0.9，0.6，0.3}。

1.3 假设条件

1）货物的转载只能发生在城市节点，且在城市节点只能转载一次;

2）货物在运输途中不能分割;

3）货物在城市节点之间只能选择一种运输方式;

4）运输成本与运输距离和所选路线的单位运输成本成正比。

1.4 符号说明与模型建立

决策变量：[xmij]为0或1变量，当节点ij之间使用运输方式m时为1，否则为0;[ymli]为0或1变量，当在节点i由运输方式m转为l时为1，否则为0;[xi]为0或1变量，当货物通过城市节点i时为1否则为0。其他符号说明见表1。

多目标多式联运问题的混合整数规划模型如下

目标函数（1）式为最小化物流成本，包括运输成本、换装成本以及惩罚成本;目标函数（2）为最大化物流服务质量;约束条件（3）表示城市i、j之间只能选择一种运输方式;约束条件（4）表示城市节在节点i处只能转运一次;约束条件（5）表示该路径为一条完整路径;约束条件（6）表示惩罚函数;约束条件（7）表示决策变量取值为0或者1。

2 求解多式联运问题的遗传算法设计

2.1 遗传算法

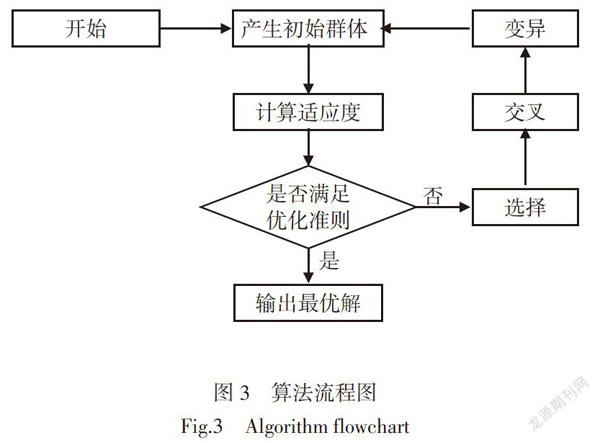
本文使用遗传算法进行求解。遗传算法是一种模拟自然界物种进化的过程、使用优胜劣汰的原则的启发式算法，遗传算法具有全局搜索能力，搜索过程简单易理解的特点。遗传算法流程如图3所示。

2.2 求解步骤

1）目标函数分析：因本文两个目标函数之间存在相互约束的关系，理想解为成本的最小值和物流服务质量的最大值。所以应将多目标转化为单目标优化

[minZ=mini=1nθiZi]， （8）

式中：[θi]为目标函数[Zi]所对应的权重，且[i=1nθi=1]，对应每组权重系数会有一个的pareto解。

2）编码：对节点城市和运输方式进行采用二进制编码，具体编码方式见图4。每一条染色体被分为两个部分：在城市节点部分，0、1变量表示是否通过该城市节点，在运输方式部分，0、1、2、3表示铁路、公路、水路和航运四种运输方式。

3）适应度值评价：由于目标函数单位不一致，需要通过统一量纲规范化各目标函数

[Z′i=Zi-min（Zi）max（Zi）-min（Zi）]， （9）

式中：[Zi]（ i = 1，2，…，m）表示目标函数;[Zi，max]表示目标函数的最大值;[Zi，min]表示目标函数的最小值。则适应度函数为

[fit（i）=1θ1Z′1+θ2Z′2+…+θiZ′i]。 （10）

4）选择：为了能将更好的信息传递给下一代同时保证种群的多样性，本文使用轮盘赌选择法进行操作。

5）交叉：为了防止当前群体的最优个体在下一代发生丢失，导致遗传算法不能收敛到全局最优解，本文采用单点交叉方式。选择的父辈个体通过交换部分信息，从而产生新的运输方案。

6）变异：本文中采用单点变异方法。在随机选取的个体中上按一定的概率改变基因，从而会产生新的运输路线。

7）算法终止：算法迭代到最大代数时终止。

3 算例分析

目前，已经开通的中欧班列运行线路分别是从阿拉山口（霍尔果斯）出境的西通道、二连浩特出境的中通道以及满洲里（绥芬河）出境的东通道。根据《中国口岸统计年鉴2017》整理铁路口岸运行情况来看，满洲里、二连浩特、绥芬河及阿拉山口（霍尔果斯）为铁路运输的4大铁路口岸，分别占到全国的32.4%、22.6%、20.7%、15.2%。因此，本算例选取满洲里、二连浩特、绥芬河及阿拉山口（霍尔果斯）为内陆口岸节点。选取天津、上海、大连、青岛、深圳、广州、厦门、宁波以及连云港9个沿海港口（中欧集装箱运输主要港口），共涉及23个城市节点，考虑到中国连续两年成为德国第一大贸易伙伴，双边贸易额高达1866亿美元，中国是德国第3大出口目的国和第1大进口来源国。并且中德贸易占中欧 （盟） 贸易量超过 30%，所以本文选取柏林为运输终点，海运运输口岸为鹿特丹港，由鹿特丹运往柏林选取铁路运输。

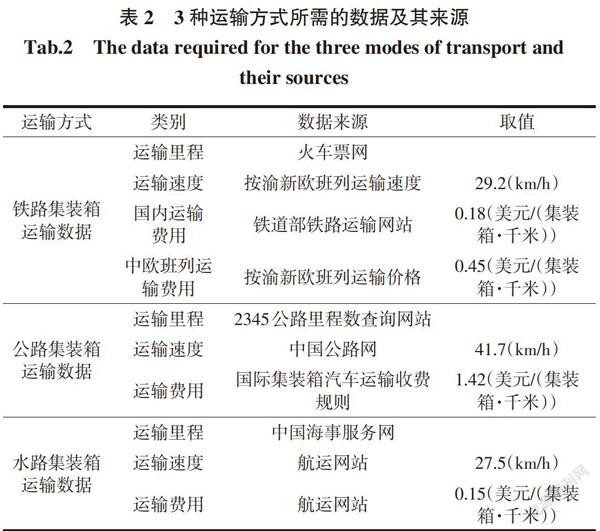
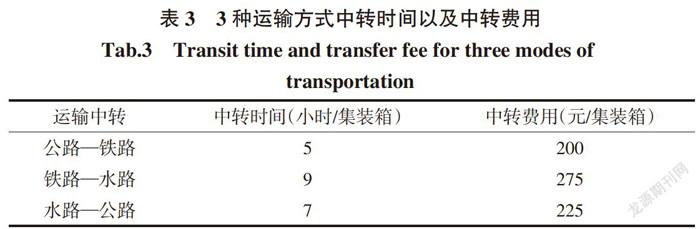
本算例中3种运输方式所需的数据及其来源如表2所示。运输方式之间的转换时间以及转换费用参照天津港口的收费标准，数据详见表3。中欧班列的在场平均箱等待时间由其一周之内开通的班列次数推算得出，港口枢纽城市节点的在场平均箱停留时间根据《中国港口年鉴2017》整理出;采用模糊等级评价法对16个城市节点进行综合比较，权重依据相关论文确定为0.2、0.2和0.6。计算出16个节点物流服务质量如表4所示。

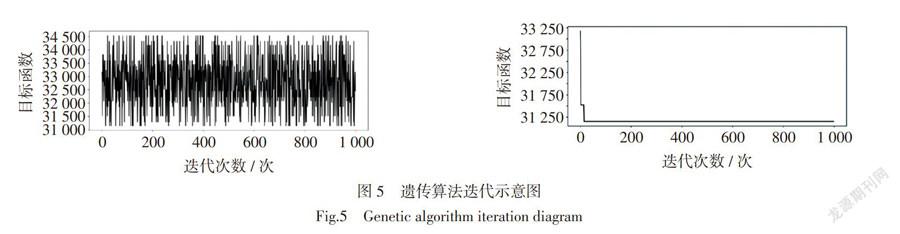
采用MATLAB对本文进行数学模型进行求解，遗传算法最大迭代次数设置为1 000次，交叉概率为0.8，变异概率为0.01。遗传算法迭代如图5所示，加权目标函数值为31 302.83，遗传算法迭代20次取得最优解。输出路线为西安→郑州（铁路）→深圳（铁路）→鹿特丹（水路）→柏林（铁路）。

4 总结

本文从中欧集装箱运输现状出发，分析了中欧班列开设城市节点以及主要港口城市物流服务质量影响因素，构建指标体系;抽象出物流网络模型，建立了综合考虑运输费用和物流服务质量的多目标优化模型，模型理论清晰，考虑了现实情况，符合实际。采用遗传算法进行求解，以“西安—柏林”集装箱运输进行算例分析，结果表明，该模型和算法能够有效地为中欧集装箱多式联运路径选择提供方案和路线参考。

今后可以增加更多的城市节点进行深入研究，对运算结果进行分析，讨论当前物流网络结构是否合理;还可以对算法进一步研究，提出解决多式联运问题的新算法。

参考文献：

[1]    刘宗清. “一带一路”下中欧班列铁路运输公司选择研究[D]. 北京：北京交通大学，2017.

[2]    韩雪. 中欧班列开行方案研究[D]. 北京：北京交通大学，2017.

[3]    余国英. 中欧贸易航线集装箱班轮运价研究[D]. 青岛：中国海洋大学，2011.

[4]    伍转青. 物流企业多式联运运输线路选择研究[J]. 铁路采购与物流，2011，6（2）： 52-54.

[5]    CHO J H，KIM H S，CHOI H R. An intermodal transport network planning algorithm using dynamic programming：A case study：from Busan to Rotterdam in intermodal freight routing[J]. Applied Intelligence，2012，36（3）： 529-541.

[6]    SEO Y J，CHEN F，ROH S Y. Multimodal transportation：the case of laptop from Chongqing in China to rotterdam in Europe[J]. The Asian Journal of Shipping and Logistics，2017，33（3）： 155-165.

[7]    付新平，何瑜莎，鄒敏，等. 国际集装箱多式联运线路选择研究[J]. 铁道运输与经济，2017，39（12）：12-17

[8]    李玉民，郭晓燕，杨露，等. 考虑多目标的中欧集装箱多式联运路径选择[J]. 铁道科学与工程学报，2017，14（10）：2239-2248.

[9]    LIMBOURG S，GIANG H T Q. Cools M. Logistics service quality：the case of Da Nang city [J]. Procedia Engineering，2016，142：124-130.

[10]  郑茜. 低碳约束下多式联运路径优化问题研究[D]. 杭州：浙江工商大学，2017.

[11]  刘维林. 基于动态蚁群算法的集装箱国际多式联运路径优化研究[J]. 北京交通大学学报（社会科学版），2012（3）：57-62.

[12]  何狄江. 遗传算法在多式联运路径优化的应用[D]. 杭州：杭州电子科技大学，2017.

[13]  张润杰. 基于改进遗传算法的多式联运路径优化研究[J]. 物流工程与管理，2014，36（5）：95-96，88.

[14]  郭丹丹. 基于模拟退火混合遗传算法的多式联运优化问题的研究[D]. 大连：大连海事大学，2012.

[15]  赖志柱. 和声搜索算法优化多时间窗多式联运运输方案[J]. 计算机应用，2013，33（9）：2640-2642，2693.

[16]  付新平，张雪，邹敏，等. 基于价值量模型的中欧班列经济性比较分析[J]. 铁道运输与经济，2016，38（11）：1-5.

[责任编辑 田 丰]